基于2.5维有限元法的有限长波导结构模态密度计算
2022-03-18张淑敏圣小珍杨世均
张淑敏, 圣小珍, 杨世均
(1.山东职业学院 铁道学院,济南 250104;2.上海工程技术大学 城市轨道交通学院,上海 201620;3.西南交通大学 牵引动力国家重点实验室,成都 610031)
统计能量分析(statistical energy analysis,SEA)方法[1-2]作为研究复杂系统高频动态声振响应的一种重要方法,已广泛应用于飞机、轮船、高速列车等行业。模态密度作为统计能量分析子系统的主要参数之一,定义为单位频率下结构的模态数,能够表征结构对外界宽频激励产生共振响应的能力。模态密度越大,结构越容易从宽带激励中吸收能量。文献[3]表明,子系统模态密度的精度对SEA模型的预测结果有较大影响。
简单子系统(如杆、梁、板、圆柱壳等)的模态密度可通过系统的频率方程进行求解。Lyon等指出,当频率较高时,子系统的模态密度与边界条件无关。Xie等[4]基于波数积分法和相位闭合原理研究了边界条件对一维和二维结构模态密度的影响。对曲板、三明治板、蜂窝板等结构的模态密度获取,Langley等[5-8]分别给出了详细的推导过程和计算公式。
不同于简单结构的模态密度,复杂结构的模态密度一般通过试验测试获取。根据测试手段的不同,可将其分为模态计数法和点导纳法[9-10]。模态计数法是对结构导纳的峰值进行计数,相对比较简单,但由于复杂结构在高频区域的模态重叠数较大,因此该方法对高频不再适用[11]。点导纳法是基于结构激励点导纳实部的平均值(对测点进行平均)来计算模态密度,但该方法容易受到诸如激励形式,传感器附加质量等因素的影响,需进行一定的修正或者改进[12-14]。
此外,工程中还存在很多典型结构,如周期性结构和波导结构等,获取这类结构的模态密度时,可从波动角度进行考虑。针对周期性结构,Langley[15]通过与传播波相关联的相位常数推导了一维和二维结构的模态密度一般表达式;Cotoni等[16]综合应用周期结构理论、有限元法、和部件模态综合法(CMS)给出了周期性结构的模态密度表达式。
波导结构的主要特点是它在长度(x)方向上不论是材质还是几何形状都是均匀的,但横截面的形状可以是任意的。这种结构可以允许特定的结构波(特征波)在长度方向上自由传播。Aalami[17]研究波在任意截面杆中的传播特性时提出了2.5维有限元法(波数有限元法),随后该方法被广泛应用于钢轨[18]、复合板[19]、型材[20]等结构上。Renno等[21-22]利用2.5维有限元法计算了波导结构的受迫响应。Finnvede[23]利用2.5维有限元法推导了波导结构的群速度和模态密度的表达式,以组合梁结构和风洞结构为例,计算了结构的模态密度。
本文在文献[23]的基础上,以单板和高速列车铝型材为例,利用2.5维有限元法计算了结构的群速度和模态密度,通过提出波形置信度的概念,对波导结构频散曲线的特征波进行了分类,计算了不同特征波的群速度和模态密度。以薄板为例,从2.5维有限元法的模态密度公式出发,推导得到了经典薄板的模态密度理论公式,验证了利用2.5维有限元法计算有限长波导结构模态密度的合理性。
1 无限长波导结构特征波的频散方程
沿x方向无限长的波导结构如图1所示,那么结构的自由振动微分方程一般可表示为[24]
(1)
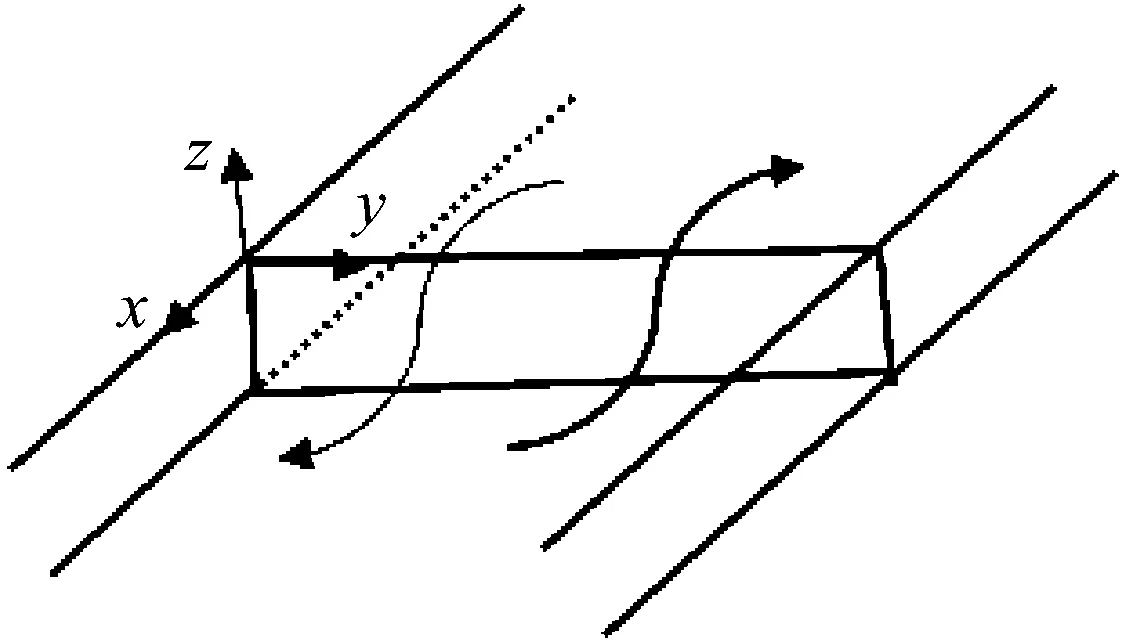
图1 沿x方向的无限长波导结构,其中曲线箭头表示沿+x和-x传播的振动波
式中:M和K2为3n×3n正定对称矩阵;K0为3n×3n对称非负矩阵;K1为3n×3n反对称矩阵。
假设结构在x方向存在波数为β,频率为ω的简谐波(即在空间和时间上均是简谐的振动波),即假定上述微分方程存在如下形式的解
(2)
将式(2)代入式(1),可得
(3)
det[-ω2M+K0+iβK1+β2K2]=0
(4)
2 无限长波导结构频散曲线和群速度
2.1 特征波频散曲线的分类
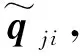
(5)
WAC矩阵的各元素代表两个波形之间的相关程度,其值位于[0,1]之间,越接近于1,说明两种波的波形越相似,可定义为同一类型的波。


2.2 波导结构特征波群速度的一般表达式
为求解无限长波导结构内特征波的群速度,对式(5)两边关于波数求导,得:
(6)
(7)
由于矩阵A=-ω2M+K0+iβK1+β2K2为Hermit矩阵,则由式(5)可得
(8)
此时,式(7)可写为
(9)
进一步得到结构的群速度为
(10)
特别地,第m条频散曲线(其与频率的关系记为gj(ω))对应的群速度为
ω≥ωj0
(11)
3 有限长波导结构的模态密度
3.1 结构总的模态密度
对于长度为L的杆、轴或梁结构,其振动模态可以看成是该结构为无限长时的两个特征波的干涉结果。这两个特征波幅值相同,相位满足特定关系,沿相反方向传播。高频时第j个特征波的波数βj与相应的模态阶数Nj近似满足如下关系
(12)
那么频带[ω1,ω2]间的平均模态密度可近似表示为
(13)
其中,Ntot(ω)可根据下式计算
(14)
而βj(ω)通过频散方程得到。
需要说明的是,该公式在频率ω1和ω2处的模态密度变化平稳时成立,如果频率ω1和ω2恰好位于结构截止频率附近,那么模态密度的计算可参考3.2节。
通过式(13)可以看出,结构总的模态密度可以通过求解特定频率下总的模态数得到,而SEA模型大多数是在三分之一倍频程内进行计算,因此只需对三分之一倍频程的上下频率进行模态数的计算即可。
3.2 结构特征波的模态密度
建立SEA预测模型的首要工作是对子系统进行合理的划分,振型相似准则是划分SEA子系统的准则之一,即将结构的一群具有相似共振的模态划分成一个子系统,这就有必要对结构内存在的不同波形进行划分。按照模态密度的定义
(15)
式中,cg为上述特征波的群速度。
对于长度为L的波导结构,其振动模态可以看成是该结构为无限长时的一系列成对特征波的干涉结果。每一对特征波幅值相同,相位满足特定关系,沿相反方向传播。那么对于第m种特征波来说,其模态密度可表示为
(16)
式中,cgm为第m种特征波的群速度。
此外,结构中可能存在某些振型相似的特征波,在SEA中,可将这些相似的特征波划分为一个子系统。假设结构中存在M条振型相似的特征波,那么,这种特征波的模态密度可表示为
(17)
可以看出:群速度较低的部分对模态密度贡献比较大,尤其是当群速度为零时,模态密度变得无穷大,这时对应一个新的特征波的出现(cut-on)。换句话说,按照式(17),在截止频率处的模态密度总是为无穷大。因为群速度可以为负值,而模态密度不能为负,因此可把式(17)写成
(18)
将式(11)代入式(18),可得
(19)
3.3 有限频带内的平均模态密度
对于第m种特征波来说,其模态密度由式(16)给出。假定在频带[ω1,ω2]内该特征波存在一个截止频率ω0,那么在频带[ω1,ω2]上的平均模态密度由下式给出
(20)
其中,Δω是一个小的正数。式(20)中的第二个积分的被积函数是连续的,因此积分是有限的。第一个积分的被积函数在ω0处为无穷大,但该积分依然是可积的。因为cgm(ω0)=0,而当ω∈[ω0,ω0+Δω]时,cgm(ω)是光滑连续的,因此cgm(ω)可以近似为cgm(ω)≈μ(ω-ω0)α,μ,α(0<α<1)是正常数。
(21)
由式(21)可以看出,该积分是有限的。这说明即使结构在截止频率处的模态密度为无穷大,但其有限频带内平均模态密度仍然是一个有限值。
3.4 长方形薄板的模态密度
对于面积为S的薄板,其模态密度通常按如下公式计算
(22)
式中:k为同材质同厚度无限大板的特征波数;cg为特征波的群速度。下面从薄板的振动微分方程出发,推导得到式(22)。
考虑宽为b、在x方向无限长的薄板。薄板的两边假定为简支边界条件,频率为ω时的传播波可表示为
(23)
将式(23)代入板的运动微分方程,即可得到板的频散方程
(24)
式中:β为波数;D为板的弯曲刚度;ρ为密度;h为厚度。
通过式(24)可解得对应的波数β为
(25)
进而求得板的群速度为
(26)
对于给定频率ω,板内特征波的数量就是使得式(24)为实数的最大m(记为M(ω))
(27)
根据式(24),对于长度方向为L的有限长薄板来说,此时模态密度可表示为
(28)
将上述求和用积分代替,可得
(29)
可以看出,上面的求和用积分来代替了,相当于将M(ω)个波的模态密度的求和均分到[0,M(ω)]区间内进行积分,进而消除了模态密度在截止频率处的奇异性,使得所求出的模态密度是频率的连续光滑函数。
4 算 例
本节以工程中常见的铝板和高速列车用铝型材为例,计算结构的频散曲线,分析其波动特性。根据频散曲线对不同特征波进行分类,计算结构的群速度和模态密度。
4.1 铝单板
均质铝板的截面如图2所示,宽1 m,厚0.01 m,密度为2 700 kg/m3,泊松比为0.33,弹性模量为7.1×1010Pa。网格采用四节点实体单元,单元长度为0.01 m。板两边的边界条件为自由边界条件。

图2 单板横截面示意图
图3给出了根据式(4)计算得到的单板的频散曲线,曲线上的某点(对应的波数为β、频率为ω)表示结构内存在波数为β、频率为ω的特征波。图 4给出了当波数为4 rad/m时对应的不同频率(43 Hz,59 Hz,435 Hz,1 627 Hz,2 469 Hz,4 167 Hz)下板的二维和三维波形图。从图中可以看出,板内存在很多不同种类的波,如压缩波,剪切波,弯曲波等。
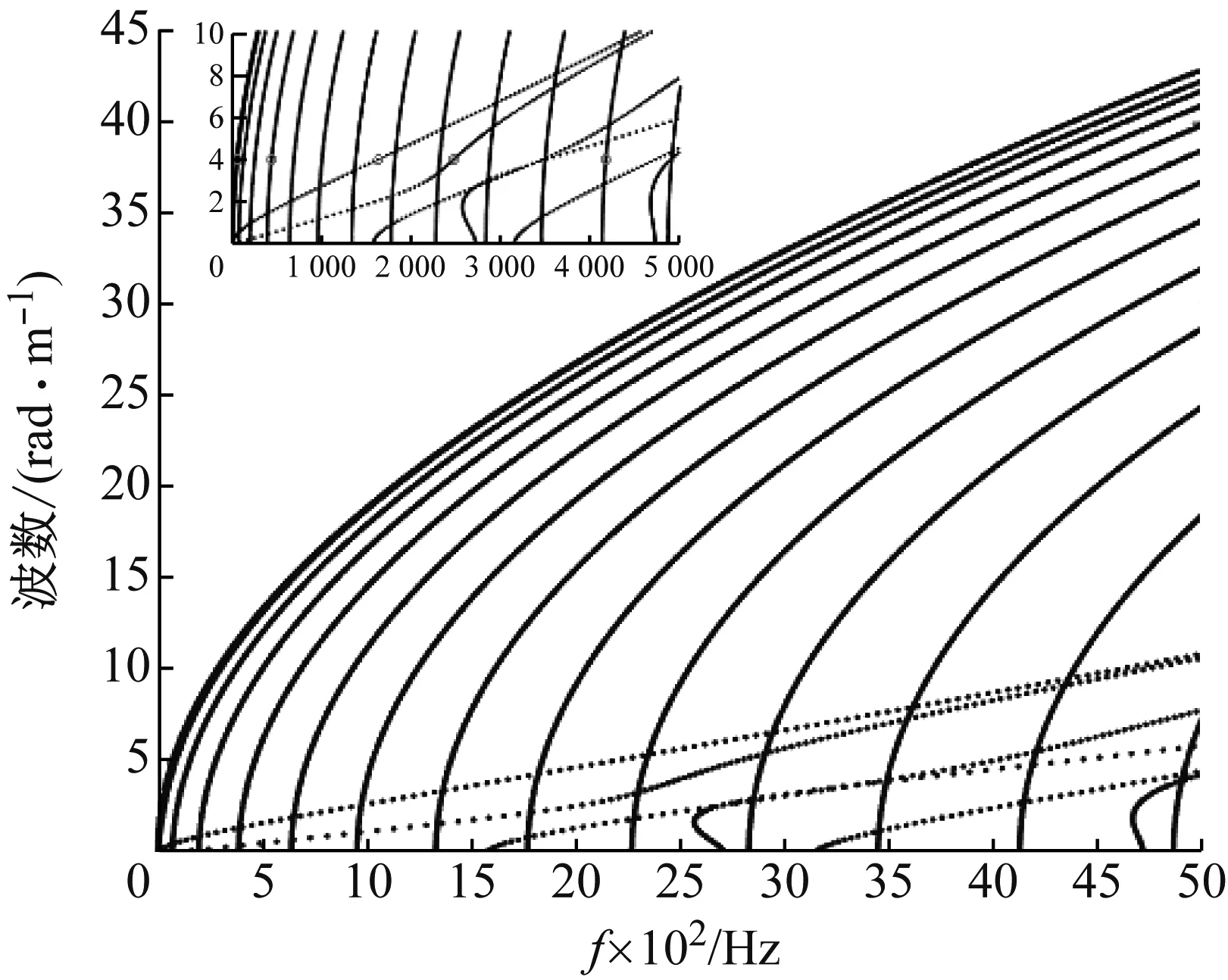
图3 单板的频散曲线
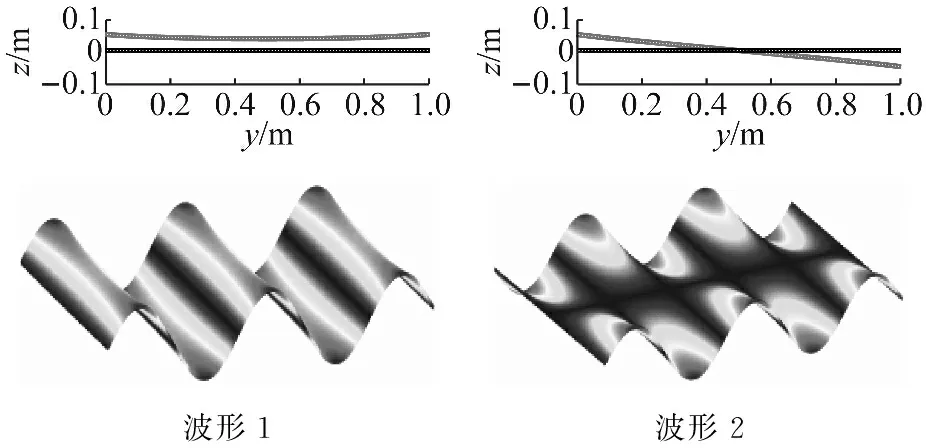
图4 波数为4 rad/m时不同波对应的波形
根据2.1节中提出的WAC值对不同种类的特征波频散曲线进行分类,图5给出了识别后的频散曲线和MAC值,其中图5(a)和(c)中的点划线代表识别后的第1和第5种波的频散曲线,图5(b)和(d)表示对应的WAC值。可以看出,WAC值基本都在0.9以上,说明该方法可以很好的区分结构内存在的不同类型的波。

(a)
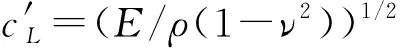
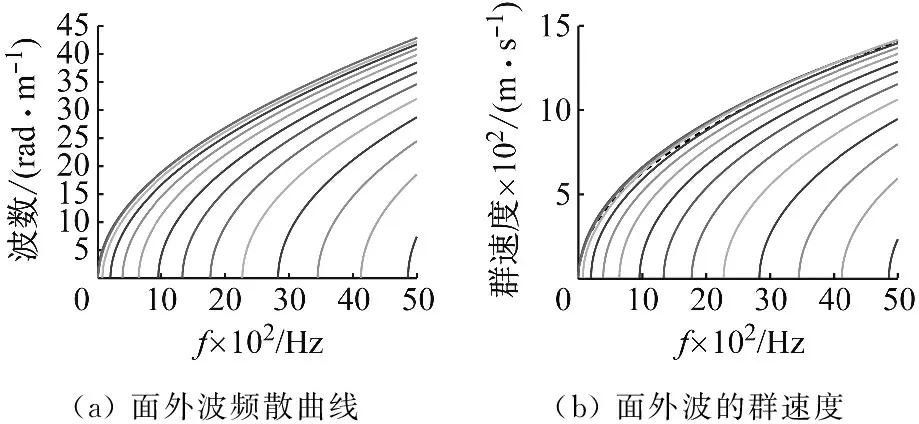
图6 板的面外波和面内波的群速度
图7给出了板在自由边界条件下,长度方向为1 m时,分别根据有限元-模态计数法、2.5维有限元法和板的模态密度的近似公式(即式(22))得到的板的总模态密度。可以看出,对于100 Hz和160 Hz这两个频带,采用有限元-模态计数法得到的频带内的模态密度为零(即板在这两个频带内事实上是没有模态的),而基于2.5维有限元法得到的模态密度和近似公式得到的值相差不大。这是因为,虽然这两个频带的频率比较低,但后两者都对板的振动场均做了混响的假定。随着频率的增大,三种方法得到的模态密度吻合较好。而2.5维有限元法只需对结构的横截面方向进行有限元离散,通过计算三分之一频带上下限处的模态数,即可快速计算结构的模态密度。
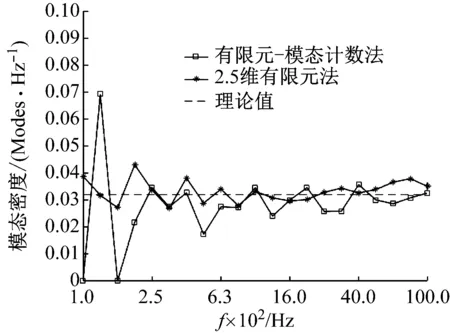
图7 长度为1 m时的板的总模态密度
根据图6给出的不同特征波的群速度,可根据式(11)求出板内不同特征波的模态密度,如图8所示,可以看出,第14和19个波存在负的模态密度。此外,图中的峰值对应于每个波的截止频率。频率一旦跨过此截止频率,一个新的模态波将出现,理论上截止频率处的模态密度为无穷。同时,根据对板的面内波和面外波的分类,可分别得到面内波和面外波的模态密度,如图9所示。可以看出,板的面外波的模态密度要远大于板的面内波的模态密度。
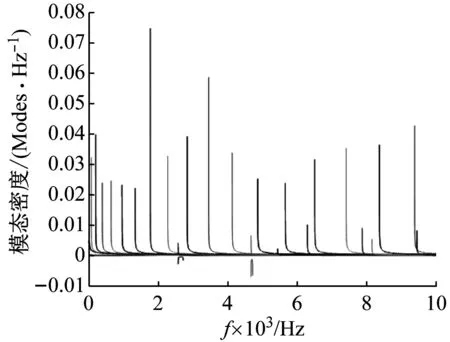
图8 单板不同特征波的模态密度
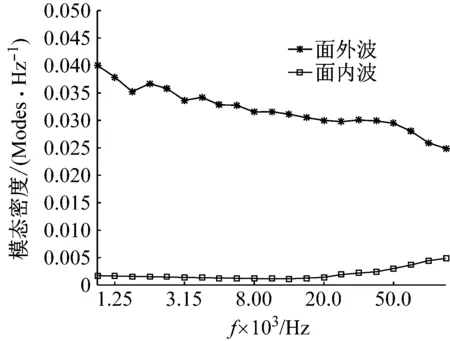
图9 单板面外和面内波的模态密度
前面已经指出,在结构的截止频率处,群速度为零,模态密度为无穷大。在截止频率处,频率间隔的不同可能会导致模态密度不同。图10给出了不同频率间隔(0.5 Hz,1 Hz,10 Hz)的模态密度相对于频率间隔为0.1 Hz的模态密度的相对误差,可以看出,随着频率的增加,相对误差减小,在[100,10 000] Hz内,相对误差基本控制在5%以内。
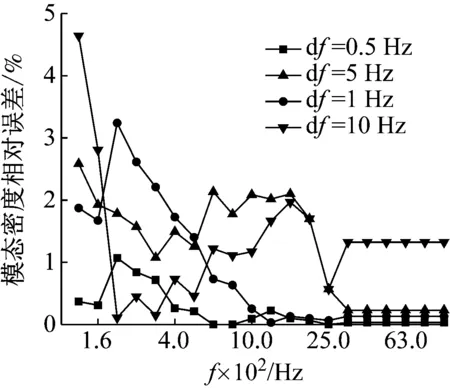
图10 不同频率间隔对模态密度的影响
4.2 铝型材
本节以某高速列车地板铝型材为例,其截面如图11所示,可以看出,该型材由上下面板和22个加筋板组成,截面尺寸为0.970 m×0.050 m,上下两个面板厚度均为4.2 mm,筋板厚度为2.5 mm,实测密度为2 752 kg/m3,弹性模量为7.1×1010Pa,泊松比为0.33。截面网格采用四面体实体单元,单元长度不超过8 mm。两端设置为自由边界条件。

图11 型材截面示意图
图12为根据式(4)计算得到的该型材的频散曲线。可以看出,相对于单板,型材的频散曲线更为复杂。图13给出了波数为4 rad/m时对应的不同频率下的波形图,可以看出,频率较低时,型材表现为整体变形,随着频率的增加,型材开始出现局部变形。
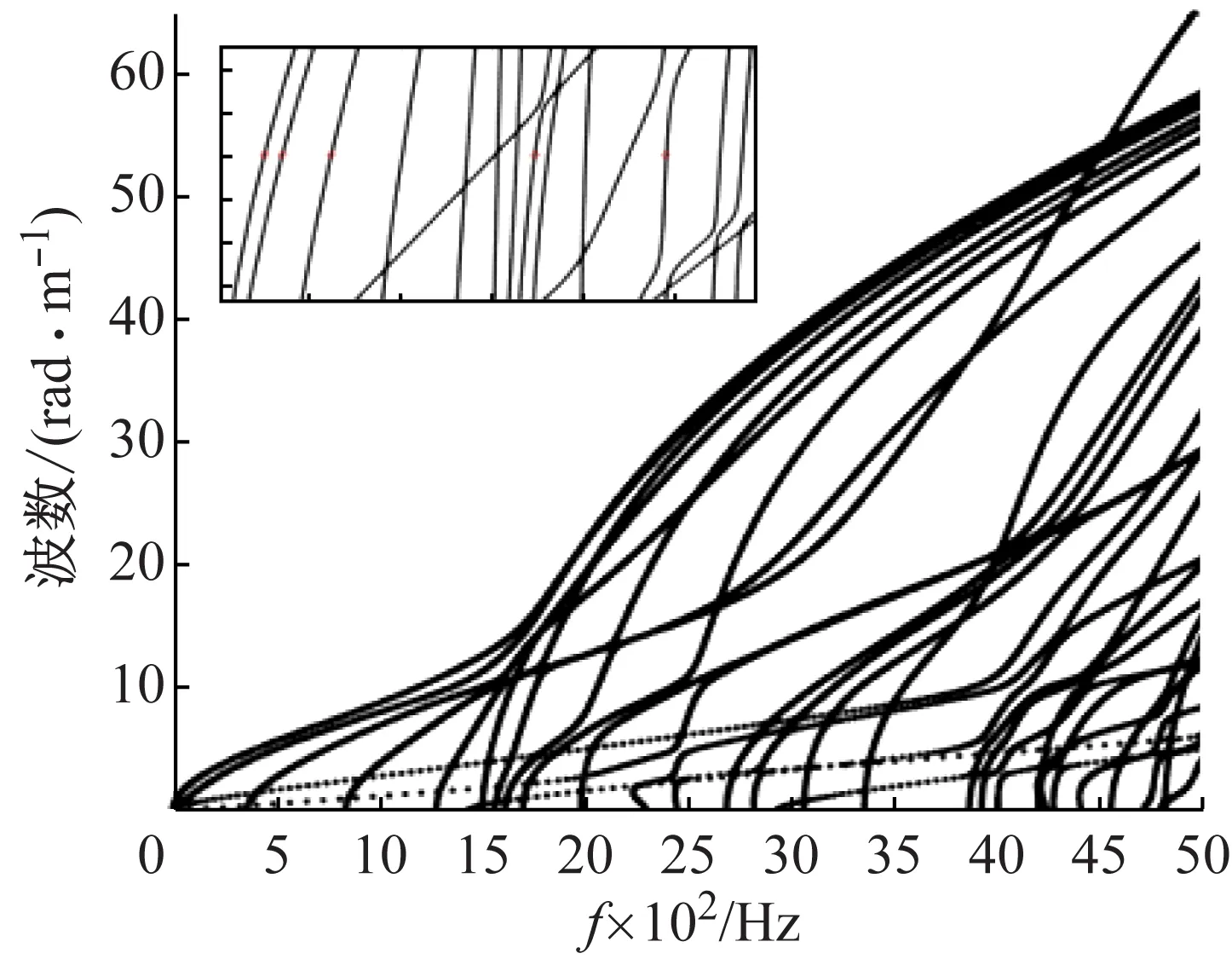
图12 铝型材频散曲线
根据2.1节中给出的WAC准则,可对图11的频散曲线进行特征波的分类,结果如图14(a)所示。与单板不同的是,型材不同的频散曲线之间存在很多交叉点。图14(b)给出了频散曲线的某一部分区域,可以看出,放大后频散曲线有些是交叉在一起的,如图14(b)中的1和2点,这些交叉点的相速度相同,而群速度不同。有些曲线之间并没有交叉在一起,如图14(b)中的3点,这种点一般称之为聚散点(veering point),聚散点处的群速度会发生突变,如图15所示。文献[27]中指出,结构的聚散点对结构的动力学特性有重要影响。在对该点附近的特征波进行分类时,可通过增加波数间隔来实现。

(a)
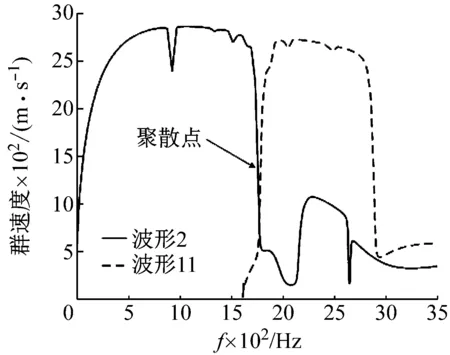
图15 波形2和和波形11对应的群速度
图16给出了分别用本文方法和用有限元-模态计数法得到的长为0.985 m的铝型材的模态密度,其中模态计数法是通过在ANSYS中对型材进行模态分析(单元类型为solid 45,单元尺寸不超过5 mm,边界条件定义为自由边界)得到固有频率,之后通过模态计数法计算三分之一倍频程内的模态数得到,有限元模型在文献[28]中给出。可以看出,基于有限元-模态计数法的模态密度在某些频带内为0,但基于2.5维有限元法计算得到的模态密度则不为0。随着频率的增加,两种方法得到的模态密度吻合越来越好。造成这种差异的原因在于用2.5维有限元法计算结构的模态密度时,利用了梁的群速度和模态密度的近似关系。
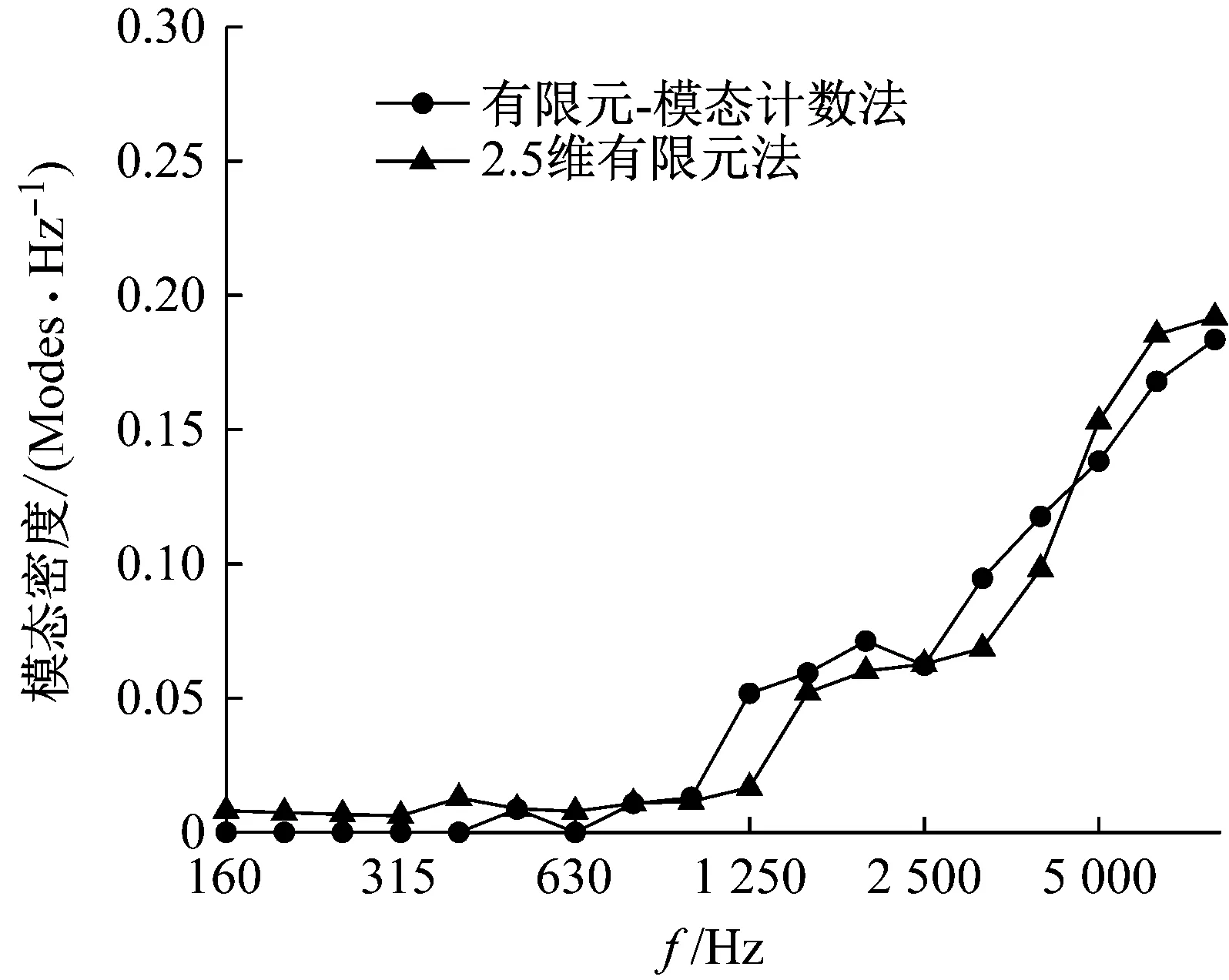
图16 长度为0.985 m的铝型材的模态密度
为了对比两种方法的计算效率,在相同配置的计算机上计算了该型材[0,10 000] Hz内的模态密度,结果表明,有限元-模态计数法用时为8 703 s,而2.5维有限元法用时为1 427 s,由此可以看出本文的方法具有较高的计算效率。
5 结 论
本文基于2.5维有限元法研究了有限长波导结构的波动特性和模态密度,给出波导结构群速度和模态密度的表达式。以单板和型材分析为例,得到以下结论:
(1) 2.5维有限元法从结构的波动特性出发,通过对结构的特征波进行分类,能够实现不同特征波的模态密度的计算。
(2) 频散曲线上波数为零的点为结构的截止频率,一旦超过该频率,一个新的波将出现。截止频率处群速度为零,模态密度为无穷大,但在任何一个有限的频率区间内的积分是有限的。
(3) 在某些截止频率附近,结构的某些特征波可能存在负的群速度和模态密度,这意味着波的传播方向和波所携带的能量的传播方向相反。
(4) 基于2.5维有限元法推导单板模态密度的公式,将有限个波的模态密度叠加变换到有限区间内进行积分,可消除模态密度在截止频率处的奇异性,使得所求出的模态密度是频率的连续光滑函数。
(5) 随着频率的增加,本文方法计算得到的模态密度和其他方法吻合较好,验证了本文方法的有效性。
