频域稀疏采样和激光成像方法*

崔岸婧 李道京 吴疆 周凯 高敬涵

1) (中国科学院空天信息创新研究院,微波成像技术国家级重点实验室,北京 100190)

2) (中国科学院大学,北京 100049)

激光的单色性和自然图像频谱稀疏且集中在低频区间的特点,使图像频谱稀疏采样成像成为可能.基于小规模激光探测器,引入参考激光,本文提出了频域稀疏采样激光成像方法.介绍了频域稀疏采样激光成像的原理和成像系统结构,推导了激光回波重构复频谱的表达式,给出了重构频谱和复图像的仿真结果并分析了信号参数对重构效果的影响,同时采用相干系数、均方误差和结构相似度来评价其重构效果.规模为256 × 256的激光回波复图像仿真表明,5 个拼接1/4 × 1/4 规模频域探测器组成的近似十字型稀疏采样结构,在约31.25% (5/16)的频域稀疏采样条件下,仍可获得较好的重构频谱和重构复图像.

1 引言

目前大规模可见光探测器相机已达到30k ×30k 量级,高分辨率宽幅成像的需求在推动探测器规模不断扩大的同时,也产生了数据量大、传输和处理困难等问题.

前端先大数据量采集,然后后端再数据压缩,这似乎是一个前后矛盾的过程.激光具有窄带性和单色性,由傅里叶光学成像4f实验[1,2]和文献[3,4]可知,利用激光探测获取的目标信号在频域稀疏且频谱集中在低频区间.在此基础上,利用傅里叶透镜将激光图像变换到频域,在其低频区间实施稀疏采样,进一步通过反演实现激光成像具有可行性.

将小规模面阵探测器设置在激光回波频谱低频区间,用频域稀疏采样的方式可等效对激光回波复图像的二维低频滤波,在仅丢失图像部分高频信息的情况下,以小幅牺牲分辨率为代价减少图像数据量,或可大幅缓解探测器规模和高分宽幅成像的矛盾.近年快速发展的计算成像技术[5]为频域稀疏采样激光成像思路提供了一定程度的理论和实践支持,如文献[6,7]将傅里叶叠层成像技术用于远距离遥感成像问题.

文献[8]探讨了图像频域稀疏激光成像问题,给出了一些初步仿真结果,基于激光本振相干探测技术体制,其技术实现原理清楚.2020 年美国Point Cloud 公司基于硅光芯片的FMCW 激光雷达相干阵列探测器(阵元规模为512(32 × 16))[9],使频域稀疏采样激光成像成为可能.考虑到目前大量应用的激光探测器仍然采用没有激光本振的直接探测体制,主要实现信号平方律检波功能,为便于区分,本文将其简称为直接探测器,本文在文献[8]和时域相干探测[10]的基础上研究了基于直接探测器的频域稀疏采样激光成像问题.

2 频域稀疏采样激光成像原理

基于直接探测器的频域稀疏采样成像系统结构如图1 所示,其中F 为经接收望远镜聚焦后的激光回波复图像,下文将激光回波复图像简称为激光回波,f表示傅里叶透镜的焦距.激光器发射相同的两束激光,其中一束用于照射目标以获取激光回波,另一束作为参考激光,经空间相位调制后用于激光回波频谱的重构.激光回波经过傅里叶透镜处理,其频谱和参考激光的相干光由直接探测器接收.空间光调制器采用时分方式,对参考激光实现0°和90°相移处理,以获取激光回波频谱的实部和虚部.为减少数据量,采用小规模面阵直接探测器,并在低频区由5 个1/4×1/4 规模频域探测器构成十字型.

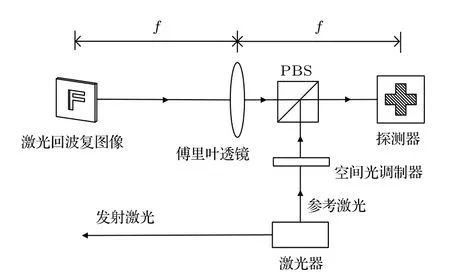
图1 基于直接探测器的频域稀疏采样成像系统结构Fig.1.Structure of the frequency-domain sparse sampling imaging system based on direct detector.

在对基于频域直接探测器的复图像重构过程进行分析前,做出以下假设:

1)面阵探测器中各直接探测像元位于x-y平面上;

2)频域采样过程中,激光器、目标和傅里叶透镜之间的距离固定,激光由激光器传播至傅里叶透镜所经过的光程为定值;

3)在空间光调制器对参考激光做0°和90°相移过程中,激光回波复图像保持不变;

4)参考激光的幅度远大于激光回波频谱的幅度.

激光回波为复信号,经过傅里叶透镜处理后所得频谱为复数,因此可设置激光回波频谱的表达式为

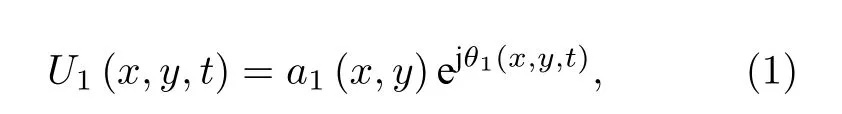
双路参考激光的表达式为

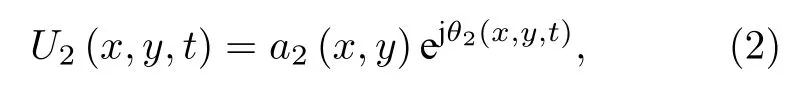
参考激光经空间光调制器相移90°后的表达式为

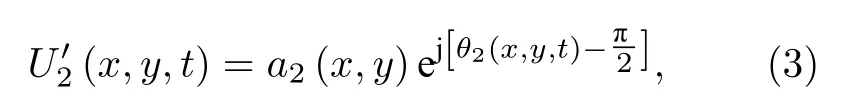
式中,a1(x,y)和a2(x,y) 分别为回波频谱和参考激光在探测器平面上的幅度,θ1(x,y,t)=2πf0t+φ1(x,y)和θ2(x,y,t)=2πf0t+φ2(x,y) 分别表示回波频谱和参考激光在探测器平面上的相位,f0为激 光 载 频,t为 快 时 间,φ1(x,y)和φ2(x,y) 分 别 为回波频谱和参考激光在探测器平面上坐标 (x,y) 位置上的初始相位.

文献[10]表明,同源同频(同波长)参考激光和激光回波具有时域相干性,傅里叶透镜对每个快时间时刻的激光回波复图像在二维空间域做傅里叶变换,并未改变激光回波的时域相干性,因此激光回波频谱与参考激光在时域也具有相干性.

激光回波频谱和参考激光在探测器平面上相干后的光强[11,12]为

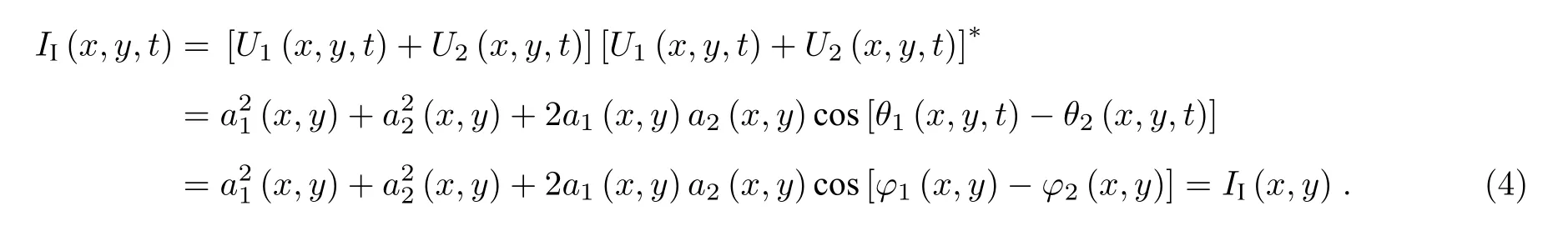
激光回波频谱和相移90°后的参考激光在探测器平面上相干后的光强为

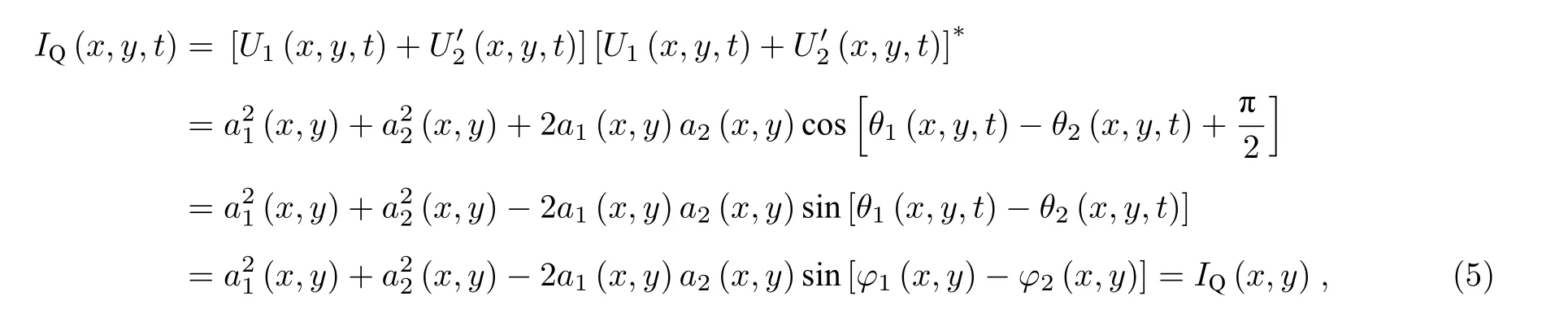
式中,*表示信号的共轭,θ1(x,y,t)-θ2(x,y,t)=φ1(x,y)-φ2(x,y)消除了激光载波的影响.

由假设3)可得a2(x,y)≫a1(x,y),因此(4)式和(5)式中的(x,y) 可忽略.用功率计可获取参考激光的光强(x,y),经换算可将(4)式和(5)式转化为激光回波频谱实部和虚部的表达式

由(6)式和(7)式组合可得复频谱

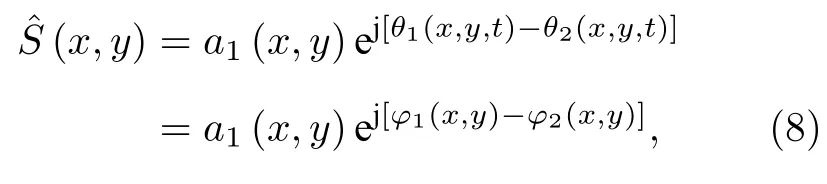
因θ1(x,y,t)-θ2(x,y,t) 仅为x-y平面上的变量,该复频谱在任意时刻固定.(8)式所示复频谱与激光回波频谱a1(x,y)ejφ1(x,y) 存在相位差,当参考激光的初始相位φ2(x,y)=0 时,激光回波频谱恢复效果较好;当参考激光的初始相位φ2(x,y)=π/2时,激光回波频谱的幅度仍能较好恢复,但重构频谱与激光回波频谱正交.

当设置参考激光的初始相位为0 时,(8)式重构频谱经傅里叶逆变换可得激光回波,即实现图像的重构.

3 频谱与图像重构的仿真分析

目前涉及激光雷达回波复图像研究的文献不多,与微波成像雷达[13]类似,激光成像雷达回波信号[14]的初始相位也应由目标斜距决定,因此激光回波复图像的相位与其幅度应具有强相关性,部分傅里叶叠层成像文献[15,16]对复图像的幅度和相位不建立相关性,会造成复图像物理意义不明确.

受实验条件所限并使问题简化,本文仿真中假定激光回波复图像的相位与其灰度图相同,傅里叶叠层成像[4,6,7]研究工作中也常做这种假定.

图2 给出本文仿真分析所用的像素规模为256 × 256 的复图像幅度图,设置该复图像的相位图与幅度图一致,且相位的变化范围设置为0— 2π.根据第2 节中推导仿真激光回波频谱和图像的重构.本文在仿真中设置参考激光和激光回波频谱的幅度关系为a2(x,y)=30μ[a1(x,y)],a2(x,y) 为不随x和y变化的固定值,参考激光的初始相位φ2(x,y)=0,其中μ(·) 表示取均值,实际工作中可在没有参考激光的条件下用频域直接探测器大致估计a1(x,y) 的均值.

图2 激光回波复图像幅度图Fig.2.Laser echo complex image amplitude diagram.

3.1 面阵探测器重构频谱和图像

在面阵中满布256 × 256 个直接探测器的情况下,仿真激光回波频谱和图像的重构,仿真结果如图3 至图5 所示.由仿真结果可见,面阵探测器重构图像与激光回波图像基本一致.

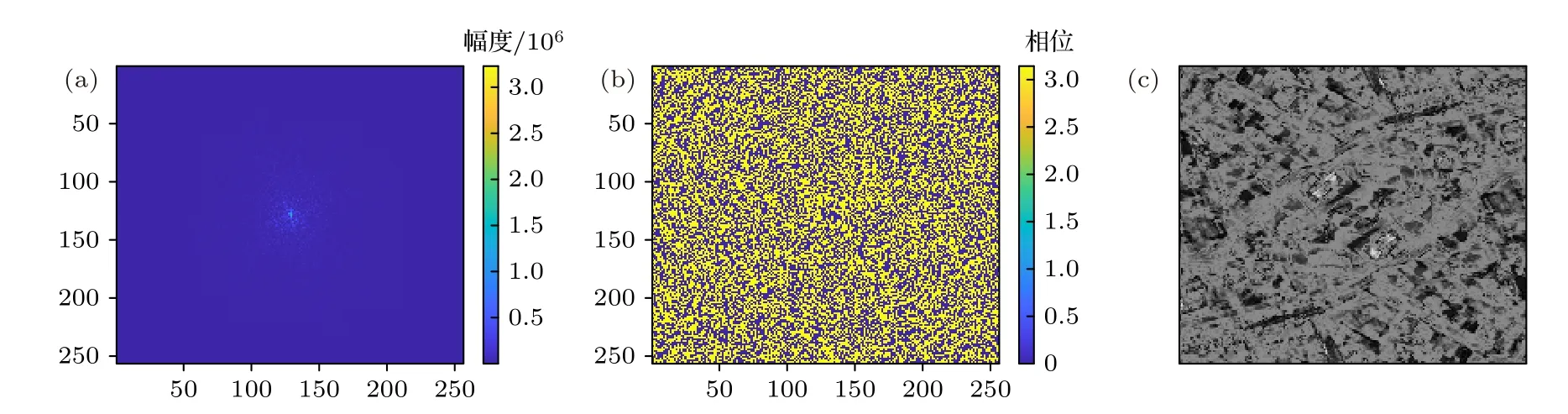
图3 面阵探测器频谱实部重构 (a)频谱幅度;(b)频谱相位;(c)图像Fig.3.Reconstruction of the real part of the plane array detector signals’ spectrum:(a) Amplitude of the spectrum;(b) phase of the spectrum;(c) image.

3.2 稀疏面阵探测器重构频谱和图像

用5 个1/4×1/4 规模频域直接探测器拼接构成十字型的情况下,仿真激光回波频谱和图像的重构,探测器范围如图6 所示,仿真结果如图7 至图9所示.图9 与图5 对比可见,面阵探测器重构复图像效果优于十字型探测器重构复图像,频域稀疏导致激光回波频谱部分信息损失.

图4 面阵探测器频谱虚部重构 (a)频谱幅度;(b)频谱相位;(c)图像Fig.4.Reconstruction of the imaginary part of the plane array detector signals’ spectrum:(a) Amplitude of the spectrum;(b) phase of the spectrum;(c) image.

图5 面阵探测器频谱重构 (a)频谱幅度;(b)频谱相位;(c)图像Fig.5.Reconstruction of the plane array detector signals’ spectrum:(a) Amplitude of the spectrum;(b) phase of the spectrum;(c) image.

图6 5个1/4 × 1/4 规模频域探测器拼接构成十字型探测范围Fig.6.Cross detection range constituted by five 1/4 × 1/4 scale frequency domain detectors.

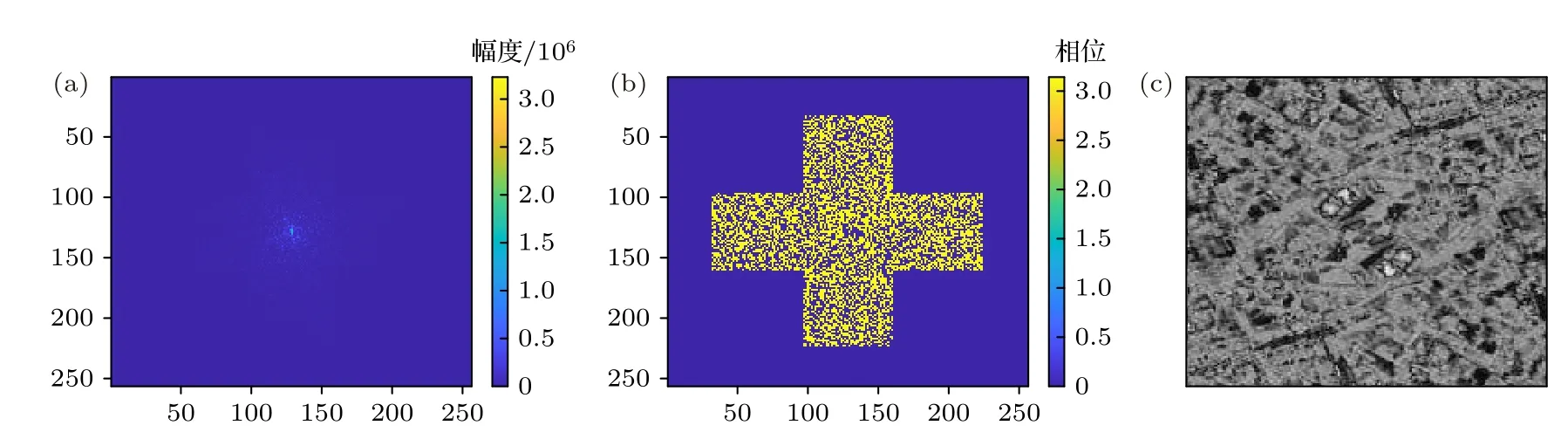
图7 稀疏面阵探测器频谱实部重构 (a)频谱幅度;(b)频谱相位;(c) 图像Fig.7.Reconstruction of the real part of the sparse plane array detector signals’ spectrum:(a) Amplitude of the spectrum;(b) phase of the spectrum;(c) image.

图8 稀疏面阵探测器频谱虚部重构 (a)频谱幅度;(b)频谱相位;(c)图像Fig.8.Reconstruction of the imaginary part of the sparse plane array detector signals’ spectrum:(a) Amplitude of the spectrum;(b) phase of the spectrum;(c) image.

图9 稀疏面阵探测器频谱重构 (a)频谱幅度;(b)频谱相位;(c)图像Fig.9.Reconstruction of the sparse plane array detector signals’ spectrum:(a) Amplitude of the spectrum;(b) phase of the spectrum;(c) image.

3.3 重构效果评价

本文采用相干系数[17]、均方误差和结构相似度[18,19]评价激光回波复图像和频谱的重构效果.以下将在面阵探测器和稀疏面阵探测器的条件下,根据(8)式重构所得频谱及其经傅里叶逆变换所得复图像分别定义为面阵探测器重构频谱、面阵探测器重构复图像、稀疏面阵探测器重构频谱和稀疏面阵探测器重构复图像.

相干系数表示重构复图像(频谱)与激光回波复图像(频谱)之间的线性关系,其范围为 [0,1],当相干系数接近1 时,复图像(频谱)的重构效果越好,其定义式为

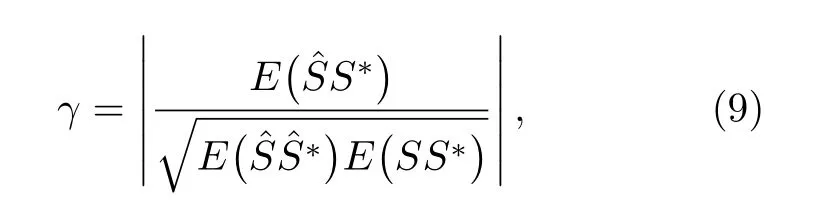
式中,E(·) 表示计算数学期望,也可用平均值替代,S为激光回波复图像或频谱,为重构复图像或频谱.

均方误差表征重构复图像(频谱)与激光回波复图像(频谱)的差异程度,其表达式为

式中N表示复图像(频谱)的规模,本文中N=256×256 ;和si分别表示重构复图像(频谱)和激光回波复图像(频谱)中第i个单元的值.均方误差越小,表示重构效果越好.

结构相似度从对比度、亮度和结构等角度评价复图像(频谱)的重构效果,其表达式为

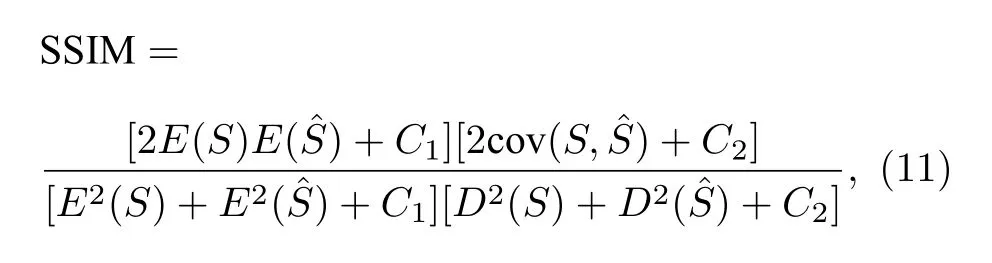
式中,D(·)表示计算方差,cov(·) 表示计算协方差,C1和C2均为常数矩阵.结构相似度的范围为 [0,1],当 SSIM=1 时,两幅复图像(频谱)完全相同;当SSIM=0时,两幅复图像(频谱)不相关.

面阵探测器和稀疏面阵探测器重构频谱和复图像的相干系数、均方误差和结构相似度如表1所示.由相干系数和均方误差可见稀疏面阵探测器的频谱重构效果较好,但由于利用傅里叶逆变换重构复图像对频谱的精确度较高,因此稀疏面阵探测器重构复图像结构相似度明显降低,均方误差增大.

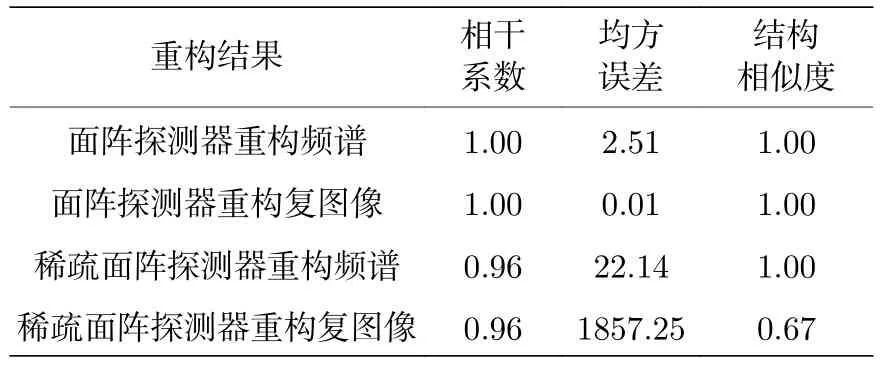
表1 面阵探测器和稀疏面阵探测器频谱与复图像重构效果Table 1.Spectrum and complex image reconstruction effect of the plane array detectors and the sparse plane array detectors.

3.4 参数变化的影响分析

上述仿真和分析均基于参考激光和激光回波频谱幅度满足a2(x,y)=30μ[a1(x,y)],参考激光的初始相位φ2(x,y)=0 的条件,以下基于相干系数分析幅度比值和φ2(x,y) 对重构效果的影响.

图10 为φ2(x,y)=0条件下,不同R对应的稀疏面阵探测器重构复图像的相干系数曲线.

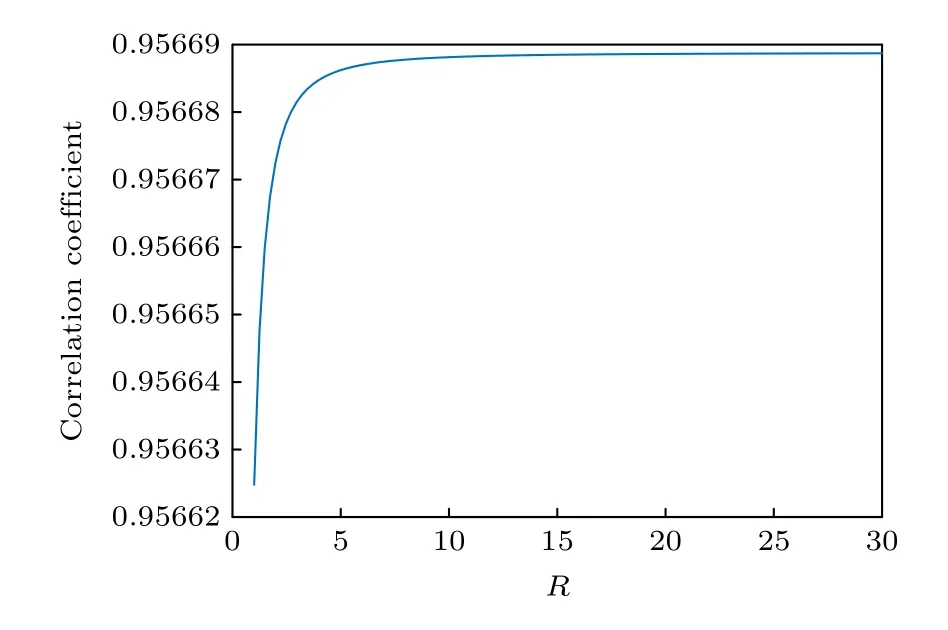
图10 R 与稀疏面阵探测器重构复图像相干系数的变化曲线Fig.10.Change curves of the relationship between R and correlation coefficient of the reconstructed complex image of the sparse plane array detectors.

由仿真结果可知,参考激光幅度和激光回波频谱幅度均值的比值R的增大可提升复图像的重构性能.当R →30时,相干系数的增大趋于平稳.R=30条件虽在一定程度上牺牲了探测器的动态范围,但能够保证获得较好的重构结果.

图11 为R=30条件 下,不 同φ2(x,y) 对应稀疏面阵探测器重构复图像的相干系数曲线.结果表明,参考激光的初始相位对激光回波复图像的重构效果没有明显的影响.

图11 φ2(x,y) 与稀疏面阵探测器重构复图像相干系数的变化曲线Fig.11.Change curves of the relationship betweenφ2(x,y)and correlation coefficient of the reconstructed complex image of the sparse plane array detectors.

4 结论

本文研究了基于直接探测器的稀疏频域采样成像方法并给出了仿真结果,分析结果表明该方法具有一定可行性,后续将开展验证实验.

为基于直接探测器重构复频谱,本文方法采用时分方式对参考激光实现的空间相位调制,这对高数据率成像造成了一定影响,因此本文方法适用于场景变化缓慢、需求对时效性要求不高的情景.与此同时,该方法要求参考激光的幅度较大,这在一定程序上降低了探测器的动态范围.

本文在复频谱重构过程中引入参考激光,其思路和数字全息成像[20,21]有相近之处.目前的数字全息成像采样在图像域完成,其重构工作主要是为了恢复图像的幅度(灰度),对其相位的重构效果较差,将本文方法用于数字全息成像,不以稀疏采样减少数据量为目的时,有可能获得比现有数字全息方法更好的复图像重构效果,持续相关研究工作具有重要意义.