基于图像重构的MNIST对抗样本防御算法

秦中元，贺兆祥，李涛,2，陈立全,2

基于图像重构的MNIST对抗样本防御算法

秦中元1，贺兆祥1，李涛1,2，陈立全1,2

（1. 东南大学网络空间安全学院，江苏 南京 211189；2. 网络通信与安全紫金山实验室，江苏 南京 211189）

随着深度学习的应用普及，其安全问题越来越受重视，对抗样本是在原有图像中添加较小的扰动，即可造成深度学习模型对图像进行错误分类，这严重影响深度学习技术的发展。针对该问题，分析现有对抗样本的攻击形式和危害，由于现有防御算法存在缺点，提出一种基于图像重构的对抗样本防御方法，以达到有效防御对抗样本的目的。该防御方法以MNIST为测试数据集，核心思路是图像重构，包括中心方差最小化和图像缝合优化，中心方差最小化只针对图像中心区域进行处理；图像缝合优化将重叠区域纳入补丁块选取的考量，并以补丁块的1/2大小作为重叠区域。使用FGSM、BIM、DeepFool以及C&W攻击方式生成对抗样本来测试两种方式的防御性能，并与现有的3种图像重构防御方式（裁剪与缩放、位深度压缩和JPEG压缩）效果对比。实验结果表明，所提中心方差最小化和图像缝合优化算法，对现有常见对抗样本的攻击起到了较好的防御效果。图像缝合优化对4种攻击算法生成的样本分类正确率都达到了75%以上，中心方差最小化的防御效果在70%左右。而用作对比的3种图像重构算法则对不同攻击算法的防御效果不稳定，整体分类正确率不足60%。所提中心方差最小化和图像缝合优化两种图像重构防御算法达到了有效防御对抗样本的目的，通过实验说明了所提防御算法在不同对抗样本攻击算法中的防御效果，另外，将其他图像重构算法与所提算法进行比较，说明了所提算法具有良好的防御性能。

对抗样本；图像重构；深度学习；图像分类

0 引言

自从深度学习的理论被提出以来，人们从未停止研究的脚步，并且在计算机视觉、语音数据处理以及自然语言处理等领域取得了显著进展。对抗样本是在不同的图像中添加微小的扰动[1]，这样的扰动在人眼看来并没有太大的差别，却能够改变神经网络对原有图像的分类结果，这无疑是人工智能发展的严重阻碍。

对抗样本在实际应用场景中的攻击行为越来越受到研究者的重视。自动驾驶中的核心技术就是环境识别系统，在行驶过程中需要识别周围环境中的路况和各种标志。研究发现，原本是表示停止标识的3块交通指示牌，在添加扰动后均被识别为限速标志，这无疑会让驾驶系统发出错误的行驶指令，甚至造成严重的交通事故[2]。由此可见，深度学习中的识别系统并不是完全安全可信的，如果以后自动驾驶逐渐普及，而有人恶意使用对抗样本手段来进行攻击，那将会严重威胁自动驾驶技术的发展和大众的人身安全。

图像分类是人工智能技术的重要领域之一，而且攻击者已经实现对于卷积神经网络的有效攻击。文献[3]通过对“小狗”“电器”等图像添加扰动，卷积神经网络将其识别为“鸵鸟”类型，造成了精准的攻击，这将对图像分类任务造成重大威胁。对抗样本的问题在人脸识别中同样存在。现有人脸识别系统中，已经加入对常见对抗样本攻击的防御措施，然而仍然有新的对抗样本攻击方法提出。在人脸图片中不加入扰动，以高亮的贴片来混淆人脸系统的识别结果。一种攻击方式方法是，在原始图像中未添加扰动，只是戴上一个贴片形式的眼镜，就能够欺骗识别系统。如果该方法应用到刷脸支付场景中，将造成严重的财产安全问题[4]。

为消除图像中的对抗性扰动，传统图像变换方式是通过对图像数据集进行处理，如通过图像旋转的方式使对抗样本的攻击失效。显然类似的图像处理方法相比对抗样本的产生过程过于简单，只能以试探性的方式来抵御对抗样本的攻击。同时，对图像的旋转等操作，降低了神经网络对干净样本的分类正确率。因此，以图像处理的方式提高分类模型对于对抗样本的鲁棒性，需要更加复杂的图像处理。

因此，设计一种不依赖于图像特征和神经网络分类模型的对抗样本防御方法具有重要意义。卷积神经网络对图像进行特征提取、设定模型参数、训练网络模型等操作，获得了对图像的识别和分类处理功能。然而对抗样本的攻击在神经网络中真实存在，为了保证神经网络的安全性和可靠性，需要考虑如何防御对抗攻击。现有的对抗性训练方式主要根据原始图像和对抗样本的特征差异，训练具有鲁棒性的深度学习模型[5]，但该方式存在过拟合以及可迁移性不强等问题[6]。本文提出了一种新的图像重构对抗样本防御方法，该方法完全独立于分类模型，具有明显的可迁移性和普适性，能够显著提高目标分类器对于对抗样本的分类正确率，从消除扰动入手，原理上具有很好的可解释性。

1 相关工作

1.1 现有对抗样本攻击方法

从对抗样本的生成机理方面，可将攻击方法分为基于梯度优化的攻击算法和基于约束优化的攻击算法。基于梯度优化的生成对抗样本典型算法有快速梯度符号法（FGSM）[7]、基本迭代法（BIM）[8]和DeepFool[9]；基于约束优化的对抗样本生成算法包括C&W[10]算法等。

（1）快速梯度符号法

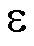
（2）基本迭代法

基本迭代法是FGSM诸多变式中的一种，BIM的改进方案是在干净样本上有限次数地迭代使用FGSM添加对抗性扰动，从而在约束条件内生成更强大的对抗样本，如式(2)所示。

（3）DeepFool

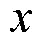
（4）C&W算法

C&W算法的核心是将约束优化策略转换为无约束优化的经验损失函数。

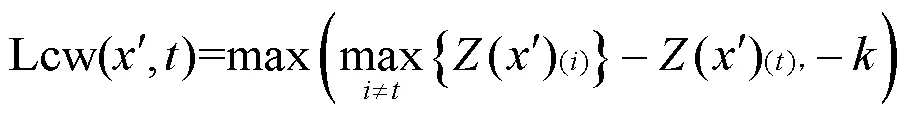
1.2 现有基于图像重构的对抗样本防御方法

图像重构是对图像进行裁剪、压缩等方式，生成新的图像，新图像生成的目标是尽可能多地去除输入样本的干扰信息，同时分类模型能够对数据集进行正确分类。满足以上条件的图像处理方式，主要有图像裁剪和缩放、位深度压缩以及JPEG压缩等方式。

Dziugaite等[14]提出了在对抗样本中使用JPEG的方法消除对抗性扰动。在其实验结果中，针对FGSM需要在较小扰动下才有一定的防御效果，但其对抗性仍然存在，处理后的分类正确率整体小于干净样本。另一种是以图像重新缩放来进行对抗样本去除扰动[15]，Lu[16]使用FGSM和BIM来生成对抗样本，并使用YOLO目标检测算法来测试在现实世界中的识别成功率。实验结果表明，针对这两种算法的攻击，目标检测算法仍然能保持一定的识别成功率，但文献[16]并未针对现有攻击性更强的算法来进行测试，无法说明通过图像缩放的方式能有效抵御所有对抗样本的攻击。

Guo等[17]提出了通过总方差最小化和图像缝合[18]算法进行防御的思路，重构后的图像有较高的分类正确率，说明了该方法的合理性。总方差最小化算法计算整幅图像的总方差计算量巨大，耗费时间长，图像缝合算法中对图像的尺寸要求较大，补丁块较小时不能反映图像的特征[19]，存在一定的优化空间。

2 本文算法

2.1 算法框架

使用图像重构防御对抗样本存在以下两个问题：如何保证修改的信息能够去除对抗性扰动；如何在修改原始输入后减少分类模型对干净样本的分类影响。

针对以上两个在修改输入过程中所面临的问题，本文将两种图像处理中的算法进行优化并结合使用，适应于对抗样本的防御工作。本文算法包括中心方差最小化（TVM，total variance minimization）和图像缝合（image quilting）优化两个步骤，具体原理框架如图1所示。

图1 图像重构原理框架

Figure 1 Image reconstruction principle framework

中心方差最小化是以一个最小的差别将原始图像中心区域重构，重构后的图像能够去除对抗样本算法所添加的扰动信息。图像缝合是通过建立一个图像补丁库的方式，对输入的图像进行打补丁，建立补丁库只使用干净样本，破坏了对抗样本在图像中的结构，提高了图像的分类准确率。

2.2 基于中心方差最小化的图像重构防御

（1）总方差最小化

总方差最小化算法是以图像压缩方式将图片重构的方法，在压缩过程中因限制了变化的总方差最小而得名，该算法的基本原理如下。

然后，对于该集合可重构出一张图片，此时所复现的图像是一个最简单的图像，可能与原始图像相差很大，那么采用计算方差的方式代表重构后与原始图像的差别，即目标函数为

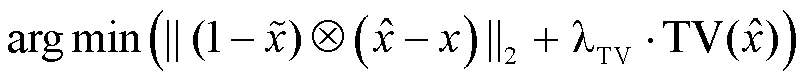
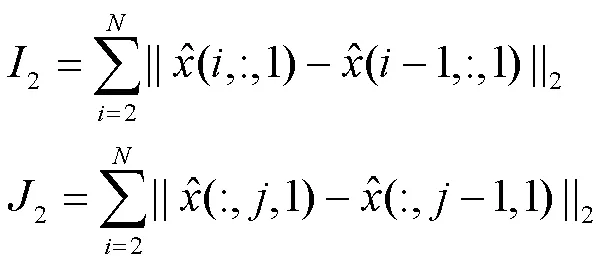
（2）算法改进

针对总方差最小化算法在重构过程中计算量大、耗费时间长等缺点，本文对其改进为中心方差最小化算法，仅对图像的中心区域计算方差，具体优化如下。

在优化方面，本文对图像的中心区域进行重构。在本文处理的MNIST手写数字图像数据集中，每幅图像的尺寸为28×28。该灰度图像中数字的大小占整体尺寸的40%～90%。因此，对中心区域进行处理，实际处理过程选取14×14大小的图像进行重构，其余位置不作处理。原理演示过程如图2所示。

图2 中心尺寸选取演示

Figure 2 Illustration of center size selection

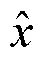
单幅图像中的多个特征向量与原始图像的像素点进行逐元素相乘，该过程以方差和最小为目标函数进行计算，最后，将修改后的像素点重构为新的图像，该图像将代表重构前的图像进入分类模型进行分类。在该过程中，主旨思想是在提取特征向量后进行多次计算，以重构像素点和选取像素点的方差和最小为目标，所重构出的图像中能有效去除对抗性扰动。

2.3 基于图像缝合优化的图像重构防御

（1）图像缝合算法

图像缝合最初用于生成纹理图像[18]，当两幅图像的纹理统计信息相匹配，在人们的心理预期中这两幅图像是相似或者基本相同的。在防御对抗样本中，图像缝合使用补丁对图像进行重构，在加入补丁时采用补丁覆盖原始区域的方式进行，并采用近邻原则选取合适的补丁来对图像进行重构。同时，要求补丁块图像和原始图像尽可能相似，二者之间的欧几里得距离代表相似度，因此，计算补丁块和原始图像块的距离，选取=1，将所有补丁块分为两类。满足距离条件较小的补丁块和原始图像块的相似度也较高，在符合距离条件较小的补丁块中随机选取一个来覆盖原始图像中的相应位置。评定补丁块和原始图像块的相似度标准如下。

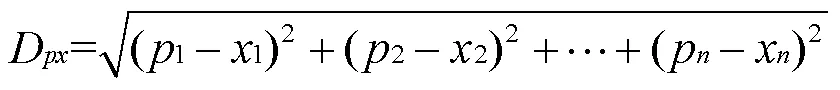
其中，是待重构图像和补丁块的欧几里得距离，为一个补丁块的像素点总个数。当补丁块和原始图像的相似度较高时，使用补丁块图像来代替原始图像块，当整幅图像全部由补丁块进行替换时，图像重构完成，图像缝合的流程描述如图3所示。

Figure 3 Flowchart of image quilting algorithm

图像缝合算法的实现过程中应用了干净样本来创建补丁块数据库，将该数据库应用于缝合过程中补丁块的选取，去除了缝合前图像中的扰动信息，经过缝合重构的图像完全是由干净样本的图像块组成的，因此能在神经网络中有良好的分类表现。另外，在图像缝合过程中，选取了近邻的补丁块中空间距离较小的补丁块，这样重构的图像能满足在误差范围内的要求，尽可能达到整体误差最小的目标。但是，该算法设计时采用ImageNet中尺寸为224×224的图像数据集，需要的图像尺寸较大，针对其他数据集不能很好地适应，重构后的图像在拼接边缘存在分界明显等缺点，仍存在一定的优化空间。

（2）图像缝合算法的优化

针对MNIST图像尺寸较小的特征情况，对图像缝合算法进行适度改进和优化。在原始图像缝合中，需要待缝合的图像尺寸较大，能够分割出足够多的补丁块位置，并从数据库中选取补丁块来进行缝合。MNIST图像不能像ImageNet图像一样提供224×224大小的尺寸，并且可以划分为多块。对此，结合MNIST图像的尺寸特征，本文选取4×4大小的正方形作为分割块，将图像按行和列分割为13×13个补丁块位置。

在创建补丁块数据库的过程中，选取10 000张MNIST干净样本，将其划分为补丁块添加到数据库中，在进行图像缝合时将数据库中的补丁块与图像中的位置进行匹配，按照从左到右、从上到下的顺序依次进行，图片缝合的模拟演示过程如图4所示。当一幅图像上的所有位置匹配完成时，该图像重构完成，代替缝合前的图像进入分类模型中。

图4 图像缝合过程重叠区域演示

Figure 4 Illustration of overlapping areas during image quilting process

为了解决补丁块拼接边界不平滑的问题，设定相邻补丁块之间存在一定的重叠区域，该区域设定为4×2大小，即每个补丁与右侧或下方的重叠区域占总面积的1/2。

3 实验与分析

3.1 中心方差最小化

（1）运行时间

计算方差纯粹依赖CPU的性能而无法使用GPU进行加速，所以运行速度相当缓慢，本文采用的中心方差最小化是对原算法计算效率的优化。在本实验中所使用的硬件设备为Intel i7处理器和8 GB运行内存，软件环境为库函数numpy，实验结果如表1所示。

表1 总方差和中心方差最小化算法性能对比

由表1中数据可以看出，在使用MNIST原始尺寸时，重构100幅图像共耗费4个多小时，而针对14×14尺寸的100幅图像进行重构，重构时间还不到原始尺寸下的25%，大幅度提高了计算方差过程中的运行效率。

另外，两种算法生成的MNIST干净样本在分类器上的分类正确率分别为86%和84%。由此可见，中心方差最小化算法相比总方差最小化算法在最后的准确率上略有降低，正确率的变化较小且在可接受的范围内，而效率的明显提升是本文算法带来的主要改进。

（2）结果与分析

使用FGSM、BIM、DeepFool以及C&W对抗样本算法来生成MNIST测试集，通过中心方差最小化将对抗样本进行重构，重构后的图像分类正确率如表2所示。由表2中数据可知，当全部使用对抗样本作为测试数据集时，整体正确率维持在68%～70%。中心总方差最小化对以上攻击能起到一定的防御作用。

3.2 图像缝合优化

（1）对抗样本图像重构

本文实验使用MNIST干净样本作为原始数据集，通过C&W攻击生成对抗样本，然后通过图像缝合优化的方式进行图像重构，经过处理后的图像如图5所示。

表2 中心方差最小化防御性能

图5 干净样本、对抗样本和缝合后样本（从左到右）

Figure 5 Clean samples, adversarial samples, and quilted samples (from left to right)

将对抗样本与重构后的图像对比，可发现两方面不同。一方面，整体图像上的噪声点消失。使用补丁块进行缝合后的图像中，由于补丁块均来源于干净样本，所以在重构后的图像中不包含噪声点。另一方面，重构后的图像在数字边缘锯齿更明显，相比原始图像造成了一定的改变，但仍能保持较好的相似性。

（2）防御性能测试

针对FGSM、BIM、DeepFool和C&W对抗样本攻击算法进行测试。为了保证图像缝合优化的防御方案不影响干净样本正常分类，本文实验中也对干净样本进行图像缝合操作，其防御性能如表3所示。

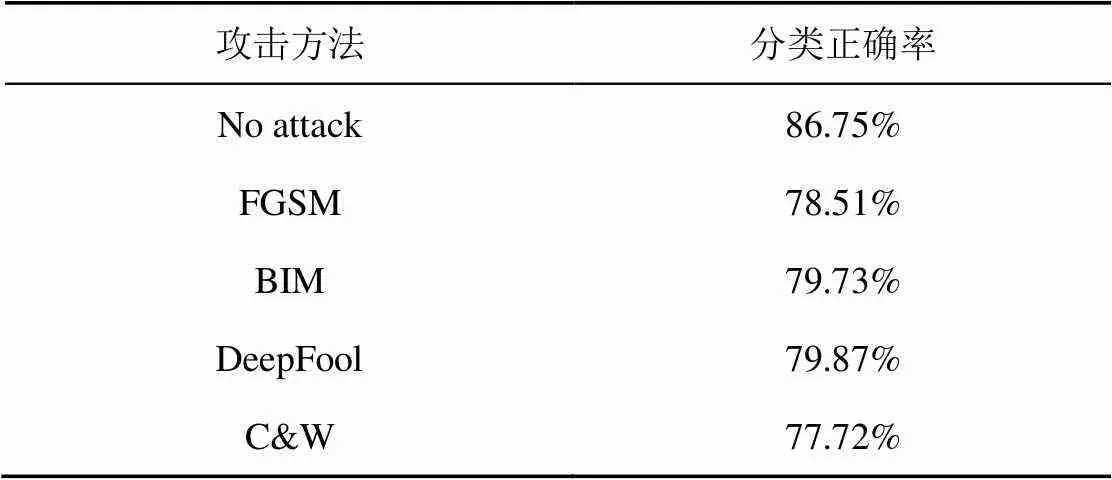
表3 图像缝合优化防御性能

由表3中数据可以看出，基于图像缝合优化的对抗样本防御方案在使用MNIST数据集的情况下有较好的防御效果，对于对抗样本重构后的图像能保持75%以上的分类正确率，防御效果良好。

3.3 对比分析

（1）图像重构算法对比

常见的图像变换算法还有图像裁剪与缩放、位深度压缩和JPEG压缩等，本文将以上3种图像变换算法作为对抗样本防御的方法进行测试，并将测试结果与本文提出的两种方法进行对比。5种图像重构算法的参数情况如表4所示。

表4 5种图像重构算法的参数情况

经过重构处理后的5种图像数据输入分类器，在该步骤中，不使用重构后的图像对分类器进行训练，保证分类器对于样本的分类能更接近干净样本。表5中展示了干净样本经过5种图像处理算法后的分类正确率。

表5 5种算法对干净样本分类的影响

由表5中数据可知，在干净样本作为数据集时，本文所提出的两种方法对干净样本的分类正确率维持在85%左右，对干净样本降低了一定的分类正确率，但仍然在可接受的范围内。其中，中心方差最小化算法重构图像耗费时间较长，重构10 000幅的防御效果和100幅没有明显区别，所以本文选取了100幅图像进行重构。

（2）对各种攻击的防御效果

在图6中，整体分为针对FGSM、BIM、DeepFool以及C&W这4种攻击算法的防御效果，每一部分从左到右依次是JPEG、中心方差最小化、位深度压缩、图像缝合优化、图像裁剪与缩放5种防御方式下对抗样本的分类正确率。

图6 5种图像重构算法对4种攻击算法的防御结果

Figure 6 Defense results of five image reconstruction algorithms against four attack algorithms

从最终的图像分类正确率上来看，最高的是图像缝合优化，对4种攻击算法的防御都达到了75%以上，其次是中心方差最小化，该算法对4种攻击的防御效果也比较均衡，基本维持在70%。而剩余3种图像重构算法则对不同攻击算法的表现不稳定，且整体分类正确率不足60%。本文提出的两种算法不依赖攻击方式，防御性能较好。需要指出的是，图像缝合优化防御效果比中心方差最小化好，前提条件是要先构建补丁库，需要较多的干净样本数据集，而中心方差最小化则不需要数据集，这是它的优势。

4 结束语

本文分别设计并实现了基于中心方差最小化的图像重构和基于图像缝合优化的图像重构两种算法。在基于中心方差最小化的图像重构中，针对MNIST图像的尺寸特点，采用图像的中心区域计算方差，以方差和最小化作为目标函数，对待测样本进行了图像重构；在图像缝合优化中，原算法所对应的图像需要有较大的尺寸，本文实验合理设计了补丁块的大小，并且将重叠区域纳入补丁块选取的考量中。本文的图像重构防御算法可进行一定修改用于其他图像数据集，有较好的通用性。本文通过实验说明了本文防御算法在不同对抗样本攻击算法中的防御效果，另外，将其他图像重构算法与本文算法进行比较，说明本文算法具有良好的防御性能。

[1] SIMONVAN K, ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[C]//Proceedings of 3rd International Conference on Learning Representations (ICLR 2015). 2015.

[2] EYKHOLT K, EVTIMOV I, FERNANDES E, et al. Robust physical-world attacks on deep learning visual classification[C]//Proceedings of 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). 2018.

[3] SZEGEDY C, ZAREMBA W, SUTSKEVER I, et al. Intriguing properties of neural networks[C]//Proceedings of 2nd International Conference on Learning Representations (ICLR 2014). 2014.

[4] SHARIF M, BHAGAVATULA S, BAUER L, et al. Accessorize to a crime: Real and stealthy attacks on state-of-the-art face recognition[C]//Proceedings of the 2016 ACM SIGSAC Conference. 2016.

[5] PRASAD A, SUGGALA A S, BALAKRISHNAN S, et al. Robust estimation via robust gradient estimation[J]. Journal of the Royal Statistical Society Series B, 2020, 82(3): 601-627.

[6] 宋蕾, 马春光, 段广晗. 机器学习安全及隐私保护研究进展[J]. 网络与信息安全学报, 2018, 4(8): 1-11.

SONG L, MA C G, DUAN G H. Machine learning security and privacy:a survey[J]. Chinese Journal of Network and Information Security, 2018, 4(8): 1-11.

[7] GOODFELLOW I J, SHLENS J, SZEGEDY C. Explaining and harnessing adversarial examples[C]//Proceedings of 3rd International Conference on Learning Representations (ICLR 2015). 2015.

[8] KURAKIN A, GOODFELLOW I J, BENGIO S. Adversarial examples in the physical world[C]//Proceedings of 5th International Conference on Learning Representations (ICLR 2017). 2017.

[9] MOOSAVI-DEZFOOLI S, FAWZI A, FROSSARD P. DeepFool: a simple and accurate method to fool deep neural networks[C]//Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition. 2016: 2574-2582.

[10] CARLINI N, WAGNER D. Towards evaluating the robustness of neural networks[C]//Proceedings of 2017 IEEE Symposium on Security and Privacy (SP). 2017.

[11] LECUN Y, BOTTOU L. Gradient-based learning applied to document recognition [C]//Proceedings of the IEEE. 1998: 2278-2324.

[12] SZEGEDY C, LIU W, JIA Y, et al. Going deeper with convolutions[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2015). 2015.

[13] 刘西蒙, 谢乐辉, 王耀鹏, 等. 深度学习中的对抗攻击与防御[J]. 网络与信息安全学报, 2020, 6(5): 36-53.

LIU X M, XIE L H, WANG Y P, et al. Adversarial at tacks and defenses in deep learning[J]. Chinese Journal of Network and Information Security, 2020, 6(5): 36-53.

[14] DZIUGAITE G K, GHAHRAMANI Z, ROY D M. A study of the effect of JPG compression on adversarial images[C]//Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). 2016.

[15] 严飞, 张铭伦, 张立强. 基于边界值不变量的对抗样本检测方法[J].网络与信息安全学报, 2020, 6(1): 38-45.

YAN F, ZHANG M L, ZHANG L Q. Adversarial examples detection method based on boundary values invariants[J]. Chinese Journal of Network and Information Security, 2020, 6(1): 38-45.

[16] LU J. No need to worry about adversarial examples in object detection in autonomous vehicles[EB].

[17] GUO C, RANA M, CISSE M, et al. Countering adversarial images using input transformations[C]//The 6th International Conference on Learning Representations (ICLR 2018). 2018.

[18] EFROS A A, FREEMAN W T. Image quilting for texture synthesis and transfer[C]//Proceedings of the ACM SIGGRAPH Conference on Computer Graphics. 2001: 341-346.

[19] BOYKOV Y, VEKSLER O, ZABIH R. Fast approximate energy minimization via graph cuts[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, 23(11): 1222-1239.

Adversarial example defense algorithm for MNIST based on image reconstruction

QIN Zhongyuan1, HE Zhaoxiang1, LI Tao1,2, CHEN Liquan1,2

1. School of Cyber Science and Engineering, Southeast University, Nanjing 211189, China 2. Network Communication and Security Purple Mountain Laboratory, Nanjing 211189, China

With the popularization of deep learning, more and more attention has been paid to its security issues. The adversarial sample is to add a small disturbance to the original image, which can cause the deep learning model to misclassify the image, which seriously affects the performance of deep learning technology. To address this challenge, the attack form and harm of the existing adversarial samples were analyzed. An adversarial examples defense method based on image reconstruction was proposed to effectively detect adversarial examples. The defense method used MNIST as the test data set. The core idea was image reconstruction, including central variance minimization and image quilting optimization. The central variance minimization was only processed for the central area of the image. The image quilting optimization incorporated the overlapping area into the patch block selection. Considered and took half the size of the patch as the overlap area. Using FGSM, BIM, DeepFool and C&W attack methods to generate adversarial samples to test the defense performance of the two methods, and compare with the existing three image reconstruction defense methods (cropping and scaling, bit depth compression and JPEG compression). The experimental results show that the central variance minimization and image quilting optimization algorithms proposed have a satisfied defense effect against the attacks of existing common adversarial samples. Image quilting optimization achieves over 75% classification accuracy for samples generated by the four attack algorithms, and the defense effect of minimizing central variance is around 70%. The three image reconstruction algorithms used for comparison have unstable defense effects on different attack algorithms, and the overall classification accuracy rate is less than 60%. The central variance minimization and image quilting optimization proposed achieve the purpose of effectively defending against adversarial samples. The experiments illustrate the defense effect of the proposed defense algorithm in different adversarial sample attack algorithms. The comparison between the reconstruction algorithm and the algorithm shows that the proposed scheme has good defense performance.

adversarial example, image reconstruction, deep learning, image classification

s: TheNational Key R&D Program of China (2020YFE0200600), The National Natural Science Foundation of China (61601113)

TP393

A

10.11959/j.issn.2096−109x.2021095

秦中元（1974−），男，河南安阳人，博士，东南大学副教授，主要研究方向为人工智能安全、无线网络安全。

贺兆祥（1995−），男，山东临沂人，东南大学硕士生，主要研究方向为人工智能安全、无线网络安全。

李涛（1984−），男，江苏镇江人，博士，东南大学副教授，主要研究方向为可信计算、移动终端安全、内生安全。

陈立全（1976−），男，广西玉林人，博士，东南大学教授、博士生导师，主要研究方向为移动信息安全、物联网系统与安全、云计算及大数据安全。

2021−06−01；

2021−09−14

秦中元，zyqin@seu.edu.cn

国家重点研发计划（2020YFE0200600）；国家自然科学基金（61601113）

秦中元, 贺兆祥, 李涛, 等. 基于图像重构的MNIST对抗样本防御算法[J]. 网络与信息安全学报, 2022, 8(1): 86-94.Citation Format: QIN Z Y, HE Z X, LI T, et al. Adversarial example defense algorithm for MNIST based on image reconstruction[J]. Chinese Journal of Network and Information Security, 2022, 8(1): 86-94.