使用EOF垂直基函数的像素基电离层层析重构

范玉荣 符杰林* 安 涛 王俊义 林基明

1(桂林电子科技大学认知无线电与信息处理教育部重点实验室 广西 桂林 541004)2(中国科学院上海天文台 上海 200030)3(广西高校卫星导航与位置感知重点实验室 广西 桂林 541004)

0 引 言

电离层是距离地面高度60～2 000 km的大气电离区域，其电子密度分布会影响无线电信号在电离层中的传播条件，因而电离层电子密度分布信息不仅对电离层物理具有重要意义，而且对星地通信和导航也具有重要意义[1]。使用GNSS观测数据和电离层层析技术对电离层进行三维建模，不仅克服了二维电离层模型的局限性，而且具有全天候观测、全球覆盖、低成本和高效率等优势[2]。

电离层层析成像是根据反演区域内的大量信号传播路径上的总电子含量来反演特定区域的电子密度分布[3]。其通常分为两类：函数基电离层层析和像素基电离层层析。函数基电离层模型采用一组函数来表示电离层电子密度分布，其优点在于可以用很少的参数即可表述区域内的电离层分布情况，但由于地面GNSS站的分布和卫星星座的几何特性，直接对观测资料进行求解往往十分困难[4]。对于像素基电离层层析，通常将反演区域划分为一系列格网并假定每个格网的电子密度为常数且均匀分布。然而，由于GNSS观测视角和地面测站数量及分布的限制，基于GNSS的像素基电离层层析通常存在数据不足而引起的不适定问题。为了解决不适定问题带来的影响，国内外众多学者先后提出了各种解决方法，文献[5]使用同时迭代算法(Simultaneous Iteration Reconstruction Technique，SIRT)进行电离层电子密度的重构，减小了噪声对解算结果的影响；Wen等[6]对代数重构(Algebraic reconstruction Technique，ART)算法松弛因子进行了改进，提出了IART算法；姚宜斌等[7]针对联合迭代重构算法迭代收敛慢且易受噪声影响的问题，利用上一轮迭代的电子密度反演结果，自适应地调整松弛因子和加权参数，提出了ASIRT算法；文献[8]提出的TV-MART算法，使用总变差(Total Variation，TV)最小化结合MART算法对电子密度进行重构，减小了由噪声引起的不稳定性；文献[9]对IART算法使用自搜索松弛因子改进，减小了由于松弛因子不合适而引起的误差；文献[10]将局部加权线性回归算法应用在电离层层析中，在一定程度上减弱了没有射线通过的格网对初始值的依赖。以上方法在一定程度上有效克服了重构过程中的不适定问题，提高了反演精度。但是，以上算法大多计算比较复杂，尤其在格网数目较大时，以上迭代算法会由于反演未知数过多和计算复杂的原因导致反演效率较低[11]，不便于实现电离层的实时预报预警研究。

本文通过从IRI2016中提取EOF垂直基函数，显著减少了未知数的个数，然后结合MART算法重构电离层电子密度，提高了反演效率，同时在一定程度上减小了不适定问题的影响。通过数值模拟仿真和实测数据实验结果表明该算法相对于传统层析算法在计算效率上有显著提升，同时在反演精度上也有一定的改进。

1 算法原理

本文算法在传统电离层层析成像的基础上，从IRI模型中提取垂直电子密度剖面获取EOF作为垂直方向的基函数。使用几个EOF的线性组合来表示每一个垂直电子密度剖面，从而将反演的未知数由每个格网的电子密度转变为垂直剖面的EOF系数，显著减少了需要反演的未知数。之后利用MART将重新构造的反演矩阵进行迭代计算得到EOF系数值，再结合EOF获得所有格网的电子密度。

1.1 电离层层析成像原理

电离层层析成像使用GPS射线的电离层斜向总电子含量(Slant Total Electron Content，STEC)重构电离层电子密度分布，其中STEC可以从双频GPS(Global Positioning System)接收机的伪距和载波相位观测值中提取出来，如式(1)所示，具体方法的详细描述见文献[12]。

(1)

式中：P4,sm是载波相位平滑伪距之后的观测值；c表示光速；DCBi和DCBj分别表示卫星和接收机的差分码偏差；f1和f2分别对应GNSS两个频点的频率。获得的STEC可以表示成电子密度沿信号路径上的积分，即：

(2)

式中：Ne为电子密度；l为信号路径；r为t时刻经度、纬度和高度所组成的位置向量；s为信号传播路径。将反演区域按照经度、纬度、高度方向上划分为三维格网，那么每条路径上的STEC测量值可以表示为：

(3)

式中：m为穿过电离层的射线总数；n为总格网数目；aij为第i条射线在第j个格网内的截距；xj为第j个格网的电子密度；ei为观测噪声和误差。如图1所示为电离层层析模型的简化示意图。

图1 电离层层析模型示意图

将式(3)写成矩阵形式可以表示为：

ym×1=Am×n·xn×1+em×1

(4)

式中：y表示GNSS信号射线传播路径上电离层STEC构成的m维列向量；A为GNSS信号射线穿过格网时的截距构成的m×n维投影矩阵，由于观测卫星数有限，其通常是一个稀疏矩阵；x为所有格网像素中心电子密度构成的n维列向量；e为噪声和观测误差构成的列向量。

1.2 EOF基函数

经验正交函数可以提取一组简化的变量来减少数据的维数，这些变量可以解释数据中的大部分特性[13]。因而原始数据可以表示为提取出的少量经验正交函数的线性组合，被广泛应用在气象和电离层数据分析和建模中。如施闯等[14]使用EOF和球谐函数分别作为垂直方向和水平方向基函数建立了3D电离层模型；Ansari等[15]使用EOF建立了韩国区域电离层总电子含量(Total Electron Content，TEC)模型。

为了获取电离层垂直剖面的EOF，通过IRI2016模型提取电子密度剖面矩阵，参数如表1所示。IRI2016模型是由空间研究协会(CORPAR)和国际无线电科学联盟(URSI)发起的经验电离层模型，其综合了全球范围内的电离层测高仪、散射雷达等电离层探测仪器的观测数据，因而在电离层建模中多使用其作为电离层背景模式。

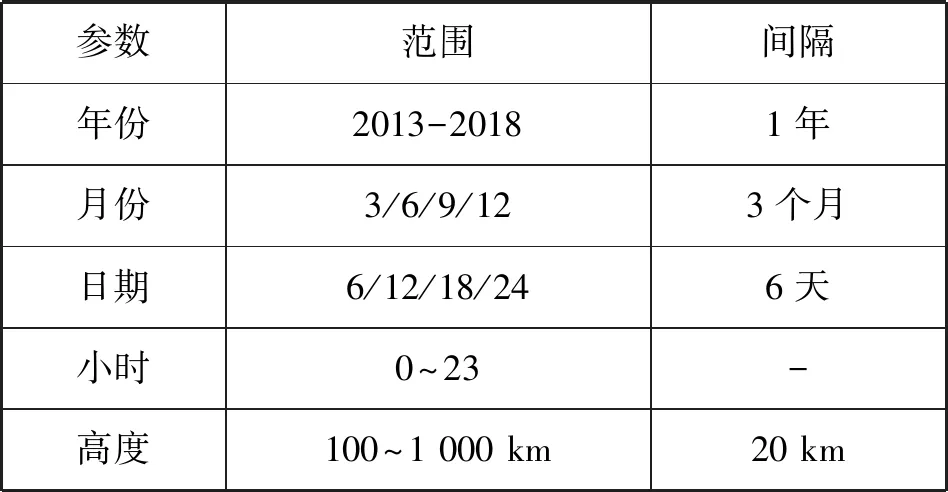
表1 从IRI2016获取电子密度剖面的参数范围

产生的电子密度剖面矩阵用Np×q表示，其中:p表示垂直像素个数；q表示从IRI2016中获取的电子密度垂直剖面数。通过对垂直剖面数据矩阵Np×q进行奇异值分解(SVD)，构造一组EOF基函数，具体如下：

(5)

式中：奇异值包含在对角矩阵S中；EOF基函数在矩阵U中。我们可以通过从奇异值中计算每个EOF的贡献百分比来选择占主导地位的EOF[15]。由于大部分情况下前三个EOF即可以代表96%以上的信息量，因而本文选取前三个占比较大的EOF。图2为UT02:00时刻的EOF示意图。

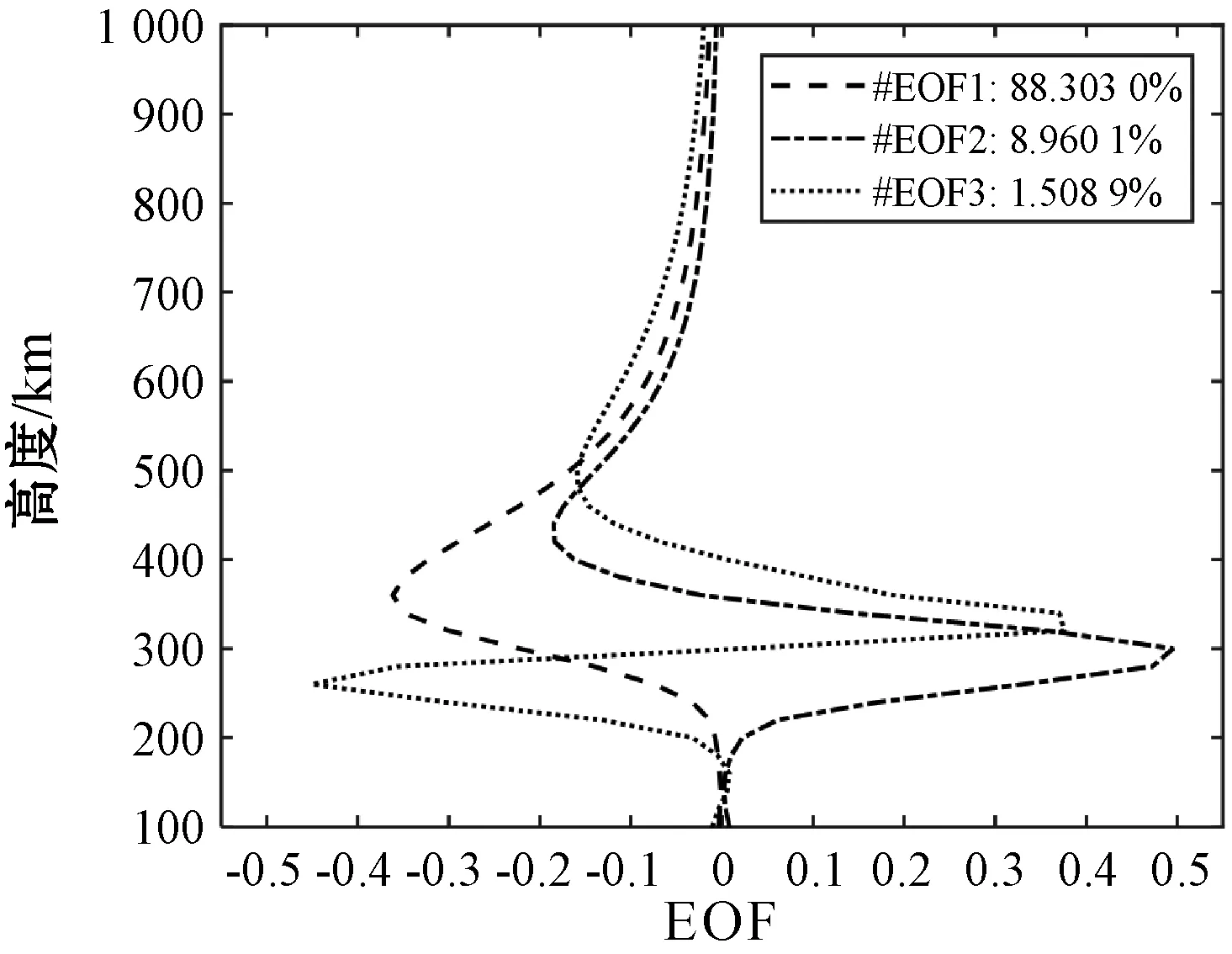
图2 UT02:00时刻的前三个EOF

这三个EOF可以构成矩阵Ep×3，那么对于反演区域内任一垂直剖面的电子密度都可以用EOF来线性表示。

1.3 EOF垂直基函数与MART结合

MART由于其迭代速度较快且可以克服反演值为负的问题，因而在电离层层析中被广泛使用。MART反演迭代公式如下：

(6)

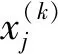
式(3)可以用EOF基函数表示为：

(7)

式中：Fn×c是由Ep×3按照对角组合得到的，其扩展方法如下：

(8)

式中：n为格网总数；c为每个剖面对应的EOF系数个数。式(8)可以进一步写为：

Hm×c·Yc×1=ym×1

(9)

值得注意的是，由于EOF有负数值，为防止迭代过程中解发散的问题，对Hij做了绝对值处理，因而最终的反演迭代公式为：

(10)

2 实验与结果分析

2.1 数值模拟实验

由于对全部反演区域真实的电离层状态未知，直接使用实测数据进行电离层电子密度反演无法全面地评判算法的有效性和稳定性，因而本文设计了数值模拟实验以验证算法的有效性和稳定性。选取的反演区域为35°N至55°N和5°W至25°E，高度范围为100至1 000 km。在纬度、经度和高度上的空间分辨率分别取2°、2°、20 km。选取2018年3月20日欧洲地区45个IGS观测站的GPS双频观测数据进行建模。具体观测站的选取和分布如图3所示，其中三角形标志为PQ052电离层测高仪观测站的位置。在实验过程中，使用10 min GPS观测数据进行实验，测站和卫星位置均取真实值。

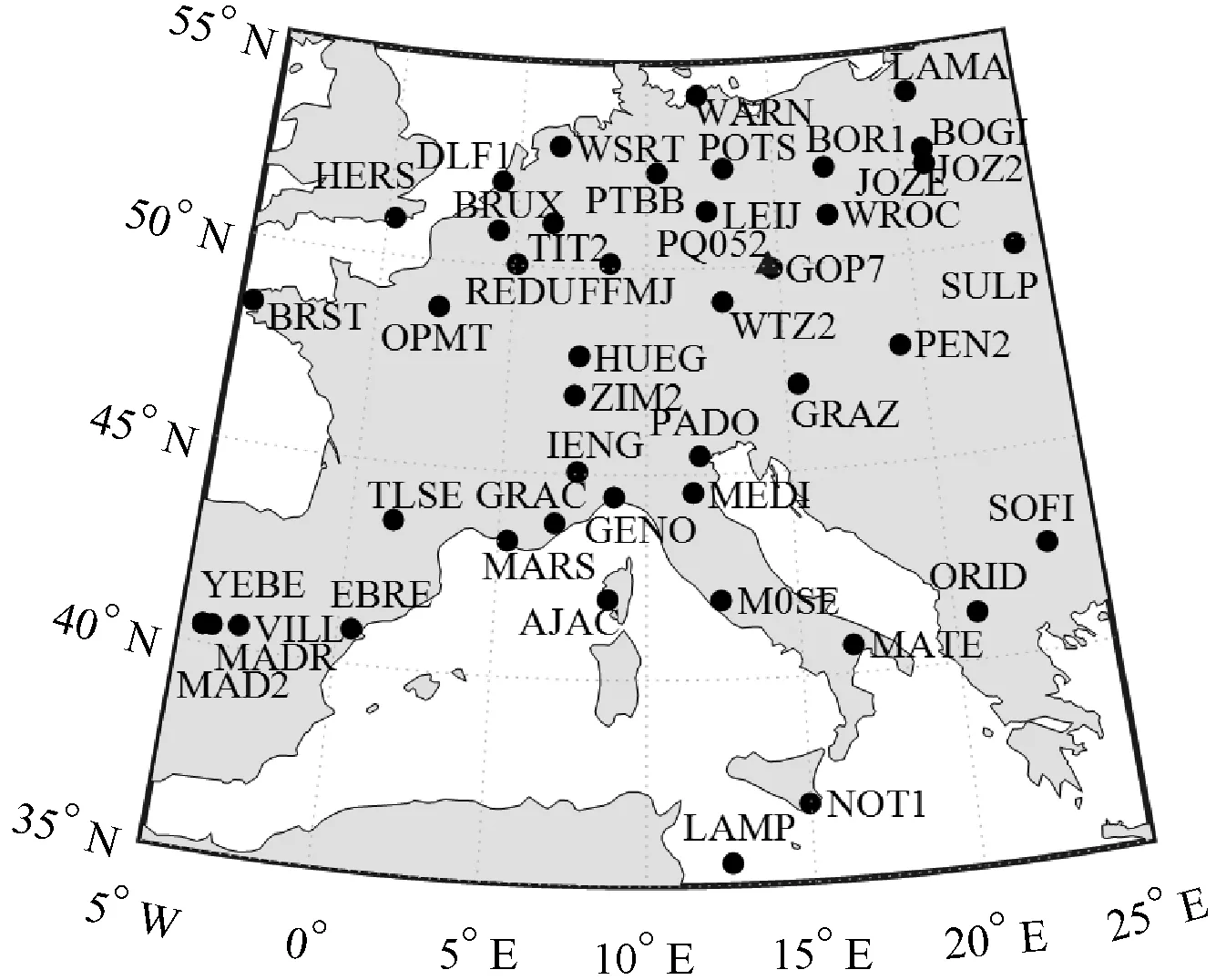
图3 IGS站点及测高仪观测站位置分布图

根据卫星位置和观测站位置计算射线在每个格网中的截距并构成式(4)中的投影矩阵A。考虑到EOF是由IRI模型中获取得到的，因而本文设置的真实电子密度为IRI2016的基础上添加一定的偏移量，如式(11)所示；同时在模拟STEC数据上增加了最大为1.5TECu(total electron content unit)的噪声；此外，初始电子密度设为xIRI。

(11)

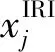
(12)

(13)

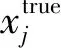
图4中(a)、(b)和(c)分别是UT07:00、UT12:00和UT19:00三个时刻两种算法解算结果在(51°N,11°E)处的电子密度剖面对比图。可以看出，在高度小于200 km的区域，MART反演结果比使用EOF基函数的反演结果要更加接近真实值，而在高度高于200 km的区域则反之。此外，表2给出了以上三个时刻两种算法的均方根误差和平均电子密度误差，可以看出，两种算法反演得到的电离层电子密度都比较接近真实值，在电子密度较大的时候反演误差也随之增大，但都远小于此时的电子密度峰值。总体来看，使用EOF基函数的算法相较于MART在精度上有一定提升。

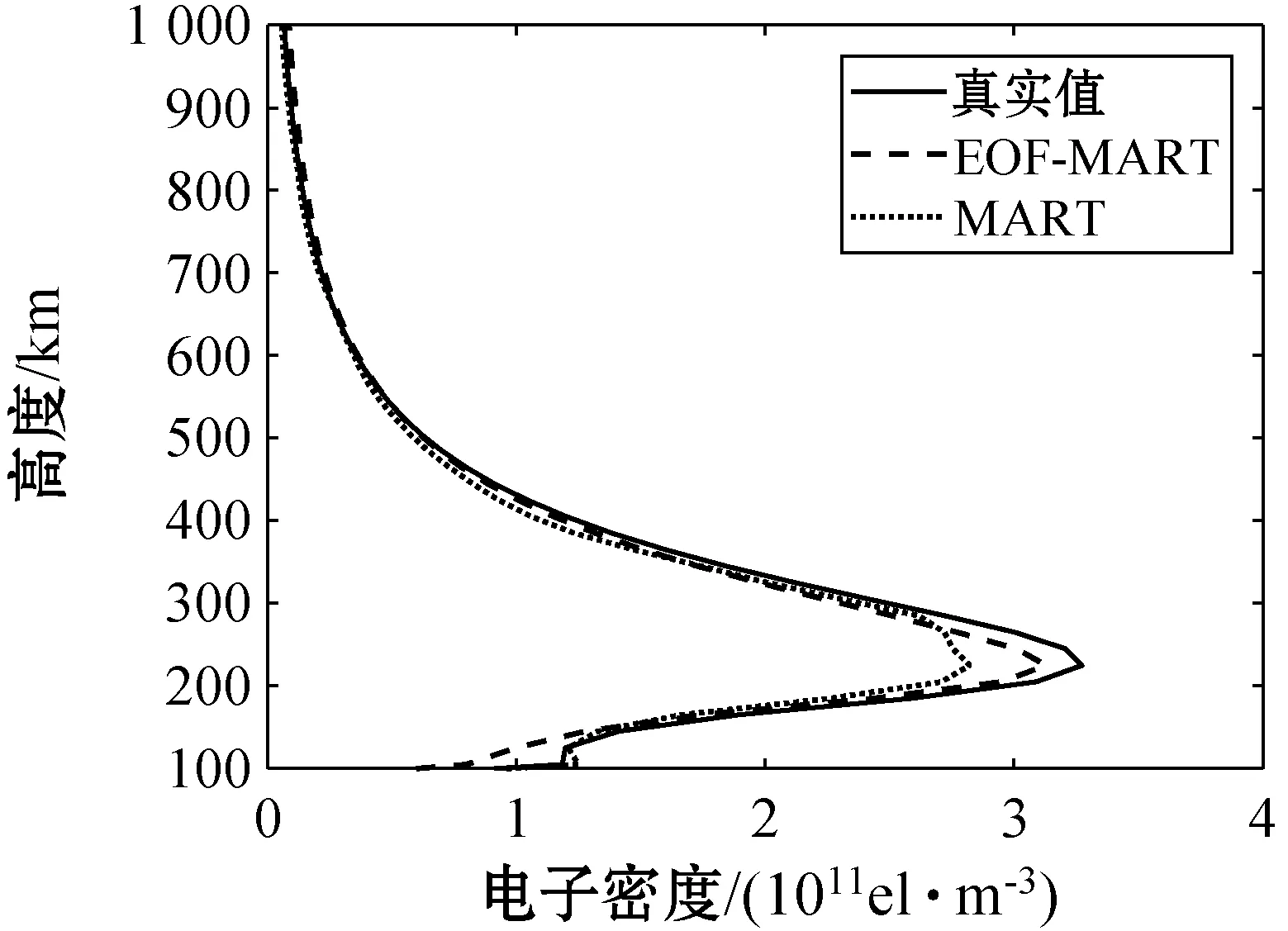
(a) UT07:00

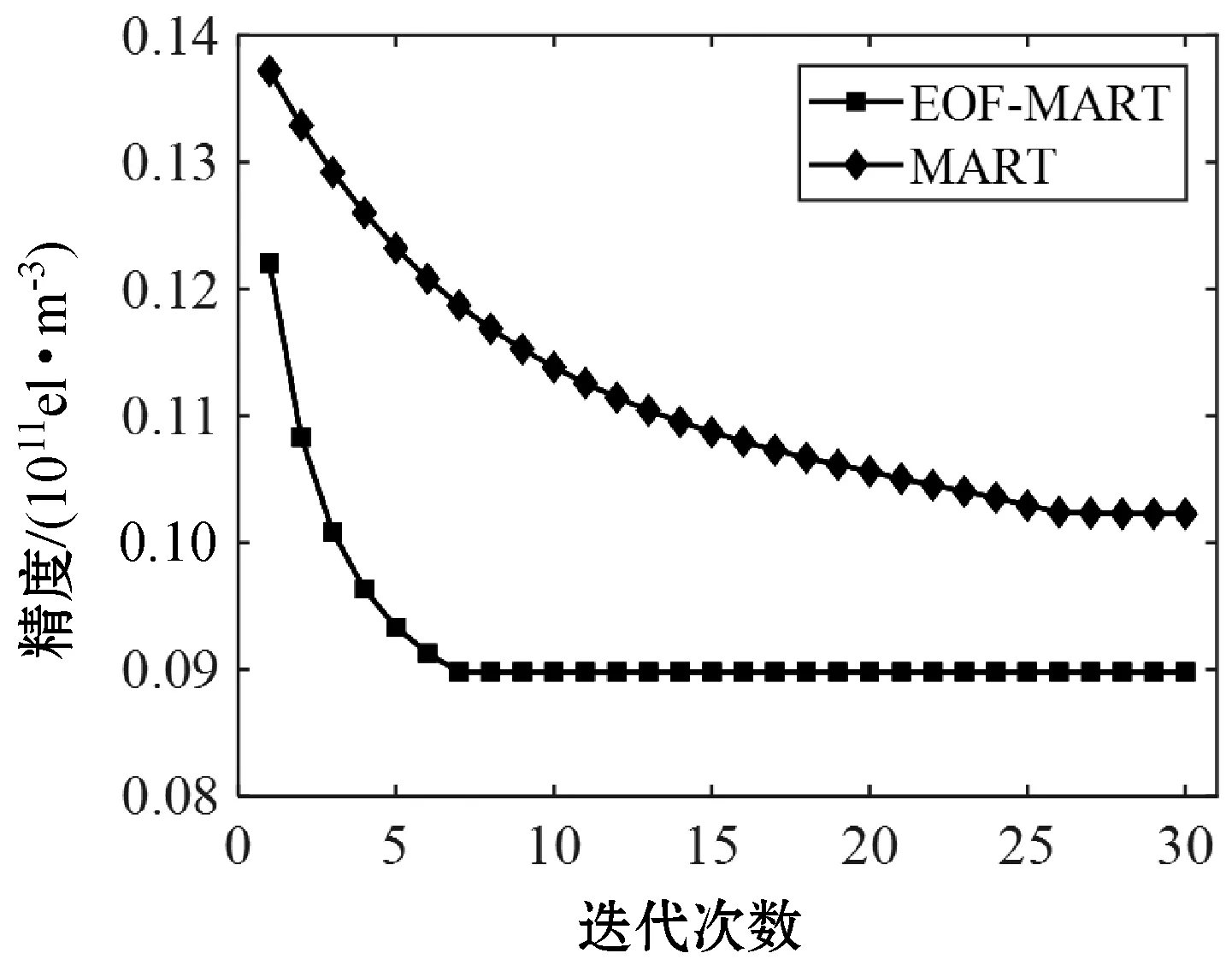
图5 两种算法的迭代次数与精度对比

(a) UT05:00

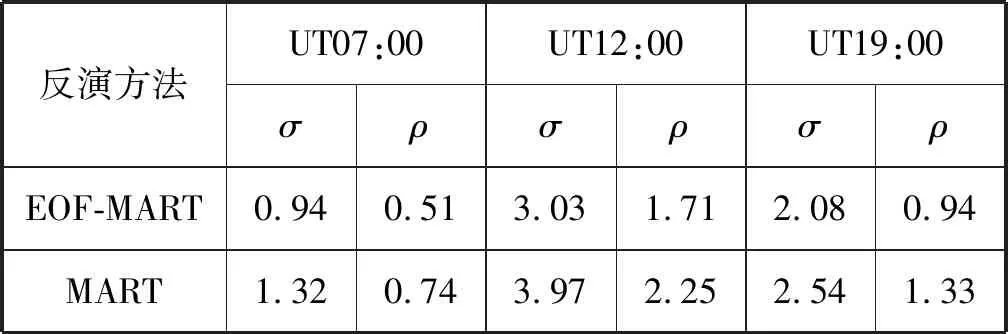
表2 两种算法反演精度对比

在实验中，使用MART算法，需要反演的未知数个数为6 750个，而通过使用EOF作为垂直基函数，其需要反演的未知数个数只有450个，显著减少了反演未知数个数，大大加快了反演速度。图5是UT02:00时刻两种算法的迭代次数与精度对比。可以看出，采用EOF作为垂直基函数，迭代7次左右就已经达到收敛，而传统MART算法则需要25次左右才达到收敛，且使用EOF作为垂直基函数的算法精度更高。这是因为采用EOF作为垂直基函数，当垂直方向的一系列格网中格网电子密度有修正时，可以带动整条垂直方向的格网都进行修正，从而收敛速度更快。这也证实了使用EOF作为垂直基函数的算法在计算效率上的优越性。

2.2 实测数据实验

为进一步评估使用EOF作为基函数反演电离层电子密度的精度，使用2018年3月20日欧洲地区45个IGS观测站的实际GPS双频观测数据获取STEC观测值进行计算。反演区域和格网划分与上述模拟实验一致。利用反演区域内电离层测高仪PQ052(50°N，14.6°E)的观测数据对反演结果进行核验。

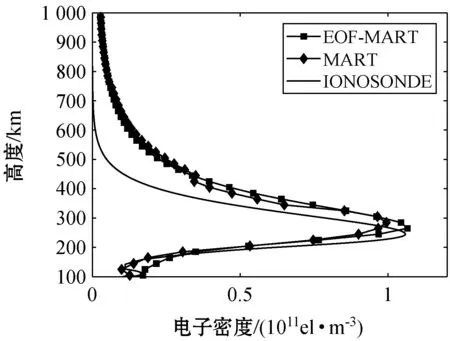
图6给出了UT05:00、UT11:00和UT19:00三个时刻两种算法反演得到的电离层电子密度剖面与测高仪观测数据的对比。从比较结果来看，使用EOF作为垂直基函数的算法的反演结果与测高仪观测数据更为接近。说明使用EOF作为垂直基函数的算法的精度相较于传统MART反演算法确实有一定提升。但是，两种算法在电子密度峰值高度上均与测高仪观测值存在一定差异，一方面是由于采用的GPS射线仰角较高而导致的垂直方向分辨率不高，另一方面是由于采用的EOF来源于IRI2016，因而反演得到的电子密度峰值高度与IRI2016接近。

图7是一天内UT 01:00至UT23:00各个时刻两种算法反演得到的电子密度的F2层峰值电子密度(NmF2)与测高仪观测值的对比。可以看出，两种算法反演获得的NmF2与测高仪观测数据总体上符合都较好，体现了电离层一天内的峰值电子密度随着时间推移先增大后逐渐减少的特性。大部分情况下，使用EOF垂直基函数的算法更接近测高仪观测结果。

图7 两种算法反演得到的NmF2与测高仪结果的对比

3 结 语

本文采用从IRI中提取出的EOF作为垂直基函数，结合MART算法实现对电离层电子密度进行快速精确层析反演。不同于传统电离层层析方法中将格网电子密度作为未知数反演，本文算法采用EOF作为垂直方向基函数，将EOF系数作为反演未知数，显著提高了反演效率，解决了传统方法中由于未知数数目较多而导致的反演效率低的问题。使用欧洲地区45个观测站10 min内GPS数据对电离层进行了建模实验。通过模拟数据实验和实测数据实验表明，相对于传统MART反演算法，本文算法在反演效率和精度上都有所提升。