船舶微电网源-荷级联系统母线电压振荡有源阻尼抑制策略

张勤进，郑祥鲁，刘彦呈，曾宇基

（大连海事大学轮机工程学院，大连 116026）

随着光伏、燃料电池等可再生能源以及电力电子技术的飞速发展，新能源全电推进船舶受到越来越多的关注[1]。作为新能源发电的有效形式，直流微电网以其较高的效率、模块化和高可靠性等优势逐步应用于新能源全电推进船舶[2]。

船舶直流微电网中源侧储能单元和负荷构成了源-荷级联系统[3]，主要有逆变器-电机交流负荷和DC-DC变换器-电阻直流负荷，逆变器及变换器紧密、快速的闭环控制使其呈现为恒功率负载CPL（constant power load）。恒功率负载具有负阻抗特性，该特性与滤波元件间的相互作用会严重危害源-荷级联系统的稳定性[4]。为了消除电力电子变换器高频开关产生的谐波电流和电磁干扰，通常在直流母线和恒功率负载之间加入一个LC输入滤波器，若滤波器没有足够的阻尼，会使得系统趋于不稳定，而且CPL的负阻抗特性会放大这种不稳定，引起直流母线电压振荡[5]。直流母线电压的稳定性是目前船舶供电系统的一项重要指标，若母线电压不稳定将会造成保护设备误动作或者引起用电设备损坏，进而影响船舶的安全运行。因此，维持直流母线电压稳定是船舶安全、稳定运行的关键[6]。所以针对船舶直流母线电压振荡问题的研究非常重要，具有较高实用价值。

目前，解决直流母线电压谐振问题的方法主要分为无源阻尼法和有源阻尼法两类。无源阻尼法主要针对LC输入滤波器和CPL组成的系统，通过在滤波器添加阻尼电阻或增加滤波器电容来解决CPL不稳定问题。文献[7]利用3种无源阻尼电路减小LC滤波器输出阻抗来稳定级联系统。文献[8]通过在直流母线上添加阻容电路，增加系统阻尼来抑制母线电压振荡。但无源阻尼法引入的阻尼器增加了系统体积和质量，造成系统能量损失。文献[9]通过在CPL侧加入电压环前馈回路的方式，构造出与CPL相并联的虚拟阻抗，达到修改CPL输入阻抗，进而稳定系统的目的。文献[10]通过并联虚拟阻抗和串联虚拟阻抗两种方式调节CPL的输入阻抗，满足阻抗比判据来消除级联系统的母线电压振荡。文献[11]通过一种前馈控制技术在CPL的输入端产生一个虚拟RC阻抗来抵消其负阻抗特性，此时CPL对外表现为正阻抗特性，避免了级联系统母线电压的振荡。文献[12]通过在电流环引入二阶低通滤波器的方式产生阻尼电流，抵消了CPL的负阻抗特性，消除了级联系统的母线电压振荡。上述几种方法都需要注入能量到负载侧，额外的能量将会影响负载性能，使得负载的动态特性变差。文献[13-14]则提出了通过降低源侧变换器输出阻抗的有源阻尼方法，来达到稳定级联系统的目的，但CPL前端没有加LC输入滤波器，研究对象不是带LC输入滤波器的源-荷级联系统。

综上所述，本文在考虑船舶直流微电网实际结构的基础上，针对由源测Boost变换器、LC输入滤波器和恒功率负载构成的源-荷级联系统的母线电压振荡问题，提出了一种基于虚拟负电感的有源阻尼稳定策略。首先分析了源-荷级联系统母线电压振荡的机理，通过源-荷级联系统的简化模型，推导出级联系统的稳定性约束条件，阐述了虚拟负电感稳定策略的基本原理。为了摆脱虚拟负电感策略对输出电流传感器较强的依赖性，进一步提出了利用非线性扰动观测器NDO（nonlinear disturbance observer）来估计输出电流的方法。最后，通过系统阻抗最小环路增益的奈奎斯特图进行了稳定性分析，并利用仿真实验验证控制策略的有效性。

1 源-荷级联系统母线电压谐振机理分析

典型船舶直流微电网系统结构如图1所示，系统由柴油发电机、光伏电池发电单元，蓄电池储能单元、阻性及CPL、岸电等部分组成。

图1 船舶直流微电网结构Fig.1 Structure of ship DC microgrid

如图1所示，若多个并联运行的储能及发电单元以相同的下垂系数运行，有利于系统的稳定运行。因此，对于所研究的船舶直流微电网系统而言，最不稳定的情况将是单个母线调压单元的运行模式，即级联运行模式。

船舶直流微电网源-荷级联系统等效电路如图2所示。源测Boost升压变换器工作在电压调节模式，负荷侧推进器及通导设备由电力电子变换器进行闭环控制，其瞬时输入功率恒定，等效为CPL。电路主要参数如表1所示。

图2 船舶微网源-荷级联系统等效电路Fig.2 Equiralent circuit of source-load cascade system of ship microgrid

表1 电路主要参数Tab.1 Main circuit parameters

1.1 恒功率负载的负阻抗特性与能量回馈作用

根据恒功率负载的功率和电压关系，可得

式中：PCPL、iCPL分别为恒功率负载功率和电流；vf为滤波电容电压即恒功率负载端电压。

取一稳态工作点(ICPL=PCPL/Uf)，求其偏导数可得电流随电压的变化率为

进而在给定工作点，恒功率负载的I-V线可以用与曲线相切的直线方程表示为

式中，Uf、ΔUf分别为恒功率负载的稳态电压和电压变化率。

根据式（3）可以得到恒功率负载的等效负阻抗及等效电流源为

式中：ΔRCPL为恒功率负载的负阻抗；为稳态电阻。由式（4）知恒功率负载具有负阻抗特性，该特性会减小系统阻尼，使得系统稳定性降低。

式中，ΔP为恒功率负载回馈到源侧的能量。正稳态电阻具有消耗电能转化为热能的作用，对源变换器产生正阻尼作用，使得输出电压收敛；而负增量阻抗的能量回馈作用，对源变换器产生负阻尼作用，造成输出电压发散，易发生母线电压振荡。

1.2 LC滤波器低阻尼振荡

由图2可推出LC输入滤波器的输出阻抗为

式中，s为拉普拉斯算子。

由前述可知恒功率负载具有负增量阻抗ΔRCPL，该特性会减小LC输入滤波器的阻尼，得到

由式（9）可知，恒功率负载的负增量阻抗减小了LC输入滤波器的阻尼，增加了LC滤波器低阻尼振荡及直流母线电压失稳可能性，且随着恒功率负载的增加，滤波器阻尼系数逐渐减小。

因此，当恒功率负载的功率达到一定值时，LC滤波器的阻尼不足以维持直流母线电压恒定，将会发生等幅度振荡。起始振荡频率近似于LC输入滤波器自身的振荡频率[1]。

可求得母线电压起始振荡频率在340 Hz左右。

2 基于NDO的虚拟负电感稳定策略

为解决源-荷级联系统母线电压振荡问题，提出了基于NDO的虚拟负电感有源阻尼稳定策略，通过在下垂控制环添加虚拟负电感的方式，抵消了LC滤波器较大的电感值，抑制了直流母线电压谐振。船舶直流微网源-荷级联系统简化电路如图3所示。

图3 源-荷级联系统简化等效电路Fig.3 Simplified equivalent circuit of source-load cascade system

为得到源测变换器的输出阻抗Zo，建立源侧Boost变换器的小信号模型如图4所示。

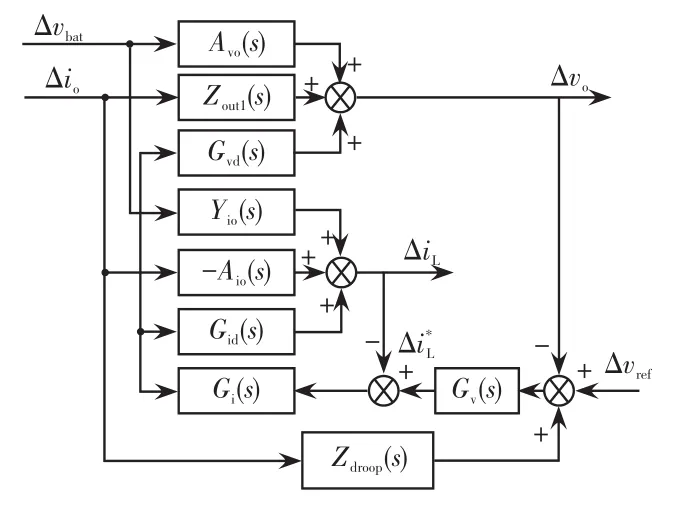
图4 Boost变换器小信号模型Fig.4 Small signal model of Boost converter

图4中：

式中，D为占空比。

由式（11）～（17）及图4得到变换器闭环输出阻抗为

2.1 虚拟负电感控制策略

由图3得源-荷级联系统等效电路的输出阻抗为

为确保级联系统渐近稳定，总阻抗Z(s)不应有右半平面极点，根据劳斯稳定性判据，需要满足

根据式（19）、（20）和（21）可得

由式（22）可知，滤波电容Cf的增大以及滤波电感Lf的减小使得系统带恒功率负载能力增强，有利于级联系统的稳定。然而，滤波电容的增大会导致系统体积加大，滤波电感也不容易直接修改。

因此，提出了一种虚拟负电感的有源阻尼方法，利用虚拟负电感抵消较大的滤波电感，来提高系统带恒功率负载的能力。虚拟负电感结构如图5所示。

由图5可知，虚拟负电感-Ldroop将抵消部分滤波电感值Lf。根据式（22）可知，滤波电感的减小可以增加系统带恒功率负载的能力，从而提高系统的稳定裕度。

图5 虚拟负电感策略Fig.5 Virtual negative inductance strategy

虚拟负电感将通过下垂控制环路建立在源端变换器的输出侧，通过修改下垂系数实现，即

式中：Rdroop为下垂系数；-Ldroop为虚拟负电感。

由式（23）可知，所提稳定策略的下垂环路中存在一个纯微分算子，这可能会给系统带来高频噪声。为了滤除高频噪声，添加了一阶低通滤波器。修正后的下垂系数可以表示为

式中，ω0为低通滤波器的截止频率，此处取为LC输入滤波器的谐振频率2 132 rad/s。

所提出的虚拟负电感稳定控制器接收输出电流传感器的值，得到输出电压的参考值为

图6 虚拟负电感控制级联系统结构Fig.6 Structure of cascade system under virtual negative inductance control

2.2 非线性扰动观测器设计

从图6及式（25）可以看出，要实现提出的虚拟负电感稳定策略，需要准确测量前级Boost变换器的输出电流io。因此，控制策略的可靠性将在很大程度上取决于输出电流传感器。若传感器发生故障，提出的虚拟负电感策略将无法实施。为解决电流传感器可能出现的故障问题，进一步设计了基于Boost变换器的非线性扰动观测器来估计输出电流值，摆脱虚拟负电感控制策略对输出电流传感器较强的依赖性。观测器设计步骤如下。

源侧Boost变换器工作在连续导电模式CCM（continuous conduction mode），其平均数学模型为

式中：vbat为输入侧电压；iL为电感电流；vo为输出电压；L1、R1分别为Boost变换器的电感及其寄生电阻；d为平均占空比；Co、io分别为输出电容和输出电流。

由源侧Boost变换器平均数学模型转换为标准的非线性形式为

式中：x为状态变量；x1为电感电流；x2为输出电压vo；u为输入信号；w为要估计的扰动信号。

定义 f(x)为系统方程，g1(x)为输入通道函数，g2(x)为扰动通道函数，即

根据文献[16]可以得到非线性扰动观测器函数表达式为

观测器的估计误差是观测器性能好坏的重要指标，其表达式为

由式（33）可看出l2(x)与观测器估计误差相关，而l1(x)对观测器的估计误差没有影响。为简化观测器表达式，此处l1(x)置为零。当扰动观测器参数满足：

即满足两个条件：一是扰动观测器的增益l2(x)小于零；二是扰动信号在时间趋于无穷时近似为一个常数时，式（33）中扰动观测器的动态估计误差存在一个渐进稳定点，此时估计的输出电流会收敛到实际的输出电流值。

微课是最近流行的多媒体电教手段之一。微课以它的信息容量大，可操作性强的特点，在美术课教学中既激发了学生的学习兴趣，调动了学习的积极性，又给学生练习提供了广泛的可以参考的信息资料，开阔了学生的眼界，拓宽了学生的思维，培养了学生的创新意识。

由式（31）和（34）可得观测器增益l2(x)为

根据式（27）、（30）、（31）和（35），得到非线性扰动观测器表达式如下：

扰动观测器可以观测出Boost变换器的输出电流值，摆脱了虚拟负电感控制策略对输出电流传感器较强的依赖性。在输出电流传感器发生故障时，也能够利用观测器的估计值正常工作，保障了系统在突发情况下的稳定运行。其系统控制结构如图7所示。

图7 基于NDO的虚拟负电感控制结构Fig.7 Structure of virtual negative inductance control based on NDO

3 稳定性分析

为了验证所提虚拟负电感控制策略的有效性，详细推导了系统的小回路增益Tm，用奈奎斯特稳定性判据分析了CPL功率变化、下垂系数变化以及LC输入滤波器电容变化对系统稳定性的影响。为了得到系统的小回路增益，详细分析了前级Boost变换器和恒功率负载的阻抗模型，如图8所示。

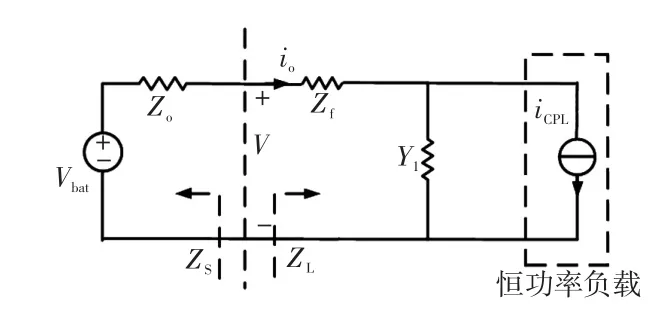
图8 级联系统阻抗模型Fig.8 Iimpedance model of cascade system

3.1 系统最小回路增益

图8中Zo是源侧输出阻抗，Zf是滤波器电感及其寄生电阻，Y1是恒功率负载与滤波器电容的并联输入导纳。

若系统表达式（39）没有右半平面极点（RHZ），则整个系统稳定。同样若分母D(s)没有右半平面零点（RHP），系统也稳定。由自动控制理论可知式（42）中RHZ数量可以通过奈奎斯特轨迹环绕（-1，0）的次数决定。

式中，N(0,0)和N(-1,0)分别为奈奎斯特轨迹顺时针环绕（0，0）和（-1，0）的次数。由于原系统的电源侧和负荷侧都是设计独自稳定，所以RHP(1+ZSYL)为零。

由式（11）～（16）、（24）及图4可得源侧Boost变换器施加控制算法后的闭环输出阻抗为

3.2 奈奎斯特稳定性分析

3.2.1 CPL功率变化

在这一部分，研究了恒功率负载功率变化对系统稳定性的影响，并且以传统下垂控制方法作对比。如图9所示，二者对比试验下垂系数设置完全相同，为0.3。虚拟负电感设置为-0.4 mH，低通滤波器截止频率为2 132 rad/s。设置了3个恒功率负载参数分别为0.9 kW、1.9 kW和2.9 kW。其他参数如表1所示。

图9 恒功率负载变化时奈奎斯特图Fig.9 Nyquist diagram with variation in CPL

如图9（a）所示，当CPL功率为0.9 kW时，奈奎斯特轨迹不包围临界点（-1，0），表明在传统下垂控制下系统是稳定的。然而，当CPL的功率为1.9 kW时，奈奎斯特轨迹越过临界点（-1，0）。此时，任何系统参数变化或外部干扰都可能使奈奎斯特轨迹包围点（-1，0），导致系统不稳定。因此，1.9 kW是传统下垂控制系统的临界稳定功率。当CPL的功率为2.9 kW时，奈奎斯特轨迹包围临界点（-1，0），系统不稳定。

图9（b）为施加虚拟负电感稳定策略后的奈奎斯特图。施加控制算法后的奈奎斯特轨迹都没有环绕点（-1，0），系统在CPL功率为0.9 kW、1.9 kW和2.9 kW时都保持稳定。此外，与传统下垂控制相比，其奈奎斯特轨迹的稳定裕度明显提高，这进一步证实了所提出的稳定策略在CPL功率变化时具有较高的鲁棒性。

3.2.2 下垂系数变化

在这一部分，研究了下垂系数变化对级联系统稳定性的影响。在船舶直流微网多源并联运行时，需要设计合适的下垂系数使得系统功率分配精度和稳定性达到一个最佳运行点。在系统运行期间下垂系数可能是变化的，因此需要分析变下垂系数对系统稳定性的影响。此处为简化分析，讨论了下垂系数在单台设备运行时，对系统稳定性的影响。考虑了系统在下垂系数为0.3、0.5和0.7，CPL功率为1.2 kW时的稳定性，其他参数如表1所示。

如图10（a）所示，随着下垂系数的增大，系统的稳定性逐渐降低。下垂系数为0.3时，奈奎斯特轨迹不包围点（-1，0），此时系统保持稳定。然而，当下垂系数为0.5和0.7时，其奈奎斯特轨迹包围点（-1，0），系统此时不稳定。

图10（b）为施加虚拟负电感稳定策略后的奈奎斯特图。3个下垂系数对应的奈奎斯特轨迹都没有包围点（-1，0），系统始终保持稳定。由图10可知，与传统的下垂控制系统相比，所提出的虚拟负电感稳定策略在下垂系数变化时具有较好的鲁棒性。

图10 下垂系数变化时奈奎斯特图Fig.10 Nyquist diagram with variation in droop coefficient

3.2.3 LC滤波器电容变化

在所研究的船舶源-荷级联中，为了获得造成噪声较小且稳定的直流母线电压，LC滤波器普遍采用容值较大的电解电容器，但其具有串联电阻大、损耗高及高频特性差等缺点。采用小容量薄膜电容器取代电解电容，可以避免出现上述问题。但根据前述公式推导可知，滤波器电容减小会导致系统的稳定性降低，系统带恒功率负载的能力减弱。所以，需要分析LC滤波器电容变化对系统稳定性的影响。分析了滤波电容为2 200 μF、1 000 μF和500 μF，CPL功率为2 kW时系统的稳定性，其他参数如表1所示。

如图11（a）所示，在传统下垂控制下，当滤波电容为2 200 μF时，奈奎斯特轨迹不包围点（-1，0），此时系统保持稳定运行。当滤波器电容值为1 000 μF、500 μF时，其奈奎斯特轨迹包围点（-1，0），此时系统不稳定。可以看出，随着LC滤波器电容值的减小，系统的稳定性逐渐降低。

图11 输出电容变化时奈奎斯特图Fig.11 Nyquist diagram with variation in output capacitance

图11（b）为施加虚拟负电感稳定策略后的奈奎斯特图。3个不同滤波电容值的奈奎斯特轨迹都没有包围点（-1，0），系统始终保持稳定。与传统的下垂控制相比，提出的虚拟负电感控制策略具有良好的鲁棒性，提高了系统的稳定裕度。

4 仿真分析

为了验证所提虚拟负电感控制策略的有效性，在Matlab/Simulink搭建了由源测Boost变换器、LC滤波器和恒功率负载组成的级联系统仿真模型。通过3个仿真实例的比较，验证了奈奎斯特稳定性分析部分的结论，分析了3个参数对母线电压稳定性的影响。

4.1 恒功率负载变化

第一种情形，验证所提控制算法在抑制由恒功率负载引起母线电压振荡的有效性。如图12所示。

图12 算法施加前后的母线电压Fig.12 Bus voltage before and after the application of algorithm

在1 s之前，恒功率负载为0.9 kW，母线电压稳定。在1 s恒功率负载增加至2 kW，母线电压失稳且以固定频率等幅振荡。在2.5 s施加虚拟负电感稳定策略，母线电压在10 ms内恢复到新的稳定状态。在0.5 s去除虚拟负电感稳定策略，母线电压再次失稳振荡。因此，所提出的虚拟负电感控制策略对恒功率负载造成的母线电压振荡具有较好的抑制作用。

为了验证恒功率负载功率大小和母线电压振荡之间的关系，进一步通过仿真实验得到了系统母线电压在恒功率负载为2 kW、3 kW、4 kW、5 kW时的波形，如图13所示。

从图13可以看出，随着恒功率负载的增加，其母线电压振荡的幅度逐渐加大，恒功率负载大小与母线电压振荡幅度成正比。为了分析恒功率负载功率和母线电压振荡频率之间的关系，给出母线电压振荡的局部分析，如图14所示。

图13 变恒功率负载功率时母线电压Fig.13 Bus voltage with variable CPL

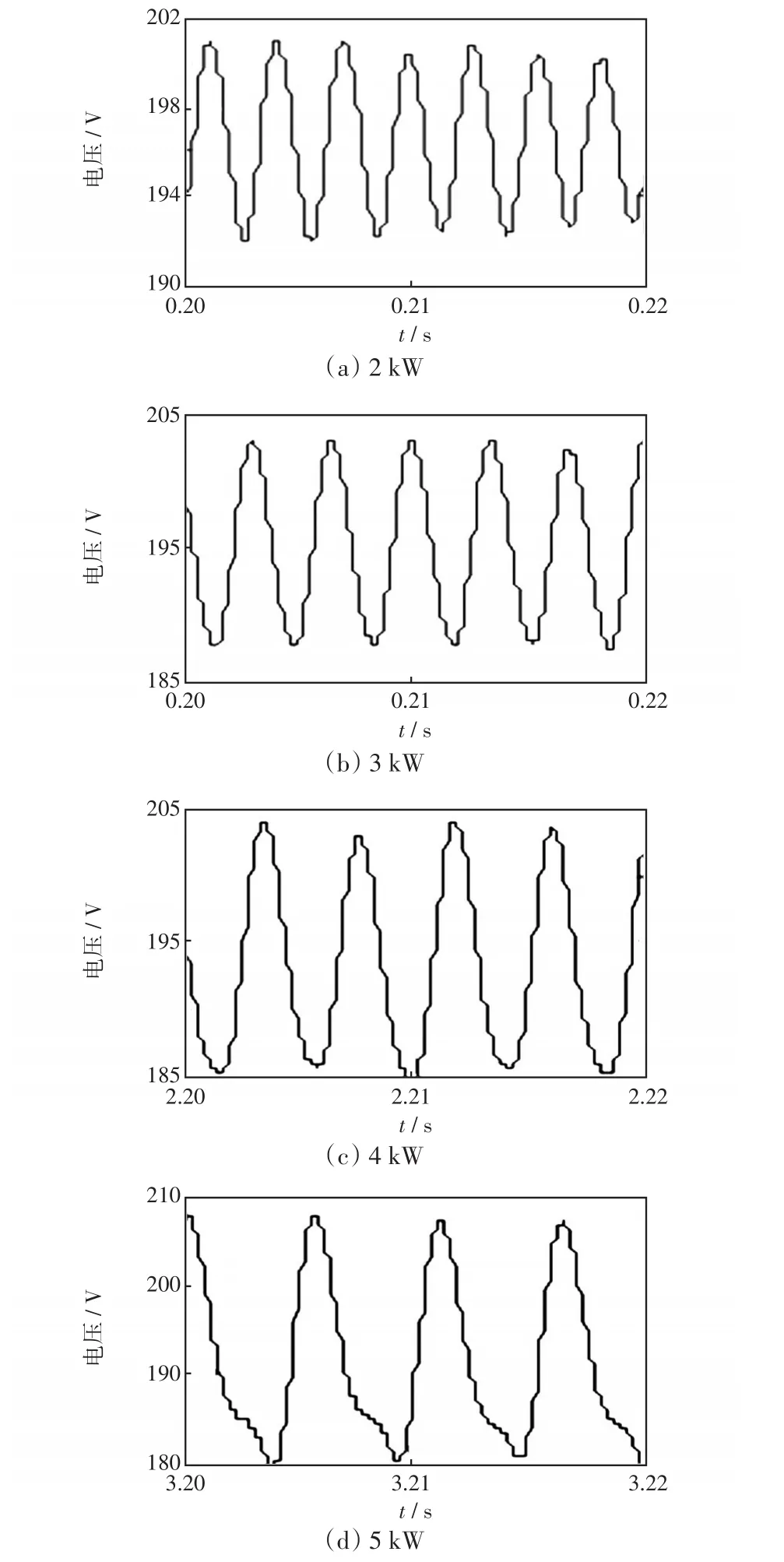
图14 母线电压振荡局部图Fig.14 Partial diagram of bus voltage oscillation

图中（a）、（b）、（c）、（d）分别是恒功率负载为2 kW、3 kW、4 kW、5 kW的局部波形图。

振荡幅度分别为：（z）10 V、（b）16 V、（c）20 V、（d）30 V；振荡频率分别为：（a）345 Hz、（b）287 Hz、（c）237 Hz、（d）181 Hz。

从上述分析可知，随着恒功率负载的增加，母线电压振荡的幅度逐渐增大，但振荡频率却逐渐减小。其中起振频率为345 Hz，与前述振荡机理分析部分相吻合，即初始振荡频率由LC滤波器参数决定。

为了验证所提控制算法在不同恒功率负载功率等级下的有效性，得到了施加虚拟负电感控制策略后的母线电压波形，如图15所示。施加控制策略后，母线电压振荡消失，验证了所提出的虚拟负电感稳定策略的有效性。

图15 施加控制算法后的母线电压（变恒功率负载）Fig.15 Bus voltage after the application of control algorithm（variable constant power load）

4.2 下垂系数变化

第二种情形，验证所提控制算法在抑制下垂系数变化引起母线电压振荡时的有效性。此时系统恒功率负载为1.5 kW。

如图16所示，1.5 s之前，下垂系数Rdroop=0.3，母线电压保持稳定。在1.5 s，下垂系数增加为Rdroop=0.5，母线电压发生等幅振荡，振荡幅度为7 V（190～197 V），振荡频率为325 Hz。2.7 s时，下垂系数为Rdroop=0.7，直流母线电压失稳且等幅振荡，振荡幅度为8 V（188～196 V），振荡频率同样为325 Hz。由此可知，随着下垂系数的增加，母线电压失稳振荡；其振荡幅度逐渐增大，振荡频率保持不变。

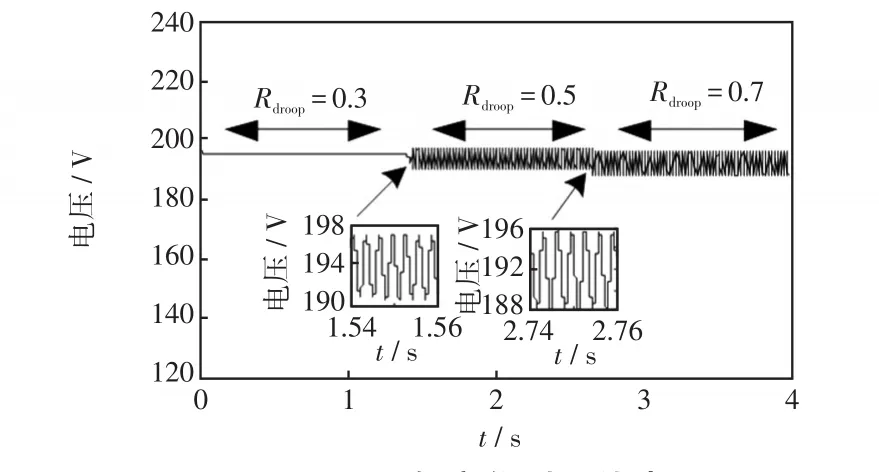
图16 下垂系数变化时母线电压Fig.16 Bus voltage with variation in droop coefficient

如图17所示，施加虚拟负电感稳定策略后，母线电压恢复稳定，振荡消失，验证了所提控制策略在抑制由下垂系数引起母线电压振荡时的有效性。

图17 施加控制算法后的母线电压（下垂系数变化）Fig.17 Bus voltage after the application of control algorithm（variable droop cofficient）

4.3 滤波电容变化

第三种情形，验证所提控制算法在LC滤波器电容变化引起母线电压振荡时的有效性。此时系统恒功率负载为1.5 kW。

如图18所示，在0～1.5 s，滤波电容Co为500 μF，母线发生等幅振荡。在1.5 s时，滤波电容Co切换为1 000 μF，母线电压振荡，但振荡幅度明显减小。在3 s时，滤波电容Co切换为2 200 μF，振荡消失母线电压恢复稳定。这与前述奈奎斯特稳定性分析部分结果相同，即滤波电容的增加有利于母线电压的稳定。

图18 滤波电容变化时母线电压Fig.18 Bus voltage when filter capacitance changes

如图19所示，施加虚拟负电感稳定策略后，母线电压振荡消失，验证了所提控制策略在抑制由滤波电容减小引起母线电压振荡时的有效性。

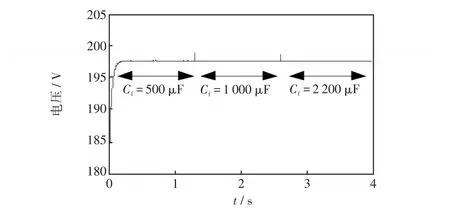
图19 施加控制算法后的母线电压(变滤波电容)Fig.19 Bus voltage after the application of control algorithm（variable filter capacitance）

5 结语

本文以船舶直流微网源-荷级联系统为研究对象，针对LC滤波器与恒功率负载引起的母线电压振荡问题，提出了一种基于虚拟负电感的有源阻尼控制策略。该策略通过对传统的下垂控制方法的改进，在源侧变换器构造了一个虚拟负电感。构造的虚负电感抵消了LC滤波器的电感，提高了系统的阻尼，抑制了直流母线电压振荡。为了摆脱虚拟负电感稳定策略对输出电流传感器较强的依赖性，进一步利用非线性扰动观测器来估计输出电流，保证了系统在输出电流传感器发生故障时，也可正常运行。从系统小信号模型推导出最小回路增益，利用奈奎斯特判据分析了CPL功率变化、下垂系数变化和LC输入滤波器电容变化对系统稳定性的影响，验证了所提控制算法对系统参数变化具有较强的鲁棒性。最后通过仿真实验，验证了所提控制策略的有效性。