基于输入电流和输出电压的Vienna整流器单管开路故障诊断方法

姚 芳，陆 乐，王刘浏，李超峰，唐圣学

（1. 河北工业大学 电气工程学院 省部共建电工装备可靠性与智能化国家重点实验室，天津300130；2. 河北工业大学 电气工程学院 河北省电磁场与电器可靠性重点实验室，天津300130；3. 中国长江电力股份有限公司，湖北 宜昌443002）

0 引言

三相三电平Vienna 整流器与传统整流器最大的区别在于，它是一种中点箝位结构整流器，具有更加灵活的控制策略［1-3］。与其他三电平整流器相比，三相三电平Vienna 整流器具有开关器件少、开关应力小、谐波畸变率低和可靠性高等优点，被广泛应用于整流效果要求较高的领域［4-5］。

目前专门针对Vienna 整流器的故障诊断方法并不是特别多，可以参考其他功率变换器的故障诊断经验。工业应用数据统计显示，由于主要元器件故障而导致的功率变换器故障中，功率电容和功率开关管故障占比最高，故障率分别达到30%和26%［6］。其中功率开关管的故障主要分为短路故障和开路故障［7］。短路故障的研究相对成熟，短路保护主要有过流保护和欠压保护，都是基于短路发生时电流瞬时增大的故障特性。而开路故障发生时，电流的畸变程度相对较小，尤其是当负载较轻时，流过功率开关管的电流比较小，开路故障不易被短路保护检测到，长时间带故障运行会导致电气参数的恶化，容易造成二次故障。因此，为了提高功率变换器的可靠性，相关的开路故障诊断技术研究近几年受到广泛关注。目前的开路故障诊断方法大致分为基于电流特性和基于电压特性两大类。

当开路故障发生时，电流会产生最直接明显的变化，通过分析电流瞬时值和变化率，可以实现故障诊断［8］。针对牵引整流器，文献［9］提出了利用网侧电流的谱峭度进行故障模式识别、利用故障前后电流均值进行故障定位的开路故障诊断方法，但该方法会受到干扰的影响，需配合其他滤波算法。开路故障发生后，谐波特性也会发生改变，文献［10］提出通过分析相电流直流分量进行故障诊断。为了提高诊断的准确性，不少学者将相电流进行矢量变换，利用平均电流矢量［11］或电流矢量角［12］进行故障诊断，但噪声干扰或者负载波动等情况会影响这些方法的诊断效果。

一些基于电压特性的方法，利用特定的硬件来检测特定位置的实际电压，然后分析测量值与理论值的残差，实现故障诊断［13-15］。但是这些方法往往需要增加额外的传感器来提取特征变量，会增加系统的不稳定性，成本较高，通用性较差。针对这些缺点，一些文献提出了不需要增加额外硬件的诊断方法。文献［16］针对Vienna 整流器，将人工神经网络引入开路故障诊断中，利用电流直流分量和电压交流纹波作为训练样本，能够同时诊断功率开关管和二极管的开路故障。文献［17］利用系统已知的直流侧电压，结合模型参考自适应系统技术，设计了一种逆变器开路故障诊断方法。文献［18］采用电压观测器来估算实际的功率变换器电压，具有良好的鲁棒性。文献［19］引入滑模观测器（SMO），用于检测模块化多电平变换器的故障。这些方法不需要添加额外的测量元件，方便集成到已存在的控制系统中，但是往往需要多个周期的运行数据作为支撑，数据处理量大，计算复杂。

通过分析上述文献可知，基于电流特性的诊断方法受输入电流波动和负载波动的影响，基于电压特性的诊断方法往往需要额外设备或复杂计算。考虑到功率变换器大部分的多元件故障都是因为单元件故障未及时处理、长时间带故障运行才导致的二次故障，真正的多元件同时发生故障的概率很小。

本文针对Vienna 整流器单管开路故障，提出了一种准确、可靠、简单的诊断方法。该方法利用故障时输入电流的零值稳区以及输出电容电压差的谐波特性，能够实现单管开路故障的辨识和定位。所提出的故障诊断方法能够配合其他容错策略，保障开路故障时电路仍能正常连续工作，并且不需要添加额外硬件设备，方便集成到已有的控制系统中以实现在线诊断，具有成本低、准确性好、可靠性高等优点，在实际工程应用中能够提高Vienna 整流器的运行可靠性，并且具有较高的可行性。最后通过仿真和实验验证了所提故障诊断方法的准确性和可靠性。

1 单管开路故障特性分析

1.1 Vienna整流器

图1 为三相三电平Vienna 整流器的拓扑结构。图中，ek（k=a，b，c）、ik分别为输入电压和输入电流；Rk为等效串联电阻；Lk为滤波电感；Dkj（j=1，2）为续流二极管；Skj为功率开关管；DSkj为反并联二极管（实际应用中用功率开关管的寄生二极管代替）；C1和C2为直流侧滤波电容；UC1和UC2为滤波电容电压；RL为负载电阻；Uo、io分别为直流侧输出电压、电流；ip和in分别为直流母线正向和负向电流。

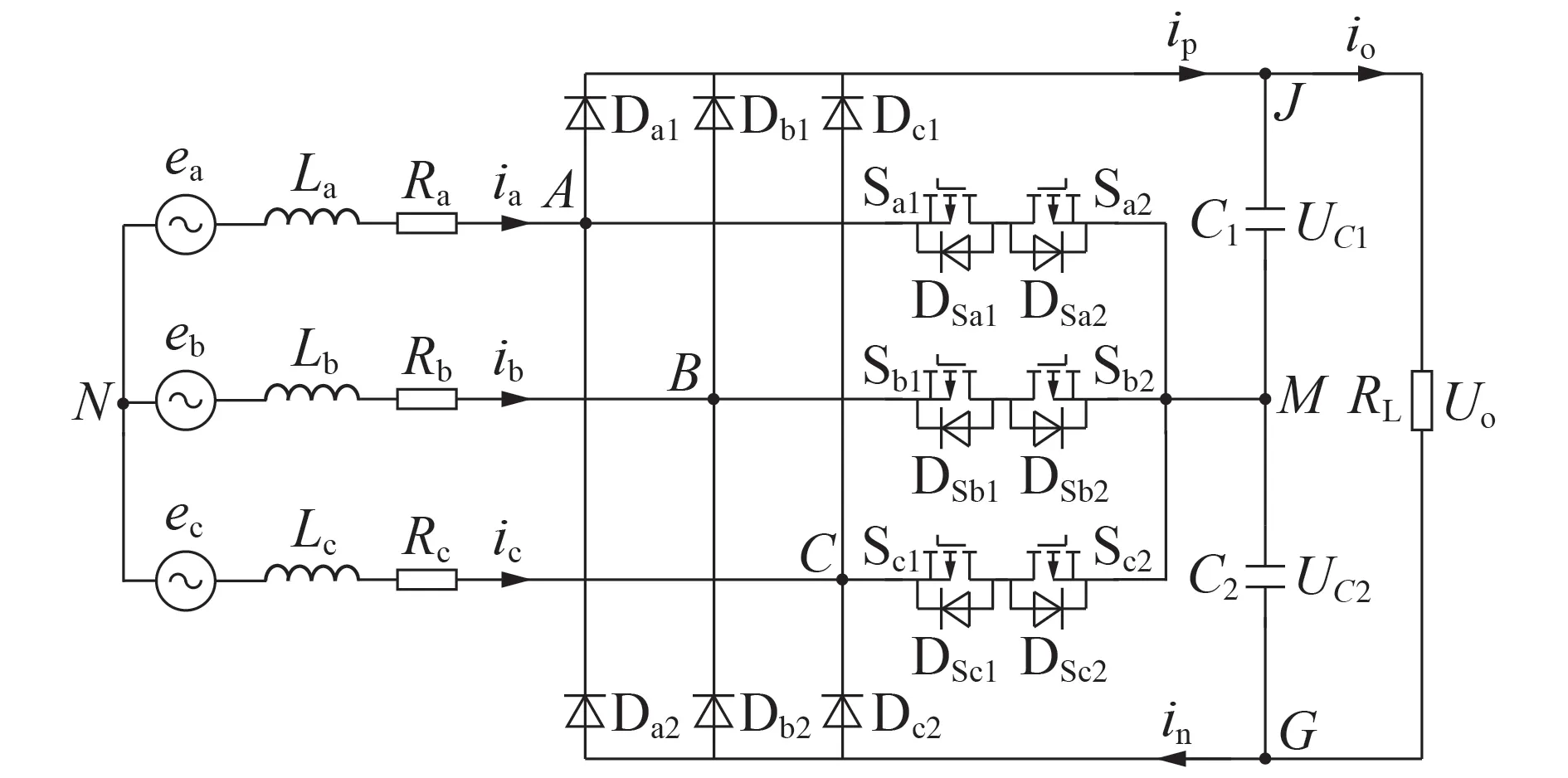
图1 三相三电平Vienna整流器拓扑Fig.1 Topology of three-phase three-level Vienna rectifier

Vienna 整流器的每一相桥臂均由一对方向相反的功率开关管组成，同一桥臂的2 个开关管驱动信号相同，保证同一时刻每一相最多只有1 个开关管导通。每一相的开关状态可以用开关函数Sk表示为：

1.2 输入电流故障特性分析

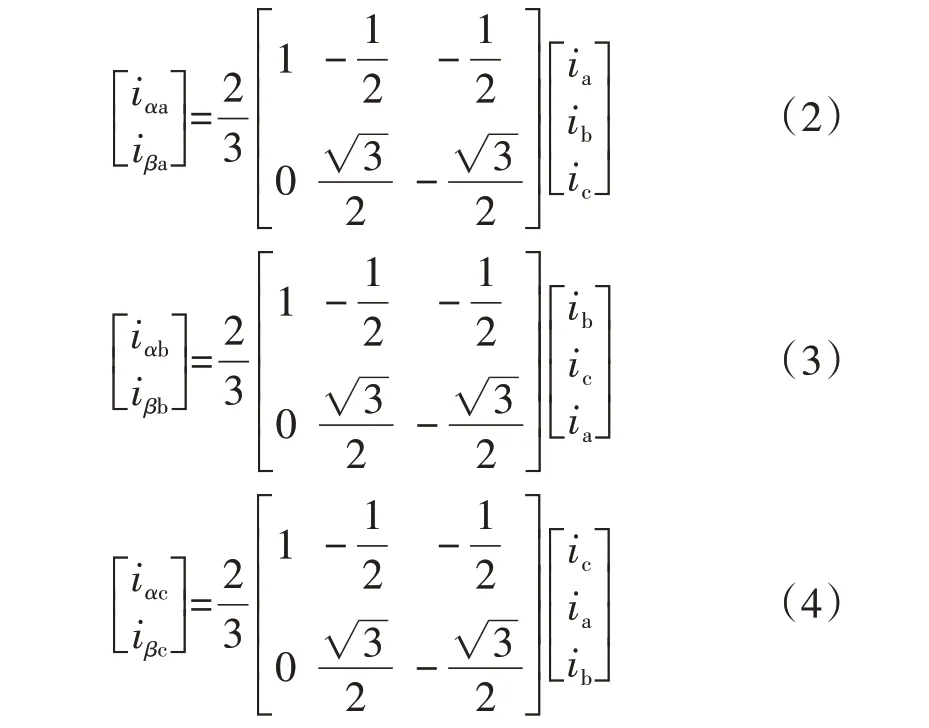
功率开关管开路故障是Vienna 整流器最常见的开路故障类型，本文提出的诊断方法将三相输入电流经过Clark 变换后，得到每相的变换电流iαk和iβk作为故障特征量，三相的Clark变换公式为：

以a 相为例，图2（a）、（b）分别为Sa1、Sa2在0.10 s发生开路故障时输入电流的瞬时值波形和经过Clark变换后的电流波形。

图2 Sa1和Sa2发生开路故障时的输入电流波形Fig.2 Waveforms of input currents under open-circuit fault of Sa1 and Sa2

1.2.1iαk的零值稳区

由图2 可以发现：当Sa1发生开路故障时，iαa正半周出现零值稳区；当Sa2发生开路故障时，iαa负半周出现零值稳区。非故障相电流波形会发生一定程度的畸变，且幅值有所增大。

以开关管Sa1发生开路故障为例，三相输入电流的关系为：

分析式（2）、（5）可知，iαa出现零值稳区的原因是ia同时也出现零值稳区，结合Vienna 整流器的拓扑结构，出现上述输入电流故障特性的原因如下。

1）当电角度处于（0°，180°］时，Sa2被反并联二极管DSa2短路，若Sa1开路，则只有Sa=0 一种情况。忽略二极管导通压降，若续流二极管Da1两端电压UAN≤UJN，则Da1不导通，ia失去通路，形成零值稳区。随着输入电压的变化，当UAN＞UJN时，Da1导通，ia通过Da1流入直流侧形成通路，出现电流尖峰。

2）当电角度处于（180°，360°］时，Sa1被反并联二极管DSa1短路，此时无论Sa1是否故障，都不会影响开关函数Sa的取值，所以ia基本正常。

3）由于三相输入电流满足基尔霍夫电流定律，零值稳区的出现会使非故障相电流发生畸变、幅值增大。

Sa2发生开路故障的原理与Sa1类似，只是分析时电流方向相反，b相和c相的故障特性与a相相同。

1.2.2iβk的正负特性

由图2 可知，无故障时iβa比iαa滞后90°且波形几乎相同，为了便于比较，将iβa延迟0.75T（T为工频周期）。当Sa1、Sa2发生开路故障时，iαa和延迟后的iβa波形分别见附录A 图A1（a）、（b）。可以看出，正常工作时，iαa和延迟0.75T后的iβa波形几乎一致；当上桥臂开关管Sa1开路时，iαa正半周出现零值稳区，此时iβa为正值；当下桥臂开关管Sa2开路时，iαa负半周出现零值稳区，此时iβa为负值。

1.3 输出电压故障特性分析

由文献［4］可知正常运行时，三相桥臂电压开关函数的基波分量dk为：

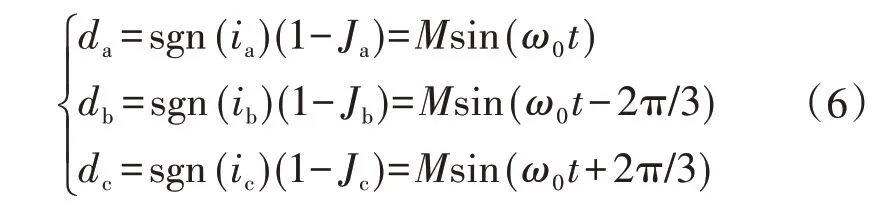
式中：M为调制比；Jk为开关函数基波分量；ω0为角速度；sgn(ik)为符号函数，ik≥0时为1，ik＜0时为-1。

直流侧电压与电流的关系为：

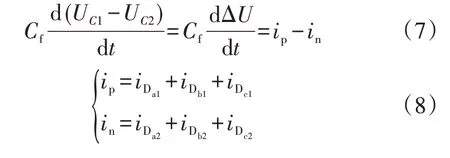
式中：Cf为输出电容；ΔU为输出电容电压差，后文简称为输出电压差；iDk1和iDk2分别为各个桥臂正向和负向续流二极管的电流。

结合式（6）—（9）可得：

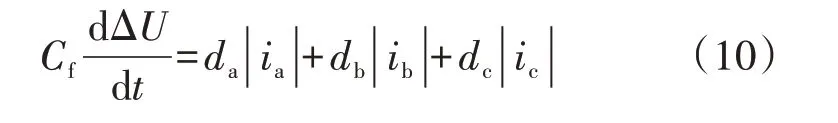
三相输入电流为：

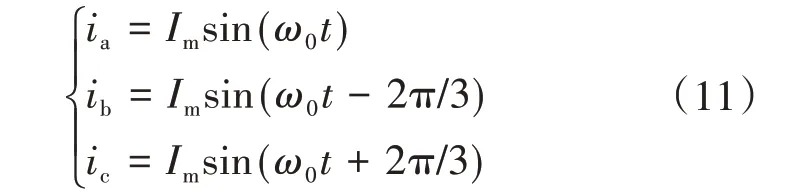
式中：Im为输入电流幅值。

由式（6）、（10）、（11）可得输出电压差为：

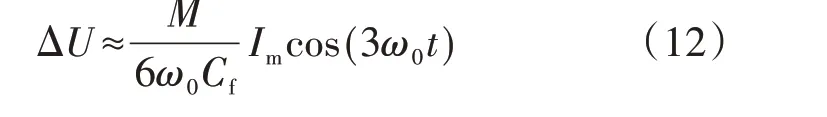
式（12）表明，输出电压差主要为3次谐波分量。

通过分析输入电流的故障特性可知，故障相电流存在零值稳区和电流尖峰2 种故障状态，以Sa1发生开路故障为例进行分析。电流处于零值稳区时开关管和续流二极管均不导通，电流失去通路；电流处于电流尖峰时续流二极管导通，电流经续流二极管流入直流侧。

1）电流处于零值稳区时。

此时式（9）中Da1的电流为：

由式（6）—（9）、（11）、（13）可得：

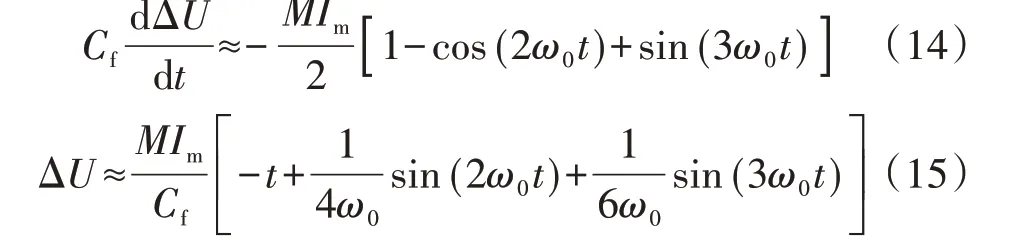
式（15）表明，当单管开路故障电流处于零值稳区时，输出电压差的直流分量和2 次谐波分量会明显升高。

2）电流处于电流尖峰时。

此时式（9）中Da1的电流为：

由式（6）—（9）、（11）、（16）可得：

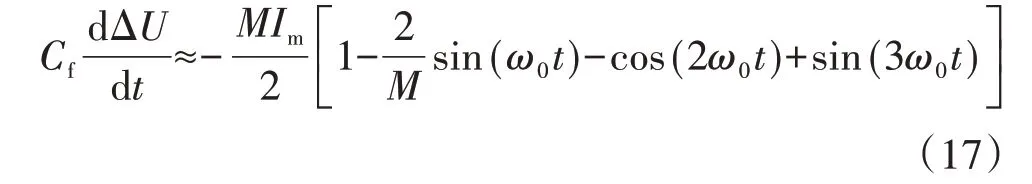
由式（17）可得：

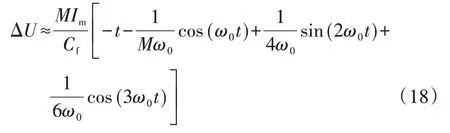
式（18）表明，当单管开路故障电流处于电流尖峰时，输出电压差的直流分量、基波分量和2 次谐波分量会明显升高。

2 单管开路故障诊断方法设计

通过分析故障特性可知，单管开路故障会使输入电流出现零值稳区、输出电压差谐波发生变化。所提出的故障诊断方法利用输入电流进行故障辨识和定位，利用输出电压差进行漏诊检测。

单管开路故障诊断流程如图3所示。图中，ith为零值稳区检测的电流阈值；tth为故障辨识的时间阈值；Ath为直流分量检测的幅值阈值；A0为输出电压差经过快速傅里叶变换（FFT）分析后直流分量的幅值；Fk为故障相定位标志；Fup和Fdown为每相故障桥臂定位标志；F为漏诊检测的故障标志位。

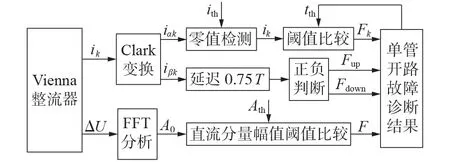
图3 单管开路故障诊断流程Fig.3 Flowchart of single switch open circuit fault diagnosis

所提出的单管开路故障诊断方法主要分为两部分。首先，将三相输入电流经过Clark 变换后，检测iαk的零值稳区时间，进行故障辨识并确定故障相，将iβk延迟0.75T后，根据iβk的正负特性，定位故障桥臂；其次，针对调制比过小时可能会出现漏诊的问题，对输出电压差进行谐波分析，通过检测直流分量的幅值变化进行漏诊检测，当检测结果与故障诊断不一致时，自动调整时间阈值大小。

2.1 基于输入电流的故障辨识和定位

2.1.1 故障辨识

当发生单管开路故障时，Vienna 整流器三相输入电流经过Clark 变换后，iαk会出现明显的零值稳区。因此，可以通过检测是否存在零值稳区进行故障辨识，同时确定故障发生相。

在实际工况下，由于谐波、噪声、负载波动、控制误差等因素的影响，电流处于零值稳区时，并不是完全保持为0，而是围绕0存在微小的波动。设定检测零值稳区的电流阈值ith，若-ith≤ik≤ith则认为此时电流为0，ith的选取会影响检测精度，ith过小可能会导致漏诊断，ith过大可能会导致误诊断，本文结合实际实验结果，设定ith为峰值电流的10%。定义零点标志位εk为：

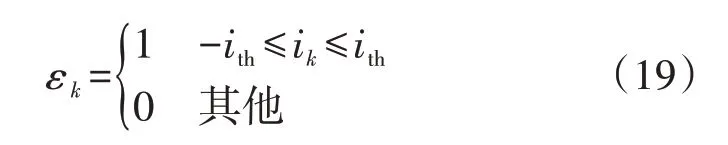
式中：εk=1 表示ik处于零值稳区；εk=0 表示ik不处于零值稳区。

当εk由0 置为1 时，进入零值稳区的检测程序，计数器Wk进入工作状态。在每个采样周期内，若εk保持为1 则Wk累加1，若εk变为0 则计数器不动作。电流处于零值稳区时，由于干扰的原因，电流可能在某一瞬间大于电流阈值，为了提高鲁棒性，设定计时器的工作状态持续时间固定为Tp，当工作状态结束时，计时器进入休眠状态并且清零。电流的零值持续时间tk表示为：

式中：Ts为电流采样周期。

然后，将输入电流的零值持续时间与时间阈值tth进行比较，若tk＞tth则认为电流处于零值稳区，若tk≤tth则认为电流处于自然换零点。与ith同理，tth的取值会影响诊断的准确率和速度，tth过小可能会在自然换零点出现误诊断，tth过大会增加诊断时间，本文结合实际实验结果，设定tth=0.2T。定义故障相标志位Fk为：

式中：Fk=1 表示k相发生单管开路故障；Fk=0 表示k相正常。

2.1.2 故障定位

在进行故障辨识的同时确定了故障相，每一相有2 个功率开关管，分别位于上、下桥臂，只要再确定故障功率开关管所在的桥臂，就能实现故障定位。通过分析故障特性可以发现，三相输入电流经过Clark 变换后，当iαk进入零值稳区时，对延迟0.75T后的iβk进行正负判断，就可以定位故障功率开关管所在桥臂。

因为存在各种干扰和波动，零值稳区过程中，iβk并不一定全为正值或全为负值，所以利用累加的方式考虑整个过程的正负情况。以a 相为例，由式（2）、（5）可知，ia和iαa的零值稳区是同时产生的，设置2个触发计时器Wβk1和Wβk2，它们和计时器Wk同时进入工作状态且持续时间也为Tp。将iβk延迟0.75T，计数器进入工作状态时，若iβk＞0则Wβk1加1，若iβk＜0则Wβk2加1，工作状态结束后清零。定义各相故障桥臂标志位Fup和Fdown分别为：

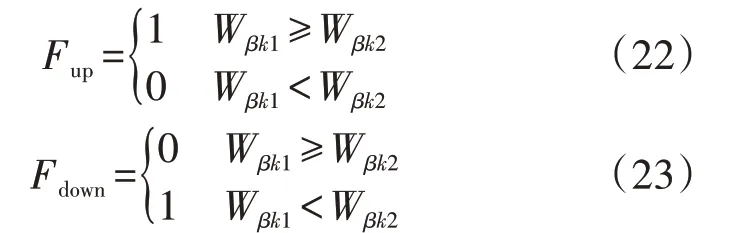
式中：Fup=1 表示故障管在上桥臂；Fdown=1 表示故障管在下桥臂。

故障辨识和故障定位同时进行，故障位置与故障标志位的对应关系见附录A表A1。

2.2 基于输出电压的漏诊检测

较大的时间阈值tth可以避免电流自然换零时出现误诊断，但当调制比过小时，零值稳区时间缩短，可能导致零值持续时间小于tth，造成漏诊断，影响诊断结果的可靠性，因此加入漏诊检测来调整tth大小。利用输出电压差的谐波特性进行漏诊检测，由于电容电压的滞后性，漏诊检测的时间要长于基于输入电流的故障辨识时间，但受波动影响小，诊断结果更加可靠。

收集前一周期的输出电压差数据进行FFT 分析，由于硬件条件的原因以及频率波动的影响，实验中很难取得与工频成倍数关系的频率分辨率，因此选取容易获得且相对稳定的直流分量幅值A0作为故障特征量。若A0≥Ath，则判定发生了单管开路故障。定义漏诊检测标志位F为：

式中：F=1表示发生漏诊断；F=0表示未发生漏诊断。

漏诊断时基于输入电流的故障诊断无故障定位标志，基于输出电压的漏诊检测出现故障标志。此时，自动减小时间阈值，直至出现故障定位标志，消除漏诊断。时间阈值变化量与调制比呈线性关系，如式（25）所示。

3 仿真和实验验证

为了验证所提出的单管开路故障诊断方法的有效性和快速性，搭建了Vienna 整流器的仿真模型和实验平台，分别进行了仿真和实验验证，仿真和实验参数一致，见附录A表A2。

3.1 故障诊断方法的有效性验证

3.1.1 仿真验证

以Sa1为例，利用Simulink 仿真验证所提诊断方法的有效性，在0.1 s 时Sa1发生开路故障，故障相定位和故障桥臂定位的仿真结果分别见附录A 图A2、A3。由图可知，故障发生后，ia进入零值稳区，计数器Wa迅速增大，Wb和Wc无明显变化；在0.108 s 时ta＞tth，故障相标志位Fa置1，Wβa1＞Wβa2，故障桥臂标志位Fup置1。

诊断时间与调制比、故障时电流的相位（故障角度）有关，在不同故障角度（0°、4.5°、9°、…、351°、355.5°、360°）和不同调制比（3.3、3.7、4、4.3、4.7、5）下，对Sa1发生开路故障的诊断时间进行仿真，以验证所提故障诊断方法的快速性，诊断时间的仿真结果如附录A 图A4所示。由图可知，Sa1发生开路故障的辨识时间最短约为2 ms、最长约为14 ms。

Sa1发生开路故障时输出电压差的谐波分量如附录A 图A5 所示。由图可知，正常运行时，输出电压差主要是3 次谐波，Sa1发生开路故障后，直流分量、基波分量和2 次谐波明显增加，仿真结果与理论分析基本相符。

3.1.2 实验验证

为了验证所提诊断方法在实际应用中的诊断效果，设计了Vienna 整流器电路，DSP 控制芯片为TMS320F28335，将诊断方法植入控制系统中，实验平台连接图如附录A 图A6 所示，实物图见附录A图A7。

以Sa1发生开路故障为例进行实验，以验证诊断方法的有效性，此时基于输入电流的诊断结果如图4 所示。由图可知，当Sa1发生开路故障时，输入电流进入零值稳区，经过约8 ms 后，Fa和Fup置1，Fb、Fc和Fdown无变化。

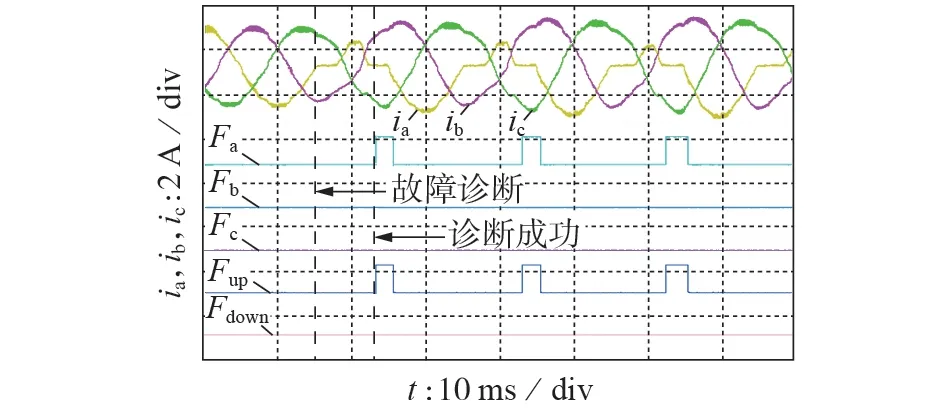
图4 Sa1发生开路故障诊断时的实验结果Fig.4 Experimental result of open circuit fault diagnosis of Sa1

在不同故障角度（0°、4.5°、9°、…、351°、355.5°、360°）和不同调制比（3.3、3.7、4、4.3、4.7、5）下，对Sa1发生开路故障进行实验，以验证所提诊断方法的快速性，诊断时间的实验结果如图5 所示。由图可知，Sa1发生开路故障的辨识时间最短为2 ms、最长为14 ms，实验结果与仿真结果相符。

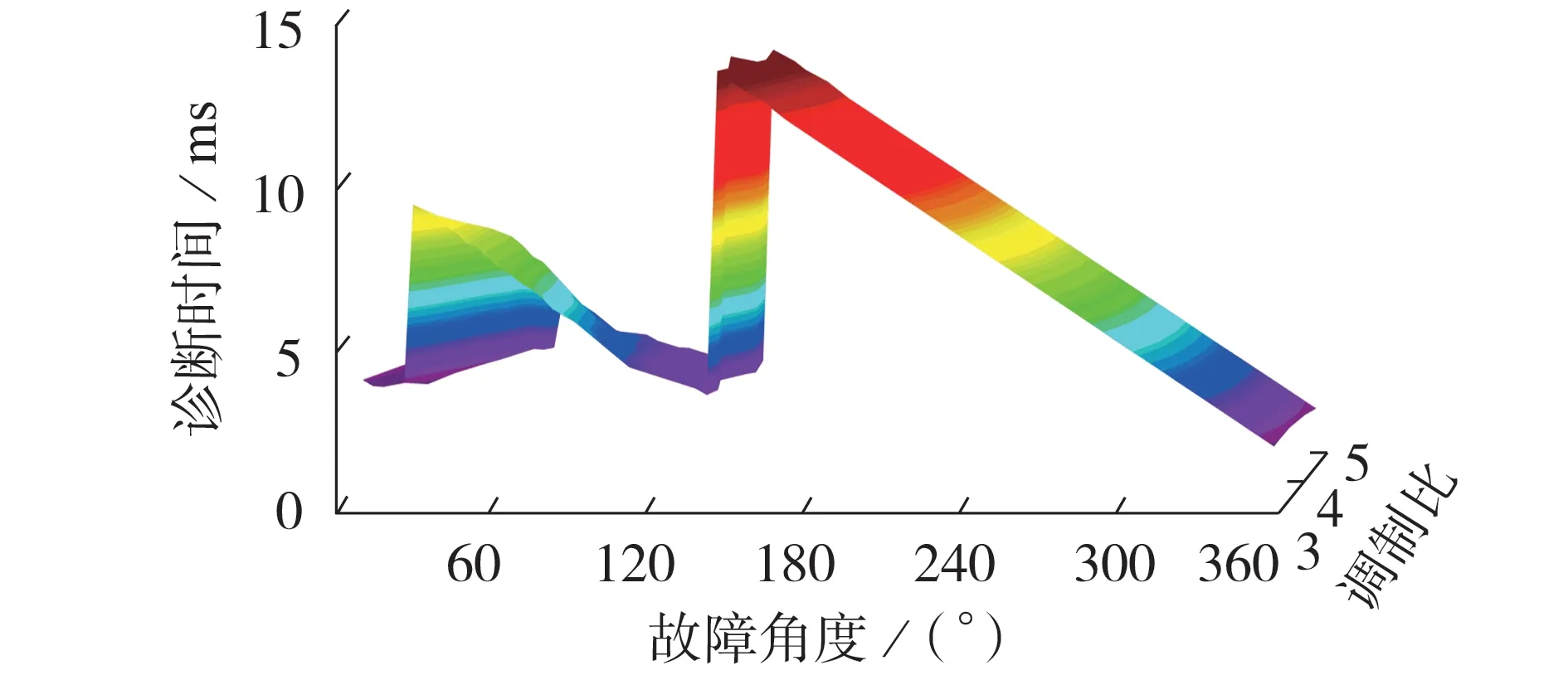
图5 故障诊断时间实验结果Fig.5 Experimental results of fault diagnosis time

其他5 个开关管开路故障的仿真和实验结果与Sa1一致，文中不再赘述。这表明所提故障诊断方法可准确快速地实现单管开路故障的辨识和定位。

当故障角度接近150° 时，诊断时间明显突增，这是因为此时故障发生时刻位于零值稳区末端，计数器计数得到的零值持续时间无法达到诊断阈值，等到下一个零值稳区才能诊断出故障。

漏诊检测的实验结果如图6 所示，实验时采用较小的调制比和较大的时间阈值，模拟故障诊断出现漏诊时的情况。由图可见，单管开路故障发生后，故障诊断由于时间阈值相对较大而没有正确动作。故障发生后约38 ms，漏诊检测正确动作，自动减小时间阈值，约8 ms 后故障诊断正确动作，避免了漏诊断。

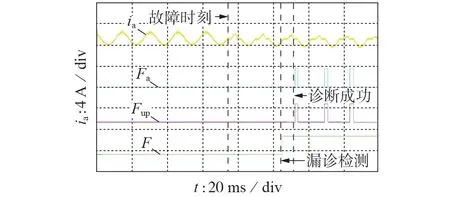
图6 漏诊检测实验结果Fig.6 Experimental results of missing diagnosis test

3.2 故障诊断方法的鲁棒性验证

本节从网侧电能质量干扰和负载突变2 种情况出发，验证所提故障诊断方法的鲁棒性，其中网侧电能质量干扰分为三相电压不平衡和电压谐波干扰。由于实验室无模拟网侧电能质量干扰的设备，这一情况下的鲁棒性由仿真进行验证，负载突变时的鲁棒性由实验进行验证。

3.2.1 网侧电能质量干扰下的鲁棒性

网侧三相电压不平衡条件下，所提故障诊断方法鲁棒性的仿真验证结果见附录A 图A8。电压不平衡条件为ua=1.2ub=1.2uc，uc=30 V，幅值差为20%，三相电压不平衡度远超过IEEE Std 112—1991、IEEE Std 1159—1995、IEC61000、GB／T 14549—93规定的电能质量标准。在0.15 s 之前，由于三相电压不平衡，输出电压存在脉动，a相电流幅值较大，但保持动态稳定。在0.15 s 时，开关管Sa1发生开路故障，故障标志位正确置位，所提故障诊断方法迅速准确地完成了开路故障的辨识和定位。由图A8可知，三相电压不平衡时，所提故障诊断方法不会误诊断，且单管开路故障发生时能正确动作。

输入电压存在较大低次谐波干扰时，所提故障诊断方法鲁棒性的仿真验证结果见附录A 图A9。各相含有10%的5 次谐波和5%的7 次谐波，谐波含量远超过IEEE Std 112—1991、IEEE Std 1159—1995、IEC61000、GB／T 14549—93规定的电能质量标准。在0.15 s 之前，由于输入电压低次谐波含量较大，输入电流波形存在明显畸变，但保持动态稳定。在0.15 s时，开关管Sa1发生开路故障，故障标志位正确置位，所提故障诊断方法迅速准确地完成了开路故障的辨识和定位。由图A9可知，在输入电压存在较大低次谐波干扰条件下，所提故障诊断方法不会误诊断，且单管开路故障发生时能正确动作。

3.2.2 负载突变时的鲁棒性

Vienna 整流器正常运行时，将负载由100 Ω 突变为50 Ω，所提故障诊断方法的鲁棒性实验验证结果如图7 所示。由图可知，所提故障诊断方法在负载突变时不会误诊断。

图7 负载突变时故障诊断方法鲁棒性的实验验证结果Fig.7 Experimental verification result of robustness of fault diagnosis method under sudden load change

3.3 故障诊断方法比较

本节从诊断时间、鲁棒性、阈值调整、实现成本、计算复杂度等角度出发，将本文提出的故障诊断方法与已有研究中的三相整流器开路故障诊断方法进行比较，结果如表1所示。

表1 不同故障诊断方法之间的比较Table 1 Comparison among different fault diagnosis methods

由表1可以得出如下结论。

1）诊断时间：所提出的故障诊断方法能够在（10%～70%）T内辨识和定位单管开路故障，与其他故障诊断方法相比，诊断速度较快。

2）鲁棒性：所提出的故障诊断方法在网侧电能质量较差和负载突变时，能保持不出现误诊断，单管开路故障发生时，能快速准确动作，具有良好的鲁棒性。

3）阈值调整：所提出的故障诊断方法对阈值调整的依赖较小，只需设置电流阈值、时间阈值和谐波幅值阈值。其中电流阈值和谐波幅值阈值具有较好的通用性，不需要频繁调整，时间阈值能够通过漏诊检测自动调整。

4）实现成本：所提出的故障诊断方法不需要增加额外的硬件设备，成本低。

5）计算复杂度：所提出的故障诊断方法计算简单可靠，所需内存较小，方便集成到控制系统中进一步实现在线诊断。

综合各方面的性能比较，本文提出的故障诊断方法的诊断效果优异，具有诊断速度较快、鲁棒性好、阈值调整少、实现成本低、计算简单可靠等优点。

4 结论

本文利用输入电流的零值稳区和输出电压的谐波特性，设计了一种Vienna 整流器单管开路故障诊断方法，并通过仿真和实验验证了其有效性和快速性，所得结论如下：

1）所提出的诊断方法基于输入电流的零值稳区进行故障诊断，时间阈值初值设置足够大，可避免误诊断，同时基于输出电压差实现漏诊检测，自动调减时间阈值，直至故障标志位成功置位，可避免漏诊断；

2）所提出的诊断方法在不同故障角度、不同调制比和负载突变情况下，均能快速、准确、无漏地进行单管开路诊断，诊断时间在（10%～70%）T之间；

3）所提出的诊断方法简单可靠，无需添加额外硬件，可直接将诊断程序嵌入Vienna 整流器控制芯片，实现Vienna整流器单管开路故障在线诊断。

附录见本刊网络版（http：//www.epae.cn）。