基于EFA-GA-XGBoost组合预测模型的绝缘子表面污秽程度预测方法
2022-03-17赵昕迪
赵昕迪
(重庆科技学院,重庆,401331)
0 引言
近年来,XGBoost算法在电力系统领域得到了广泛的应用,在换流站状态评估、电网攻击检测和异常用电识别等方面均取得较好的效果,但在电力设备外绝缘状态评估领域的应用研究仍有欠缺。考虑到单一的预测模型由于自身的局限性,并不能取得满意的预测结果。而组合预测模型可以整合单一模型的优点,通过模型之间的优势互补,增强预测效果,有效提高预测精度和计算速度。
1 绝缘子污秽程度关联因素
1.1 泄漏电流
泄漏电流随绝缘子表面污秽程度的变化呈现出不同的发展趋势,能综合的反映绝缘子表面的各种参数,是绝缘子最有效的在线监测参数。基于泄漏电流特性对绝缘子表面污秽程度进行预测具有重要的实用价值。为充分通过泄漏电流分析绝缘子污秽程度,提取有效值Ie、最大值Im、标准差σ、偏斜度Sk及峭度Ku共五个参量。
1)泄漏电流有效值反映了绝缘子在相同气候条件下的污秽程度,有效值越大,积污越为严重,表达式如下:
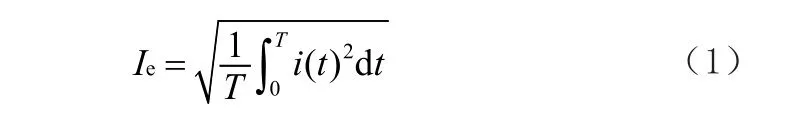
式中,T为采样周期。在线监测系统均以离散信号对泄漏电流进行采样,故将(1)式变型为:
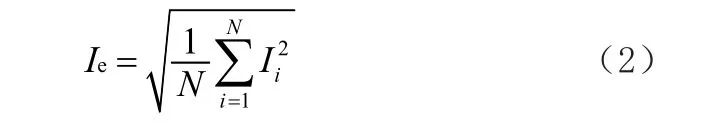
式中,N为采样点数。Ii为i时刻泄漏电流值。
2)泄漏电流最大值反映的是绝缘子污秽表面干带上电流脉冲的大小,其值随干带的厚度和宽度的变化而变化,表达式为:
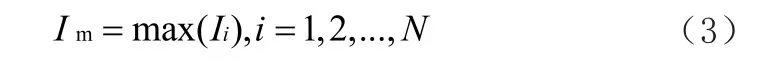
3)泄漏电流标准差反映了脉冲的数量和泄漏电流畸变情况。脉冲数量越多,泄漏电流畸变越严重,则标准差越大,表达式为:


4)泄漏电流偏斜度Sk,反映以泄漏电流幅值期望值为中心的分布不对称度:
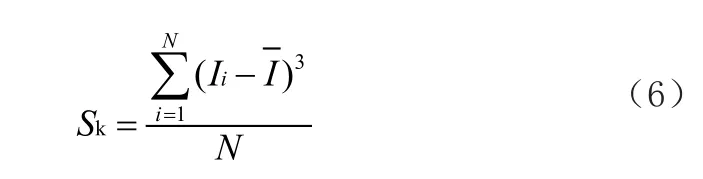
5)泄漏电流峭度Ku,反映泄漏电流的变化陡度:
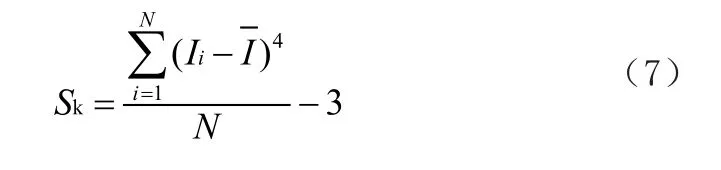
1.2 气象因素
绝缘子长期暴露在自然环境下,会受到各种不良天气的影响,空气相对湿度、温度、降雨、风速等气象因素会直接影响绝缘子表面的积污程度。
空气湿度对污秽形成的影响较为显著。当相对湿度较小时,绝缘子表面的范德华力占据主导地位,此时污秽物不易粘附;而当湿度较大时,水膜对空气中染污颗粒的粘附作用增强,绝缘子表面积污速率较快。
温度对积污的影响较小,温度常常与空气相对湿度共同作用才会产生较大影响。当绝缘子处于温差较大的环境中,其表面污秽更易受潮,形成冷凌现象,易发生污闪事故,即。
降雨对绝缘子表面污秽的影响较为复杂,连绵细雨与强降雨对绝缘子影响相反。连绵细雨会使得绝缘子表面形成的水膜对污秽颗粒有较强的吸附和粘附作用。但在强降雨时,绝缘子表面的可溶性污秽会显著降低,但对难溶性污秽物冲刷较少。故文章对在考虑降雨对污秽的影响时,参考文献[23]的数据观测结果,将降雨天气按照当日24小时降雨量是否超过10mm分为两类。
风速对绝缘子积污作用是双面性的,一方面,当风速达到一定强度时,迎风侧积污速率加快;另一方面,当风速超过一定阈值时,强劲的风会吹离绝缘子表面的污秽,但强风会产生涡流效应,使绝缘子背风侧积污加聚。
2 EFA理论及算法
EFA算法的的核心是在最小化信息丢失的前提下,将多个研究变量整合为几个易于解释的因子变量,降低模型的复杂度。通过灵活的因子轮换,使每个因子都具有明确的现实意义。
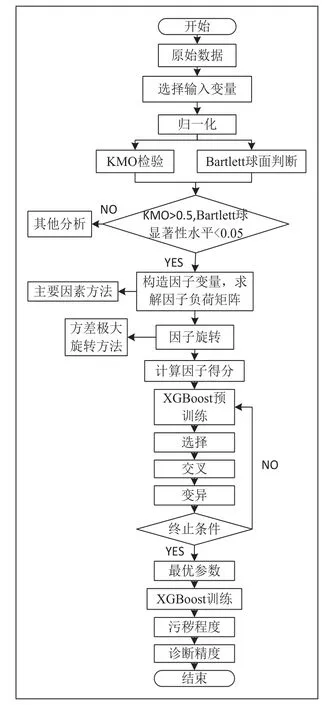
假设n个样本中有p个可观测变量,X=(x1,x2,…,xp)是标准化后的可观测变量。原始变量用m(m 模型的矩阵形式由等式(2)给出: 式中,F为原变量X的因子变量,ε为X的特殊因子,A为因子加载矩阵,aij(i=1,2,…,p; j=1,2,…,m)为因子系数。一般采用0.5原则对原始变量进行筛选,即当因子系数的绝对值大于0.5时,认为因子变量占原始变量的主导地位[32]。 EFA的具体建模步骤如下: 1)判断原始变量是否满足EFA原则。一般采用KMO检验和Bartlett球面进行判断。当采样充分的KMO测量值大于0.5时,且Bartlett球形检验的显著性水平小于0.05时,所研究变量适用于EFA原则。对原始数据进行标准化处理,消除变量间的维数和数量级差异对判断的影响。标准化公式如下: 式中,xi为标准化后的变量,为原始变量的平均值,为原始数据的标准差。 2)构造因子变量。首先选择合适的因子个数,通常采用特征值法来确定因子个数。特征值法用来计算相关系数矩阵的特征值,选取大于1的特征值个数作为因子个数。然后求解因子矩阵。本研究采用主因子法求解问题。具体公式的特征如下: 3)旋转因子以更好地解释因子变量。因子旋转分为正交旋转和斜向旋转。前者使因子变量不相关,而后者允许因子变量相关。本研究采用最大旋转方法对因子变量进行旋转,以保证因子变量之间的不相关性。 4)计算因子得分。计算各因子变量在各样本上的因子得分,将各因子变量的因子得分作为后续预测模型中输入变量的数据。EFA模型通过减少原始变量的维数来简化问题。 本文提出了基于探索性因子分析的GA-XGBoost组合预测模型。所提模型的详细步骤如下。 1)通过EFA方法,对p维的原始变量进行降维,得到m个因子变量和每个因子变量在n个样本上的因子得分。 图1 EFA-GA-XGBoost组合模型算法流程图 3)建立XGBoost 预测模型,进行预训练,并采用GA优化模型参数。 4)判断是否满足的终止条件,若满足,则此时的训练值作为最优参数,否则继续优化模型参数。 5)将测试集数据输入探索性因子分析的GA-XGBoost模型,得到预测结果。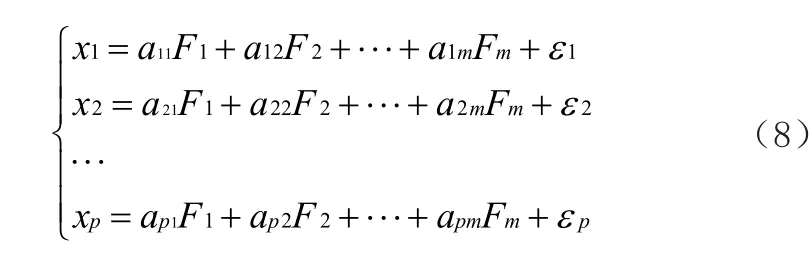

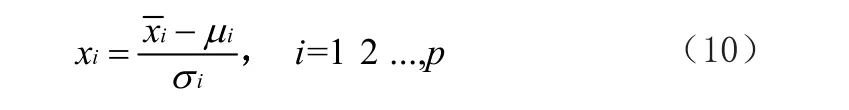

3 EFA-GA-XGBoost组合预测模型