基于灰色模型的变形预测实例应用与对比分析★

杨怀义

（中国建筑材料工业地质勘查中心山西总队，山西 太原 030031）

1 概述

变形监测在建筑物的施工以及运营、滑坡等地质灾害防治、隧道围岩变形等安全监测中广泛应用，是安全监测的实用手段［1］。而在获取变形数据后的变形预测，则是变形数据分析的重要内容。其是根据现有数据对未发生变形进行预测，能够对即将发生的变形有一个初步判断，以对安全措施的制定提供指导，预警和降低可能的损失。目前变形预测方法有多种。而由华中科技大学邓聚龙教授于1982 年提出的灰色GM（1，1） 模型具有小数据样本、贫信息建模的特征［2－4］。而其自提出以来，针对模型方法的改进及应用研究已经取得诸多成果。其中卜璞等［5］针对GM（1，1） 存在的三方面问题，对其进行改进并应用于建筑物变形预测中，取得较好的效果；邱利军等［6］则采用平面坐标变换的方式对建模序列的一次累加值的预测值进行变换，以变换后的折线上的点作为其预测值并还原，从而改进模型并以大坝变形数据以及基坑变形数据进行了验证；王艳艳等［7］则针对均值GM（1，1） 模型对小浪底大坝实测变形数据进行预测分析，从而进行了模型实践应用研究；姚颖康等［8］、王新胜等［9］则分别针对滑坡变形和隧道围岩变形采用改进GM（1，1） 模型和非齐次灰色预测模型进行预测，取得比传统模型好的效果。本文以晋中市某小区18 层楼的沉降实测数据为依据，建立多种GM（1，1） 模型进行拟合预测，并对预测结果进行了对比分析，对工程实际应用及模型选取具有一定意义。

2 几种GM（1，1）模型原理

2．1 原始GM（1，1） 模型和均值GM（1，1） 模型

设序列X（0）=（x（0）（1） ，x（0）（2） ，…，x（0）（n） ） ，其中x（0）（k） ≥0，k=1，2，…，n；X（1）= （x（1）（1） ，x（1）（2） ，…，x（1）（n） ） ，X（1）为X（0）的1 －AGO 序列，计算公式为：

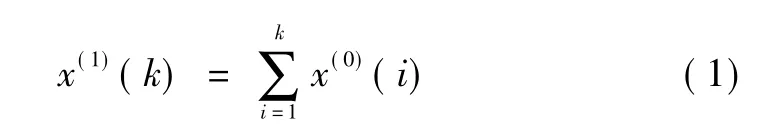
其中，k=1，2，…，n。

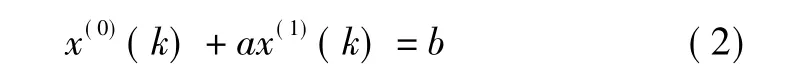
式（2） 为GM（1，1） 模型的原始形式。其中，参数向量^a=［a，b］T，运用最小二乘估计求解：

其中：

基于原始形式的GM（1，1） 模型和式（3） 估计参数，直接以式（2） 的解作为时间响应函数，所得到的模型为原始差分GM（1，1） 模型（ODGM） 。

设X（0）与X（1）如 上 所 示，设Z（1）= （z（1）（2） ，z（1）（3） ，…，z（1）（n） ） ，其中：

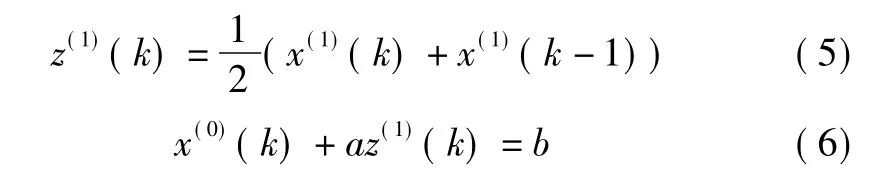
式（6） 为均值GM（1，1） 模型。矩阵B变为：

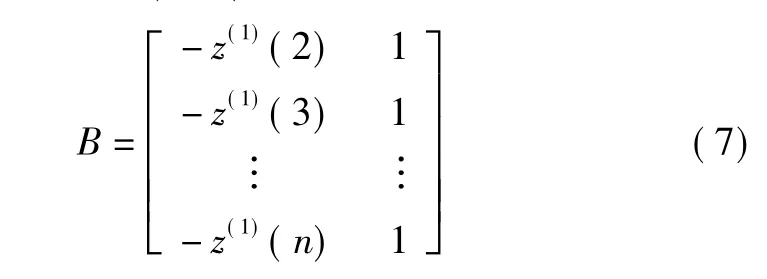
进而采用式（3） 进行式（6） 中参数向量^a=［a，b］T的估算。

式（8） 为均值GM（1，1） 模型的白化微分方程，也称

收稿日期：2021－08－12

★基金项目：张家口科技计划项目（2021028D）；河北省高等学校青年拔尖人才计划（BJ2020010）

作者简介：杨怀义（1988 － ），男，工程师，注册测绘师，从事工程测量方法研究影子方程。

均值GM（1，1） 模型的时间响应函数为：

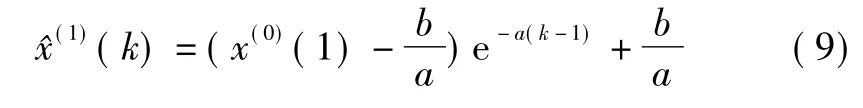
若k≤n为模拟，若k＞n为预测。累减还原式为：

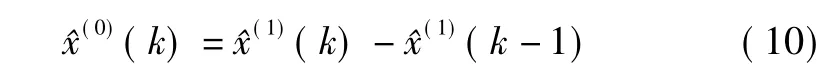
而对应的X（0）的时间响应函数是：

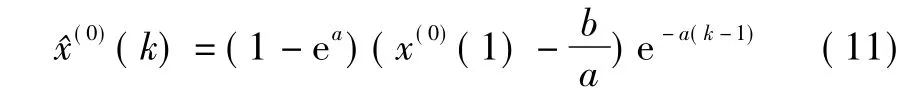
2．2以x（1）（n） 为初始条件的GM（1，1） 模型

设B，Y，^a为均值GM（1，1） 模型所述，^a=［a，b］T=（BTB）－1BTY，则：

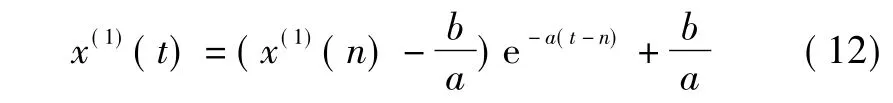
2） 灰色微分方程x（0）（k） +az（1）（k） =b时间响应函数为：

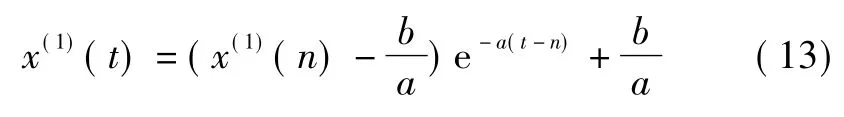
3） 还原值：

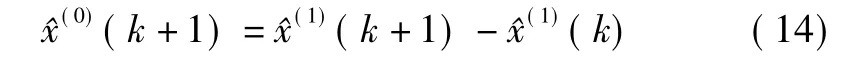
证明过程参见文献［3］。同上：

a．当k≤n时，称^x（0）（k） 为模型模拟值；

b．当k＞n时，称^x（0）（k） 为模型预测值。

2．3 基于Newton-Cotes 公式的GM（1，1） 模型

该方法分析了GM（1，1） 模型的背景值，认为其求法实际上就是数值积分中的梯形法，而梯形法的误差较大，精度也比较低；因此，该方法提出用Newton-Cotes 法代替梯形法重新构建背景值。

在用Newton-Cotes 公式时需要用到如下的数值：

其中，k=1，2，…，n－1。可以利用数值分析中的插值法求出这些值。

依据数值分析相关知识可知，函数f（x） 关于点x0，xk的一阶均差定义为：

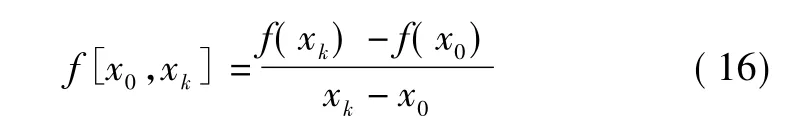
函数f（x） 关于点x0，x1，xk的二阶均差定义为：

函数f（x） 关于点x0，x1，…，xk－2，xk的k－1 阶均差定义为：

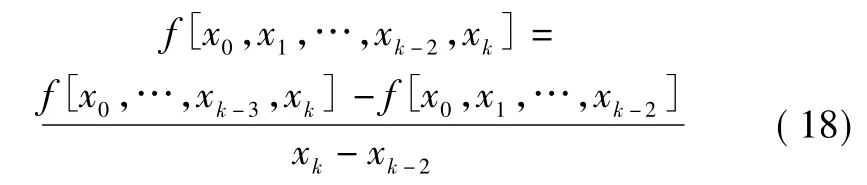
函数f（x） 关于点x0，x1，…，xk的k阶均差定义为：

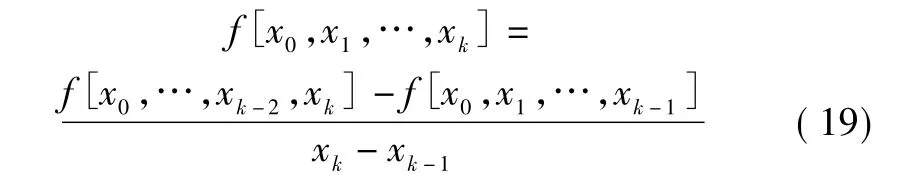
牛顿插值公式：

假设x是［a，b］上一点，可得：

只要把后一式代入到前一式子，就可以得到：

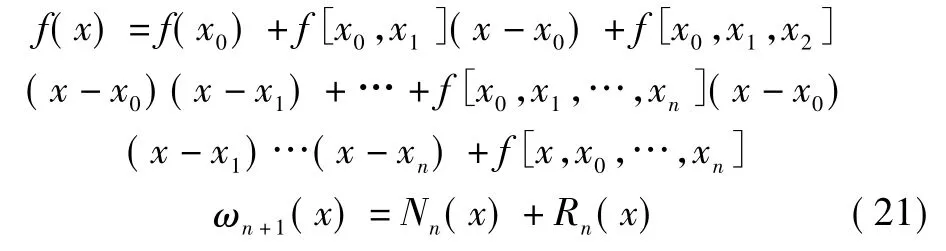
其中：

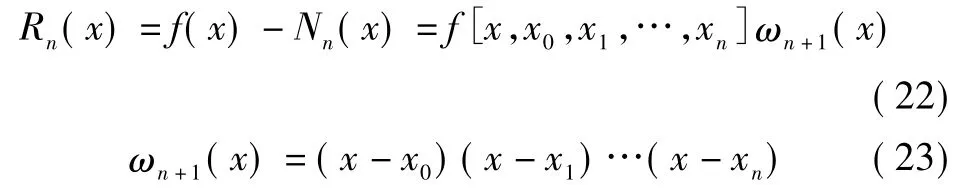
牛顿均差插值多项式为：

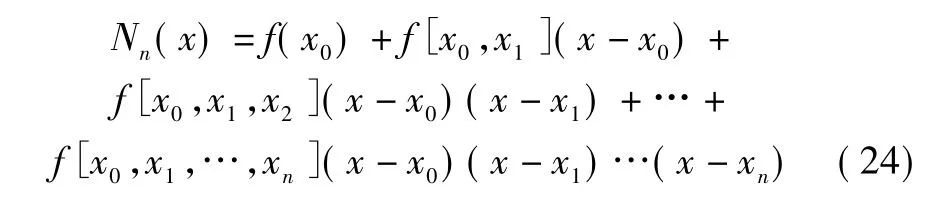
Newton-Cotes 公式：

设将积分区间［a，b］划分为n等分，步长h=，选取等距节点xk=a+kh构造出的差值型积分式：

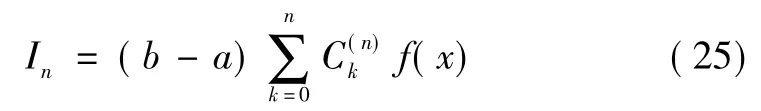
称作Newton-Cotes 公式，式中C（n）称为Cotes 系数。

设x=a+th，则有：

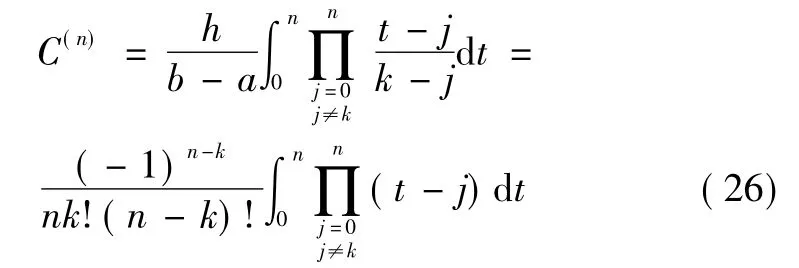
由于是多项式的积分，Cotes 系数的计算不会遇到实质性的困难。

当n=1 时：

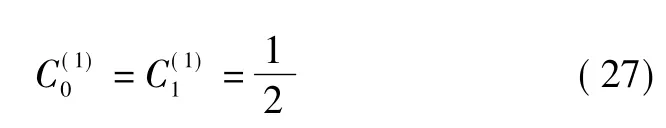
这时的求积公式是我们熟悉的梯形公式。

当n=2 时，这时的Cotes 系数为：

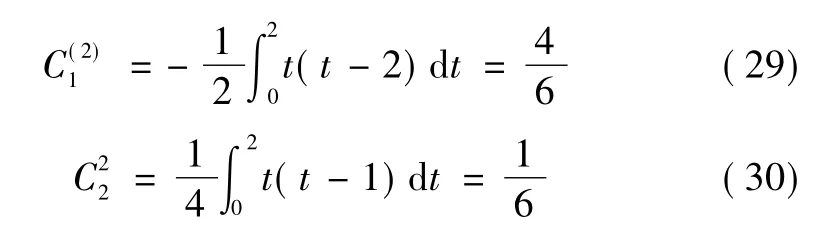
相应的求积公式是Simpson 公式：

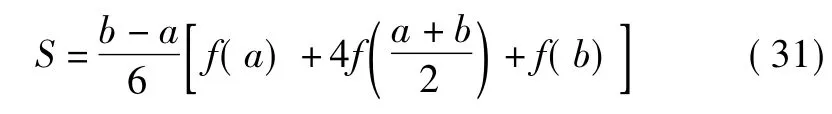
而n=4 的Newton-Cotes 公式则特别称作Cotes 公式，其形式为：

此即改进所用Newton-Cotes 公式。

基于Newton-Cotes 公式背景值改进：

取一次累加序列x（1）= {x（1）（1） ，x（1）（2） ，…，x（1）（n） }，令Y（k） =k，k=1，2，…，n，把［Y（k） ，x（1）（k） ］，k=1，2，…，n作为对应曲线上的等间距点的坐标，用牛顿插

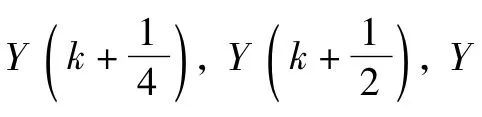
其中，k=1，2，…，n－1。

3 工程实例应用及比较分析

该项目位于晋中市，楼主体为地上18 层，结构形式为钢筋混凝土框架结构。监测目的是掌握该建筑在施工建设和使用过程中的沉降情况，保证建筑施工阶段和使用过程中的安全，并为消除隐患提供科学依据。选用1号沉降观测点实测9 期（第6 期～第14 期） 数据，采用前7 期数据建模，以后2 期数据进行验证。分别建立原始GM（1，1） 模型、均值GM（1，1） 模型、以x（1）（n） 为初始值的GM（1，1） 模型以及基于Newton-Cotes 公式的GM（1，1） 模型，且模型依次记为模型一、模型二、模型三和模型四。其实测数据如表1 所示。

表1 实测变形数据序列

采用C#语言编程对四种模型进行模型实现，并建模预测；预测结果如表2 所示，预测结果的相对误差如表3所示。

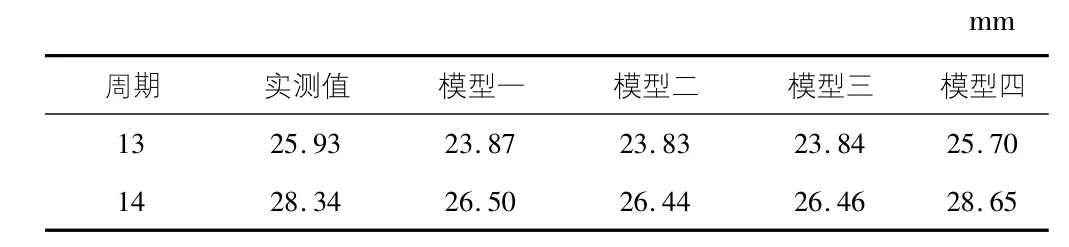
表2 不同模型预测结果

表3 不同模型预测值的相对误差

通过分析表2，表3 可知，模型一、模型二、模型三的预测精度相近，而模型四的预测精度最高。虽然从相对误差表3 分析，模型一、模型二以及模型三的相对误差最大为8．10%，可以接受； 但是考虑到三种模型相对误差最小时（6．49%） ，其残差值为1．84 mm，是针对累计沉降量的绝对误差；而已知数据序列单次沉降量的最大值为4．01 mm。因此，考虑到单次沉降量的量级，前三类预测模型结果是不能接受的。而模型四的残差值分别为0．23 mm 和－0．31 mm，认为达到了较好的预测效果。不同模型与已知数据建模预测结果如图1 所示。从图1 可以看出，模型四曲线在后期预测期中更接近实测数据曲线，但也可以明显看出，四种模型均以单调指数函数形式进行预测，针对波动数据预测存在不足，且适用于短期预测。

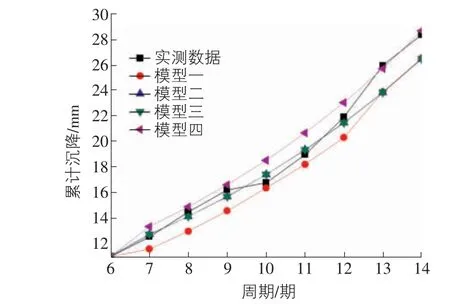
图1 多种模型预测结果比较

4 结语

在工程施工阶段变形发生并持续至运营阶段，而由于外部因素影响也可能引发变形，而变形监测是保障安全的重要手段。本文以变形监测实测沉降数据序列为基础，选取9 期实测数据进行预测实践应用分析，采用7 期建模2 期验证，分别建立的原始GM（1，1） 模型、均值GM（1，1） 模型、以x（1）（n） 为初始值的GM（1，1） 模型以及基于Newton-Cotes 公式的GM（1，1） 模型，在程序实现相关模型的基础上对预测结果进行对比分析，认为基于Newton-Cotes 公式的GM（1，1） 模型预测结果达到了较好的效果，其可以作为相似工程的参考方法。但通过分析可知，本文选用模型均是以指数函数进行预测，应用上存在限制，且一般适用于短期预测。针对长期预测及复杂数据预测问题，需要进一步进行研究。