一种结合有限元程序的桥梁荷载试验分析方法

孟凡侠

（北京安信卓越信息科技有限公司，北京 100088）

1 荷载试验意义

数据统计，我国现有公路桥梁已超过80 万座，其中服役期限超过30 a 的占比约为1/3，这部分桥梁老化现象日益突出；另外20 世纪的大多数桥梁设计荷载和现有规范荷载有一定出入，并且当前超载现象严重，导致很多桥梁存在较大的安全隐患。当前对桥梁的检测方法还是以日常巡检为主，而人工巡检更多的还是基于目测的外观评定为主，通过这种手段很难发现结构的内在损伤情况。

桥梁荷载试验是基于设计文件，同时考虑桥梁服役年限，对设计参数进行适当折减后进行数值模拟，通过计算得到桥梁的理论指标，以及结合现场加载的桥梁的实际反应，通过对实测数据和理论计算值的比对，评定桥梁既有状况的一种方法。相对于传统的人工巡检，不仅仅是对桥梁外观进行判定，静载试验更加容易判断桥梁内在的损伤情况，是目前较为可靠的一种桥梁评定方法［1］。

随着有限元技术的发展，荷载试验作为评定桥梁健康情况也变得越来越可行，可以锁定关键部位的重点响应，再反推加载形式和部位，使得加载问题和理论实际对比变得简单［2－5］。本文以实际背景桥梁为例，进行结合有限元程序的荷载试验方法的说明，并对结合有限元的荷载试验方法注意事项进行探讨。

2 基于背景桥梁的荷载试验分析

2．1 背景桥梁概况

某大桥长928． 85 m（其中主桥长324 m，引桥长604．85 m） 。主桥采用（36 +72 +108 +72 +36） m 钢管混凝土拱连续梁结构形式［6］，引桥采用3 ×32．7 m 预应力混凝土连续箱梁，桥梁建设运营已达15 a 之久，所以有必要对该桥做一个全面的承载能力评定，桥梁布置图如图1 所示。

图1 主桥布置图

2．2 有限元模型建立

对大桥建立有限元分析模型，进行结构分析，主拱、边拱、主梁模拟为梁单元，吊杆模拟为桁架单元。其中梁单元共计5 210 个，节点4 925 个。吊杆和主梁通过刚性连接连接，主拱与主梁、边拱与主梁通过弹性连接的刚性加刚性连接来模拟刚接效应。

所建立的全桥三维有限元模型见图2。

图2 全桥模型三维视图

本次检测主要依据JTG/T J21—2011 公路桥梁承载能力检测评定规程开展相关计算工作，通过对桥梁进行的静力荷载试验，测定结构关键控制截面及关键构件在试验荷载作用下的响应，然后与有限元理论计算值进行比较，进而判断结构的受力性能是否满足预期。

2．3 检算评定方法

其承载能力极限状态主要依据下式进行计算评定。

γ0S≤R(fd，ζc，adc，ζs，ads)Z2(1 －ζe) 。

其中，γ0为结构的重要性系数；S为荷载效应函数；R（） 为抗力效应函数；fd为材料强度设计值；adc为构件混凝土几何参数值；ads为构件钢筋几何参数值；Z1为承载能力检算系数；ζe为承载能力恶化系数；ζc为配筋混凝土结构的截面折减系数；ζs为钢筋的截面折减系数。

2．4 检测实验荷载的确定

就结构的具体某一测试内容，推算所需加载车辆的数量，也就是根据设计标准活荷载产生的在该结构构件最不利响应值，按下式所确定的原则进行等效换算。

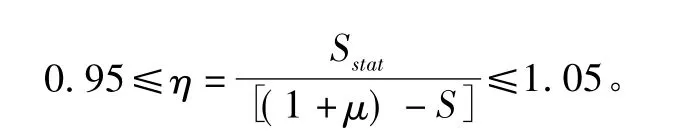
其中，η为静力试验荷载加载效率；Stat为试验荷载作用下，结构某一加载构件对控制截面内力或变位等的最大计算效应值；S为设计标准活载不计冲击荷载作用时产生的该加载构件对应的控制截面内力或变位等的最不利计算效应值；1 +μ为设计计算冲击系数。

按照上述加载原则，得到检测荷载布置情况如图3所示。

2．5 检测荷载布置追踪

通过有限元程序的荷载追踪功能，针对主跨拱肋左拱脚轴力最大和最小、主跨拱肋格右拱脚轴力最大和最小、主跨拱肋拱顶弯矩轴力最大和最小6 种情况对检测荷载布置位置进行追踪，得到各个情况下检测荷载的布置位置，分别见图4 ～图9。

图4 左拱脚轴力最大时检测荷载布置图

图6 右拱脚轴力最大时检测荷载布置图

图7 右拱脚轴力最小时检测荷载布置图

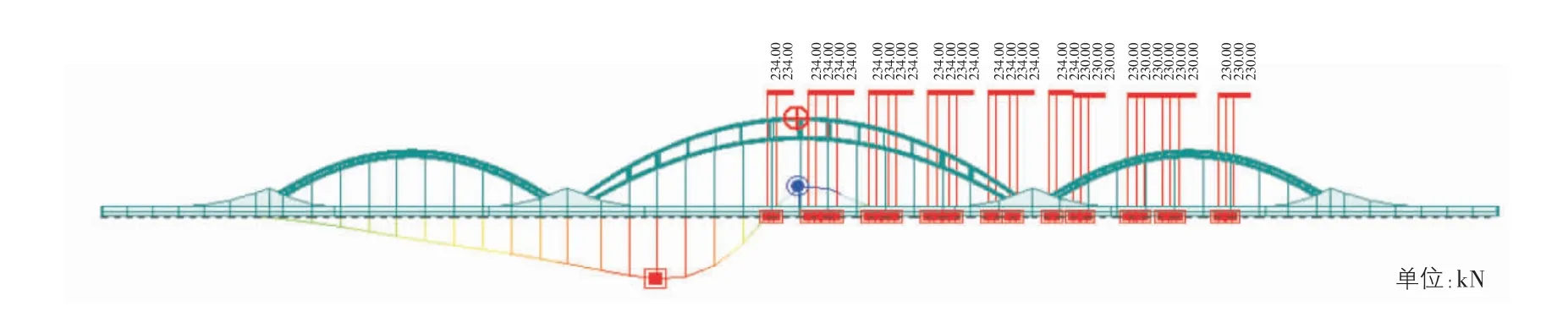
图8 拱顶弯矩最大时检测荷载布置图

图9 拱顶弯矩最小时检测荷载布置图

针对空间有限元模型［7］，追踪的单位编号如表1所示。

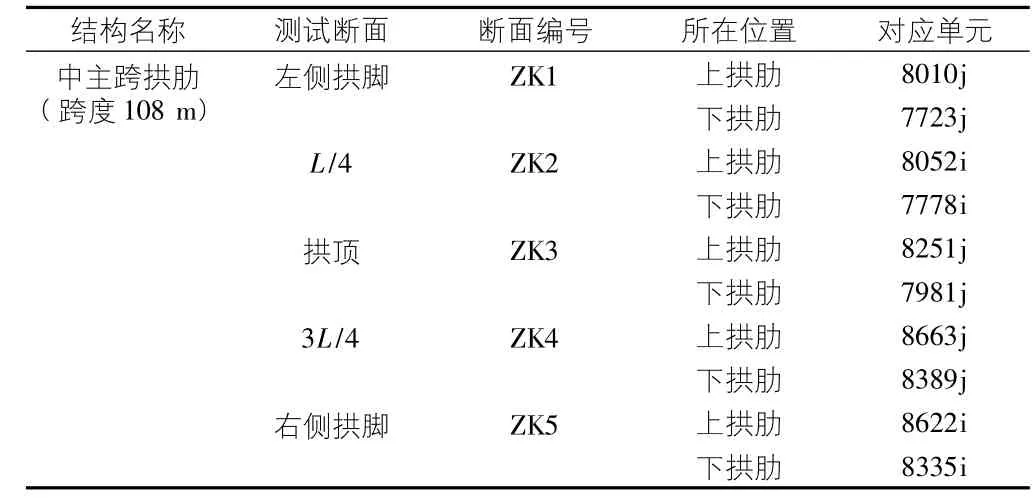
表1 对应有限元模型单元位置

2．6 计算结果分析

按照上述6 种荷载布置形式，分为6 个工况对结构进行理论分析，此处仅取中跨跨中拱肋截面上下缘的受力情况进行分析计算。并且将理论计算结果和实测结果进行比对，进而分析结构的承载能力变化情况和现有服役状态，内力理论计算及实测结果及二者对比情况如表2 所示。

表2 各工况下中跨拱肋主拱圈截面理论及实际效应对比表

支座位移理论计算及实测结果和二者对比情况如表3 所示。

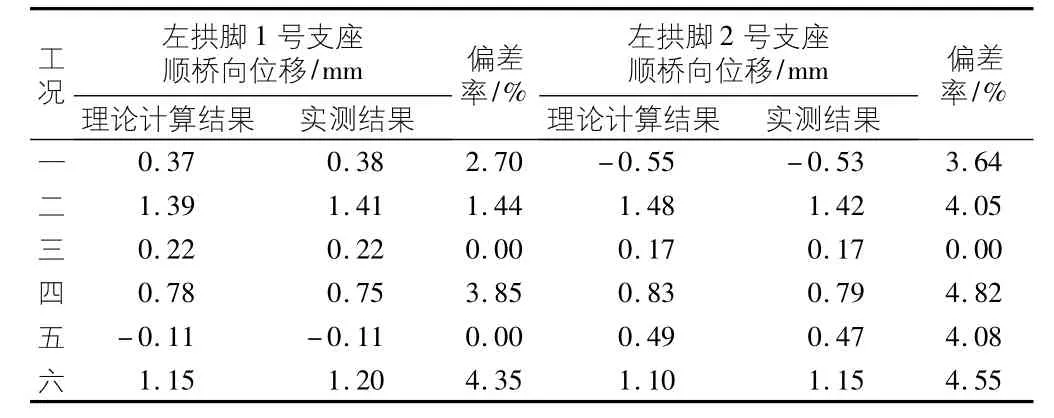
表3 支座位移理论计算及实测结果对比表

由结果可知，在6 种不同的工况下，通过对跨中拱肋轴力及应力的计算得到的理论数据，与静载试验得到的实测数据高度吻合，其误差在±5%以内，说明大桥运营状况良好，运营期间各个构件损伤较小，不需要进行大的维修及加固［8－10］。

由结果又知，在6 种不同的工况下，支座位移理论计算值和实测值吻合也较好，其误差也在±5%以内［11－12］。

3 结论与建议

通过对背景桥梁进行荷载试验，并且通过试验结果与理论值的对比分析可得如下结论：

1） 实测结果和理论结果的对比，实测结果和设计理论结果吻合较好，说明该桥梁运营状况良好。

2） 有限元程序的发展，使得基于荷载试验的桥梁评价变得十分方便，可以更容易得到结构控制截面某内力为极值时检测荷载的布置形式，进而指导现场静载试验的车辆布置形式，同时快速得出结构的理论反应数值并和实测结果进行比较。

荷载试验理论计算需要注意以下几点：

1） 区别于设计，荷载试验都是静载试验，所以在有限元程序计算时务必忽略冲击系数的影响，否则理论计算结果会有很大偏差。

2） 本文仅仅为了说明问题，仅对一个截面的结果进行了计算和比较，实际工作中，结构的关键部位和截面按照实际情况，选择越多越好，以降低人为因素引起的误差甚至错误。

3） 对一定服役期限的桥梁，应该结合实际运营情况进行某些系数的折减，比如预应力的松弛，混凝土的老化等。

4） 参数的折减应该结合结构所处的实际位置以及实际服役期限进行，必要时需要通过实验手段得到相关参数。