分布式光伏储能系统的优化配置方法
2022-03-17郑连清郑天文
彭 伟,郑连清,郑天文
(1.输配电装备及系统安全与新技术国家重点实验室(重庆大学),重庆 400044;2.清华四川能源互联网研究院,四川 成都 610213)
0 引 言
随着化石能源危机与环境污染问题日益严重,建设清洁低碳、安全高效的能源体系已是未来发展的必然趋势,太阳能资源作为一种清洁可再生能源目前已广泛应用于分布式光伏发电系统[1]。
光伏发电的随机性和间歇性导致输出功率波动较大,为电网的安全稳定运行带来严重挑战。同时随着需求侧负荷峰谷差增加,负荷尖峰时刻供电问题更加凸显,单纯的增加发电机备用容量不仅投资费用昂贵而且设备资源利用率低。储能具有功率快速控制、能量灵活吞吐的特性,是当前解决光伏并网和消纳的有效手段之一[2]。目前储能投资费用是制约其推广应用的关键,因此研究储能的优化配置对于提高光伏消纳、电网稳定和系统经济效益都具有重要意义。
目前,国内外许多学者对此课题进行了广泛研究,储能优化配置方法主要有差额补充法、波动平抑分析法和经济性评估法。1)差额补偿法:文献[3]介绍了在光伏-储能系统中利用光伏发电系统的最小日发电量与其在雨雪等极端天气下的发电量差额作为储能的配置容量;文献[4]根据风速概率密度计算风电场输出功率期望值作为风电场平均功率水平,用实际输出功率和该平均功率的差额确定储能的补偿容量,可实现风电场的定功率输出,但储能容量相对要大一些。2)波动平抑分析法:文献[5]介绍了一种基于平滑控制的超级电容与电池混合储能系统的能量管理方法;文献[6]提出了一种用于控制微电网联络线功率输出的储能系统容量优化方法;文献[7]通过BESS所需补偿特定频段来确定其功率容量,但补偿频段的选取仅限于0.01~1 Hz之间,适应性不强,且没有给出储能系统容量确定方法。3)经济评估法:文献[8]介绍了储能配置在光伏发电侧从减小脱网考核、限电考核和功率控制子站投运率考核等几方面衡量储能的经济效益;文献[9]以并网分布式光伏储能系统作为研究对象,配置储能后系统运行最小电力花费为目标;文献[10-11]针对储能系统利用分时电价峰谷价差套利、参与辅助服务、替代备用电源等,建立了系统收益目标函数,使配置储能后系统收益最大。
已有的储能优化配置研究中经济评估法使用较少,且研究对象多为单一分布式电源中配置储能。因此,考虑在分布式光伏储能系统中针对多个分布式源配置储能建立双层优化模型,外层采用遗传算法优化储能配置位置、功率和容量,内层采用粒子群算法结合MATPOWER[12]潮流计算工具优化储能日内运行策略使系统总成本最小;最后,在Matlab软件中采用改进IEEE9节点系统验证了优化配置方法的可行性和有效性。
1 分布式储能系统优化配置模型
考虑在分布式光伏储能系统中针对多个分布式电源配置储能,采用经济评估法对不同储能配置方案进行评价,最终取经济性最佳方案作为储能最优配置方案。
1.1 目标函数
取储能系统年总成本作为目标函数,主要包括电网网损费用、分布式电源提供的无功功率费用、储能充放电费用以及储能成本费用,具体公式如式(1)所示。
F=CLOSS+CDG+CPB+CDESS
(1)
式中:F为储能系统年总成本;CLOSS为网损费用;CDG为分布式电源提供的无功功率费用;CPB为储能充放电费用;CDESS为储能成本费用。
(2)
式中:PLOSS(i)为采样时刻电网损耗功率;Δt为系统采样时间间隔;R(i)为分时电价;T为一年内储能系统运行天数。
(3)
式中,Pdg(i)为采样时刻分布式电源提供的无功功率。
(4)
式中:Pch(i)为采样时刻储能电池的充电功率;Pdis(i)为放电功率。
CDESS=CBESS+CM
(5)
式中:CBESS为储能系统投资建设费用;CM为储能运行维护费用。
(6)
式中:Pbess为储能配置功率;Ebess为配置容量;Cp为储能单位功率成本;CE为储能单位容量成本;r为贴现率;n为储能系统寿命年限;m为储能安装个数。
CM=CmQ
(7)
式中:Cm为单位发电量储能运行维护成本;Q为储能装置年发电量。
1.2 约束条件
约束条件考虑了电网安全性和储能系统运行稳定性,具体包括:电网节点功率平衡约束、分布式电源出力约束、节点电压幅值约束、支路有功功率约束、储能系统充放电功率约束以及荷电状态约束等。
1)节点功率平衡
(8)
(9)
式中:Pit、Qit分别为t时刻电网节点i的注入有功功率和无功功率;Uit、Ujt分别为t时刻节点i、j的电压;δit、δjt分别为t时刻节点i、j的相角;Gij、Bij分别为节点导纳矩阵第i行j列的实部和虚部;N为节点总数。
2)发电机出力约束
Pr,min≤PG,r,t≤Pr,max
(10)
式中,Pr,min、Pr,max和PG,r,t分别为第r个分布式电源的最小、最大出力和t时刻第r个电源的实际出力。
3)节点电压约束
Ui,min≤Ui,t≤Ui,max
(11)
式中,Ur,min、Ui,max和Ui,t分别为节点i所允许的最低、最高电压和t时刻节点i实际电压。
4)支路有功约束
-Pl,max≤Pl,t≤Pl,max
(12)
式中:Pl,max为支路l的最大有功功率;Pl,t为支路l在t时刻的实际有功功率。
5)储能荷电状态连续性约束
(13)
式中:Soc,x,0和Soc,x,t分别为储能系统x的初始时刻和t时刻的荷电状态;Pch,x和Pdis,x分别为储能系统x的充放电功率;ηc,x和ηd,x分别为储能系统x的充放电效率;Ebess,x为储能系统x的额定容量。
6)储能荷电状态约束
Soc,min≤Soc(i)≤Soc,max
(14)
式中,Soc,min和Soc,max分别为储能系统x的最小和最大荷电状态。
7)储能系统功率约束
PDESS,i,t=xi(Pdis,i,t-Pch,i,t)
(15)
式中:PDESS,i,t为节点i处储能在t时刻的实际充放电功率;xi为0—1状态变量,1表示电网第i个节点位置接入储能,反之未接入;Pdis,i,t为节点i储能t时刻放电功率;Pch,i,t为节点i储能t时刻充电功率。
8)储能系统充放电功率约束
-Pbess≤Pdis,i,t≤Pbess
(16)
-Pbess≤Pch,i,t≤Pbess
(17)
式中,Pbess为第i个节点接入储能的额定功率。
2 储能优化配置求解方法
2.1 求解流程
分布式储能优化配置是一个多目标非线性整数规划问题,包括确定储能接入位置、功率、容量以及运行策略等。将单层多目标优化问题转换为双层优化来求解,可以很大程度降低求解复杂程度。因此,建立双层优化模型:外层优化目标为储能系统接入位置、功率和容量,以上技术参数为离散整数形式,适合采用遗传算法基因编码优化求解;内层优化目标为储能系统成本,在外层给出确定的储能参数后,内层采用粒子群算法结合MATPOWER潮流计算工具,优化储能系统的运行策略,使储能系统在该种配置下总成本最小;然后,将内层优化结果反馈回外层进行遗传算法的选择、交叉和变异运算,通过反复迭代比较确定可行域内储能最优配置和运行策略。具体求解过程如储能优化配置流程图1所示。
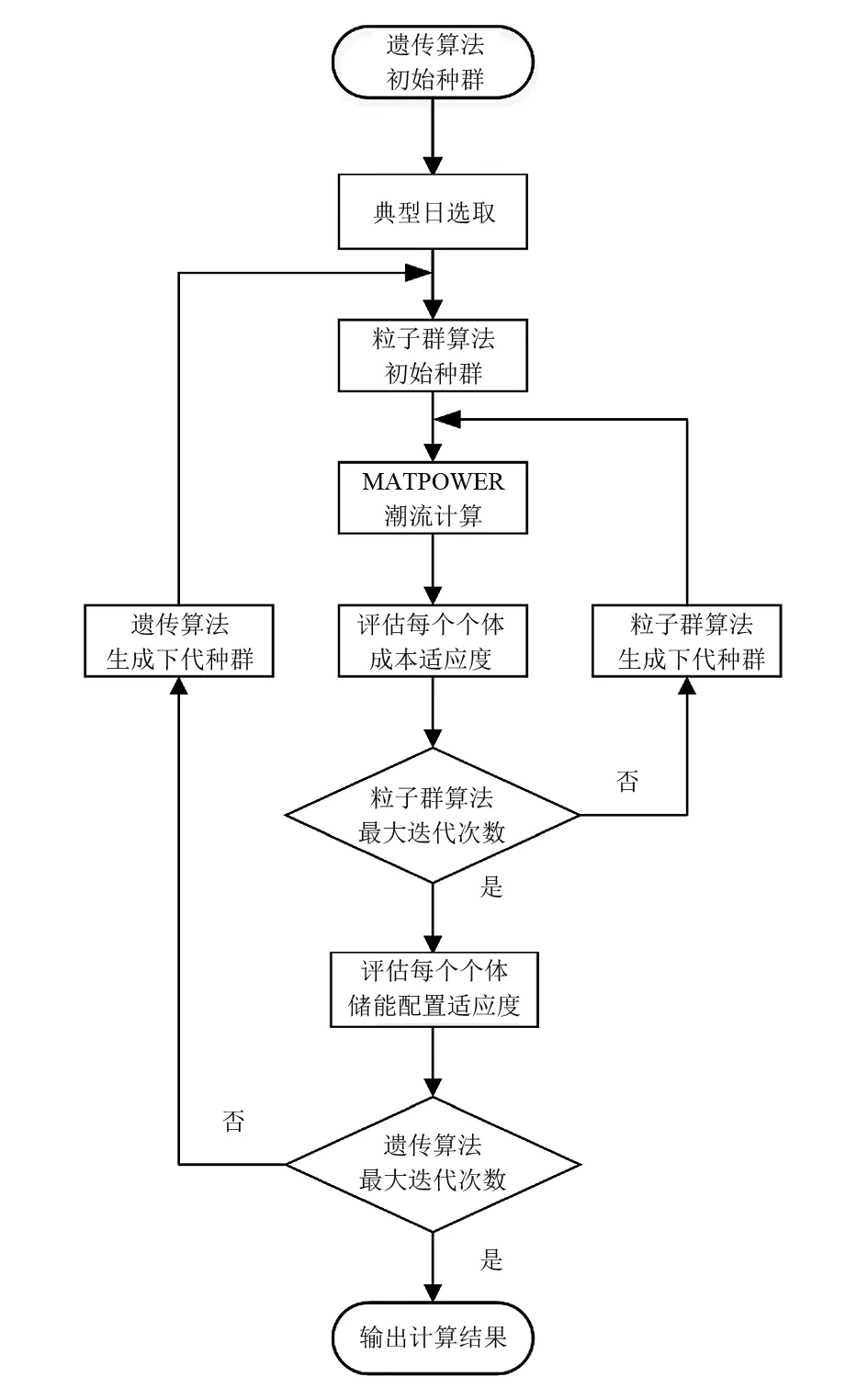
图1 储能优化配置流程
2.2 遗传算法
遗传算法(genetic algorithm,GA)是模拟自然界生物进化机制的一种算法。首先,需要通过编码建立一个初始种群;然后,运用遗传操作对种群中每个个体对环境的适应程度进行操作,实现优胜劣汰的进化过程。
种群中的个体编码信息包含影响目标函数的决策变量,类似于决定生物特性的基因,同时遗传算法中个体信息采用二进制编码,适合于表示离散整数变量。文中的种群个体信息包含储能接入位置、功率和容量等信息。
遗传算法的目标函数为F,在确定种群后每个个体将信息传递给内层优化,通过粒子群算法得到的优化结果即为该遗传个体的适应度。根据每个个体的适应度筛选出优质个体保留到下一代,直至求得最优解。其中遗传操作主要包括选择算子,交叉算子和变异算子。
2.3 粒子群算法
粒子群算法(particle swarm optimization,PSO)也是一种进化算法,适用于解决连续非线性问题。它是从随机解出发,通过迭代寻求最优解。优化问题的每个潜在解都可以看作一个粒子,每个粒子都有一个适应度(fitness),由自身参数和与目标函数映射关系决定;粒子包含速度和位置两个参数,前者决定粒子飞行的速度和方向,后者表示目标的一种潜在解。采用线性递减权重控制策略(linearly decreasing weight,LDW),能够有效提高算法寻优速度,具体公式如下:
vij,k+1=ωvij,k+c1r1(pbij,k-xij,k)+
c2r2(gbj,k-xij,k)
(18)
(19)
xij,k+1=xij,k+vij,k+1
(20)
式中:i为第i个粒子;j为粒子的维度;k为迭代次数;ω为权重系数;pb为个体极值;gb为全局极值;c1、c2为学习因子;r1、r2为0~1之间的随机数;ωini为初始权重;ωend为迭代至最大进化代数时的权重;xij为粒子的位置。
在外层优化给定储能接入位置、功率和容量后,内层首先随机产生各采样时刻储能的充放电功率;然后,根据储能荷电状态连续性约束进行功率修正并得到单个个体日内运行策略;最后,利用粒子群优化算法结合MATPOWER潮流计算工具通过多次迭代寻优求得当前给定配置下储能系统的最优日内运行策略。
3 算例分析
3.1 参数配置
选取改进IEEE 9节点系统作为仿真测试算例,图2为系统电气接线图,其中2号、3号节点分别接入最大出力为16.5 MW和8.3 MW的光伏发电系统,1号节点为系统平衡节点且接有装机容量为30 MW的常规发电机组,5号、7号和9号节点处接入负荷。
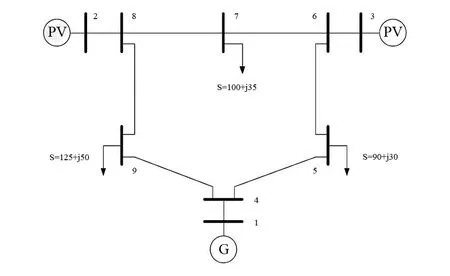
图2 IEEE 9节点电气接线
现考虑在1—9号节点中最多选取2个位置配置储能,储能额定功率可选4.0、6.0、8.0、10.0 MW,额定容量可选4~50 MWh。
图3为2号光伏发电系统某典型日出力曲线图,其中采样时间间隔为1 h。为简化计算,3号光伏发电系统各时刻出力取为2号光伏发电系统同时刻出力的0.5倍。
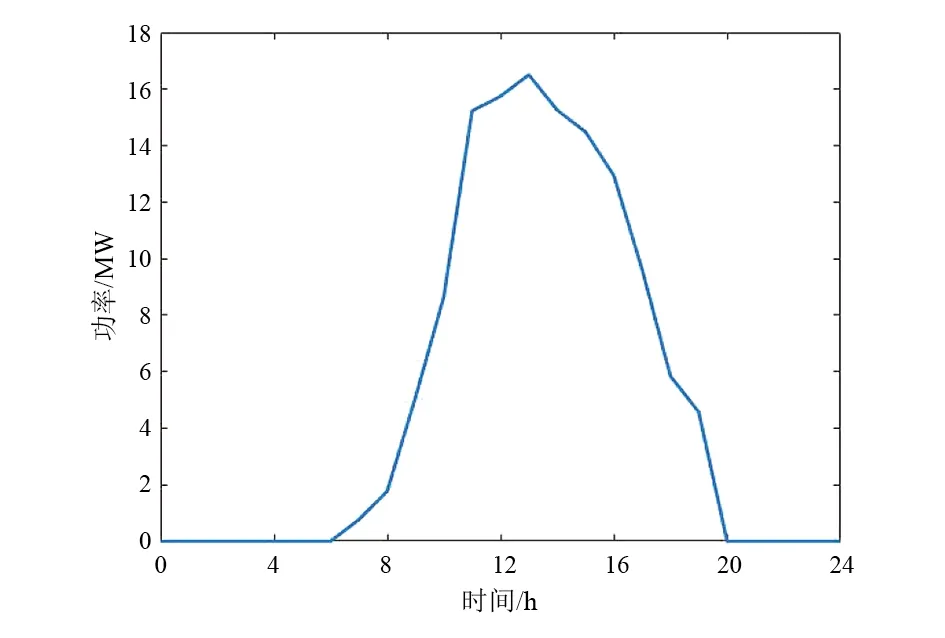
图3 光伏出力曲线
选取中国某地区分时电能表,其峰谷电价执行时段和具体价格如表1所示。储能电池选择综合性能较好的锂离子电池,它支持深度充放电,在80%的放电深度情况下循环寿命可达3000次以上,仿真相关参数选取如表2所示[13-16]。
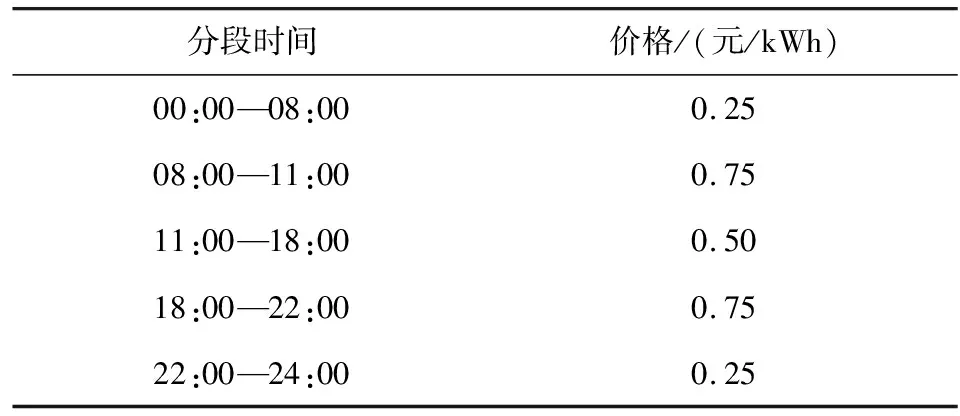
表1 分时电价
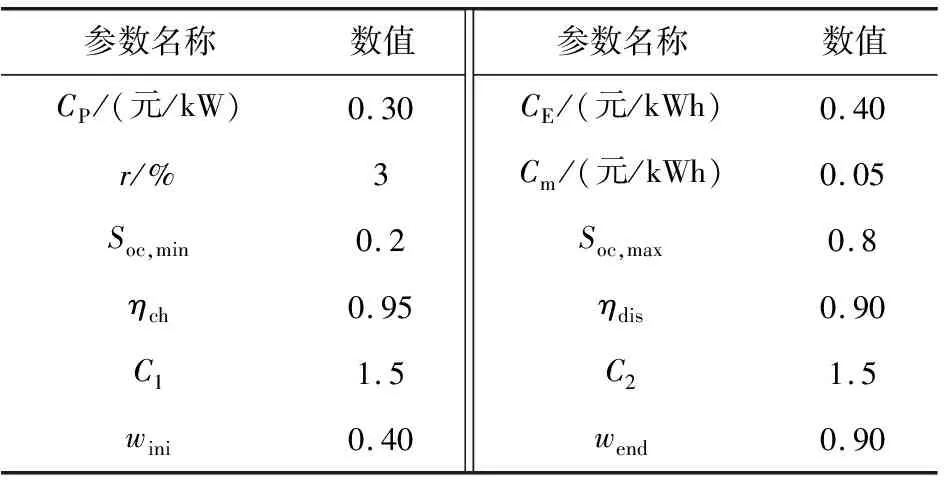
表2 工程参数
3.2 结果分析
按照双层优化模型求解流程,在外层遗传算法最大迭代次数100次、交叉率0.7、变异率0.05,在内层粒子群算法最大迭代次数100次、种群数60的情况下通过运行程序解得储能最佳配置方案为:4号和9号节点分别接入4 MW/4 MWh电池储能。
图4为分布式储能系统总成本随迭代次数的变化曲线,可以看出当迭代次数达65次时目标收敛,此时系统最小成本为4225万元/年。图5和图6分别为系统取最小成本时,4号和9号节点处储能的荷电状态曲线。
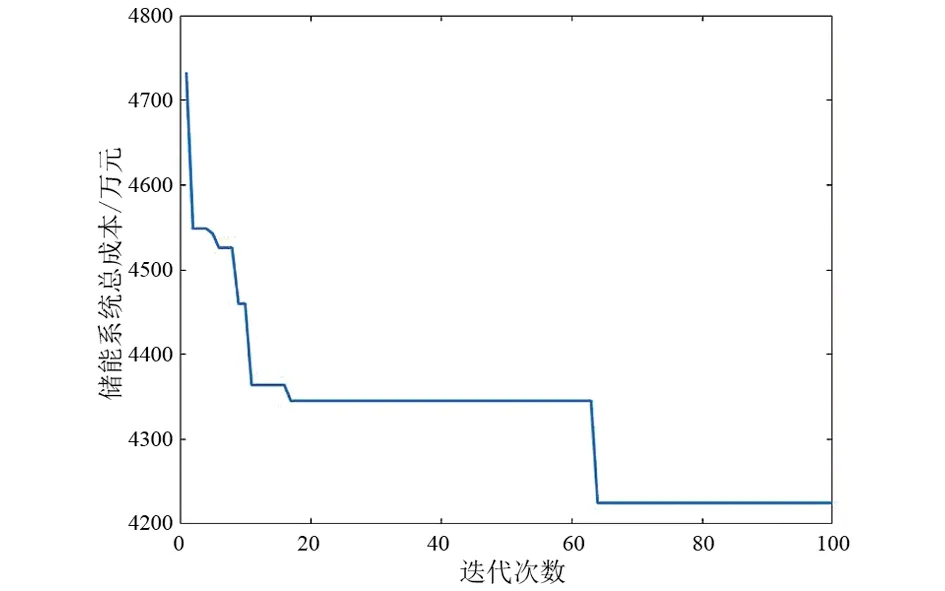
图4 储能系统成本适应值曲线
从图5和图6可看出储能主要在00.00—08:00和11:00—18:00电价低平时段充电,08:00—11:00和18:00—22:00电价峰值时段放电,储能运行策略能够利用峰谷电价差套利减小充放电费用。
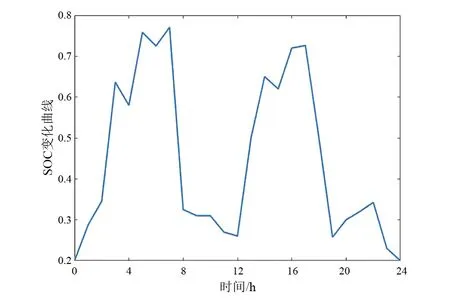
图5 4号节点储能SOC曲线
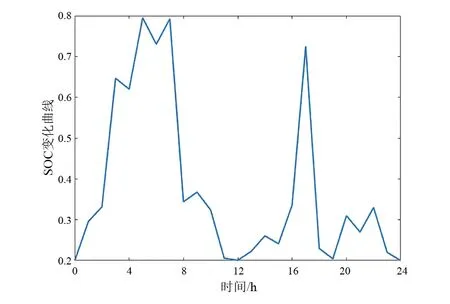
图6 9号节点储能SOC曲线
4 结 论
针对分布式光伏储能系统优化配置问题,提出遗传算法结合粒子群算法的双层优化模型。详细介绍了算法求解流程,然后通过改进IEEE9节点系统进行仿真验证,最后得到了以下基本结论:
1)所提出的双层优化模型能够有效解决分布式光伏系统中储能选点布局和容量配置问题,同时算法运行稳定且收敛性良好。
2)在给定的IEEE9节点系统中,当4号节点和9号节点分别接入4 MW/4 WMh的储能时,系统最小成本为4225万元/年。
3)储能运行策略主要表现为:电价低平时段充电,峰值时段放电,通过峰谷电价差套利减小充放电费用;同时储能不同时刻的充放电能够改变电网潮流,一定程度上降低系统网损和无功费用。
