基于小波包能量的漏电保护方案研究
2022-03-17左金威
赵 恒,左金威,瞿 科
(1.国网四川省电力公司,四川 成都 610041;2.四川大学电气工程学院,四川 成都 610065)
0 引 言
低压配电网作为电力传输终端,直接面向电力用户,而因触电事故造成的人身伤害和经济损失成为工业界和学术界关注的重要问题。目前低压配电网主要采用剩余电流保护装置,在发生触电的情况下切除电源从而保障人身安全[1]。漏电保护器根据动作类型分类,可分为电磁式和电子式[2];漏电保护器根据对含有直流分量漏电流的不同动作特性,可以分为AC型、A型和B型[3]。但是这些漏电保护器主要根据触电以后剩余电流大小或变化量动作,不能有效区别生命体和非生命体触电,降低了对人身安全保护的动作正确率。由于运行、测量噪声等多因素的影响,生命体触电特征监测分析亟待解决。研究生命体触电事故检测方法和开发有效漏电保护方案对于保护人身安全,降低事故损害具有重要的理论价值和工程意义。
近年来,国内外学者对触电事故特征检测分析开展了相关研究,主要包括时频域分析[4-7]和数字滤波分析[8-9]。文献[4]对不同的生物触电模型提取了多个时域和频域特征,通过降维处理和支持向量机进行触电识别。文献[5]提出识别生物触电电流改进型近似熵的计算方法,减少了计算量,缩短了判断时间。文献[6]利用傅里叶变换和弗莱贝尔格等值模型计算生物阻抗特征,展现了触电的暂态过程;文献[7]利用快速傅里叶变换对生物触电电流进行了频谱分析,得到了生物触电电流和总剩余电流相关的结论。文献[8]将基于有限冲击响应的数字滤波技术与径向基函数神经网络技术结合,实现了快速识别触电事件。文献[9]结合滤波算法和S变换,从时频特征和能量变换不同角度,对比分析触电和非触电信号,提出了识别生命体触电的特征量。生命体与非生命体之间存在明显的阻抗特征差异,生命体阻抗特性复杂,频散特性是区分生命体触电和非生命体触电的有效特征[10-11]。但是该算法难度大,且需系统存在谐波分量,实际应用困难。
相对熵可以衡量两个随机变量之间的距离。小波包相对熵分析方法,集中了小波包和相对熵的优点,小波包放大局部信号,能够根据信号的特点自适应地选择频带,而相对熵能反应信号之间的细微差别,相对熵越大,信号变化越大[12-14]。用电阻、猪肉和活兔进行单相触电实验,以保护装置检测所得单通道故障剩余电流为检测电流,从时域、频域进行生命体触电特征的提取,并在此基础上设计基于小波包能量相对熵的漏电保护方案,通过实验验证相对熵作为生命体触电特征的有效性。
1 生命体阻抗模型与触电特征分析
1.1 生命体Cole-Cole模型
生物组织电特性广泛被运用于人体成分和病理学研究[15]。由于构成人体组织的细胞和细胞间质具有不同的电特性,人体组织具有电容特性,低频时高阻抗,高频时低阻抗。如图1所示,1940年科尔提出了贴合生物组织阻抗特性的模型[16],其中Rs和Rb为生命体组织等效电阻,Cs为依赖频率的等效电容。

图1 生命体等效模型
1.2 时域特征和频域特征
时域特征根据实际触电电流,利用统计量进行分析,包括均值、方差、偏度和峭度[17]。选取均值和方差来度量触电特征。
设有限长的随机信号为x(n)={x1,x2,…,xn},统计量均值μx的计算公式为
(1)
式中:E为期望值;μx为均值;N为信号总长度。
方差用于表示随机信号偏离其平均值的程度,计算公式为
(2)
频域特征主要利用傅里叶变换将信号从时域转换为频域,得到各频域的幅值和能量分布情况,便于对信号本质进行更深的挖掘。
2 基于小波包能量相对熵触电识别
2.1 小波包能量相对熵原理
近年来,信息理论在电力系统分析诊断中得到越来越广泛的应用,其中相对熵可以衡量两个随机变量之间的变化情况。当两个随机变量分布相同时,它们的相对熵为0;当两个随机变量的差异越大时,它们的相对熵也会变大。对于信号而言,信号变化程度越大,相对熵越大。
小波包分解通过高低通滤波器,将两个分量重复计算达到分辨率要求,其公式为
(3)
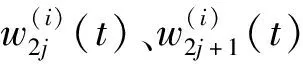
通过对信号w(t)进行i层分解,得到第j频段的能量为
(4)
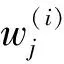
该频段能量在总能量中比例为
(5)

(6)
式中,k为小波包分解层数。
2.2 小波包能量相对熵识别流程
现有漏电保护器一般通过总剩余电流或者故障剩余电流幅值进行动作。因正常剩余电流与故障电流之间相角的不确定性,总剩余电流可能增大也可能减小,基于总剩余电流动作的漏电保护器可能拒动或误动;同时由于现有漏电保护器不能有效识别生命体触电,基于故障剩余电流动作的漏电保护器阈值低(30 mA),导致动作频繁,在广大的农村地区投运率低,触电伤亡事件时有发生。
新型漏电保护器设计以识别生命体触电为核心,在现有漏电保护器的基础上改进为3个识别环节。包括总剩余电流动作、故障剩余电流动作和人体触电识别动作3个环节,如图2所示。

图2 小波包能量相对熵识别流程
一个周期的波形数据采集n个采样点数据,将第i个电流采样点数据记作Ii,命名为I1、I2…In进行下面的分析整定。
步骤1:为避免较大泄漏电流长期存在,首先进行总剩余电流幅值判断,记为|I|。
(7)
式中:Ii为第i个采样点电流;n为一个周期采样点数。
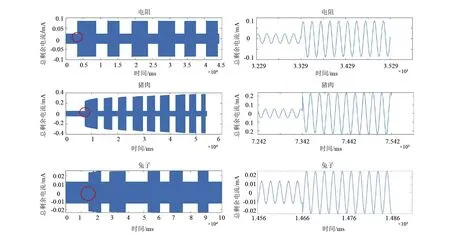
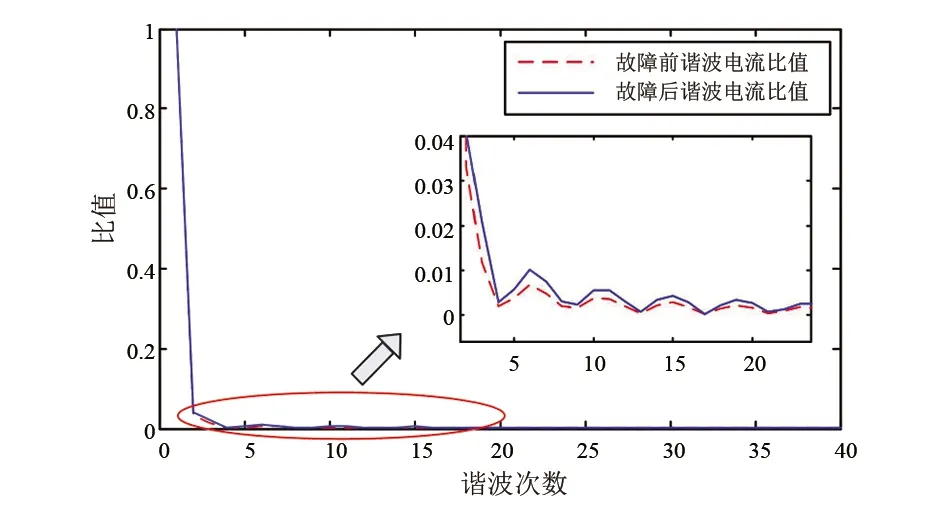
如果|I|≥Irp,则判定线路有故障发生,长延时后,继电器切断回路;如果|I| 步骤2:判断故障剩余电流。根据式(7)计算出总剩余电流前后2个周波的矢量变化量有效值,记为|ΔI|。 (8) 若|ΔI|≥20 mA,则进入下一环节判断,若不成立,则返回步骤1;如果有|ΔI|≥ΔIrp,则判定有故障发生,短延时后,切断主回路;如果有|ΔI|<ΔIrp,则判定无故障发生,动作机构不动作,返回到步骤1。其中,ΔIrp为剩余电流变化量整定值。因有第三环节的人体触电识别保护,ΔIrp可根据运行状况在20~100 mA设定,为避免频繁跳闸此处设定为50 mA。 步骤3:对于生命体触电识别动作,进行小波包能量相对熵R计算,若小于阈值,则不动作,返回步骤1;若大于阈值,识别为生命体触电,则无延时动作,继电器切断主回路。 通过对100余组猪、兔触电故障电流小波包能像能量相对熵进行计算,选取db5小波,进行3层小波包分解,阈值R为0.01。 为获取真实的生物触电信号,搭建了生物触电实验平台。FLUKE 6100 A标准扰动源提供电源信号;功率放大器将电源信号放大至可带功率的电压信号;采用YOKOGAWA DL750示波录波仪对相关电流、电压信号录波;3盏白炽灯(220 V,50 Hz,100 W)模拟线路负载,触电实验接线图如图3所示。 图3 触电实验接线 Ih、If、Il分别为总剩余电流、漏电故障电流、正常剩余电流,系统电压为UA,负载电流为IA,触电物体的两段电压为Uf,故障支路RA、RN和CA、CN分别表示单相线路对地绝缘电阻和对地分布电容,RC为故障支路接触电阻。 FLUKE 6100 A输出电压源为:50 Hz基频,0~20次谐波,基波为10 V;功率放大器输出:220 V;DL750采样频率:10 kHz;接触电阻Rc为8000 Ω。分别以一个4000 Ω电阻、新鲜猪肉、活兔为实验对象,获取实验数据。兔子作为实验对象的时候,以兔子的左前肢和右后肢为触电接触部位,并接入接触电阻Rc。为了确保能够有效模拟人体皮肤,实验做了以下处理:1)电极贴片包裹兔子的触电接触部位并用多股铜线芯缠绕,避免增大接触阻抗;2)保持兔子触电接触部位的皮肤完整不破损,确保皮肤阻抗正常;3)将兔子触电接触部位的毛发清理干净,避免毛发的绝缘作用。为了保证不对兔子造成致命的伤害,实验时将对兔子麻醉并加入接触阻抗。 根据图3搭建了试验电路,利用电阻、新鲜猪肉和活兔进行触电实验,分别得到触电波形如图4所示。 图4 电阻、猪肉、活兔触电总剩余电流 从上述波形可以看出,因为有对地电容的存在,在故障发生前,总回路中存在一定的剩余电流。在故障发生后,3组实验剩余电流均增大,对比3组图形可以看出:1)猪肉和兔子故障后,剩余电流存在一个明显的暂态过程,之后趋于稳定。2)电阻触电故障后,剩余电电流增大幅度是固定的,表现出线性特征;而兔子和猪肉触电故障后,剩余电流持续增大,呈现明显的非线性特征。分别从时域和频域进行特征分析。 从剩余电流均值统计(见表1)可以看出,触电后,猪肉、兔子的剩余电流在不断增大,但增幅并不明显,20个周波中平均增幅分别为0.199 4%,0.013 8%,而电阻增幅趋于0。说明由于生命体细胞中存在电阻和电容,在触电过程中,电流的热效应和化学效应对生命体带来损伤,生物阻抗随时间增加而变化,生物的触电电流随时间增加而增大。同时由于接触面积等触电实际情况不同,猪肉和活兔的电流增幅不同。从剩余电流方差统计(见表2)可以看出,电阻变化率趋近0,猪肉和活兔分别偏离平均值0.389 6%和0.028%,方差在触电后20个周期内呈现增长的趋势,但增长幅度仍然很小。 表1 剩余电流均值统计 表2 剩余电流方差统计 从上述可以看出,生物在触电过程中存在触电电流幅值递增的非线性的触电特征,但增幅绝对值较小,猪肉和活兔的周期平均变化阈值为10-3mA,且变化尺度不一。利用时域特征进行漏电保护器开发还存在两个方面的问题:1)短时间尺度下特征无法提取。中国规定漏电保护器最大分断时间为200 ms,人体安全电流小于30 mA。在短时间内,设定小电流低变化率的特征阈值,对测量设备的精度提出较高要求,而长时间尺度下,动作时间不能满足人体安全保护的要求。2)配电系统本身运行工况复杂,扰动较多,绝缘老化、天气潮湿等故障具有相似特征,利用幅值递增进行判断很难区别生命体和非生命体触电信号,容易出现误动。 频域特征主要利用傅里叶变换将信号从时域转换为频域,得到各频域的幅值和能量分布情况。图5为猪肉触电试验总剩余电流故障前后频谱波形图,图6为猪肉触电试验各次谐波与基波比值曲线。故障前的谐波总畸变率为3.7%,故障后的谐波总畸变率为4.9%。对比各次谐波的成分,故障后的低次谐波含量较故障前的低次谐波含量更高。可以看出故障前后,电流差异大,由于受生命体阻抗特征的影响,呈现出非线性的变化,在不同频率下的能量分布不同。 图5 猪肉触电试验总剩余电流故障前后频谱波形 图6 猪肉触电试验各次谐波与基波比值曲线 利用小波包能量相对熵进行触电特征识别,因采样频率为10 kHz,在触电前后各取4个周期数据(T1—T8),选取db5小波,进行3层小波包分解,相邻周期对应计算小波包能量相对熵,其结果如表3和图7所示。从计算结果可以看出: 表3 小波包能量相对熵统计 图7 小波包能量相对熵曲线 1)触电前4个周期(T1—T4)的小波包能量相对熵无明显变化,信号几乎相同;但触电后,从周期T5开始,猪肉和兔子的熵值呈现明显增长,而电阻的熵值变化不明显,说明生命体触电后,由于受生命体阻抗特点的影响,触电电流频谱发生明显变化,复杂程度增大。 2)在触电后的2个周期T5,T6内,猪肉和兔子熵值变化存在明显暂态过程,相对熵均大于0.01,可以识别为生命体触电,并在2个周期后趋于稳定。 从以上实验可以看出,通过小波包能量相对熵的计算,滤除了电流中谐波的影响,突出了生命体触电的主要特征,能够反映触电前后频谱的细微变化。 该算法只需采集2个周期电流,通过比较R≥0.01即可判断生命体触电。从时间上看,利用文中数据导入Matlab进行计算,第一环节剩余电流计算时间为8 ms,第二环节剩余电流变化量计算时间为12 ms,第三环节小波包能量相对熵计算时间为43 ms,计算判断时间为63 ms。同时数据采样时间2个周波为40 ms,机构动作时间一般为20 ms以内[19-20],总计时间为123 ms,能够满足200 ms的时间要求。 由此分析可知,小波包能量相对熵与剩余电流均值、方差和频谱特征相比,能够有效区别生命体和非生命体触电事故,可以用作漏电保护方案中触电识别的关键特征,进行软件功能设计。 前面提出了可通过检测并计算触电电流的小波包能量相对熵用于区别生命体和非生命体触电事故。同时搭建了物理实验平台,对生命体和非生命体触电进行模拟并获取实测数据,证明了所提的小波包能量相对熵识别生命体触电事故的有效性。在此基础上,提出了开发漏电保护器的方案。该方案简便可靠,符合漏电保护工程应用领域的要求。主要结论为: 1)在时域中,以猪肉和活兔为代表的生命体触电电流,触电后电流幅值持续增大,在2~4个周期后趋于稳定,表现出明显的非线性; 2)在频域中,以猪肉和活兔为代表的生命体触电电流,触电前后频谱发生畸变,触电电流能量主要分布在低频,高频能量较小且特征不明显; 3)小波包能量相对熵算法综合了小波包滤波以及相对熵识别细微特征的优点,与剩余电流均值、方差和频谱特征相比,能够有效区别生命体和非生命体触电事故,可以用作漏电保护方案中触电识别的关键特征,进行新型漏电保护器设计。3 实验数据验证分析
3.1 生命体触电电流获取

3.2 触电电流时域特征


3.3 触电电流频域特征

3.4 小波包能量相对熵


4 结 论
