面向细纱机多元性能退化过程的可靠性评估方法

邵景峰，董梦园,牛一凡,陈可心

(西安工程大学 管理学院，陕西 西安 710048)

0 引 言

准确评估纺织设备的工作状态，对于纺织行业充分利用生产能力、提高生产效率有着重要的意义。细纱机是是决定纱线质量的核心设备。细纱机作为一种大型复杂机电一体化设备，不仅内部结构复杂，涉及零配件和关键器材专件众多，而且具有高可靠性、长寿命等特点。如1台1 200锭的细纱机，涉及60多个关键器材专件、107 029个零件以及100多个温度、湿度、振动传感器。然而，细纱机在工作过程中受各种因素的交替作用和相互影响，致使其性能退化，这种退化又对成纱质量产生了严重影响。因此，如何对细纱机性能退化过程进行可靠性评估是一个亟待解决的问题。

对于细纱机性能退化的可靠性评估，目前多聚焦在细纱机的部分结构或细纱机的工艺参数评估。吴入军等从细纱机的部分组成结构入手，探讨牵伸机构中齿轮因磨损过大而损坏问题[1]，优化了细纱机的牵伸结构，提高了自身的可靠性；CUI等从牵伸系统的改进出发以提高成纱质量，研究了常规牵伸系统与改进型牵伸系统的不同之处，以及工艺参数对细纱机的影响[2]；HE等利用流体力学软件模拟和表征细纱机的运动，使纱线性能得到了提高[3]；LI等将可靠性增长系数与蒙特卡罗仿真模型相结合，建立了细纱机的可靠性评估模型[4]。目前已经解决了基于设备失效时间分析可靠性分布规律、建立可靠性指标以及故障频率的预测问题。

有的学者从细纱机内部故障角度入手，探讨细纱机运行状态的监控。文献[5]根据监控纺纱机的运行情况，实现了罗拉、钢领板和锭子等运动部件独立驱动的细纱机控制系统，提高了采集速率及数据传输的稳定性。众多的研究着眼于利用时域分析、小波变换和功率谱分析等方法实现细纱机正常运行与故障数据的采集；从零部件角度入手，探讨了细纱机故障辨识，已经解决了提取故障信息的特征参数的问题。宋晓亮等研制了一种光电反射式故障诊断器，解决了运动过程难以监控的问题[6]；王延年等利用改进神经网络的方法，降低了锭子转速波动，解决了细纱机锭子速度变化使细纱卷绕过程中断头率高的问题[7]。随着机电一体化技术的发展，学者们的研究聚焦在数据驱动的可靠性评估方面：通过建立复杂系统性能退化模型，对细纱机进行寿命预测和可靠性评估[8]。SI等利用Wiener 模型描述退化过程，并给出了对应的剩余寿命分布和可靠性函数解析形式[9]；LI等对随机过程中的维纳过程进行了深入的研究，推导并验证了模型中的随机参数[10]；赵广社等验证Wiener 模型，得到了较高的预测精度，为以后的研究提供了很好的理论基础[11]。

可见，人们的研究角度主要集中在细纱机运行数据采集以及部分结构的可靠性预测方面，忽略了设备在运行过程中的随机因素对设备使用寿命的影响，而且主要利用单一表征参数衡量设备退化轨迹，对多个指标的性能退化状态信息不能充分利用。此外，还存在如何充分利用监测到的信息对细纱机进行性能退化建模进而对可靠性进行评估问题，其中的瓶颈在于细纱机的关键性能参数难以识别以及性能退化模型难以建立。为此，本文提出一种面向细纱机多元性能退化过程的可靠性评估方法，为细纱机维修管理提供支持。

1 性能特征参数筛选

细纱机的性能退化过程常被视为一个随机过程[12]。在这个过程中，为了实现对细纱运行状态的监测，往往需要采集细纱机的许多传感器数据[13]。但问题是，因为其具有高维、随机性的特点，并非所有监测到的数据都能表征细纱机的性能变化。为了解决这一问题，引入主客观综合权重对细纱机的关键特征参数进行识别。具体过程如下：首先，利用序关系分析法[14]比较细纱机性能退化的特征参数的重要度，根据专家经验对参数重要程度排序，进而确定相邻两参数间的相对重要性，然后得到各个参数的权重系数pj。计算公式如下：

(1)

(2)

式中：pj为得到的第j个特征参数的权重值;pj+1为得到的第j+1个特征参数的权重值；yj为特征参数的重要度。但是，yj的计算结果易受主观因素的影响而产生偏离，故引入熵权法进行综合权重计算，具体的计算公式为

(3)

(4)

(5)

为了提高权重评价结果的准确性，利用最小二乘法，构建面向细纱机性能退化的指标权重ϖ，如式(6)所示：

(6)

式中：ϖj为待求的综合权重。在此基础上，选择综合权重大于0.5的参数，作为细纱机性能退化的表征参数，并将该参数应用于细纱机自身性能退化的全过程[15]。

2 多元参数退化过程统计分析

2.1 Wiener过程的性能退化建模

利用Wiener随机过程，对细纱机因自身磨损造成的性能退化过程加以描述[16]，构建的细纱机性能退化模型，如式(7)所示：

(t)=X(0)+μt+σβ(t)

(7)

式中：X(0)为初始性能退化量，通常设定X(0)=0；μ为飘移系数；β(t)为标准布朗运动；σ为扩散系数。设细纱机的寿命为T，失效阈值为ω，则细纱机的性能退化轨迹可由式(7)的Wiener过程进行描述。由此，细纱机的寿命T可定义如下：

T={t:X(t)≥ω|X(0)<ω}

(8)

由式(8)可知，细纱机寿命T达到失效阈值ω的时间服从逆高斯分布[17]：

(9)

(10)

式中：fT(t)为寿命T的概率密度函数；Rw(t)为细纱机单一过程的可靠性函数。

记ΔXi=Xti-Xtt-1,Δti=ti-ti-1。由Wiener过程的性质可知，细纱机性能退化增量之间相互独立，而且服从正态分布ΔXi～N(μΔti,σ2Δti)。于是，通过细纱机的性能退化数据，可得到似然函数：

(11)

通过式(11)，对漂移系数和扩散系数求偏导。令偏导为零并对方程求解，从而得到μ和σ2的估计值：

(12)

(13)

2.2 多退化过程的可靠性建模

Copula函数为求解基于多种退化过程的细纱机可靠度评估模型提供了便利条件。现假设细纱机的失效阈值为ωj，当第j个退化过程的退化量Xj(t)超过其对应的失效阈值ωj时，细纱机发生退化失效[18]。由此，细纱机性能退化过程对应的可靠性表示为

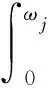
式中:f(Xj(t))为第j个退化过程对应的概率密度函数。在此基础上，进一步构建多元退化相关失效可靠性模型R′(t)，如式(14)所示:

(14)

为便于分析细纱机多元退化的相关性问题，利用Copula函数进行细纱机多元退化相关性的建模[19]。设细纱机的性能退化量为X1(t)、X2(t)，与其对应的性能退化函数为FX1(t)、FX2(t)，则{F(X1(t)),F(X2(t))}的联合分布函数可表示为

(15)

{F(X1(t)),F(X2(t))}的联合密度函数为

h(X1(t),X2(t);θ)=C(FX1(t),FX2(t);θ)·

fX1(t)fX2(t)

(16)

在常见的Copula函数形式中，选择合适的函数(t-Copula、 Gaussian Copula、 Clayton Copula、 Frank Copula、和Gumbel Copula)进行相关性分析。由于细纱机性能退化复杂，在相关性建模后变得更加复杂，而且未知参数较多。为此，利用基于贝叶斯理论的Gibbs算法[20]进行参数估计： 将2个过程所有的未知参数设为ξ，则ξ为一个n维向量，即ξ=(ξ1,ξ2,…,ξn)，对应的先验分布为p(ξ1,ξ2,…，ξn)。具体步骤如下:

3 实验验证

3.1 参数选择

可以通过直接分析细纱机在运行时的各种参数，如罗拉转速、锭子速度的变化表征细纱机的运行状态。比如，罗拉是细纱机上压住纱条或纤维的滚动长轴或短轴。罗拉速度不稳定，容易造成罗拉缠花，导致纱线断头，可以通过间接分析捻度平均值、管纱长度等成纱结果表征。又比如，细纱捻度不匀率过大会影响纱线单纱强力以及条干不均率，造成坯布布面黄白档等疵点，布面染色时会因为吸色性能差异而产生明显的色差等质量问题。

依托课题组在咸阳纺织集团安装的“纺织厂生产信息管理系统”，根据生产参数和生产数据计算出细纱捻度、牵伸倍数、轮班产量、累计产量、效率等指标并在终端显示。研究过程中，可以对细纱机当班生产数据(包括前罗拉速度、后罗拉速度、停机次数、停机时间、 车速、牵伸倍数、捻度、品种、号数、实际产量、开台效率等)进行浏览、查询以及统计分析。在此基础上，选择了如表1所示的细纱机运行参数。在成纱过程中，当实际监测的运行参数与设定的工艺参数之间数值不一致时，被认定为细纱机性能发生了退化。

表 1 细纱机运行状态参数

由于并非所有监测到的数据都能表征细纱机的性能变化，因此根据上述的序关系法与熵权法相结合的方法，计算表1中的15个参数的综合权重。选取综合权重大于0.5的参数，形成的监测参数综合权重变化，如图1所示。

图 1 细纱机性能参数筛选Fig.1 Screening of performance parameters of spinning frame

由图1可知，序号为4(锭子速度)、11(后罗拉转速)的参数权重大于0.5。因此，选取锭子的速度偏差和后罗拉转速偏差作为细纱机性能退化参数。

为了验证所选取参数能够较好的表征细纱机的性能退化，监测2个参数的变化对成纱质量的影响。邵景峰[21]在研究中验证，在整个纺纱过程中有5个指标(条干不匀、粗节、细节、断裂强度和断裂伸长)易受各类异常因素的影响，其中“断裂强度”最为显著。因此,监测锭子速度、后罗拉转速等2个参数的变化对“断裂强度”的影响,结果如图2所示。

图 2 断裂强度变化Fig.2 Variation of fracture strength

由图2可知，在2个指标的影响下断裂强度一直在降低，与实际过程中相对应。随着细纱机锭速的增加，纱线张力也会随着锭速的提高而相应的增加。如果锭速过高，会使纱线从罗拉到导纱钩处出现抖动，影响后罗拉的速度，导致罗拉缠花，使纱线断裂强度降低、纱线断头。实验结果表明，选择这2个参数作为细纱机的性能变化的参数是可行的。

3.2 算例验证

选取指标为锭子速度和后罗拉转速，对采集到的数据进行仿真，结果如图3所示。同时，得到两者之间的散点图，如图4所示。

图 3 数据偏差仿真结果Fig.3 Simulation results of data deviation

由图3和图4大致可以看出来，随着成纱过程的不断推移，锭子速度增加，后罗拉转速也在增加。为了进一步验证两者之间的相关关系，在实际纺纱过程中对其进一步实验。借助Copula函数的优点，分别选择Copula函数的4种不同形式进行细纱机性能退化过程的参数估计，同时进行AIC准则的检验，结果如表2所示。AIC值越小，说明函数拟合效果越好，同时可得到不同Copula函数对应的参数θ估计值。

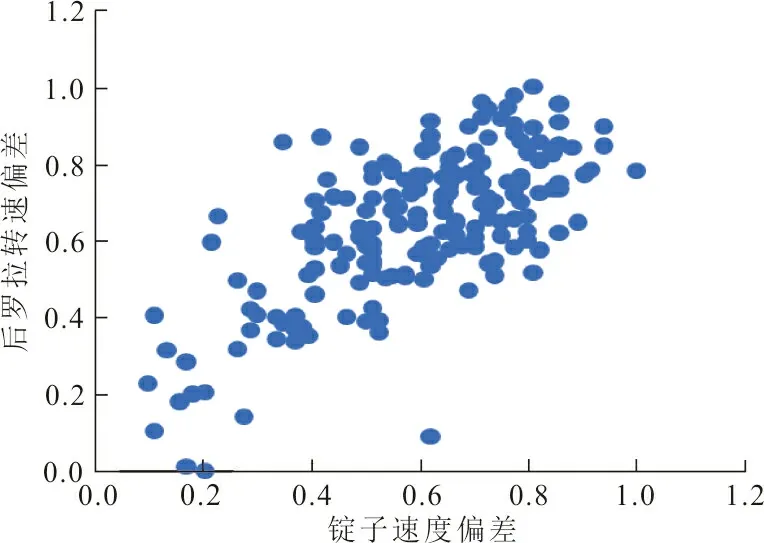
图 4 数据散点Fig.4 Scatter plot of data

表 2 Copula函数AIC值

从表2可以看出，Clayton Copula函数的AIC值最小，故选用此函数进行相关性建模。利用Clayton Copula函数仿真得到的概率密度函数和联合分布函数如图5、图6所示。由图5、6可知，2种退化过程之间具有一定的相关性。

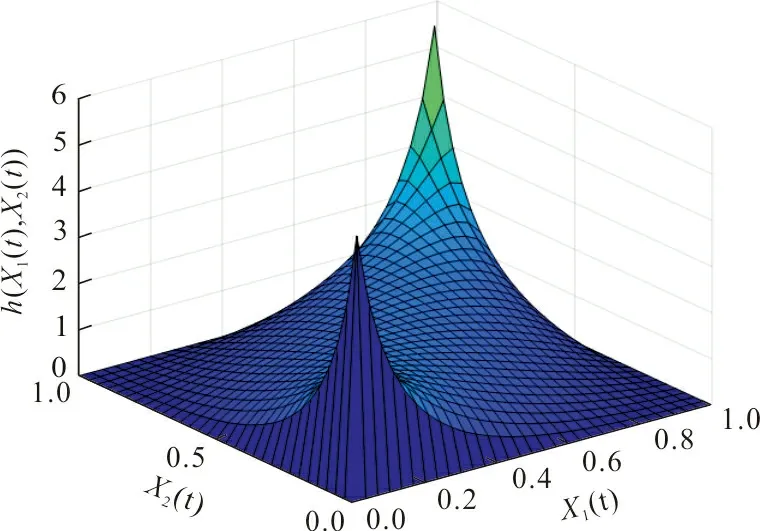
图 5 概率密度函数Fig.5 Probability density function

图 6 联合分布函数Fig.6 Joint distribution function

在此基础上，进一步利用相应的可靠性函数，对细纱机多元参数的可靠度进行仿真实验，得到如图7所示的多元参数相关可靠度曲线。

图 7 细纱机多元参数相关可靠度曲线Fig.7 Multivariate parameter correlation reliability curve

由图7可知，当监测时间小于10 d时，多元参数退化失效的可靠度趋近于1；当监测时间在10～20 d区间时，其可靠度迅速下降；当监测时间超过30 d时，其可靠度趋于零。这一结果说明：当监测时间在10～20 d区间时，多元参数退化失效的可靠度偏差大。企业在这期间应该进行维修。

4 结 语

针对细纱机的关键性能参数难以识别以及性能退化模型难以建立问题，分析细纱机性能特征，并筛选细纱机的监测参数，得到了关键性能参数。在此基础上，利用Copula函数探讨多种退化参数之间的相关性，利用Wiener随机过程描述了多元退化失效过程,较好地描述了细纱机的退化轨迹。利用最大似然估计以及贝叶斯理论的Gibbs算法估计参数，以此构建了面向细纱机多元性能退化过程的可靠性评估模型。依托细纱机的监测数据，进行了模型验证和对比分析，结果表明，构建的模型能够较好的表征细纱机可靠度变化。说明模型具有较高的准确性，有利于细纱机的可靠性评估，为细纱机的维修管理提供支持，进而提高纺纱质量。