基于网格化规划的城市配电网精准投资策略
2022-03-17邵建伟刘士齐潘兴亚陈嘉沁胡凡君王军华
潘 笑,邵建伟,刘士齐,潘兴亚,陈嘉沁,胡凡君,王军华
(1.武汉大学电气与自动化学院,湖北 武汉 430072;2.广东电网有限责任公司珠海供电局,广东 珠海 519031;3.云南电力科学研究院,云南 昆明 650217)
0 引言
城市配电网直接面向广大电力用户,肩负着连接用户和电源的使命[1-3]。对城市配电网进行科学合理的规划不仅可以提升供电可靠水平,而且可以减少配电网建设的投资成本。
为适应城市发展的需求,城市配电网投资规划的科学性与合理性尤为重要[4-6]。文献[7]综合考虑配电网的供电安全性、生态可持续性和经济竞争力,提出了一流配电网的规划建设思路。文献[8-9]则从不同的角度对城市配电网的发展路径进行综合评估与规划。因为城市配电网规划需要结合电网特点、城市发展需求等多方面因素,而且投资项目繁多,区域差异性较大,针对配电网的统一规划无法实现配电网的精准合理规划。2020 年12 月,为实现配电网的高质量发展,提高城市配电网投资的精准性与科学性,国家电网有限公司颁布了《配电网规划设计技术导则》[10],详细阐述了供电网格的划分要求,提出配电网规划应全面推行网格化规划方法。文献[11]将配电网双Q 规划方法应用在不同供电网格的投资规划中,对不同网格进行差异化求解,从而实现网格规划的有序性与经济性。文献[12]综合考虑网格规划的经济性与可靠性,对网格规划的投资成本及可靠性提升进行量化分析,建立网格投资规划的多目标模型,对各网格的规划发展具有参考意义。文献[7-9,11-12]主要针对配电网整体或单个供电网格的规划进行分析,没有考虑网格规划与配电网规划之间的互相影响,无法实现《导则》中“由下而上、上下结合”的发展要求。
本文基于“网格化规划”的概念,提出了一种基于网格化规划的由下而上的城市配电网投资优选模型,利用改进的第二代非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm Ⅱ,NSGA-Ⅱ)得到城市配电网的精准化投资方案,有效提高城市配电网投资的精准性,为城市配电网的个性化、精细化发展提供决策支撑。
1 城市配电网投资分析
1.1 城市配电网的网格化原则
随着电网建设的不断发展,用户对于电力服务的要求也越来越高。将配电网区域进行适当的网格化划分,可以有效提高配电网规划的精准性与有效性[13-14]。
依据《导则》中相关技术条款要求,结合城市电网特点,考虑供电指标要求、负荷发展趋势、负荷特性、变电站供电范围等因素,可以将供电区域划分为A+,A,B,C,D 类供电区域。
网格化规划应在供电区域划分的基础上,结合地区空间发展规划,充分考虑区域内负荷性质,以城市主干道路、河流、铁路等易于形成清晰供电范围的天然分界线为边界,对城市供电区域进行区域细化,得到若干个供电网格[15]。
1.2 城市配电网投资指标分析
城市配电网的投资发展因城市发展阶段及电网薄软环节的差异存在不同的投资侧重[16-20]。本文同时考虑电网公司、电力用户及社会发展的需求,将城市配电网的投资方向主要分为供电可靠性提升、网架结构优化以及运行效率提高3 方面,具体投资内容及关键指标如表1 所示。

表1 城市配电网投资内容及关键指标Table 1 Investment content and key indicators of urban distribution network
文献[21]通过主成分分析及灰色关联分析,证明了表1 中的7 个关键指标可以有效反映各类投资的效果,指标与各投资类别具有较强的关联性。因此可以通过配电网历史投资数据及关键指标数据,实现配电网投资与关键指标之间的量化分析。即:

基于1.1 节中的网格划分原则,将城市电网划分为N个供电网格,网格规划同样满足式(1)中的函数关系。为了得到网格关键指标与投资成本之间的基本函数关系,即求解各个网格的关系矩阵A,暂不考虑临近网格的投资组合以及电网公共设备的建设投资对目标网格可靠性的影响。
2 城市配电网精准投资模型
本文提出的城市配电网投资模型需要实现基于不同规划主体的双层优选。上层模型针对城市配电网规划的投资分配问题,结合各网格的电网现状,完成各网格投资金额的最优分配;下层模型针对网格的精准化投资问题,同时考虑可靠性与经济性的优化目标,完成网格规划内各投资类别的金额分配。在常规规划中,规划者容易忽略下层规划结果对上层的影响,本文则提出一种由下而上的精准化投资模型,如图1 所示。

图1 基于网格化规划的城市配电网精准化投资模型Fig.1 Accurate investment model of urban distribution network based on grid planning
2.1 网格投资的多目标规划模型
2.1.1 多目标函数
在进行网格规划时,需要同时考虑经济性和可靠性目标,其中可靠性目标由关键指标F3表示。以第n个供电网格规划为例进行分析,网格规划的经济性Y1与可靠性Y2目标分别为:
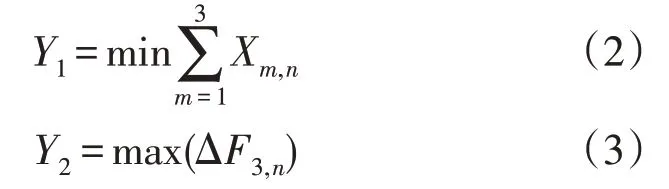
式中:Xm,n为第n个供电网格规划中对第m类投资的投资额;ΔF3,n为第n个供电网格在投资改造前后,用户年平均停电时间的变化值。
2.1.2 约束条件
供电网格的规划问题除了需要考虑投资额及可靠性的约束,还需要考虑关键指标的约束,即:
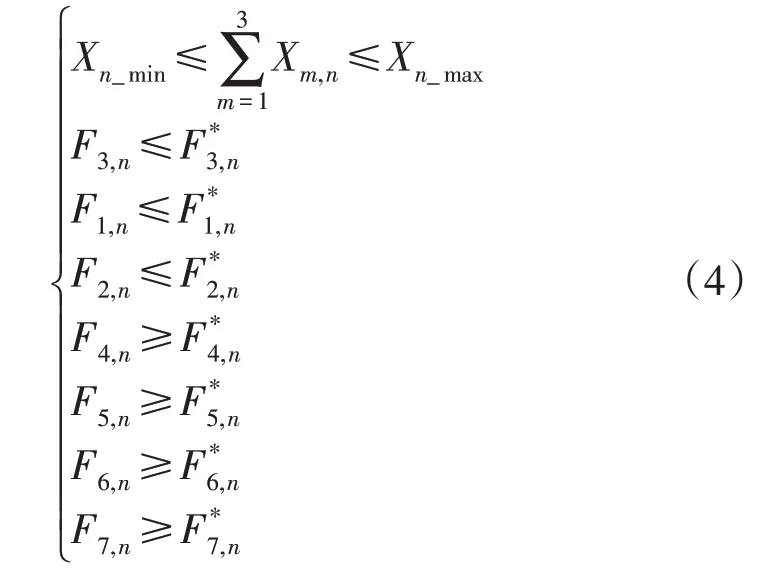
式中:Xn_max,Xn_min分别为本次网格规划的投资金额上下限;Fi,n为规划后的配电网关键指标,其中,i=1,2,…7;为用户年平均停电时间的期望值上限;分别为线路重过载条数占比与主变重过载台数占比的期望值上限;分别为线路、主变压器“N-1”通过率的期望值下限;分别为线路轻载条数占比与主变轻载台数占比的期望值下限。
2.2 城市配电网的最优投资分配模型
基于2.1 节多目标优化模型,求解所有供电网格的最优Pareto 投资曲线。对曲线进行多项式拟合,得到每个网格的最优投资曲线方程:

2.2.1 目标函数
在完成网格规划的基础上,配电网规划主要考虑其经济性目标。首先将各网格的总投资值相加即可得到配电网规划的规划成本,然后利用产电比法[12]计算各网格可靠性提升产生的经济效益,综合考虑规划成本及经济效益,得到配电网规划的目标函数为:

式中:Pn为第n个网格的平均负荷;ηn,λn分别为第n个网格的电价系数与产电比系数。
结合网格的最优投资曲线方程,可以得到新的可靠性目标方程,即:

2.2.2 约束条件
城市配电网的规划问题约束条件为:

式中:Xmax,Xmin分别为配电网规划的投资金额上下限;δn为第n个网格在改造后统计周期内的用户总数;δ为城市配电网在改造后统计周期内的用户总数,即;ΔF3_min为本次城市配电网规划对于用户年平均停电时间减少的期望值下限。
3 投资模型求解
因为配电网层的规划模型是基于网格层的优化结果得到的,所以需要将配电网层的规划结果(各网格的最优投资总金额)映射到各网格的Pareto曲线上,才可以得到各网格的最优投资组合。但是基于传统NSGA-Ⅱ算法优化得到的Pareto 曲线中的各离散点分布均匀程度较差,导致映射过程中可能会存在较大误差。为了提高各网格最优投资组合的精准性,对传统的NSGA-Ⅱ算法进行改进以提高Pareto 曲线中解的均匀程度。
3.1 改进的NSGA-Ⅱ算法
传统的NSGA-Ⅱ算法采用二进制锦标赛实现优秀个体的选择,容易使最优解陷入局部最优,拥挤度距离也无法全面地衡量个体的空间分布,无法保证最优解的均匀分布[22]。本文提出一种新的种群优选策略,基于动态的个体淘汰方案可以有效增加最优解的多样性,将个体的拥挤度距离与基于支配关系的上层距离相结合,综合考虑个体的空间分布,有效改善最优解的均匀程度。
3.1.1 动态的个体淘汰方案
为了提高种群的多样性,提出一种动态的个体淘汰方案,综合考虑非支配排序以及迭代次数的影响,确定每一次迭代过程中各层的淘汰个体数目,具体的淘汰方案如下:

式中:dg为第g层被淘汰个体的数目;lg为淘汰前第g层个体的数目;pg为第g层被淘汰个体占原先个体的比例;[]表示取整;G为总层数,其中g=(1,2,…,G);xt为迭代次数影响因子;t为本次迭代次数;tmax为最大迭代次数;α,β,μ为比例因子,其中α的值使个体淘汰方案满足式(12)的约束,β的值则影响各层次的pg随t的变化趋势,本文赋值为2;μ的值决定t对pg的影响程度,本文赋值为0.2。

式中:H为初始种群的个体数量。
3.1.2 考虑上层个体的拥挤度计算
个体淘汰方案可以实现个体的逐层优选,但是在对某一层个体进行优选时,需要考虑个体的空间分布。传统的拥挤度距离只考虑了本层个体的分布情况,计算公式为:
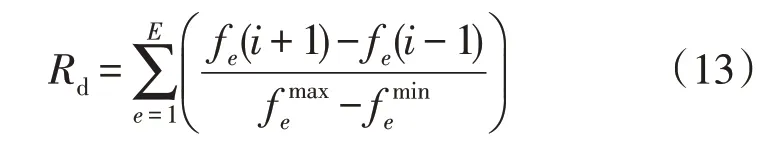
式中:Rd为个体i的拥挤度距离;E为优化目标的个数;fe(i+1),fe(i-1)分别为个体i在同层的两个相邻个体在目标e的函数值;分别为所有个体在目标e的函数值的极值。
基于个体之间的支配关系,将个体与上一层的优选个体的最小距离定义为上层距离,具体表达式为:

式中:Rf为个体i的上层距离;fe(i)为个体i在目标e的函数值;if为上一层中可支配个体i的个数;fe(if)为其在被支配个体在目标e的函数值。
综合考虑个体在本层的拥挤度距离以及和其支配个体的上层距离,得到考虑上层个体的拥挤度距离计算结果Rs,表达式为:

将每一层两端个体的Rd设为无穷大。若某个体不属于其上层所有个体的支配集,则将其Rf取为该个体所在层的所有个体的Rf最大值。第一层个体的Rf则均设为0。需要注意的是当淘汰一个个体时,其相邻个体的Rd会随之改变,所有个体的Rf均保持不变,因此在每一个个体淘汰后,需要对其相邻个体的Rd重新计算。
3.1.3 算法流程
基于动态个体淘汰方案及拥挤度的计算策略,改进的算法流程见图2。
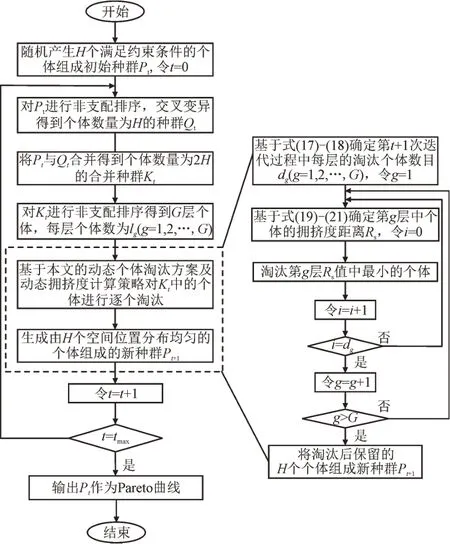
图2 改进的NSGA-Ⅱ算法流程图Fig.2 Flow chart of improved NSGA-Ⅱalgorithm
3.1.4 评价指标
为了对本文提出的改进算法的效果进行对比分析,引入空间评价方法[22]对解集的均匀性指标Δ(无量纲)进行评价,Δ 的数值越小,说明解集的均匀性就越好,评价函数为:
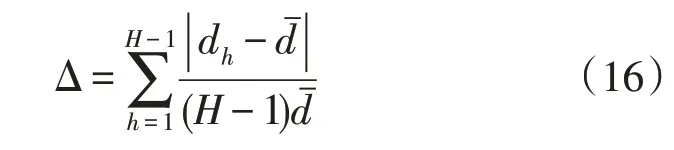
式中:dh为非支配解中两个连续向量的标准欧氏距离[23](无量纲);为所有dh的平均值。
3.2 模型求解方法及流程
基于改进的NSGA-Ⅱ算法多目标模型进行求解,其求解结果可以作为网格当前的最优投资曲线,所有网格的最优投资曲线共同决定了配电网模型的目标函数;然后利用遗传算法[24]对2.2 节中的单目标模型进行求解,其求解结果即为各网格的最优投资总金额。求解流程图如图3 所示。

图3 城市配电网精准化投资的求解流程图Fig.3 Flow chart of solving accurate investment model of urban distribution network
4 算例分析
以某城市X 区电网改造为例进行分析,X 区所辖供电面积316.9 km2,用户年平均停电时间为1.75 h,用户数为65.91 万户,供电区划分为A+、A、B 类供电区域,按照网格划分原则,分为以下16 个网格,各网格的信息如表2 所示。

表2 X区电网的各网格信息Table 2 Grid information of X area power grid
4.1 供电网格的最优投资分析
为了实现对X 区电网的精准化投资,需要对16个供电网格进行差异化分析。首先求解网格规划优选模型,然后拟合得到供电网格的最优投资曲线。以网格1 为例进行具体分析。
4.1.1 算法性能验证
为了验证改进算法的效果,将网格1 的优化模型同时代入到传统的NSGA-Ⅱ算法及本文改进的NSGA-Ⅱ算法中。将种群数量设为100,通过改变迭代次数,计算两种算法的解集均匀性指标Δ,对比结果如图4 所示。
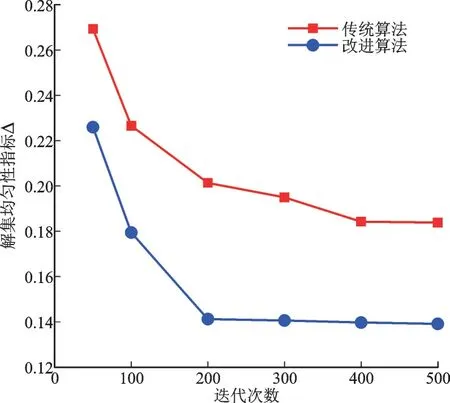
图4 两种算法的解集均匀性指标Δ比较Fig.4 Comparison of solution set uniformity index Δwith two algorithms
由图4 可知,随着迭代次数的增加,Δ的值逐渐变小,说明解集具有更好的均匀性。在相同的迭代次数时,改进NSGA-Ⅱ算法得到的解集具有更好的均匀性指标,说明本文提出的算法能有效改善Pareto 最优解的分布情况,提高优化过程的多样性。从均匀性指标的变化趋势可以看出传统的NSGA-Ⅱ算法在迭代400 次时具有较好的收敛效果,而本文提出的算法在迭代200 次时已经具有较好的收敛效果,说明改进NSGA-Ⅱ算法具有较好的收敛性。
将迭代次数设为500,通过改变种群规模,对两种算法的解集均匀性指标进行计算,对比结果如表3 所示,图5 为种群规模设为100 时的Pareto 曲线对比图。

表3 两种算法的解集均匀性指标比较Table 3 Comparison of solution set uniformity index with two algorithms
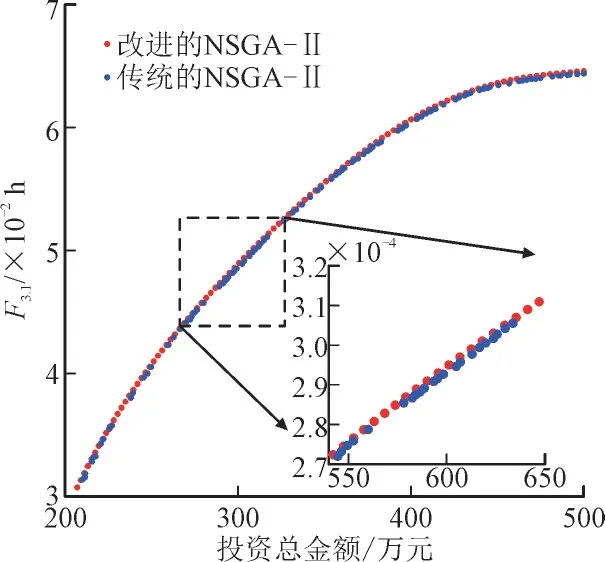
图5 网格1规划的Pareto最优解曲线Fig.5 Pareto optimal solution curves of planning for grid 1
由表3 和图5 可知,本文提出的算法能有效改善Pareto 最优解的分布情况,增加了优化过程的多样性,具有较快的收敛速度。
4.1.2 优化结果分析
对网格1 规划得到的Pareto 最优解曲线进行多项式拟合,可以得到如式(17)的规划最优投资曲线方程。为了提高多项式拟合的精度,网格投资金额的单位设为千万元。
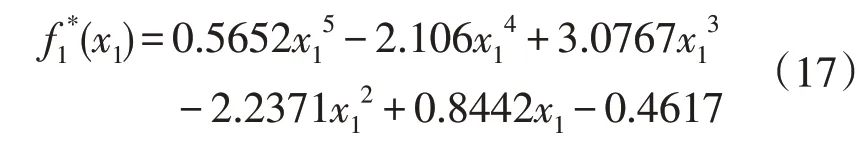
式中:x1为网格1 的投资总金额,单位为千万元,f1*(x1)为网格1 的用户年平均停电时间降低的最优值。
依次对所有网格的最优投资曲线进行求解,可以发现各网格的最优投资曲线均呈现如图5 所示的变化规律,即在满足规划目标的基础上,可靠性的改善程度随着投资的增加而逐渐变慢。然而,各网格最优投资曲线的变化范围及变化程度存在一定的差异性,因此在城市配电网规划中,将各网格的最优投资曲线代入到总体投资分配的优化模型中,可以在满足各网格差异化投资需求的基础上,提高城市配电网投资的精准性。
4.2 基于最优投资曲线的城市配电网投资分配
对X 区电网规划的投资金额进行最优分配,需要结合16 个供电网格的最优投资曲线。将每个网格的投资总金额作为优化变量,结合各个网格的最优投资函数曲线,获得配电网优化模型中的目标函数。基于城市配电网的规划要求,X 区电网的用户年平均停电时间需要低于1.65 h,投资总金额不能超过6 000 万元,各个网格的用户年平均停电时间的期望值分别为0.55 h,0.58 h,0.67 h,0.80 h,1.95 h,2.08 h,2.15 h,2.10 h,1.98 h,2.14 h,2.05 h,1.90 h,2.05 h,2.80 h,3.05 h 和2.98 h。将目标函数及约束条件代入改进遗传算法中,种群数量设为100,迭代次数设为500,得到的优化结果如图6 所示。

图6 城市配电网投资分配的优化结果Fig.6 Optimization results of investment allocation in urban distribution network
由图6 可知,属于同一供电分区的各网格最优投资结果较为相近,而且最优投资结果的分布具有一定的规律,即可靠性提升效果与投资额之间呈现一定的正相关关系。然而,属于不同的供电分区的网格的投资敏感性则具有较大差异,相比之下,A+、A、B 类供电区域的投资敏感性逐渐增大。
4.3 规划结果分析
结合各网格的Pareto 最优解曲线,求解各网格的精准化投资,映射得到的最优投资方案见表4。
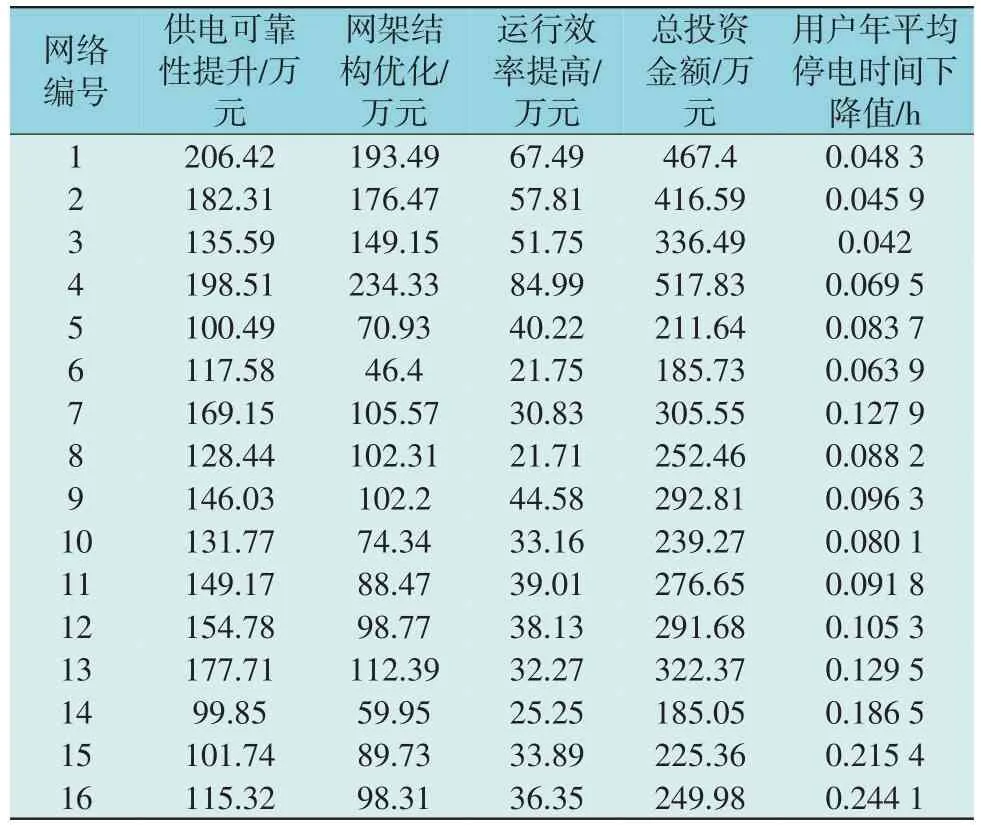
表4 各个供电网格的最优投资方案Table 4 Optimal investment plan for each power supply grid
为了验证本文提出的规划模型的有效性,作为对比,在不考虑网格化影响的情况下,对目标城市配电网进行总体规划,通过传统的单目标与多目标算法对配电网的总体投资规划进行求解。在传统的单目标求解中,将经济性目标及约束代入遗传算法中进行寻优,得到的投资方案记为传统投资方案1;在传统的多目标求解中,同时考虑经济性与可靠性,代入NSGA-Ⅱ算法中进行寻优,利用基于模糊隶属度函数的满意度评价模型[25]对Pareto 解集中的所有非劣解进行评价,得到最优折衷解记为传统投资方案2。对比结果见表5。
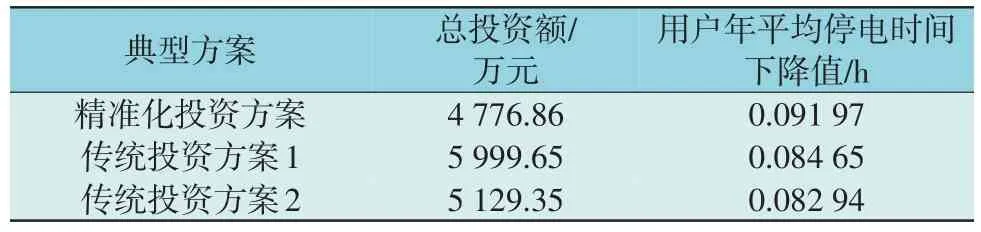
表5 规划方案对比Table 5 Comparison of planning schemes
由表5 可知,和传统的总体规划模型相比,本文提出的基于网格化规划的城市配电网投资模型不仅可以实现配电网的精准化投资,而且规划结果具有更好的经济效益和可靠性水平,满足各个供电网格的规划要求,提高配电网建设与城市发展的契合水平。
5 结论
结合城市配电网的精准化投资需求以及网格划分的实际情况,提出了一种基于网格化规划的自下而上的城市配电网最优投资模型。通过算例分析验证了本文所提模型的有效性。
1)结合各个网格的发展现状以及规划需求,对各网格的最优投资曲线进行求解分析。总体来说,在满足规划目标的基础上,可靠性的改善程度随着投资的增加而逐渐变慢。不同网格的最优投资曲线之间存在总体规律以及差异性,对于网格规划的目标设定以及方案选择具有一定的指导意义。
2)基于网格化规划的配电网投资优选方案不仅可以满足网格电网发展的差异化需求,而且可以实现针对城市配电网可靠性提升的精准化投资,具有较好的经济性。
3)对某一供电网格的投资-关键指标关系进行分析时,需要考虑临近网格的投资组合以及电网公共设备的建设投资对网格可靠性的影响。如何量化网格规划之外的影响因素对目标网格的影响,得到精准的“由下到上,上下结合”的城市配电网规划模型,将是本文未来研究的方向。
