基于Nakagami成像纹理特征检测微波热消融凝固区的方法研究

2022-03-16周著黄吴水才

医疗卫生装备 2022年2期

王赫，周著黄，吴水才

（北京工业大学环境与生命学部，北京 100124）

0 引言

肝细胞癌（hepatocellular carcinoma，HCC）是最常见的原发性肝脏恶性肿瘤，是癌症死亡的主要原因之一[1]。微波热消融术作为20世纪90年代的一种新兴技术，目前已成为治疗肝肿瘤的一种重要手段。微波热消融是一种使用频率≥900 MHz的设备诱导肿瘤死亡的电磁方法，其原理是通过水分子剧烈运动产生的热量造成肿瘤不可逆的凝固性坏死[2]。微波热消融术的理想状态是使坏死的凝固区范围完全覆盖肿瘤并形成5~10 mm的安全边界，从而达到“适形消融”，这样既可避免消融不足导致的肿瘤复发，又可防止过度消融对器官造成损害。因此，消融过程中的凝固区监测是国内外学者的研究重点。

为了弥补传统B超成像在监测过程中的不足，定量超声通过分析背散射回波射频信号来检测消融凝固区，其中包括散射子浓度、间距及直径等信息。目前，应用在肝肿瘤消融领域的定量超声主要有Nakagami统计分布模型法、零差K分布模型法、超声衰减系数法、散射子平均间距法、回波信号去相关法等[3]。Nakagami统计分布模型法应用比较广泛，该方法通过定量映射构建Nakagami参数分布图描述散射介质中超声散射子排列和浓度。由于消融过程中消融区的气泡作为强散射子导致该处散射子浓度增加，通过Nakagami参数可定量描述凝固区变化情况[4-6]。

图像纹理特征是一种人类视觉认知的关键组成部分，近年来常被应用于计算机视觉系统中，灰度共生矩阵（gray-level co-occurrence matrix，GLCM）是其中的代表性方法之一[7]，常用于肝脏、乳腺肿瘤、脑肿瘤的医学影像分析[7-10]，但目前还未见将GLCM应用于肝肿瘤微波热消融定量超声图像分析的报道。支持向量机（support vector machine，SVM）是由Vapnik[11]提出的数据分类方法，通过训练数据生成SVM模型并基于该模型实现分类。

本文提出一种基于GLCM和SVM的微波热消融Nakagami参数图检测凝固区的新方法。通过采集Nakagami参数图中凝固区与正常组织部分的图像获取SVM训练样本，并基于训练样本获取SVM凝固区识别模型；对整幅Nakagami参数图逐点滑动识别得到等大小的二值识别结果图；基于识别结果图使用多项式拟合（polynomial approximation，PAX）技术得到凝固区最终识别结果。

1 原理与方法

1.1 实验仪器与数据采集

1.1.1 实验仪器

本实验采用离体猪肝进行微波热消融实验。实验装置平台如图1所示，主要实验仪器设备包括南京康友公司生产的KY-2000微波消融仪、美国Terason公司生产的T3000型超声仪（用于采集超声射频回波信号）。

图1 实验装置平台

1.1.2 数据采集

用80 W微波热消融功率对离体猪肝进行60 s的消融实验，通过超声仪实时成像并以2帧/s的速度采集超声背散射信号（数据采样点为1 558，扫描线为256），共采集20组数据，获取其超声背散射信号，并沿消融针方向切开离体猪肝，测得其凝固区大小作为金标准。

1.2 Nakagami统计模型和成像

1.2.1 Nakagami统计模型

Nakagami统计模型是一种描述超声背向散射包络统计的通用模型[12]。在微波热消融过程中，组织由于受热产生气泡并发生微小的结构变化，在声学模型中可将这种变化视为超声散射介质中的散射子浓度或排列发生变化。在Nakagami统计模型中，超声背散射包络振幅r的概率密度函数公式为

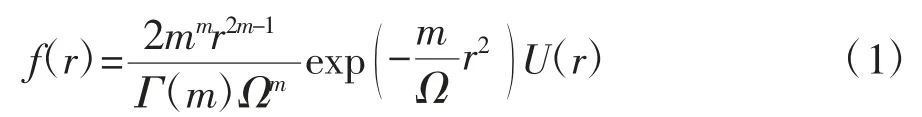
式中，Γ（·）表示伽马函数；U（·）表示单位阶跃函数；Ω表示尺度参数；m表示Nakagami参数。

假定E（·）表示统计均值，则可由公式（2）、（3）计算尺度参数Ω和Nakagami参数m：

式中，R为超声背向散射包络。

不同的m参数可定量表征由组织中散射体变化造成的不同包络统计分布。当01时，包络统计分布服从后瑞利分布[4]。

1.2.2 Nakagami成像

Nakagami成像是基于Nakagami参数m映射的一种定量超声图像。通过滑动窗口采集包络成像中的局部背散射包络信号并估计局部m参数值，将其作为新像素赋值给当前窗口；将上述滑动窗口以特定的窗口重叠率遍历整幅包络成像可获得m参数矩阵。滑动窗口的宽度将同时影响Nakagami成像分辨力和m参数估算准确度，为了更好地均衡二者关系，将窗口宽度设定为换能器脉冲长度的3倍[13]。图2为离体猪肝微波热消融B模式超声成像、Nakagami成像和病理大体图，其中图2（a）为B模式超声成像图，将m参数矩阵加以颜色映射并成像可得到Nakagami成像，如图2（b）所示。本研究选用的图像纹理特征GLCM要求计算图像为灰度图像，因此将m参数矩阵进行256灰度级数映射可得到如图2（c）所示的Nakagami灰度成像。微波热消融实验可得到消融针坐标及凝固区长短轴大小，根据该长短轴计算椭圆偏心率并以消融针坐标为中心勾画凝固区范围。图2（d）为离体猪肝剖面大体病理图（视为参考标准），以离体猪肝最大剖面的测量结果为金标准，检验本文提出的算法的准确度。

图2 离体猪肝微波热消融B模式超声成像、Nakagami成像和病理大体图

1.3 GLCM样本采集及特征提取

1.3.1 GLCM样本采集

Nakagami成像既包括凝固区范围又包括正常组织部分，因此需要采集不同部分的样本用于计算GLCM特征。本研究以像素大小为33×33的感兴趣区域在每一幅Nakagami成像中分别采集4例凝固区图像样本和4例正常组织图像样本，凝固区样本采集以靠近消融针位置处为宜。最终共在20例微波热消融数据中采集样本160例，其中凝固区图像样本80例，正常组织图像样本80例。图3为样本采集示意图。

1.3.2 特征提取

GLCM是一种提取灰度图像二阶统计量的方法，其表现形式是一个以图像灰度阶数Ng为边长的正方形矩阵。矩阵的元素p（i，j）为特定距离d和角度θ下的二阶统计量概率值[14-15]。简单地说，假定图像分别有Nx行和Ny列，且灰度阶数为Ng，那么图像矩阵的行列可表示为Lx={1，2，…，Nx}及Ly={1，2，…，Ny}，图像的灰度范围可表示为Gx={0，1，…，Ng-1}。将灰度级数分配至每个Lx×Ly范围内的像素点，由相对频率矩阵C（i，j）表示图像的纹理特征关系。C（i，j）为在特定的（d，θ）窗口中灰度级别i和j出现的次数，概率密度可表示为

GLCM矩阵元素p（i，j）定义如下：

本实验基于GLCM矩阵计算得到4个特征值：能量（Energy）、对比度（Contrast）、同质性（Homogeneity）、相关性（Correlation）。上述特征值的计算公式分别如（6）~（9）所示：

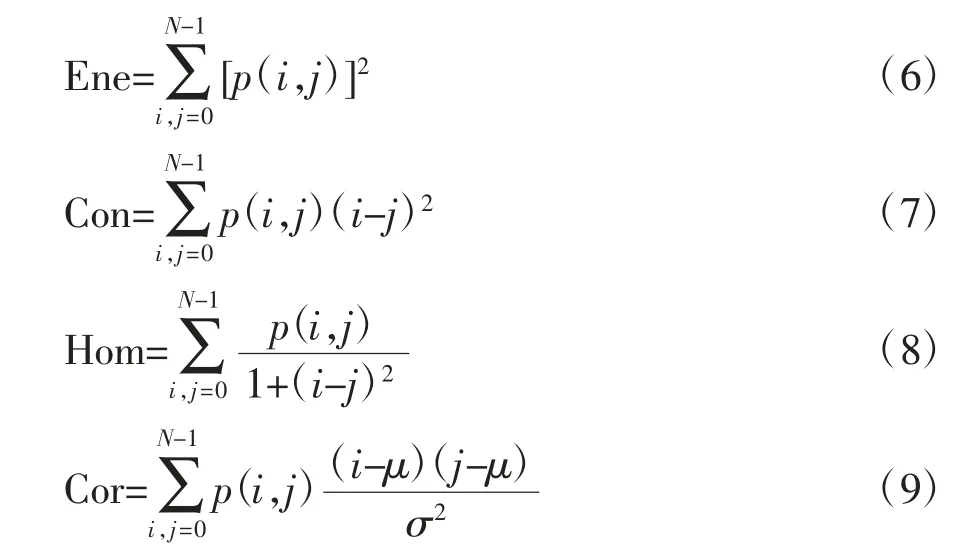
式中，μ、σ分别为均值和标准差。

能量是一种度量图像灰度均匀性的特征，均匀的图像通常仅由几个灰度阶数构成，因此图像越均匀其能量值越大；对比度反映了图像中的局部灰度阶数变化，若图像中存在大量的灰度变化，则其具有高对比度值；同质性是图像中不同于能量的另一种灰度均匀性的度量特征值，图像灰度越均匀，对应的同质性越大；相关性用于度量相邻像素或特定位置像素之间灰度的线性相关性，它反映了灰度图像的局部灰度依赖性，若灰度值沿某一方向延伸越长，则其相关性越大[14]。

GLCM的大小为灰度图像的灰度阶数Ng的二次方，过大的Ng会带来大量的计算量进而影响计算效率。为方便GLCM计算，将输入图像的Ng缩放至16位。设定步长d为1，方向（角度）θ为0°、45°、90°、135°。对上述4个特征值分别以设定的d和θ计算特征值，并以不同方向上的同一特征值的均值作为最终结果。

1.4 SVM模型训练

SVM是一种基于统计学习理论的机器学习方法，也是广泛应用于模式识别领域的常用工具。利用SVM可以通过不同的核函数组合多个自变量实现对因变量的估计。假定D为训练样本集合，则有D={（X1，Y2），（X2，Y2），…，（Xn，Yn）}，其中第i个特征量Xi∈Rn，标签Yi∈{0，1}。SVM的实质是建立一个具有最大间隔的划分超平面，实现对训练样本的划分，也就是对公式（10）的求解：

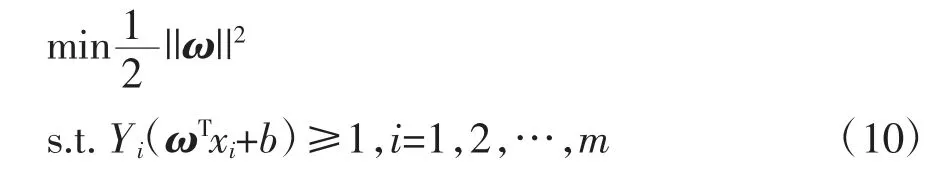
式中，ω为决定超平面方向的法向量；b为位移项，决定超平面与原点的距离。由于并非所有样本都可以在二维空间被线性可分，因此需要引用核函数将样本映射到更高的维度，从而寻找超平面进行划分。常用的几种核函数为线性核、多项式核、径向基函数（radial basis function，RBF）核、拉普拉斯核、Sigmoid核。为了避免模型分类时出现过拟合或欠拟合，需要确定最优惩罚参数c及核函数参数g。

本文选用LIBSVM工具箱进行SVM模型训练[16]，确定核函数为RBF核。选用十折交叉验证法选择最优参数c和g，最终确定c和g分别为2.639和0.5。

1.5 凝固区识别

在获取SVM模型后，对Nakagami参数图以33×33大小的像素矩阵进行逐点滑动识别。具体而言，首先对Nakagami参数图以0进行边界填充，将填充后的图像以33×33大小的像素块进行逐点块分割处理。原始Nakagami参数图大小为360×360，边界填充并块处理后共分割为129 600个子图像块。对每一个图像块分别进行GLCM特征提取并进行归一化，由SVM进行分类处理，凝固区标签为1，正常组织标签为0，最终重建可得到凝固区识别图（二值图像）。对凝固区识别图进行删除小面积分量和孔洞填充2种形态学图像处理，并结合PAX获取最终凝固区识别结果[17-18]。图4为本文算法的流程图。

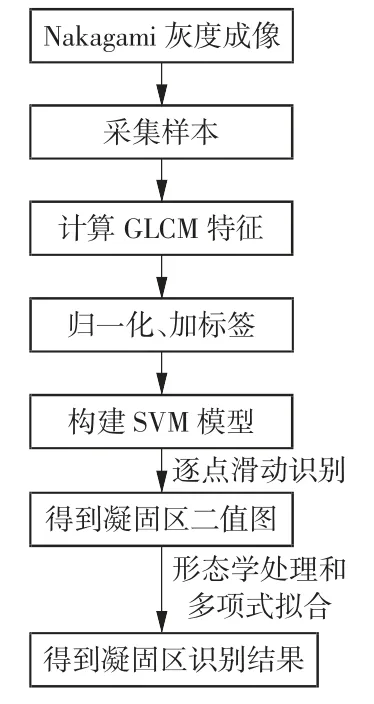
图4 本文算法流程图

2 实验结果

2.1 GLCM特征对比

箱线图能够直观反映数据的分布关系，GLCM特征值箱线图如图5所示。皮尔森相关系数是一种描述2个变量之间线性关系强弱的统计量，2个变量的皮尔森相关系数的绝对值越接近0，则表明二者线性相关性越弱；越接近1，表明二者线性相关性越强[18]。分别计算上述4个GLCM特征值中凝固区样本和正常组织样本的皮尔森相关系数，结果显示能量、对比度、同质性、相关性4种GLCM参数的皮尔森相关系数的绝对值分别为0.104 7、0.091 8、0.048 6和0.109 3，4种GLCM特征值的样本间皮尔森相关系数都接近0。结果表明，凝固区样本与正常组织样本的4种GLCM特征线性无关，可以作为训练样本进行SVM模型训练。

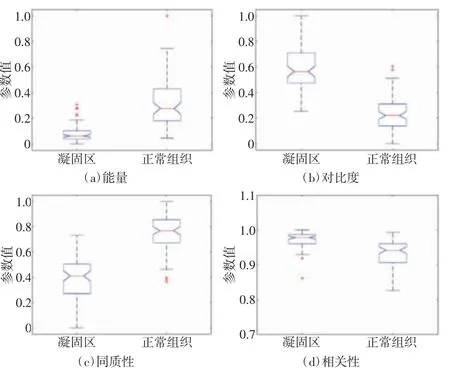
图5 GLCM特征值箱线图

2.2 SVM训练结果

使用分类准确率（accuracy，ACC）、平均平方误差（mean squared error，MSE）、相关系数r2作为衡量SVM识别能力的量化指标。公式（11）~（13）列出了上述3种指标的计算方法：

式中，TP为真正例；TN为真负例；FP为假正例；FN为假负例。将160例样本数据按3∶1随机划分为120例用作训练集，40例用作验证集。实验结果显示，训练后的SVM模型在验证集上的ACC为90%，MSE为0.1，r2为0.646 5。

2.3 凝固区识别结果

凝固区识别结果如图6所示。图6（a）为SVM凝固区识别模型初步识别结果，可以看到图像下方有一些多余的识别结果。这些多余识别结果可能是图像中存在一些高亮度区域噪声，因而被SVM模型错误识别为凝固区。经过图像形态学处理（孔洞填充、小面积分量删除）后得到图6（b）。经过实验测试得到，当PAX的参数为4阶、-6 dB等高线时候拟合效果最佳。图6（c）为PAX成像，图6（d）为PAX成像叠加在原始Nakagami成像后的结果图。

图6 凝固区识别结果图

2.4 凝固区面积检测准确度

通常凝固区可近似看作椭圆形，因此利用公式（14）可计算凝固区面积S，根据公式（15）可得到PAX成像识别凝固区准确度。

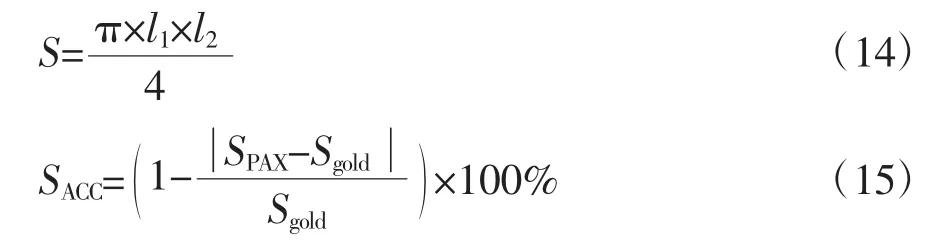
式中，SACC为凝固区面积检测准确度；SPAX为PAX成像计算面积；Sgold为猪肝消融后测量得到的面积（金标准）。本实验总计验证20例猪肝组织微波热消融数据。传统Nakagami方式在得到Nakagami参数成像后直接进行PAX得到近似椭圆形凝固区，也可通过公式（14）进行面积计算。结果显示，经过SVM模型识别后的凝固区与传统Nakagami成像准确度分别为（87.75±7.74）%和（84.38±13.52）%。

Bland-Altman是在分析化学及生物医学中常见的相关性统计法[19-20]。20例数据经SVM模型识别后的凝固区面积SSVM与金标准的Bland-Altman回归分析图如图7所示。从图中可以看出，20例数据中有18例（90%）处于95%一致性界限区间内，95%的一致性界限区间的计算方法为Mean±1.96Std（Mean和Std分别为平均值和标准差）。结果表明，本实验提出的SVM模型识别的凝固区面积与金标准具有很高的一致性。

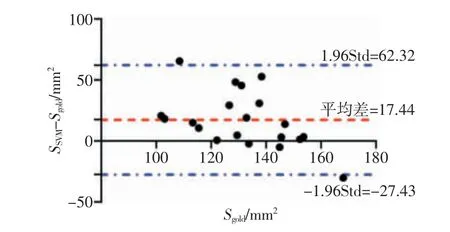
图7 Bland-Altman回归分析图

3 讨论

微波热消融凭借其微创性、易恢复、可操作性强等优势在肝肿瘤治疗领域的地位不断提高，但消融过程中的凝固区检测一直是亟须解决的问题。超声作为常见的医学成像技术被广泛应用于微波热消融术中。常见的超声监测方法包括超声弹性成像[21-22]和定量超声成像[4，17，23-26]。

目前，Nakagami参数成像作为定量超声监测肿瘤微波热消融热凝固区变化的常用方法之一，已被证实可有效监测凝固区面积。Zhang等[25-26]使用Nakagami参数成像监测高强度聚焦超声消融和微波热消融，对Nakagami参数变化加以颜色映射，并将m参数发生显著变化的区域视为凝固区。Zhou等[4]对Nakagami参数成像图应用PAX勾画出等高线，从而确定凝固区范围。本文通过提取Nakagami参数图像的纹理特征对凝固区进行识别，图像纹理特征可表述肉眼无法观察到的图像局部高阶信息从而对图像进行识别分割[27]。传统的Nakagami参数成像仅利用m参数的大小变化单一地判断凝固区范围，本文提出的方法通过分析更深层的灰度阶数变化关系来判断凝固区范围。这种灰度阶数的变化通过计算特定距离、角度的像素对的概率统计对选定区域内的纹理特征进行定量描述，有效弥补了传统方法简单依靠m参数数值大小关系判定凝固区的不足。

本文选择能量、同质性、相关性、对比度共4个GLCM特征参数。能量和同质性反映了图像灰度阶数的均匀程度。由于正常肝脏组织的肝细胞直径为20~30μm，因此可被视为回波散射性低的弱散射子；而凝固区由于肝脏细胞发生微小结构变化并且上方出现气泡，因此可被视为回波散射性高的强散射子。上述关系在Nakagami-m参数上表现为m参数在正常组织处变化相较于凝固区处更微小，且这一特性在计算GLCM时的技术压缩后更明显。因此，正常组织样本的能量及同质性大于凝固区，在图像上反映出的纹理特征更加均匀。对比度反映了图像的明暗变化关系。由于热消融过程中的温度以消融针为中心向外逐渐减弱，因此对组织的损伤程度也逐步减弱，在Nakagami-m参数中表现为m值由凝固区边界至消融中心逐步增大，因此凝固区内的灰度阶数变化相较于正常组织更大，在图像纹理特征中表现出的明暗关系更复杂。同理，由于m参数由外向内逐渐增大，在图像纹理特征上表现为灰度值沿某一方向延伸，因此凝固区相关性高于正常组织部分。

将本文提出的方法与传统Nakagami参数成像进行对比可以看出，凝固区在传统Nakagami参数成像上表现为高亮度区域但边界并不明确，而基于图像纹理特征的SVM识别模型可以识别出完整轮廓，结合PAX可更精准地拟合出凝固区边界。通过对20例离体猪肝微波热消融数据进行验证后发现，本文所提的方法准确度较原始方法提高约3.37%。经过Bland-Altman回归分析后发现，基于图像纹理特征的识别结果与金标准高度一致。

本文的研究在未来应在以下几个方向进行改进。首先，通过改变不同的微波功率及消融时间，增加样本数量并使样本更加多元；其次，Nakagami成像本身存在的一些噪声会影响SVM模型识别准确度，因此需探究一种噪声抑制方法改进Nakagami成像；最后，可尝试通过融合不同定量超声图像的GLCM特征值及定量参数训练SVM识别模型，提高凝固区的识别准确度。