基于代价函数的电动飞机脚蹬系统可靠性分配
2022-03-16丁一宁雷洞婷杨金洋赵为平周国庆
王 锋,丁一宁,雷洞婷,杨金洋,赵为平,周国庆
(1.辽宁通用航空研究院 直升机研发室,沈阳 110136;2.沈阳航空航天大学 a.航空宇航学院,b.机电工程学院,沈阳 110136)
近年来,新能源产业在人们生产生活中扮演的角色越来越重要[1],其中,电动航空也成为近期航空业最重大的技术创新之一。电动飞机因其产业优势科技含量高,具有广阔的市场应用前景,在国内外受到高度重视[2]。
20世纪80年代,我国开始进行民用飞机可靠性的研究工作,刘建军[3]、张琳等[4]对我国民用飞机及发动机可靠性工作进行分析。刘飞等[5]、刘潮东等[6]则提出基于成本考虑的系统可靠性指标分配方法。商兴华等[7]针对目前现有的中国通航运输飞机飞行可靠性资源分配管理方法当中存在的一些问题,提出一种新的飞机可靠性资源分配方法。石鹏[8]对非航电系统的可靠性分配方法进行了研究,并进行可靠性分配计算。李玉峰[9]采用GO法与状态概率矩阵算法相结合的运算方法对电动飞机电推进系统可靠性建模,运用Matlab语言进行系统的仿真研究,验证了该方法在提高计算效率与精度方面的优点。李峰等[10]、王浩等[11]利用遗传算法系统可靠性分配优化模型。徐立新[12]针对民用航空发动机空中停车的问题,制订了一套可靠性分析、监控、维修和管理的实施框架。
本文针对某型电动飞机脚蹬控制系统设计中的可靠性问题,通过建立相关可靠性模型,参考广义成本函数[13]并结合脚蹬系统实际情况,引入脚蹬部件重要度和系统实际成本的归一化参数,重新构建了能够较好地描述系统成本特性的成本函数,结合遗传算法对脚蹬控制系统可靠性分配进行优化,最终对可靠性结果进行分析。
1 脚蹬系统结构和可靠性框图
电动飞机操纵系统采用推拉钢索结构设计。操纵控制系统主要用于控制飞机飞行轨迹和姿态,由具有升降机主舵、副翼和飞机方向舵的3个操纵控制机构组成。本文的研究对象是电动飞机的脚蹬操纵系统,其由脚蹬、扭力管、前轮推拉杆、前轮转弯摇臂、方向舵推拉钢索、方向躲摇臂等零部件组成。飞行员踏脚蹬,脚蹬带动方向舵推拉钢索对方向舵进行操纵,从而实现对飞机航向的控制。飞机着陆时飞行员通过踏脚蹬作用于前轮操纵杆对前轮进行操纵,实现飞机地面的转弯,具体结构如图1所示。
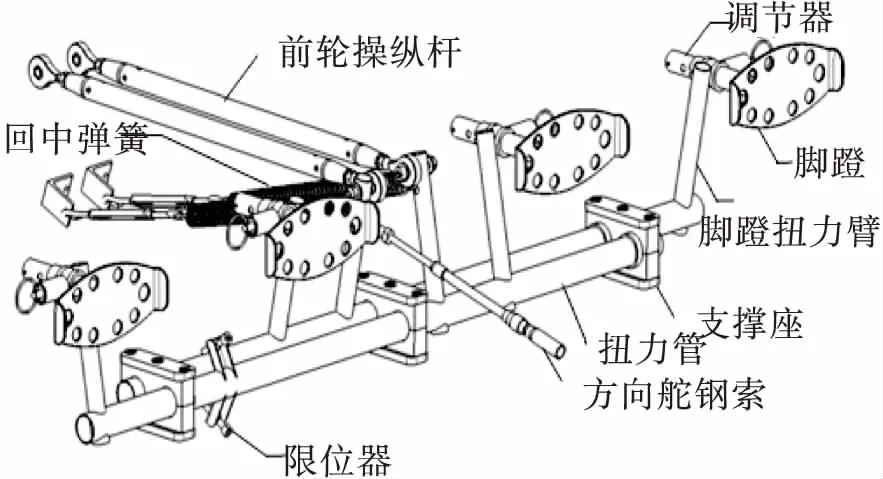
图1 脚蹬系统结构图
整理脚蹬系统的组成和结构关系,得到系统的可靠性框图如图2所示。
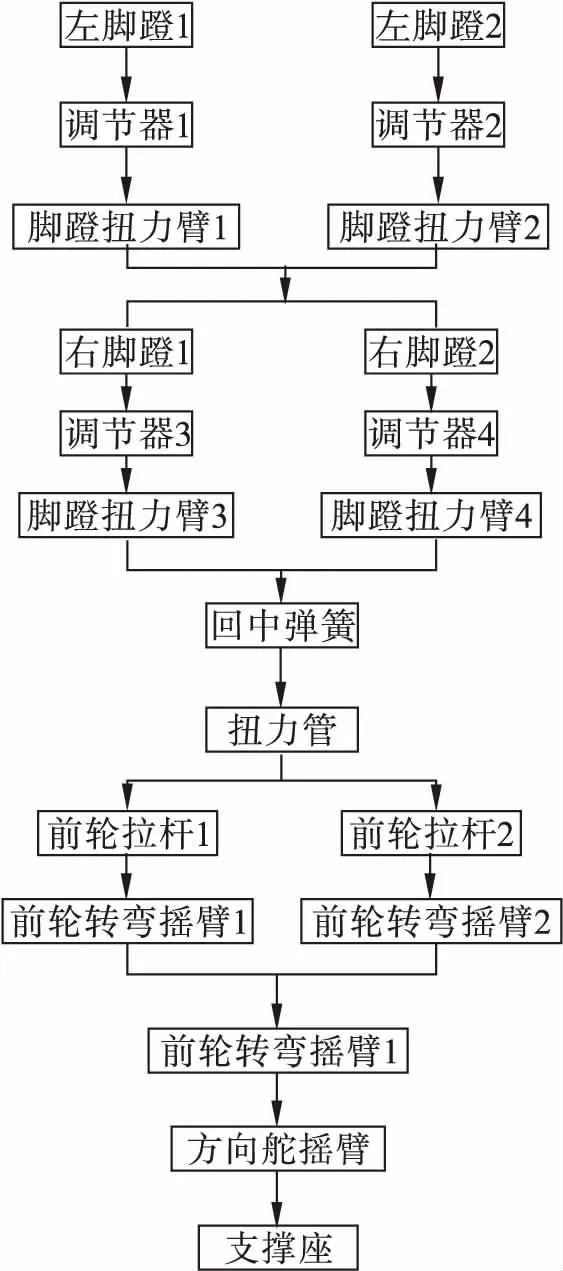
图2 脚蹬系统可靠性模型框图
2 成本函数和广义成本函数
可靠性分配由飞机各系统的复杂性、重要度、技术成熟度、使用环境等因素决定,最终表现为飞机的研制成本[14]。脚蹬系统可靠性指标根据电动飞机设计指标确定后,将其按照一定的规则分配给各组成单元的过程就是可靠性分配设计。
目前人们一直在研究与实际研制项目成本相对应的研制成本管理函数的计算模型,许多专家学者已经提出不同的研制成本计算函数。文献[5]中构建了一个成本函数模型如式(1)所示
(1)
其中:fi为对应部件的技术可行度,Ci(Ri)为第i个单元的成本,Ri为第i个单元分配的可靠度,Ri,min为Ri的最小可靠度,Ri,max为Ri的最大可靠度。
尽管式(1)能够表示与实际的研制成本表现出来的情况基本趋势,但忽略了部件的重要度和技术可行度的影响。另外没有考虑到单个部件的具体价格,影响了模型的应用。
文献[8]基于曲柄连杆机构的实际特性,结合部件重要度和技术可行度对成本模型进行了改进,构建了广义成本函数的概念
(2)
其中:cri为对应部件的重要度。
由式(2)可以看出,可行度取值范围在0~1。该部件提升的可行度与广义成本值成负相关,对应结果符合实际成本的基本要求。但公式(2)中对部件重要度的定义是基于部件所起作用和所处环境下,对部件可靠程度要求。部件重要度变化与广义成本的关系如图3所示。

图3 重要度变化与广义成本函数的关系
由图3可以看出:随着部件重要度的增大,广义函数是减小的,这样的变化趋势与实际情况相反。因此,广义成本函数实际上是与系统中重要部件的可靠度分配相关联的函数。
鉴于本文研究目的是期望得到脚蹬系统可靠度分配与实际研制成本的关系,因此,本文对式(2)进行修改,引入部件的成本系数,如式(3)所示
(3)
式(3)中,ki为第i个部件的成本系数。
部件的成本系数体现了部件在整个系统中成本所占比例。这样就可以通过权重系数区别在其他参数相同的情况下,不同价格部件对应的成本函数值。
借鉴文献[8]重要度的概念,部件的重要度表征的是该部件在系统中的重要程度,由所处的环境因素与故障危害的程度划分,重要度的范围定为[0.1,1.0]。因此,成本函数最终如式(4)所示
Ci(Ri,fi,Ri,min,Ri,max,ki)=kicri(1-fi)
(4)
这样处理是考虑其他参数相同时,重要度高的部件提高可靠度的成本要高。不同成本系数与改进后的成本函数关系如图4所示,通过价格系数可以很明显地区分不同部件。
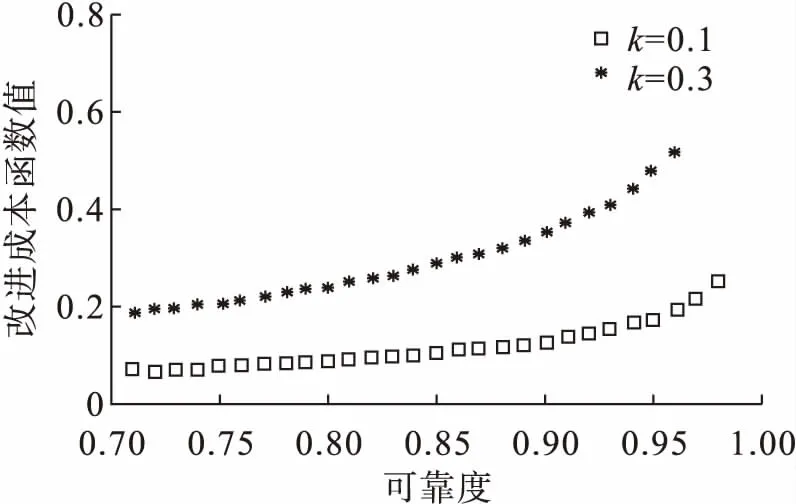
图4 成本系数变化与改进成本函数的关系
在改进成本函数的基础上,本文采用遗传算法对电动飞机脚蹬系统的可靠性分配问题进行优化设计。
3 遗传算法优化过程及结果
遗传算法是目前工程上比较常用的一种现代优化方法。它的基本操作包括编码、产生初始种群、计算目标函数、判断是否满足优化条件等过程。
电动飞机脚蹬系统可靠性分配优化设计以研制成本为目标函数,建立可靠性分配优化模型如下
(5)
式(5)中:RS为飞机的可靠度,RG为飞机的可靠性指标。
通过分析和计算得到的参数如表1所示。部件的重要度是按照部件受力情况综合得到的;部件的成本系数是按照给出的价格计算而来的。其中,部件的价格是参照市场最高价给出的。
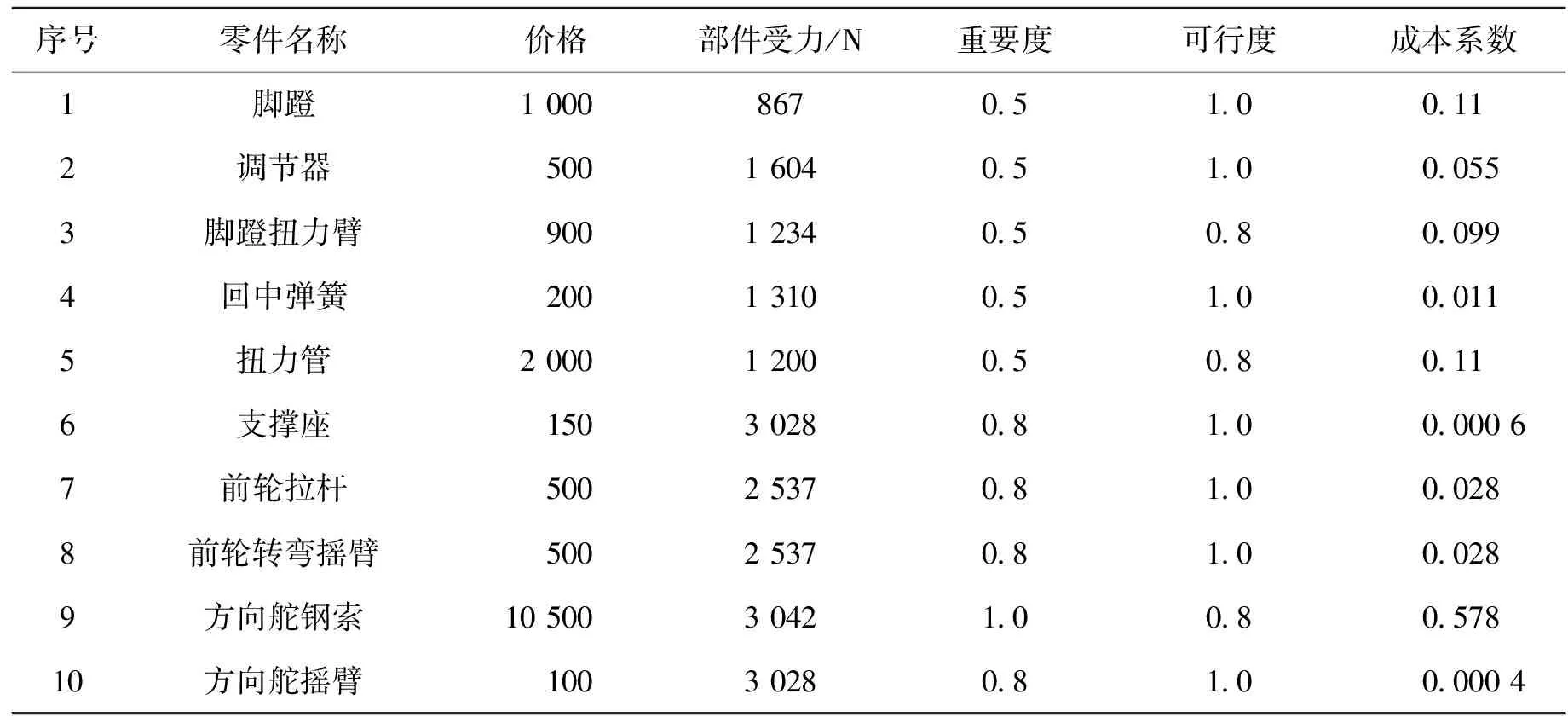
表1 脚蹬系统部件参数
在遗传算法中,目标函数对遗传算法的影响很大,它是用遗传算法对参数进行寻优的指标。而对目标函数值的使用是通过评价个体的适应度来体现的。针对脚蹬系统可靠性分配模型特点,选择式(5)作为本文优化的目标函数,以脚蹬系统总体可靠度不小于0.9作为限制条件。为了对比分析的需要,本文在相同参数和条件下,分别采用文献[5]和文献[13]中的方法对电动飞机脚蹬系统可靠性分配问题进行优化,所用目标函数分别是式(1)和式(2)。
在系统采用遗传算法取得优化结果过程中,考虑到需要优化的值参数范围较广,为了快速得到合理的优化结果选用优化个数为100,可靠度要求取得的值参数范围可以统一设定为[0.95,0.999]。采用二进制编码,经过2000代寻优,交叉和变异概率分别为pc=0.6和pm=0.2,得到目标函数的优化结果。为了分析系统可靠度分配方法的特点,本文分别采用文献[5]、文献[13]和本文的方法,优化参数相同的条件下,得到的结果如表2所示。

表2 可靠度优化结果
由表2的优化结果可以看出,文献[14]的方法注重部件重要度的影响,因此,对重要度要求较高的部件分配的可靠度比较高,例如方向舵钢索、方向舵摇臂等部件。但该方法对系统的成本因素考虑较弱。本系统中尽管方向舵钢索的重要度较高,但其价格占到整个系统的57.8%,这样的选择显然没有考虑系统成本。文献[12]基于部件可行性角度进行系统可靠性分配,因此,对应可行度比较大的部件可靠性分配的较高。例如回中弹簧、支撑座、方向舵摇臂等。但是,文献[13]方法中没有考虑部件重要度和实际成本因素对可靠度分配的影响。由优化结果可以看出,本文方法是基于在满足系统可靠度的基础上使系统总成本最低,优化结果是部件成本系数较低的部件可靠度分配的较高。也就是说,本文方法是基于系统成本考虑,采用提高成本系数较低部件的可靠度,降低成本系数较高部件的可靠度的方法来增加整个系统的可靠度。例如,方向舵钢索和扭力管成本占整个系统成本比例较高,可靠度分配的最低[15]。
以上分析表明,上述3种方法从不同侧重点进行系统的可靠度分配。但只有本文方法最后优化结果得到了整个系统的成本指数,可以很直观地考察脚蹬系统的实际成本。文献[5]的方法考察广义成本函数,尽管建立了部件重要度和可靠度分配的联系,但与实际的成本存在的误差较大。把本文和文献[5]的研究方法相结合,修改重要度较高的分系统可靠度取值范围就可以得到相应的可靠度分配优化结果,具体结果如表3所示。图5为遗传算法寻求最优解流程图,图6为遗传算法目标函数的最优收敛曲线,

表3 修改取值范围的可靠度优化结果
图5 遗传算法寻求最优解流程图

图6 遗传算法优化结果
从表3可以看出,采用本文方法也能够兼顾重要度高的分系统,满足系统的需求,同时还获取了有关脚蹬系统的成本指数和可靠度分配等具有重要参考价值的信息。
4 结论
本文根据电动飞机脚蹬系统部件设计的基本要求,参照了当前广义成本计算函数的设计特点,在当前广义成本计算函数的设计基础上,分别介绍了成本计算系数与脚蹬系统部件重要度,重新构建一个能够较好地描述脚蹬系统成本特性的成本函数。通过建立的成本函数用作电动飞机脚蹬系统可靠性分配方式的目标函数,以脚蹬系统可靠度为优化的约束条件,结合遗传算法进行了脚蹬系统可靠度分配优化研究,并对设计结果进行分析。分析设计结果表明:本文构建的成本函数参数的取值与实际工程设计要求关联紧密,本文的设计方法方便灵活,为电动飞机的可靠度分配方面提供了参考方案。
