利用GPR早期信号振幅属性监测土壤含水率①

吕 恒，聂俊丽，王智慧，张力文，窦勇硕

利用GPR早期信号振幅属性监测土壤含水率①

吕 恒1，聂俊丽2*，王智慧2，张力文2，窦勇硕2

(1贵州大学资源与环境工程学院，贵阳 550025；2贵州大学国土资源部喀斯特环境与地质灾害重点实验室，贵阳 550025)

为了研究GPR早期信号振幅属性与土壤含水率的关系，建立物理模型并配制了7组不同含水率的土壤，采用300、400和900 MHz GPR天线进行探测。选取GPR第一峰值信号、第一正半周期、第一半周期3种典型时段早期信号，利用希尔伯特变换计算平均振幅包络并求倒数，与烘干法测量所得土壤含水率结果进行对比，拟合出平均振幅包络倒数与土壤含水率之间的关系式。3种典型早期信号的振幅包络的倒数与土壤体积含水率均为线性相关，相关系数分别为0.883、0.926、0.867，其中第一正半周期内的振幅包络的倒数与土壤体积含水率拟合效果最好，含水率平均相对标准差为0.483%，通过土壤介电常数试验结合Topp公式计算得到的体积含水率与实测体积含水率平均相对标准差为1.069%。结果表明利用平均振幅包络倒数法研究第一正半周期内雷达波平均振幅包络倒数得到的土壤含水率较为精确。

GPR早期信号；土壤含水率；希尔伯特变换；平均振幅包络

土壤含水率是影响土地复垦的主要因子之一，准确监测土壤含水率时空分布对生态修复有重要意义。传统的土壤含水率测定方法通过开挖土壤剖面或钻孔取样，实验室测量或通过便携式仪器如时域反射仪(time-domain reflectometer，TDR)等获取，虽然这些传统探测方法能够得到精确的地下土壤的结构特征和土壤含水率，但仅限于小尺度范围内[1-2]。要得到较大区域范围的土壤含水率时空分布不仅费时费力，而且还会出现以点代面的情况。近年来，探地雷达(ground penetrating radar，GPR)已被应用于中尺度范围内土壤含水率的探测研究中，其中探地雷达地面波法、折射波法等探测土壤含水率均需要计算波速，进而获取介质的介电常数，再由Topp公式等经验公式计算含水率值[3]。常见的经验并不适用于所有类型的土壤，而且会造成误差的二次传递，从而影响含水率测量的精度。相比于雷达波波速分析求土壤含水率方法，Pettinelli等[4]提出了一种利用平均振幅包络倒数(average envelope amplitude，AEA)方法，计算认为雷达早期信号的平均振幅包络与浅部地层介电常数呈负相关关系，从而计算出土壤的介电常数，再由Topp经验公式计算含水率值[5]。Di Matteo等[6]利用AEA法分析室内模型和野外数据的早期信号振幅属性的变化，证明该方法能够很好地反映土壤含水率的变化；Pettinelli等[4]在野外对AEA方法进行了验证，结果表明雷达波早期振幅包络与介电常数有着高度的相关性，但并没有对该方法的适用条件进行阐述。

在国内，吴志远等[7]利用AEA方法在野外进行地表含水率探测，找出与介电常数相关系数大的振幅包络倒数平均值，利用Topp公式计算出土壤含水率并与TDR和钻孔取样探测的地表含水率进行对比，表明使用探地雷达 AEA方法能够能得到与TDR及取样烘干实测含水率相近的土壤含水率。乔新涛等[8]采用AEA法对复垦区农田地块土壤含水率进行反演，并与雷达测线上TDR法测量所得土壤含水率结果进行对比，认为研究的4种关系模型中对数模型的拟合结果最好。

前人研究是利用雷达信号包络平均值求出介电常数，然后再采用Topp公式等经验公式进一步估算含水率，这容易将误差进行二次传递。本文是在前人的研究基础上，通过物理模拟试验研究第一峰值信号、第一正半周期和第一半周期3种典型的GPR早期信号[6]平均振幅包络值和土壤含水率的直接相关性，拟合找出3种早期信号中相关性最强的早期信号，快速获取大范围内土壤含水率值。

1 方法原理

1.1 数值模拟试验

利用Giannopoulos[9]开发的开源软件GprMax建立土壤模型控制体积含水率(volume moisture content，VMC)分别为5、10、15、20 和25 cm3/cm3，激励源选择主频为400 MHz的雷克子波，模拟出不同含水率的土壤对应的雷达剖面，选取单道信号振幅，分析土壤含水率的变化对雷达波早期信号振幅的影响。

1.2 土壤类型及物理模拟试验

1.2.1 土壤类型测试 利用紫外可见分光光度计测量试验土样颗粒粒径，黏粒(<2 µm)、壤粒(2 ～ 20 µm)、砂粒(20 ～ 2 000 µm)分别为4.5%、48.5%、47%。对照国际制土壤质地分类标准[10]确定试验土样为壤土，再根据中国土壤分类系[11]，结合农业生产方面分类，试验土样应属六级分类制中土类红壤。

1.2.2 土壤含水率物理模拟 共设置7种不同含水量的物理模型，模型箱大小为1.2 m × 0.8 m × 1 m。分别用300、400、900 MHz 3种不同频率的中高频天线沿测线方向(图1)对模型箱土壤含水率采用共偏移距方法进行探测，目前，国际上应用GPR探测土壤含水率时采用225 ～ 900 MHz的中高频天线[12]，225 MHz以下的低频天线尺寸较大，分辨率较低不适合土壤含水率物理模拟试验，中高频天线在保证探测精度的同时也兼顾一定的探测深度。测完后在模型剖面方向打标处从上至下间隔10 cm依次用环刀连续取10个样以及对应的平行样。取样结束后从模型箱里取出土样用洒水壶喷水，并搅拌均匀，再装入模型箱按照上述试验数据采集取样步骤完成其他组试验。第一组试验对采集的原状土样进行探测。由于水量人为控制，后面几组试验视土壤湿度控制喷水量，采集完7组不同含水量的雷达剖面，最后将所取样品带回实验室用烘干法测样品的土壤含水率，以及土壤容重等参数。

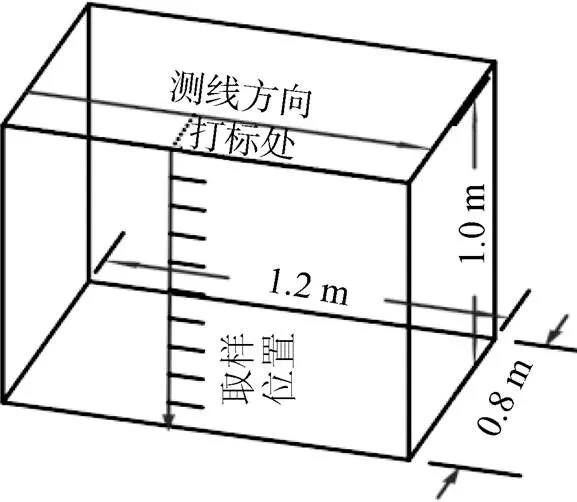
图1 含水率试验模型箱示意图

1.2.3 土壤介电常数物理模拟 利用GPR反射波法，测量电磁波在不同土壤含水率中的传播速度，再根据速度与介电常数之间的关系确定不同含水率土壤的介电常数，将求得的介电常数代入Topp公式并与烘干法测量的结果进行对比。本试验选择一个0.45 m × 0.32 m × 0.25 m的小塑料箱建立物理模型(图2)，并在塑料箱底部放置一块金属板，以便实现对电磁波的全反射，获取电磁波在已知厚度的土壤层中的双程旅行时，用于计算土壤的介电常数。

图2 介电常数试验模型箱

1.3 反演土壤含水率原理

1.3.1 反射波法反演土壤含水率 利用GPR反射波法测量不同含水率的土壤介电常数，电磁波的传播速度会随着介质介电常数的增加而减小，当遇到良导体时，电磁波便会发生全反射。雷达波在土壤中的传播速度与土壤的介电常数存在以下关系，即：

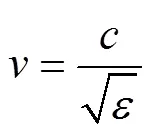
式中：为雷达波在真空中的传播速度(0.3 m/ns)，为土壤的相对介电常数。

因此，只需要求得电磁波在土壤中的传播速度，便可通过式(1)计算得到土壤的相对介电常数。利用GPR反射波法，在已知测量土壤厚度的情况下，根据电磁波在介质中的双程旅行时间，可以根据式(2)求得电磁波在土壤中的传播速度。

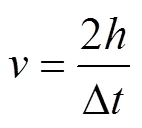
由公式(1)、(2)便可计算出土壤的介电常数：

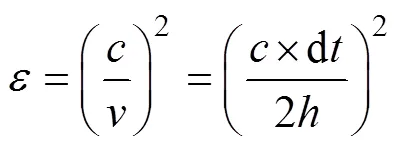
将公式(3)计算得到的介电常数带入Topp公式(公式(4))等–经验公式便可反演得到土壤体积含水率。

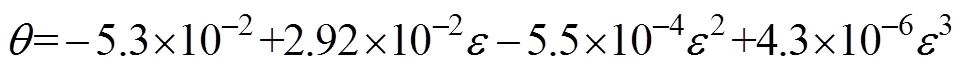
式中：为土壤体积含水率(cm3/cm3)，为土壤介电常数。

1.3.2 AEA法反演土壤含水率 电磁波在介质中传播时，振幅会受到周围介质中电磁波性质的影响，随着传播距离增加，其振幅相对于初始振幅0呈指数衰减[13]，具体计算公式如下：

=0e–αz(5)

对于低损耗介质是与频率无关的，因此由上式可以看出介电常数对振幅影响很大。水的介电常数为81，土壤的介电常数一般为3 ～ 25，利用土壤和水的介电常数差异得到不同土壤含水率对应的电磁波早期振幅信号，通过希尔伯特变换[14]得到振幅包络，设GPR得到的原始连续信号为()，对其进行希尔伯特变换，其变换公式如下：

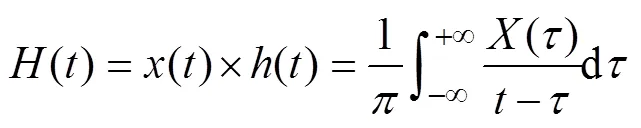
信号数据经过希尔伯特变换后，相位谱要作 90°相移，相当于一次滤波，以() 为实部，以() 为虚部，构建解析信号[15]：

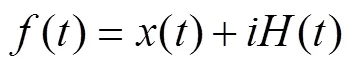
则振幅包络为：

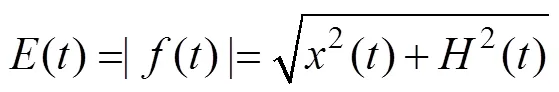
求得的振幅包络为正值，它使GPR单道信号变得简化，让振幅更容易被解释。将变换后的数据用matlab程序计算得到雷达各单道振幅包络值，选取取样附近的单道数据求得平均振幅包络倒数。

2 结果与分析

2.1 数值模拟结果

模拟出的雷达波早期信号振幅的变化情况以及通过希尔伯特变换后得到的振幅包络如图3所示，从中可以看出，当土壤含水率较低时，微小的含水量变化就会导致振幅有很大的波动，而当土壤含水率较高时，即使含水量变化很大但振幅的波动并不明显。因为土壤含水率越高，电磁波衰减越快，这也就导致了GPR实际探测精度降低[16-20]。

根据GPR早期信号对应的时间窗口段内的所有单道振幅包络值求平均，然后选取第一峰值信号、第一正半周期和第一半周期3种早期信号进行研究。如图4所示，利用gprMax模拟这3个GPR早期信号对应的时窗内单道波形及相应的希尔伯特振幅变换。

2.2 物理模拟结果

2.2.1 土壤体积含水率 利用烘干法测得土样的质量含水率，根据土壤质量含水率、土壤容重和土壤体积含水率之间的关系，利用式(9)计算得到土壤体积含水率，并作出土壤体积含水率分布图(图5)。

式中：v为土壤体积含水率(cm3/cm3)，w为土壤质量含水率(g/g)，b为土壤容重(g/cm3)。

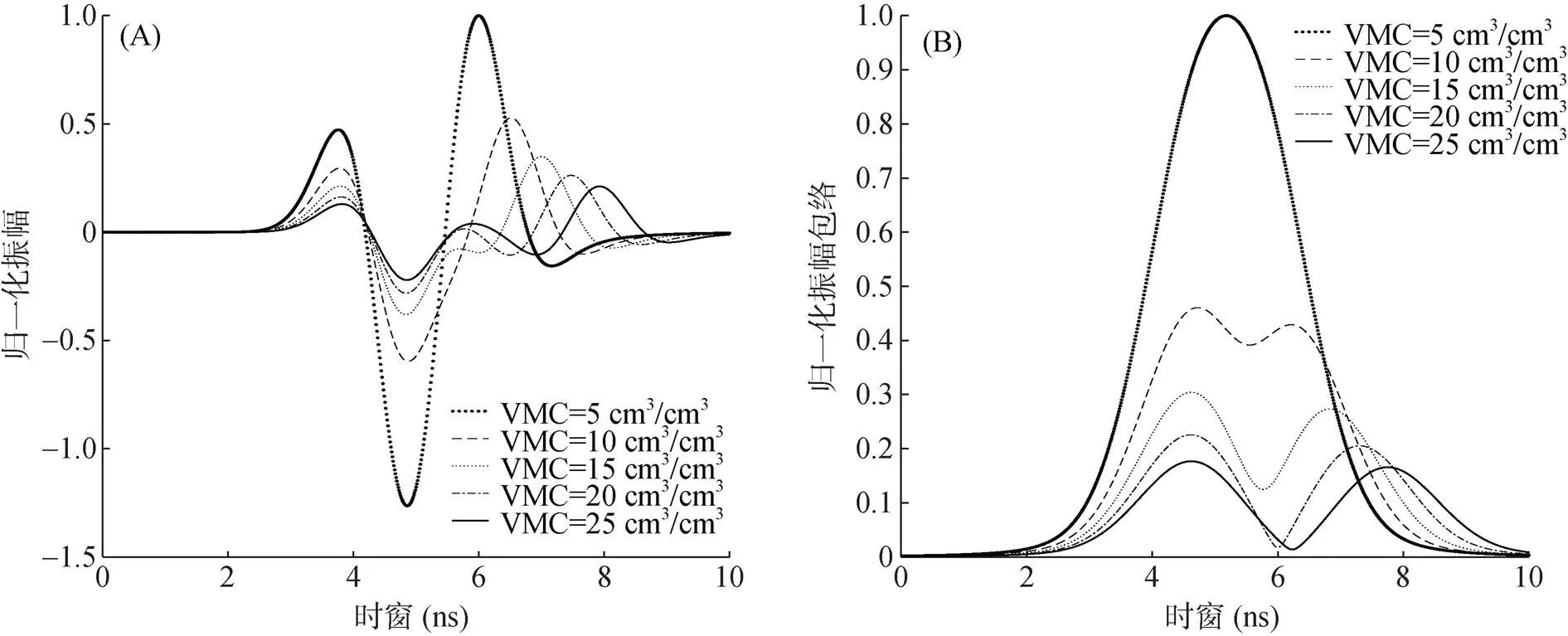
图3 土壤体积含水率(VMC)与GPR早期信号单道波振幅(A)、单道波振幅包络(B)之间的关系

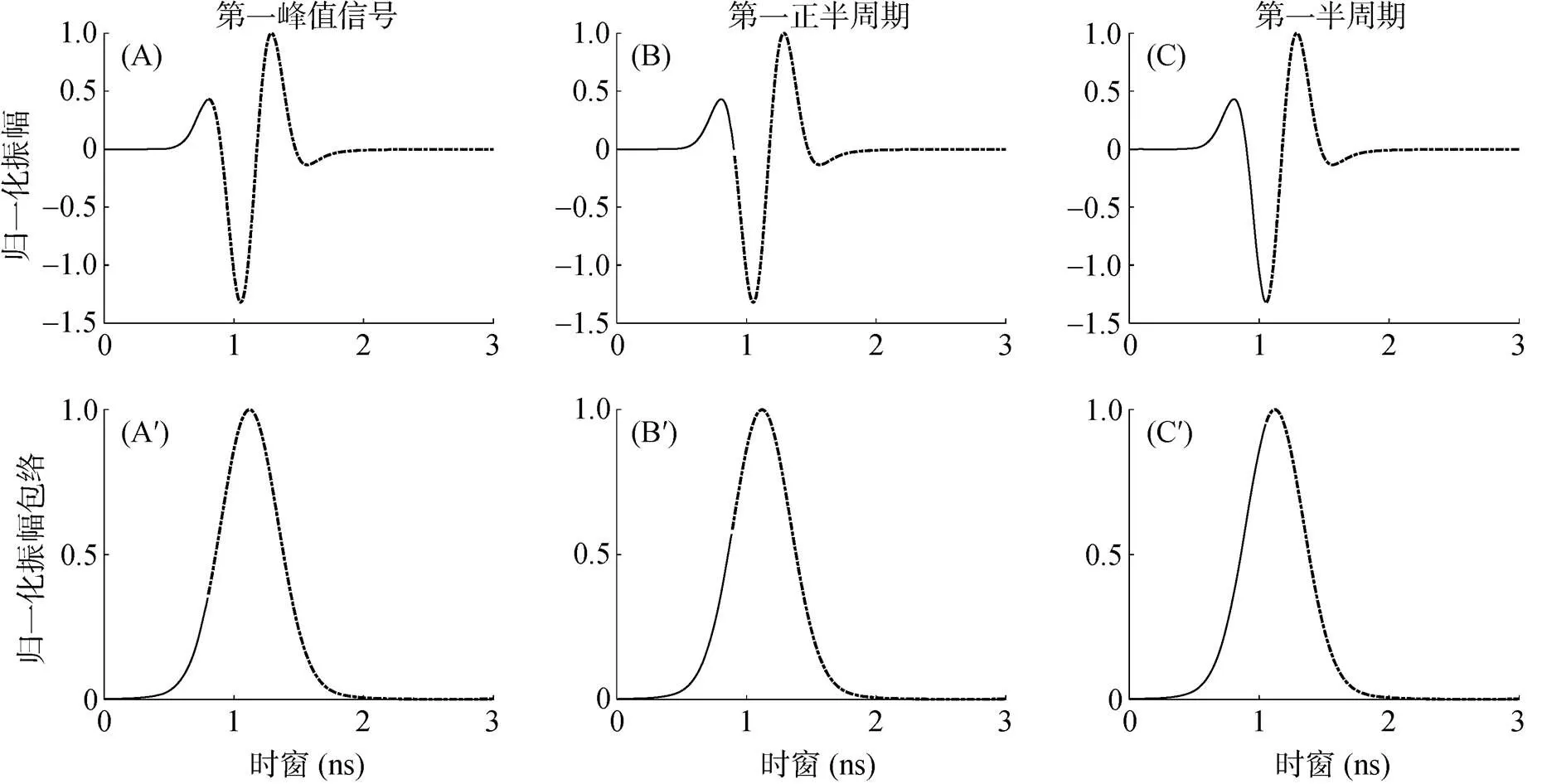
(A和A′, B和B′, C和C′粗线分别表示第一峰值信号、第一正半周期和第一半周期)

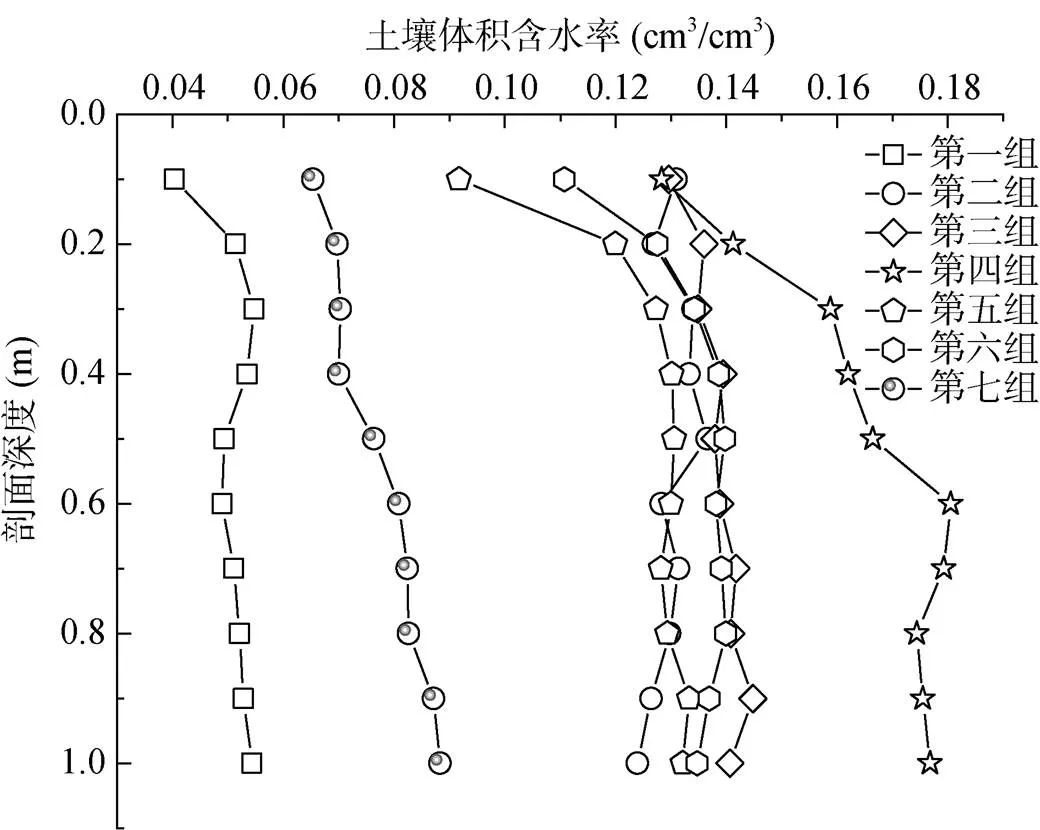
图5 土壤体积含水率剖面分布

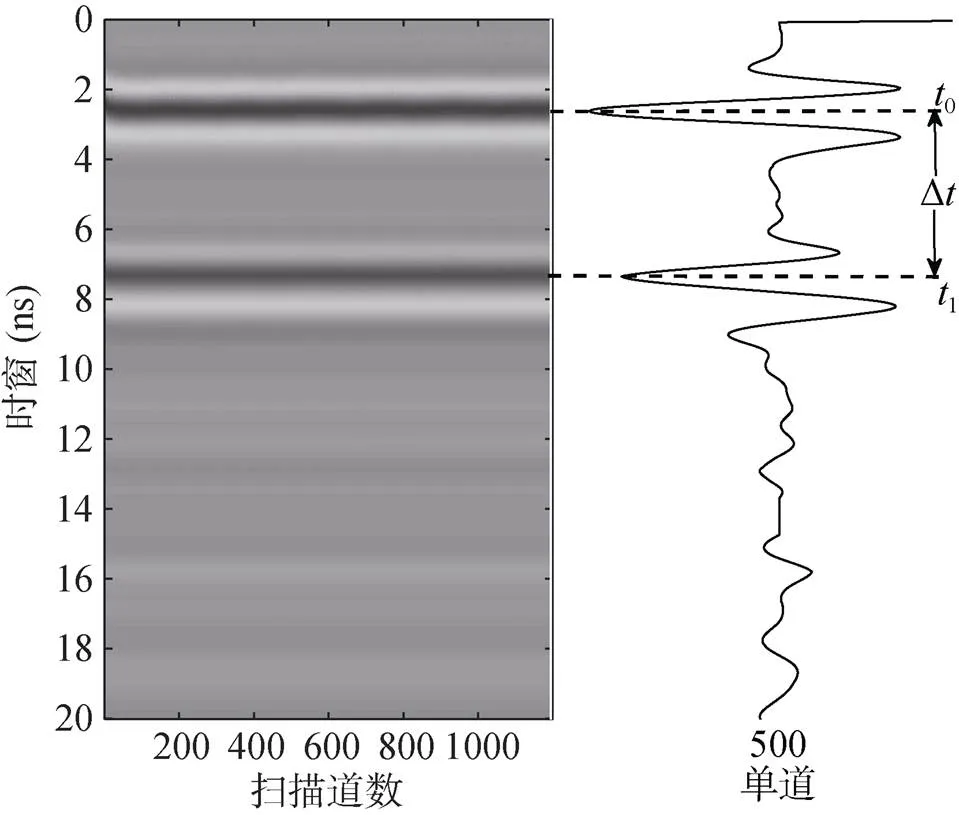
图6 红壤土雷达剖面及单道图

通过探测不同含水率土壤得到不同的雷达剖面，提取取样附近雷达剖面单道数据读取电磁波在不同含水率土壤中传播的双程旅行时，根据公式(3)得到不同含水率土壤的介电常数，将计算得到的介电常数带入Topp公式得到土壤预测体积含水率。介电常数试验相关参数见表1。

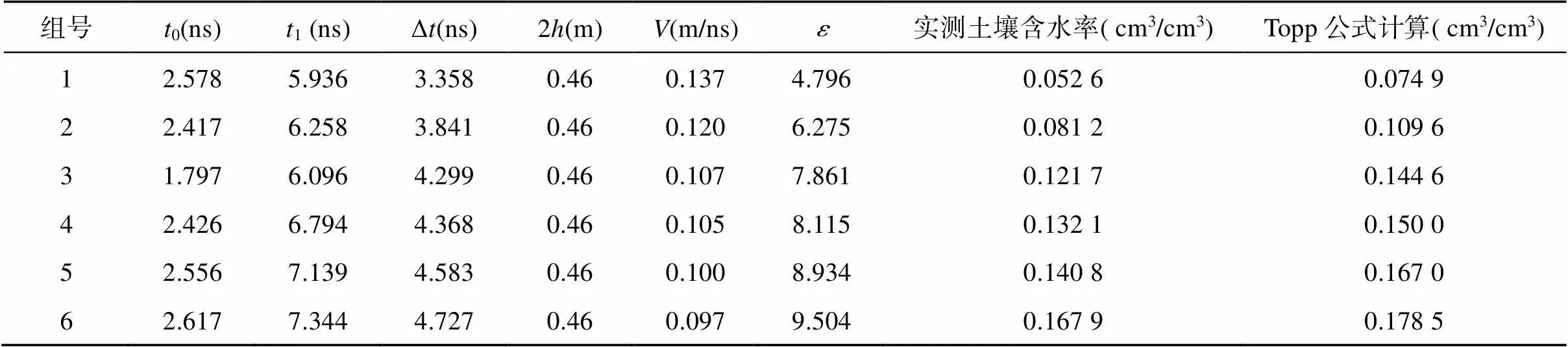
表 1 介电常数试验相关参数

从图7A中可以看出，Topp公式整体高估了土壤的体积含水率，对实测土壤含水率和Topp公式计算得到的土壤含水率进行误差分析（图7B），平均相对标准差为1.069%。说明Topp公式多适用于描述颗粒粒径较大的土壤类型(如砂土)的介电常数与体积含水率的关系，此外Topp公式需要计算介电常数来反演土壤含水率，这会造成误差的二次传递，这也是Topp公式高估了土壤体积含水率的一个重要因素。

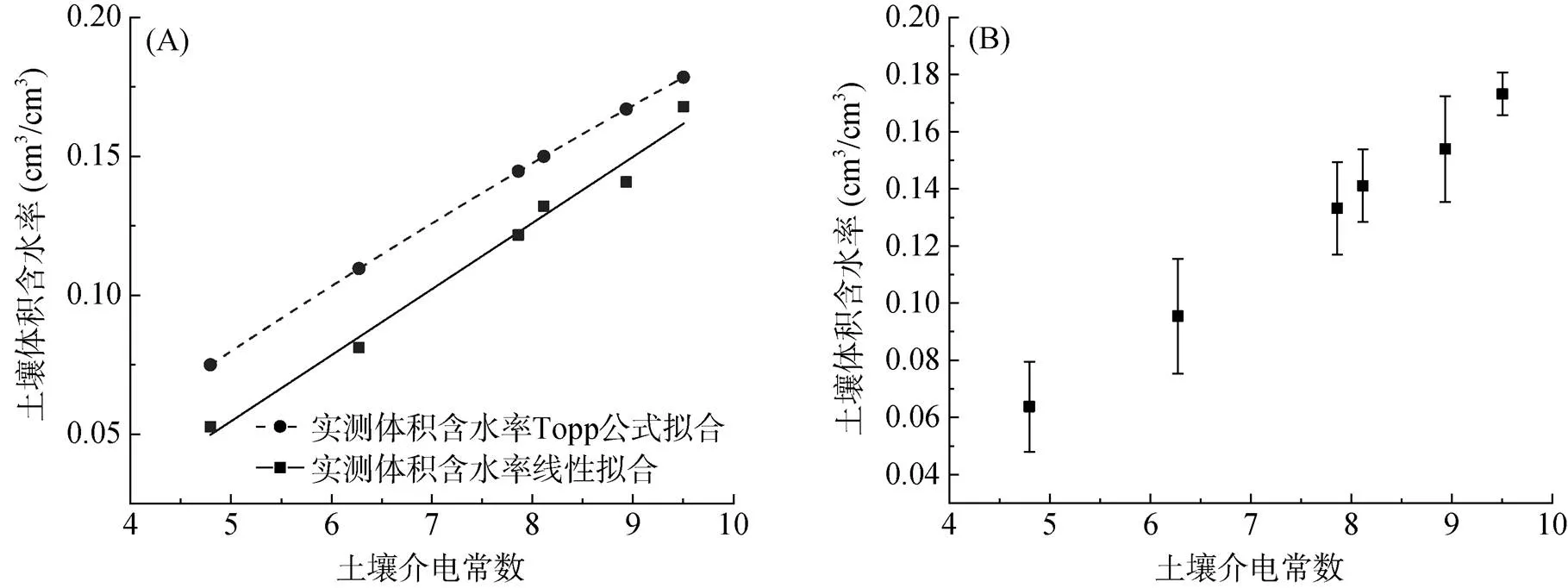
图7 红壤土介电常数与体积含水率拟合图(A)以及误差分析图(B)

2.2.3 AEA法试验结果 首先对模型箱内采集的雷达数据通过零点校正、背景去噪、一维滤波等常规处理后，提取单道波形，对每种天线采集的7组数据对比分析。如图8所示，通过归一化处理，可以看出不同含水率土壤早期振幅信号起跳点不同，含水率越低，起跳点越早，振幅越大，如图中黑色虚线代表模拟试验第一组对原状土探测所得的雷达波单道振幅[21]。随着时间的推移，电磁波信号衰减到越来越弱，对应的雷达波单道振幅信号越来越小，振幅不再有较大波动，雷达波单道振幅曲线接近重合，意味着无法监测深部土壤含水率。

对实际探测单道波形进行希尔伯特变换，从图8可以看出通过希尔伯特变换后的振幅变得更加简化。读取第一峰值信号、第一正半周期和第一半周期对应的时窗范围，并进行振幅包络计算，得到平均振幅包络倒数。选取第二组数据作为验证，拟合其他6组雷达波振幅包络倒数与烘干法测得的土壤体积含水量之间的关系[22]，如图9所示。

根据图9可以直观地看到第一正半周期内的振幅包络的倒数与土壤体积含水率拟合效果最好，表2给出了第一正半周期内振幅包络的倒数与土壤体积含水率的拟合关系式。

将第二组试验得到的平均振幅包络倒数代入表2中的拟合关系式得到土壤体积含水率，并与烘干法测得的土壤含水率进行比较，作出3种早期信号内土壤体积含水率误差分析图，从图10可以看出，第一正半周期内误差最小，体积含水率平均相对标准差为0.483%，因此可以利用第一正半周期振幅包络倒数计算红壤土的体积含水率。

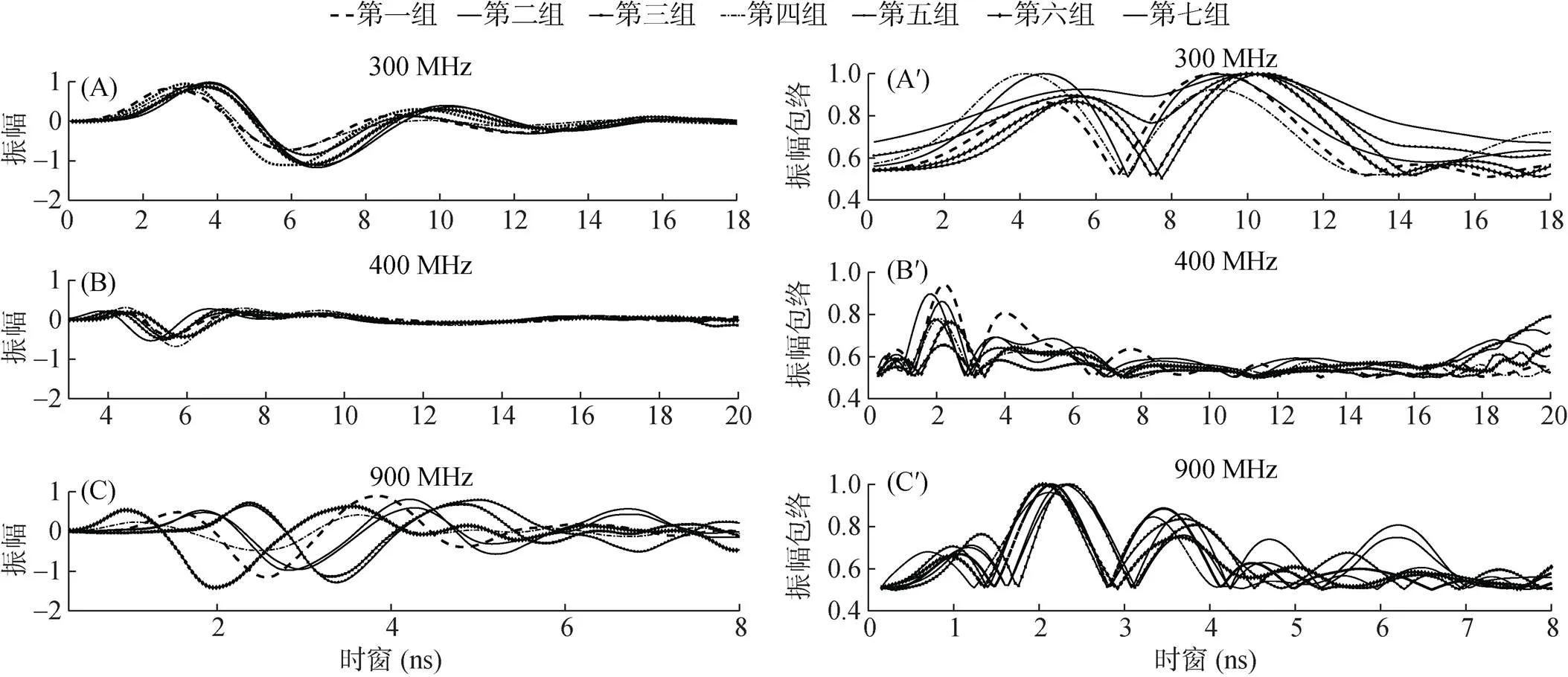
(A和A′, B和B′, C和C′分别表示3种天线探测得到的7组GPR单道波形及其相应的希尔伯特变换振幅包络 )

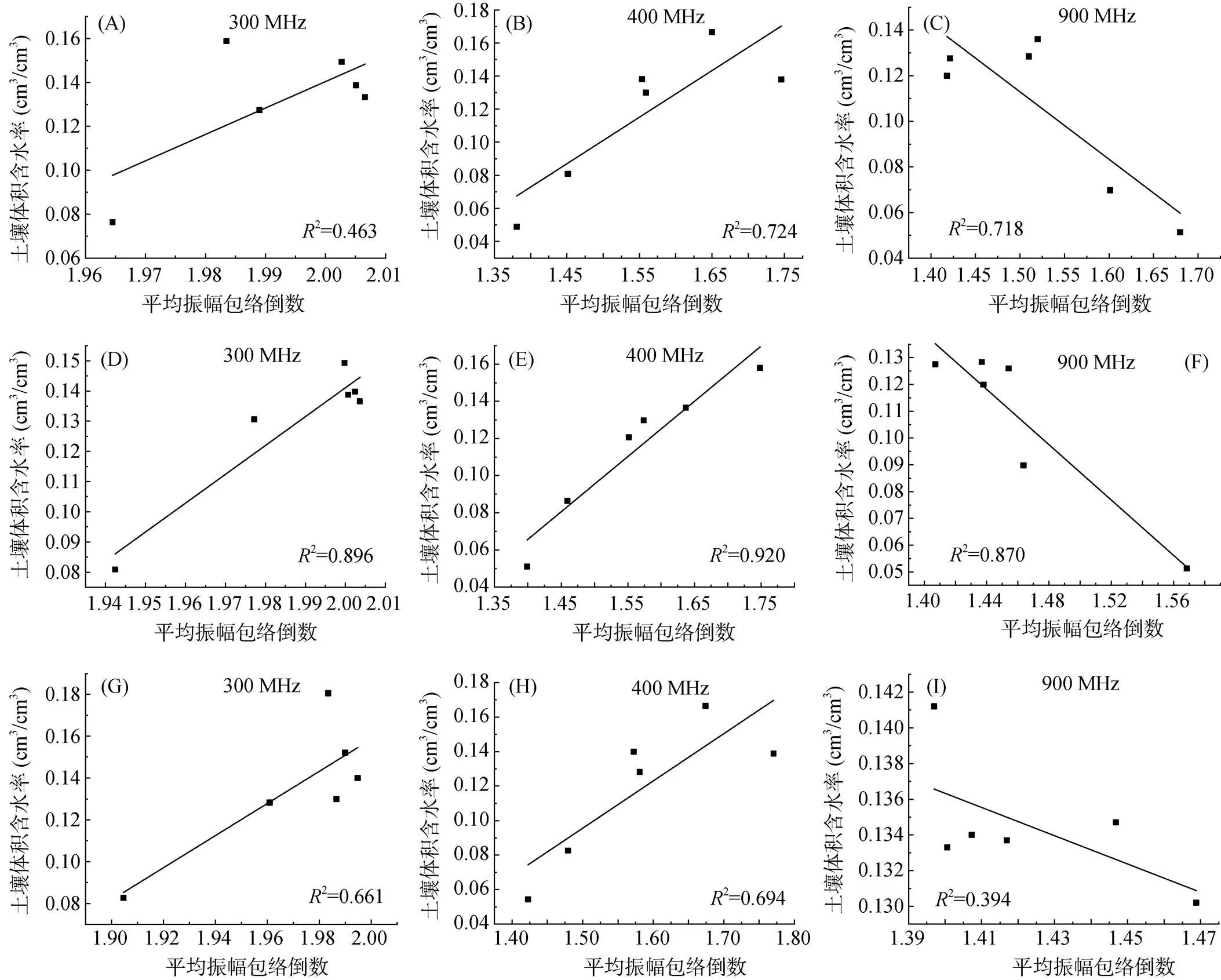
((A,B,C)、(D,E,F)、(G,H,I)分别是第一峰值信号内、第一正半周期内、第一半周期内AEA–1与VMC的拟合结果)

表2 第一正半周期内振幅包络倒数与土壤体积含水率拟合结果

注：式中为土壤体积含水率，为振幅包络倒数。

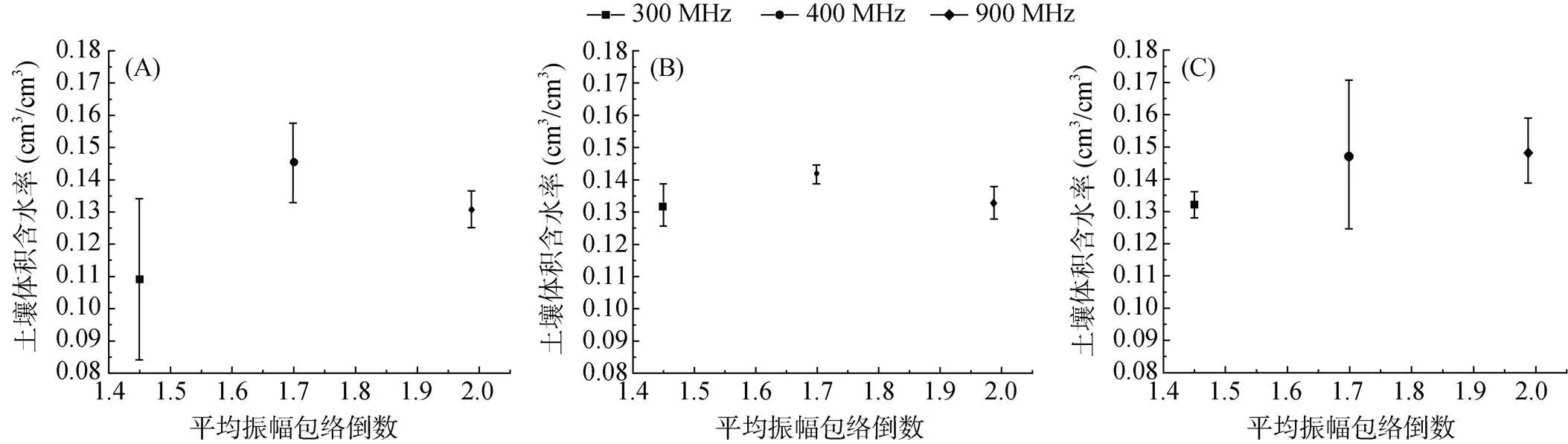
(A,B,C分别为第一峰值信号、第一正半周期和第一半周期内土壤体积含水率误差分析图)

3 结论

1)对于3种不同频率的天线，研究的3种时段的早期信号中第一正半周期内雷达波平均振幅包络的倒数与土壤体积含水率有较好的线性关系，300、400、900 MHz天线探测数据计算的土壤含水率与烘干法测得的土壤含水率标准差分别为0.506%、0.289%、0.656%，平均相对标准差为0.483%。

2)土壤介电常数试验结果表明Topp公式高估了土壤的体积含水率，实测土壤体积含水率与Topp公式计算得到的体积含水率平均相对标准差为1.069%。结果表明利用AEA法研究第一正半周期内雷达波平均振幅包络倒数得到的土壤含水率较为精确。

3)本文研究不通过估算土壤介电常数就可以直接利用GPR第一正半周期振幅包络倒数快速计算土壤体积含水率，对于农业生产、土地复垦具有重要的指导意义。

[1] 雷少刚, 卞正富. 探地雷达测定土壤含水率研究综述[J]. 土壤通报, 2008, 39(5): 1179–1183.

[2] 卢奕竹, 宋文龙, 路京选, 等. 探地雷达测量土壤水方法及其尺度特征[J]. 南水北调与水利科技, 2017, 15(2): 37–44.

[3] 王春辉, 刘四新, 仝传雪. 探地雷达测量土壤水含量的进展[J]. 吉林大学学报(地球科学版), 2006, 36(S1): 119–125.

[4] Pettinelli E, Vannaroni G, di Pasquo B, et al. Correlation between near-surface electromagnetic soil parameters and early-time GPR signals: An experimental study[J]. Geophysics, 2007, 72(2): A25–A28.

[5] Topp G C, Davis J L, Annan A P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines[J]. Water Resources Research, 1980, 16(3): 574–582.

[6] Di Matteo A, Pettinelli E, Slob E. Early-time GPR signal attributes to estimate soil dielectric permittivity: A theoretical study[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(3): 1643–1654.

[7] 吴志远, 彭苏萍, 杜文凤, 等. 基于探地雷达波振幅包络平均值确定土壤含水率[J]. 农业工程学报, 2015, 31(12): 158–164.

[8] 乔新涛, 曹毅, 毕如田. 基于AEA法的黄土高原矿区复垦农田土壤含水率特征研究[J]. 土壤通报, 2019, 50(1): 63–69.

[9] Giannopoulos A. Modelling ground penetrating radar by GprMax[J]. Construction and Building Materials, 2005, 19(10): 755–762.

[10] 吴克宁, 赵瑞. 土壤质地分类及其在我国应用探讨[J]. 土壤学报, 2019, 56(1): 227–241.

[11] 黄鸿翔. 我国土壤分类四十年的发展道路[J]. 土壤肥料, 1989(4): 1–6.

[12] Huisman J A, Snepvangers J J J C, Bouten W, et al. Mapping spatial variation in surface soil water content: Comparison of ground-penetrating radar and time domain reflectometry[J]. Journal of Hydrology, 2002, 269(3/4): 194–207.

[13] 聂俊丽. 基于地质雷达技术的采煤对浅部地层含水量影响规律研究[D]. 北京: 中国矿业大学(北京), 2014.

[14] 程乾生. 希尔伯特变换与信号的包络、瞬时相位和瞬时频率[J]. 石油地球物理勘探, 1979, 14(3): 1–14.

[15] 胡艳杰, 余湘娟, 高磊, 等. 探地雷达在道路结构层厚度检测中的应用[J]. 河北工程大学学报(自然科学版), 2017, 34(4): 37–41,56.

[16] 方慧, 魏文博, 李玉堂. 介质含水率与探地雷达信号关系数值模拟[J]. 物探与化探, 2009, 33(5): 533–535.

[17] Ferrara C, Barone P M, Steelman C M, et al. Monitoring shallow soil water content under natural field conditions using the early-time GPR signal technique[J]. Vadose Zone Journal, 2013, 12(4): vzj2012.0202.

[18] 曾昭发, 刘四新, 王者江. 探地雷达方法原理及应用[M]. 北京: 科学出版社, 2006.

[19] 刘四新, 曾昭发. 频散介质中地质雷达波传播的数值模拟[J]. 地球物理学报, 2007, 50(1): 320–326.

[20] 武彦斌, 崔凡, 王磊, 等. 透射式探地雷达探测土壤含水率[J]. 农业工程学报, 2014, 30(17): 125–131.

[21] 崔凡, 刘杰, 吴志远, 等. 探地雷达功率谱模型在砂壤含水率和紧实度探测中的应用[J]. 农业工程学报, 2014, 30(16): 99–105.

[22] 吴志远, 尹尚先, 马丽红. 基于探地雷达的煤矿开采区地表土壤含水率变化研究[J]. 华北科技学院学报, 2017, 14(6): 17–23.

Monitoring Soil Moisture Content Using Early-signal of GPR Amplitude

LÜ Heng1, NIE Junli2*, WANG Zhihui2, ZHANG Liwen2, DOU Yongshuo2

(1 College of Resources and Environmental Engineering, Guizhou University, Guiyang 550025, China; 2 Key Lab of Karst Environment and Geohazard, Ministry of Land and Resources, Guizhou University, Guiyang 550025, China)

In order to study the relationship between the amplitude of the early-time-signal of GPR and the soil moisture content , a physical model was established and seven groups of soils with different water contents were prepared. 300, 400, and 900 MHz GPR antennas were used for detection. Three typical periods of the early-time-signals of GPR (first signal onset, first positive half cycle and first half cycle) were selected to calculate volume moisture. Firstly, Hilbert transform was used to calculate the envelop amplitude, then the reciprocal of their average of the three corresponding periods were calculated respectively, finally the relationship between the reciprocal of the average envelope amplitude and the results of moisture measured by the drying method were fitted. All fitting results showed linear correlation and the correlation coefficients were 0.883, 0.926 and 0.867, respectively. But the reciprocal of the amplitude envelope in the first positive half cycle had the best fitting effect with soil volume moisture, and it’s average relative error of moisture content was 0.483%, the average relative standard deviation between volume moisture calculated by the soil dielectric constant test and the Topp formula and the measured volume moisture was 1.069%. In conclusion, it is more accurate to predict the moisture of soil by studying the reciprocal of the radar wave average envelope amplitude in the first positive half cycle with the AEA method.

Early-signal of GPR; Soil moisture content; Hilbert transform; Average envelope amplitude

吕恒, 聂俊丽, 王智慧, 等. 利用GPR早期信号振幅属性监测土壤含水率. 土壤, 2022, 54(1): 169–176.

S152.7

A

10.13758/j.cnki.tr.2022.01.022

新疆能源2030项目生态修复项目(GJNY2030XDXM-19-03.2)、陕煤集团重大项目 (2018SMHKJ-A-J-03)和校青年基金项目(贵大人基合字2014(62)号)资助。

(junlinienie@163.com)

吕恒(1996—)，男，甘肃天水人，硕士研究生，主要从事探地雷达探测土壤含水率方面的工作。E-mail: 918615761@qq.com