面向电力大数据的用电负荷分类及用户用电行为分析

韩明冲，钟建伟，陈 静，黄 明，张继学，鄢 蓓

（1.湖北民族大学 信息工程学院，湖北 恩施 445000；2.国网湖北省电力有限公司恩施供电公司，湖北 恩施 445000）

0 引 言

近年来，“智能配用电网络”一词在电气领域较为热门，它是为实现电力网的精细智能化管理而诞生的一种网络。因其优点较多，故近年来我国一直在大力推进智能配用电网络的建设。而对于近年来同样较为火热的智能电网而言，智能配用电是其发展中不可缺少的一个环节，通过分析用户的用电行为，可对用户侧进行智能优化，以提高供电侧电能的质量以及供电的可靠性，使得供电方和用电方实现双赢。配用电的对象是用户，属于智能电网的末端，其网络体积庞大、结构复杂。另外，配用电的业务类型也较多，这就造成用户用电行为分析难度较大。但由于前些年智能小区的流行，既提高了用户参与智能用电环节的积极性，又方便了电网对于用户侧的精细智能管理。又因近年来大数据技术发展迅速，为用户用电行为的分析提供了一条新的途径。由于不同家用电器的用电特性有差异，所以即便小区家庭中用电设备的种类繁多，也为其功能的实现提供了可能。对用户而言，实现智能用电可以合理控制家庭电器的使用，进而节省用电开支。对电网来说，通过对用户用电行为的分析，可以了解到用户的用电规律，做到对用电负荷的预测，进而制定合理的送电策略；还能方便进行能效的管理、客户分类、异常用电检测以及电力营销等，这对电网侧经济性的提高有着重大意义。另外，用户用电情况分析也为政府做出产业调整、经济调控等宏观决策提供了依据。

随着聚类技术的蓬勃发展，电气领域涌现出了较多基于聚类的机器学习研究。例如，张斌等人使用降维聚类技术分析电力负荷曲线；赵明等人把聚类技术应用于用电负荷峰谷平时段的划分；黄文思以气象因素为依据进行负荷预测。有待解决的问题主要包括电力用户细分和电力用户负荷预测。

综上所述，为了深度挖掘用户用电行为特性，提升居民在用电行为上的用电效率和电力企业在电力市场上的份额，本文采用了基于改进K均值聚类算法的用户用电行为分析方法，对用户用电数据进行预处理后再进行聚类；根据聚类结果对用户用电行为进行分析，为供电公司的营销策略提出改进意见。

1 聚类算法

1.1 K-means

K-means算法是聚类算法的一种。所谓聚类，就是根据某一标准（如距离准则）将研究对象中相似的部分划分成多个类的过程。每个类中对象的差异性和相似性要尽可能大。对于一个特征矩阵（样本数为N），该算法可以将其分割成K个簇（需要人为设定），且这些簇之间没有交集。同一簇中样本数归为一类，不同簇为不同类别的分类结果。

设定K值，算出聚类中心和簇中数据点间的间距并进行多次迭代，以得到最优聚类中心，其数量为K。算法距离的定义采用欧式距离。如图1中直线OB的长度即为O、B两点在三维空间中的欧氏距离，其计算公式为：

图1 三维空间的欧氏距离

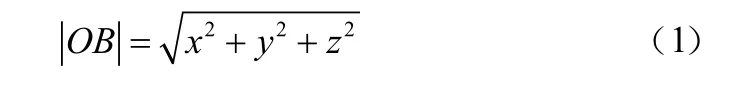
簇内的所有样本点到质点（聚类中心）距离的平方和的计算公式为：

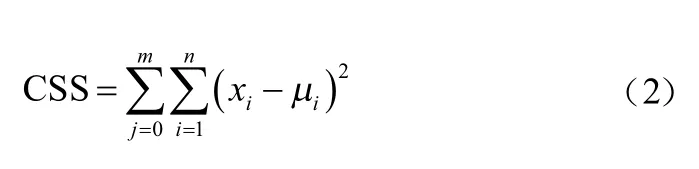
其中：为一个簇内样本数量；为每个样本点的特征数量；为某一簇内的样本点；为某一簇内的聚类中心；为组成点的每个特征；为每个样本的符号。

整体平方和（Inertia）为数据中所有簇内平方和之和，如式（3）所示。整体平方和值越小，表示每个簇中样本差异性越小，即聚类处理效果越佳。

结合以上计算过程及图2的算法流程可以看出，均值算法在选取聚类中心时，因具有随机性，故可能出现每次聚类结果差异较大的情况。针对此问题，需要对该算法进行一些改进。

图2 K-means算法流程

1.2 K-means++

因-means算法随机选择聚类中心，故可能使得最终聚类结果不理想，比如初始点都选在一个簇内。针对这一缺点，-means++算法诞生，主要是对初始聚类中心的选择做了改进。首先把值，即初始聚类中心数确定，然后进行聚类中心的选择。设算法已完成个中心的选取，在选择下一个中心时，若此点距离当前个中心点越远，则其被选概率越大。但如果为1，则此算法与未改进前一样，即聚类中心随机选取。换句话说，算法改进前后的区别在于对初始点的处理，确定好初始点之后，其余步骤都同未改进前一样。

首先随机选择初始聚类中心，然后计算出聚类中心与每个样本的距离，取其最小值并记为()。根据式（4）计算每个样本点被选中的概率（为样本数），并不断计算聚类中心与每个样本点的距离，直至个中心选取完成。接下来的步骤与原始-means算法相同。

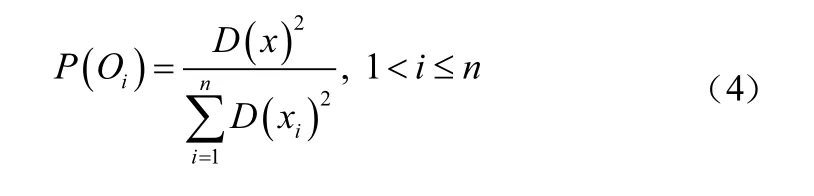
2 模型实现

对于用户用电行为分析，其整个模型功能的实现主要分为以下五步：第一步，导入必要的模块，从数据库文件中读取历史电力负荷数据；第二步，进行数据清洗，即查询当前数据中的空缺值，并把空缺值删除；第三步，为更好地避免用电行为的差异，过滤掉周末的用电数据，并将不同的时间分列；第四步，通过聚类模型完成可视化类的构建，以便对数据进行分析；第五步，调用模型得到最终结果。模块功能实现流程如图3所示。

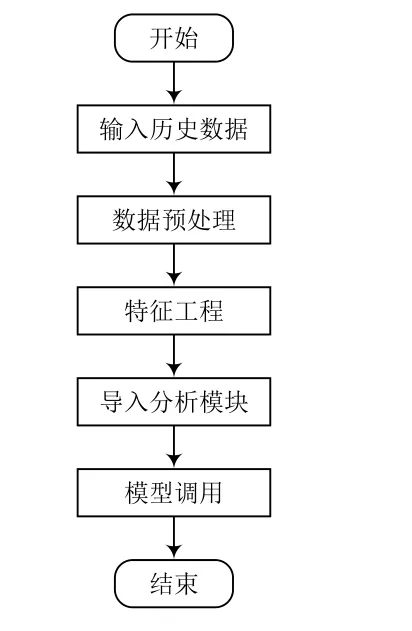
图3 模型功能实现流程

3 实验与分析

算法试验在Python3.7环境下开展，采用Python语言编写程序，数据源自某能源数据库。首先导入从数据库中下载的数据，然后进行数据清洗，即查询当前数据中的空缺值，并把空缺值删除。本文随机选取某地区2015年7月20日的电力负荷数据，该数据中共有213户用电用户。假设工作日每天的用电情况相似，过滤掉周末的用电数据，再随机选取某一天，得到一组用户用电负荷数据；导入得到的数据，得到该日不同时间不同用户的用电特征曲线，如图4所示。图中显示的结果规律性并不明显，不利于下一步的分析。因此，应对当前得到的数据进行聚类处理。

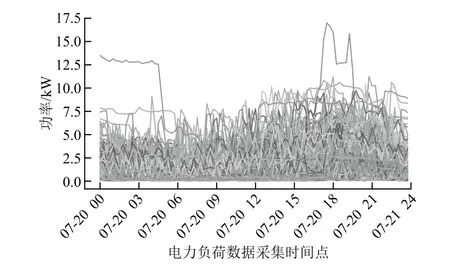
图4 用户用电特征曲线

当前数据经过聚类处理后，聚类数量与距离的关系曲线如图5所示。从图中可以看出，值增加，样本点与中心点的距离反而较小，反之则增加。

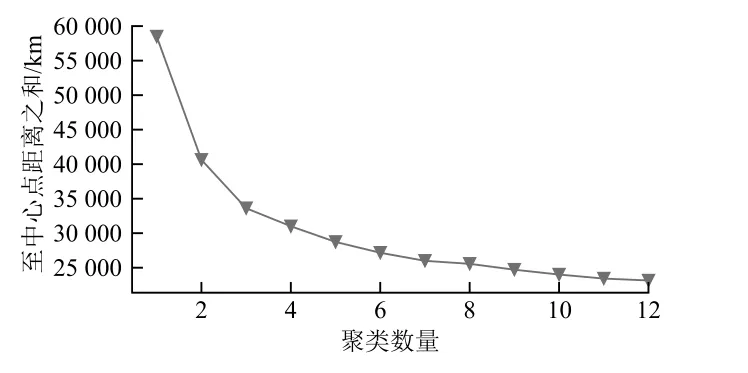
图5 聚类数量-距离关系曲线

由聚类数量-距离关系曲线可知，取值为4或5均可。本文值取5，构建了一个聚类数量为5的模型。利用模型对数据进行分组，各组用电数据曲线的对比如图6所示，图中黑色粗线为每个聚类的平均值。

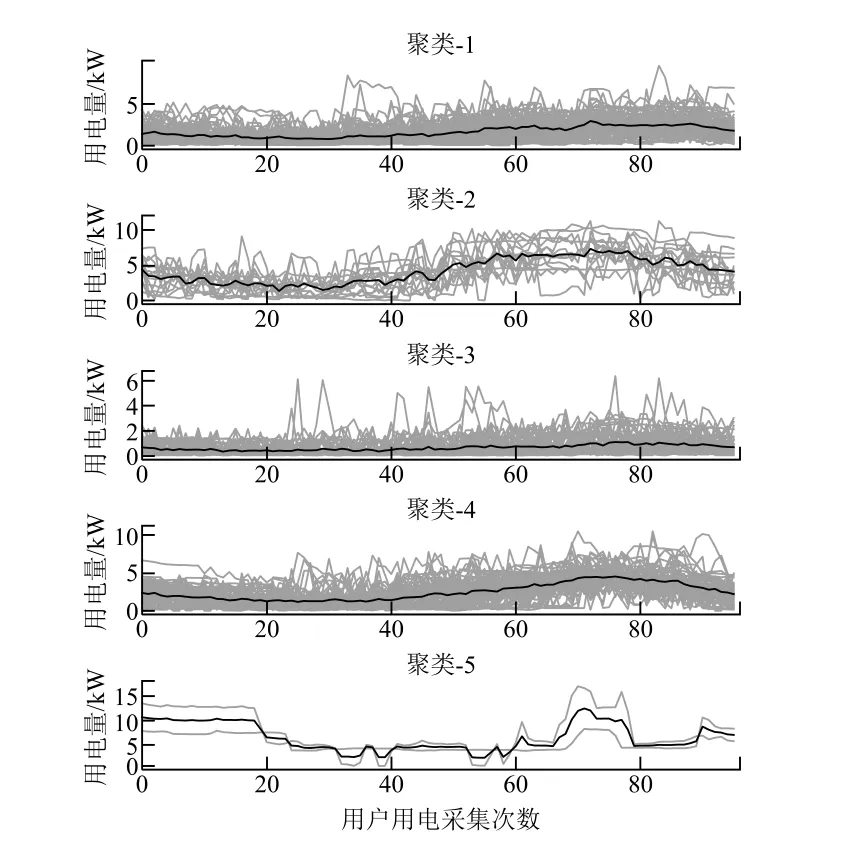
图6 数据进行5分类后的结果

为方便观察和分析，本文把5个聚类结果的平均值曲线放到一张图中进行对比，绘制出如图7所示的不同类型用户用电行为曲线。

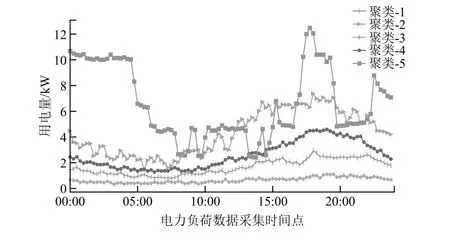
图7 不同类型用户用电行为曲线

聚类模型根据用户用电量的梯度，将213户用户分成了5类。

第1类用户的数量为77户。该类用户的用电量从10:00开始上升，18:00左右用电量达到峰值后开始逐渐下降。该类用户数量是五类用户中最多的，但其整体用电量不算大。此类用户属于供电公司的基础客户，供电公司应该保持住这类用户的用电活跃度。

第2类用户的数量为15户，数量较少。该类用户的用电量从8:00左右开始增加，且整体来看用电量较多，所以此类用户可能是某些公司或工厂。

第3类用户的数量为56户，数量较多，但其全日的用电量一直较低，且一整天波动不大。用户可能当日出门不在家或是独居的退休老人。供电公司可以考虑如何提升该类用户的用电活跃度。

第4类用户的数量为63户，用户数量较多，且其全日的用电量变化与第1类用户类似，可以与第1类用户归为一类。区别就是第4类用户的日平均用电量较高，但其也是供电公司的基础客户。从曲线可以看出，此类用户的用电峰谷平时段分界明确，供电公司可以此为依据，为其制定更加精确的供电方案和收费策略。

第5类用户的数量为2户，用户数量最少。此类用户的夜间用电量很大，用电曲线起伏也较大，考虑到晚上电价便宜，此类用户可能是某些大型生产商。

各类用户具体行为有待结合实际情况做进一步分析。

4 结 语

本文随机选取了数据库中某一天的数据进行了分析，提出了基于聚类算法的用户用电行为分析方法。经过数据预处理、聚类个数的选取，最终采用-means++算法对213户用户某工作日的日负荷曲线进行聚类，并对用户进行用电行为的分析。因大多数用户的用电行为是习惯性的，即在一周或者更长时间内，用户的电能消耗行为可能一直保持不变，故也可以按此方法确定用户一周甚至更长时间的功耗习惯和类型。此外，考虑到用户主要是夜间用户，供电公司可以考虑降低电价，鼓励用户在夜间使用更多的电力，这对电网的健康更有利。通过基于分类模式的用户日用电量分析，可以更好地了解用户的用电行为。本文针对每种类型的电力负荷展开用户用电行为分析，以方便供电公司给用户提供更合理的套餐服务；同时根据不同类型的电力消费用户，收取不同的税费，并提高系统的电能利用效率，为今后的工作提供可靠的依据。