开关磁阻电机的分数阶终端滑模控制
2022-03-15高洁王华宇徐萌
高洁, 王华宇, 徐萌
(中国民航大学 电子信息与自动化学院,天津 300300)
0 引 言
开关磁阻电机(switched reluctance motor, SRM)具有结构简单,能适应恶劣环境,容错率强等显著优势。但是由于SRM自身的强非线性,很难建立精确的数学模型,当电机的内部参数变化时,传统的PID算法难以满足系统对高性能指标的要求。随着控制理论的发展,迭代学习控制、内模控制、滑模控制等诸多算法相继应用于SRM调速系统,其中滑模控制具有较强的鲁棒性、对模型精确度要求不高,能够很好地适应SRM转速控制系统,然而常规滑模控制中系统的快速性和抖振程度是相互矛盾的,并且只能得到系统状态的渐近收敛特性。
针对滑模控制的抖振问题,许多学者给出了解决方案,例如将模糊控制[1-2]、神经网络算法[3-4]、边界层[5-6]与滑模控制结合。文献[7]针对一类非线性欠驱动系统设计了一种改进的二阶滑模控制方法,该方法可以保证控制输入及其导数的平滑性,进而成功避免了抖振问题,将该方法应用于桥式起重机系统,得到了很好的控制效果。文献[8]首次提出了分数阶鲁棒控制的概念并将其应用在汽车工业中,可以看成分数阶微积分里程碑式的应用成果。文献[9]采用分数阶积分滑模面和自适应趋近律,即使系统存在不确定项,也能获得较高的收敛精确度,仿真结果表明分数阶滑模面的抖振情况确实优于整数阶滑模面,该控制方法具有较高的跟踪精确度和鲁棒性。文献[10]针对高速直线运动球型机器人的模型设计了一种分数阶积分递阶滑模控制器,仿真结果说明该控制方法的收敛速度、稳定性、鲁棒性和抖振情况均优于普通的滑模控制器。文献[11]将自适应分数阶微积分滑模面应用于永磁同步电机调速系统,利用李雅普诺夫定理证明了系统的稳定性,对比了整数阶控制器与分数阶控制器的控制性能,证明了分数阶控制器具有更优越的动态特性和抗干扰能力。
在收敛时间方面,传统的线性滑模面只能得到系统状态的渐近收敛特性,终端滑模控制将非线性函数引入滑模面,来实现系统的有限时间收敛。文献[12]认为传统的滑模控制只关注系统的最终状态,并没有对系统的瞬态做约束,针对该问题提出了一种有限时间有界性的滑模控制,引入系统分段策略,对到达阶段和滑模阶段的有限时间有界性分别进行了分析,通过对制导系统仿真,验证了所提方法的有效性。文献[13]针对不确定非线性系统的有限时间控制问题,提出了一种自适应滑模扰动观测器与连续非奇异终端滑模控制率结合的控制方案,并且证明了观测器误差和系统状态都是有限时间收敛的,仿真实验说明该方法提高了系统的综合控制性能。文献[14]探讨了终端滑模控制在SRM调速系统中的应用,该控制器可以使系统保持线性滑模面的收敛速度和在有限时间内收敛到平衡点,通过与PID控制器对比说明其具有更快的收敛速度。
针对目前SRM滑模控制中的抖振问题和渐近收敛问题,基于上述文献的思想,本文提出一种改进分数阶终端滑模面,保证系统的状态到达滑模面后,始终具有较快的收敛速度并可以有效改善系统的抖振。然后说明该分数阶滑模面是Mittag-Leffler稳定的,基于李雅普诺夫稳定性理论分析整个系统的稳定性和有限时间收敛特性。将该改进分数阶终端滑模控制器应用于SRM转速控制中,通过与常规滑模控制器进行对比,证明该方法的有效性。
1 分数阶微积分与有限时间收敛特性分析的预备知识
定义1:函数f(t)的Riemann-Liouville型分数阶积分的定义为[15]
(1)
式中:i>0是分数阶积分阶次;Γ(i)是Gamma函数。
给定函数的RL分数阶微分定义为
(2)
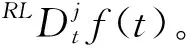
定理1:若存在连续正定V(x):Rn→R满足[16]
(3)
(4)
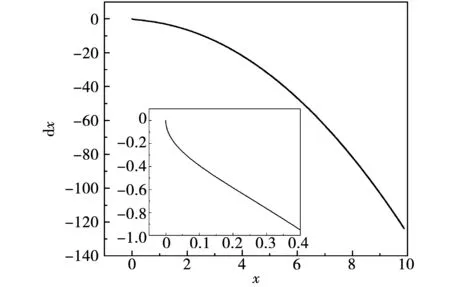
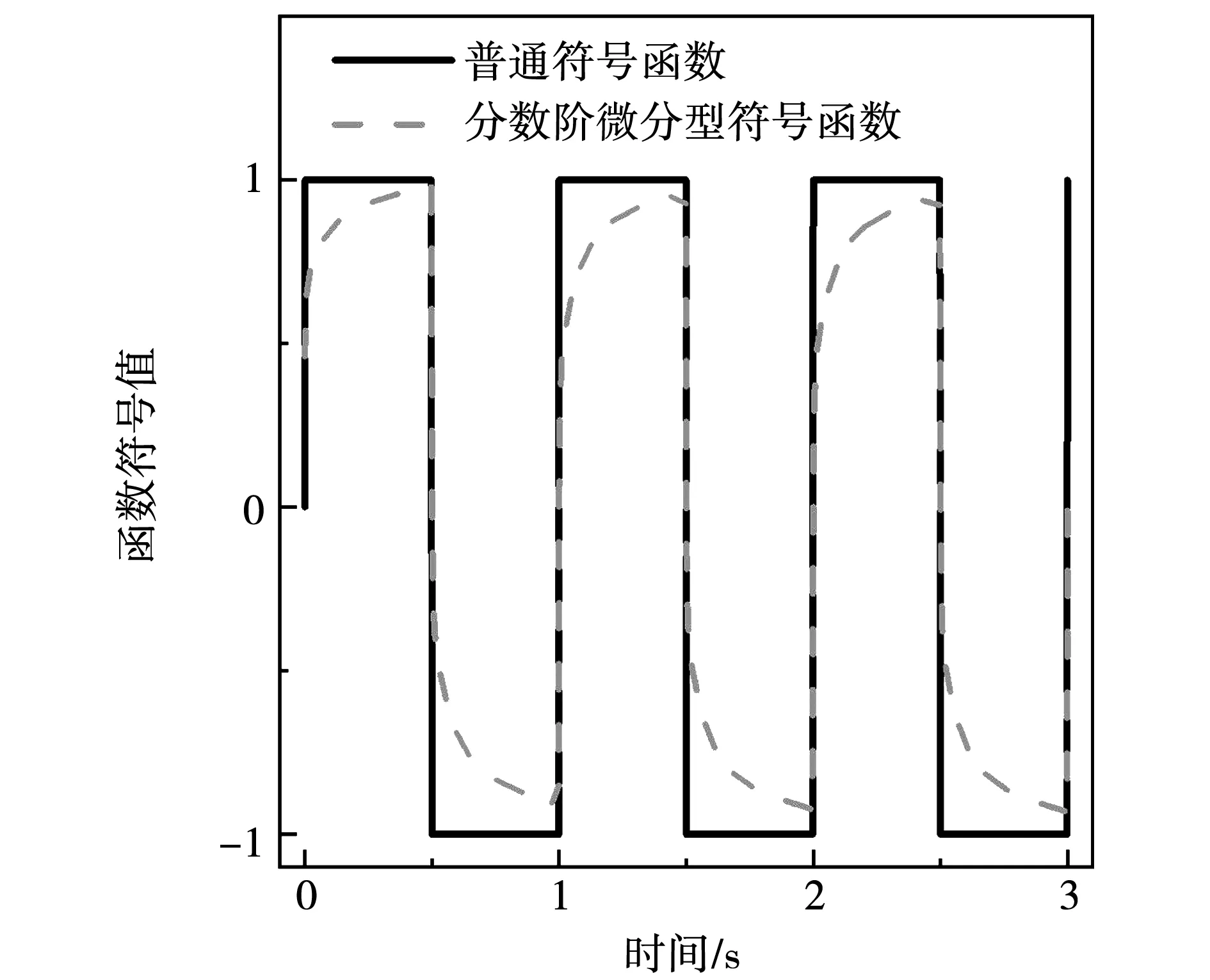
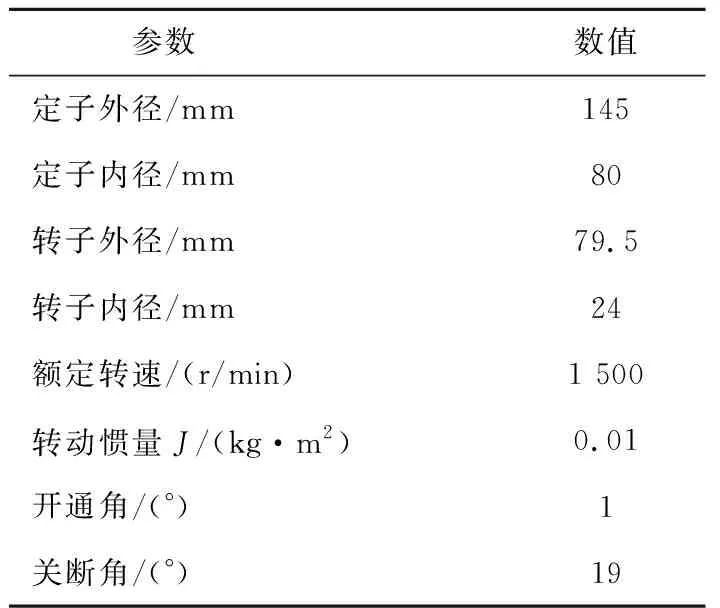
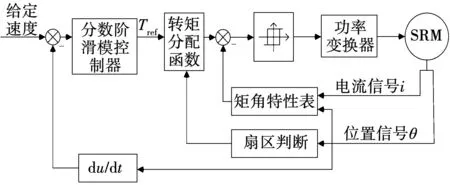
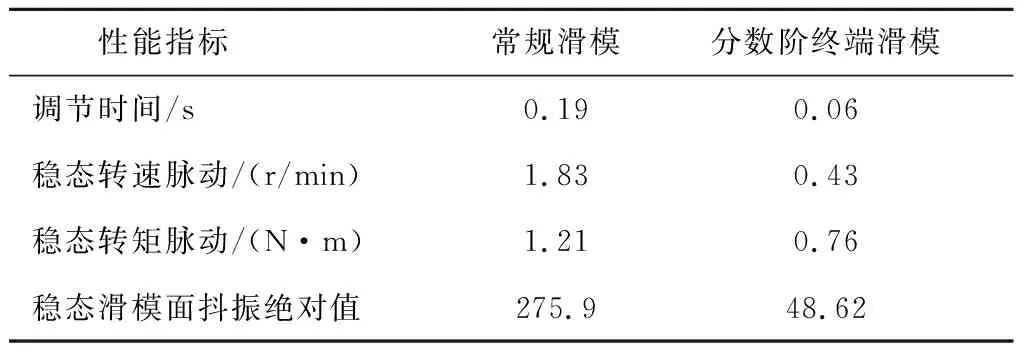
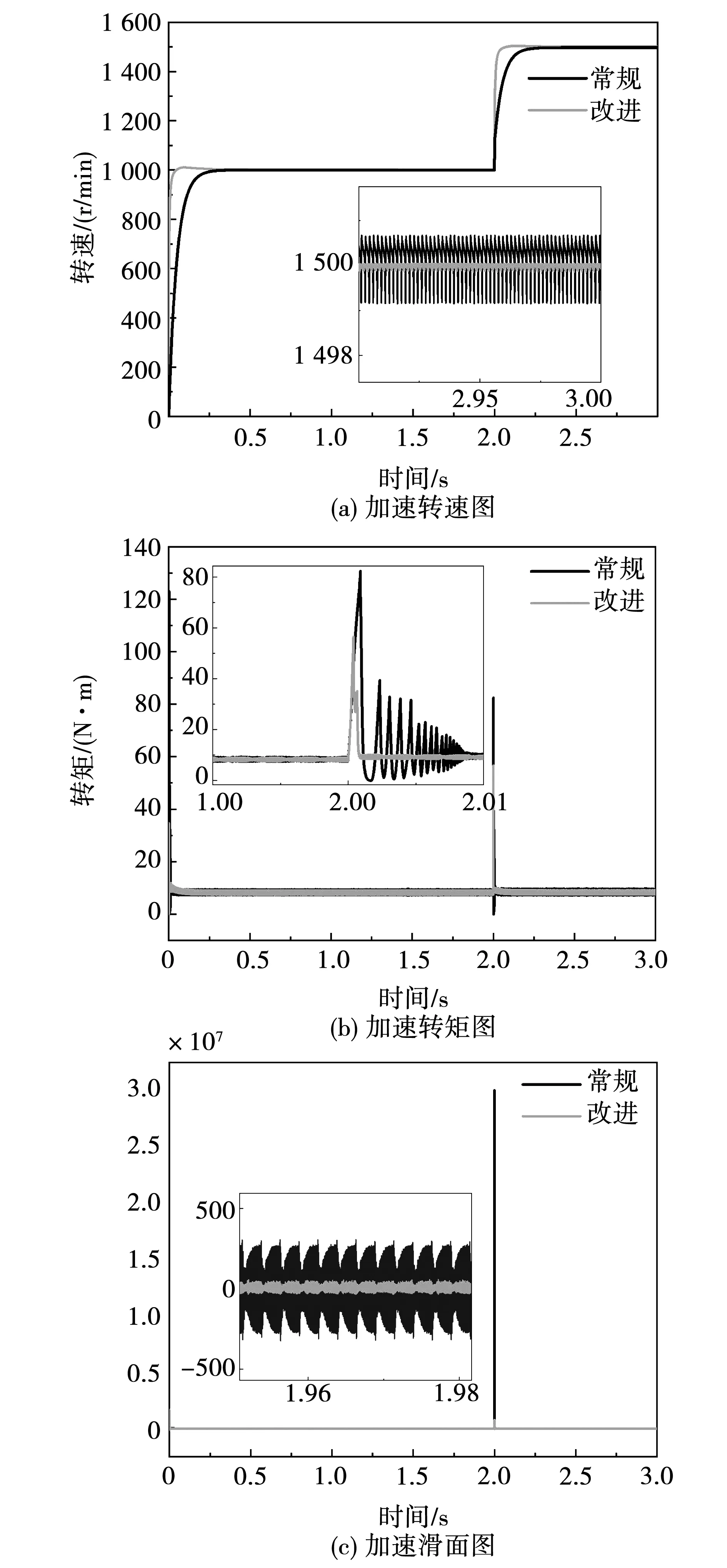
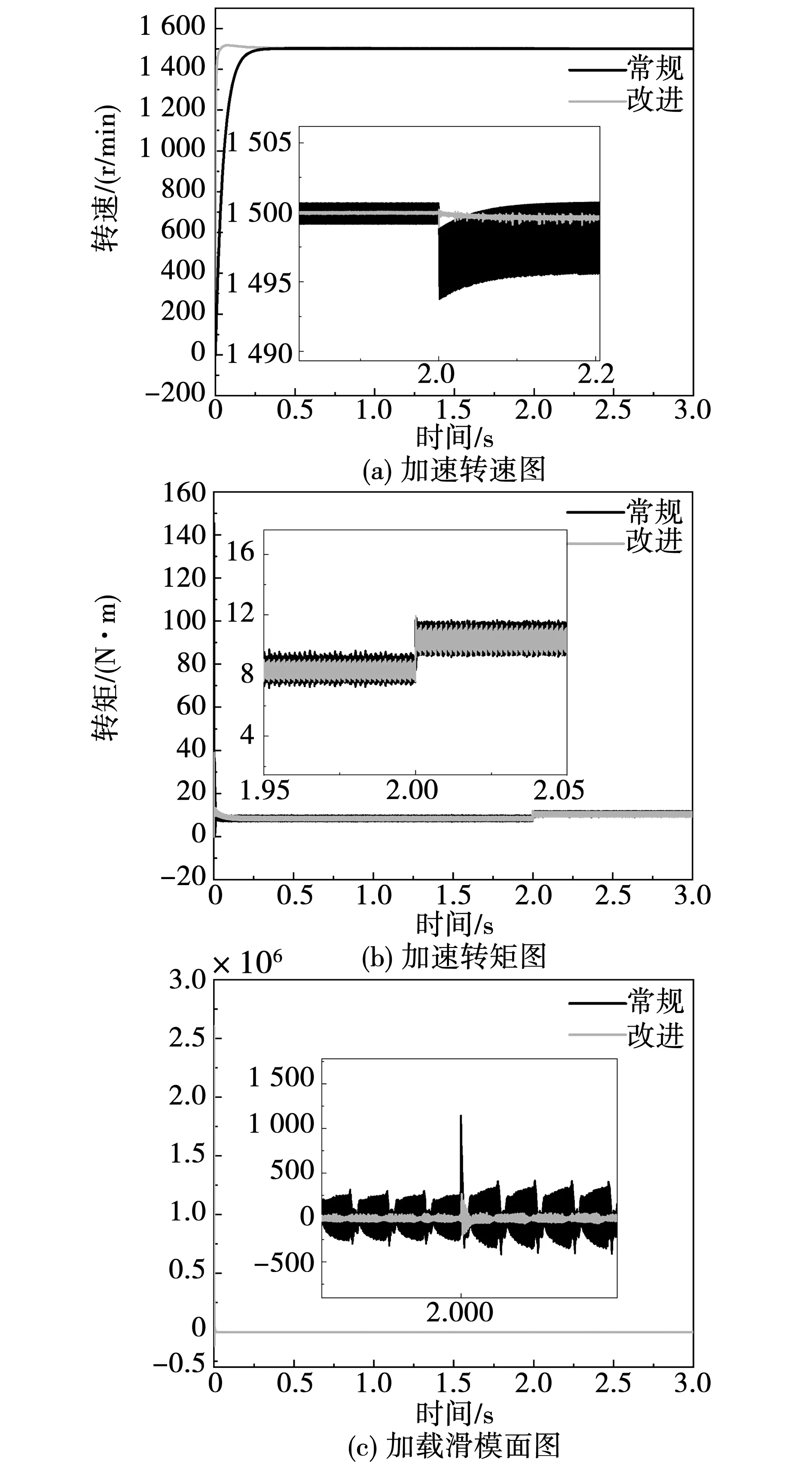
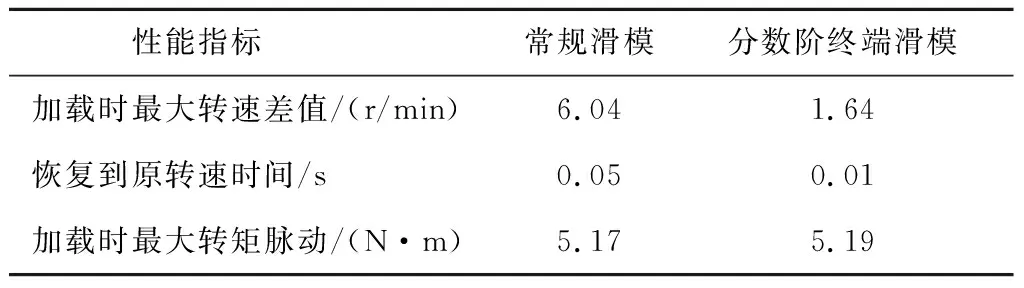
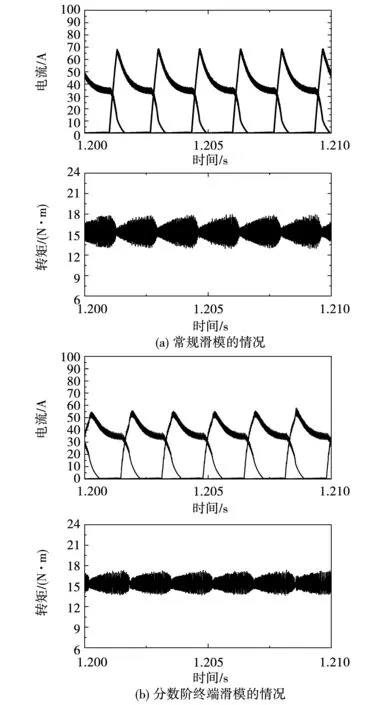
式中参数η>0,0 (5) 引理1:幂函数f(t)=tμ,且μ>-1,则[15] (6) 引理2:设Xeq=0是系统的平衡点,D⊂Rn是包括原点有界的闭域。如果函数V(t,X(t))∶[0,∞)→R关于t是连续可微的,X满足局部Lipschitz条件,并且[17] a1‖X(t)‖a≤V(t,X(t))≤a2‖X(t)‖ab, (7) (8) 式中t>0,X∈Ω,ξ∈(0,1),a1、a2、a3、a和b是给定的任意常数。那么Xeq=0是Mittag-Leffler稳定的,如果假设条件在Rn上全局成立,则Xeq=0是全局Mittag-Leffler稳定的。 由SRM的转子机械运动方程 (10) 进一步转化为状态空间表达形式 (12) 根据文献[19],得到如下的终端滑模面 (12) 式中0<α<1。此时系统的收敛情况如图1所示,可以看出当系统状态远离平衡点时,收敛速度很慢。 图1 0<α<1时的相平面图Fig.1 Phase plan of 0<α<1 提出如下改进终端滑模面 (13) 式中β>1>α>0,由图2可知该滑模面保证了x1在整个相平面都有较快的收敛速度。 图2 β>1>α>0时的相平面图Fig.2 Phase plan of β>1>α>0 文献[20]说明了分数阶滑模面减弱系统抖振的基本原理,本文将分数阶微分项引入改进终端滑模面,最后选取改进分数阶终端滑模面为 s=c1|x1|αsign(x1)+c2|x1|βsign(x1)+Dγx1。 (14) 式中c1>0,c2>0,β>1>α>0,1>γ>0。 对式(14)求一阶导数可得 (15) 则可由式(15)得到等效控制率为 (16) 取切换控制率为 usw=-D1-γ[ksign(s)]。 (17) 分数阶微积分形式的符号函数的性质与符号函数的性质类似[21],分数阶微分型符号函数和普通符号函数的对比如图3所示,其中分数阶微分的阶次为0.1,输入为正负周期变化的函数,输出为该函数的符号函数。 由图3可以看出,分数阶微分型符号函数可以降低系统状态变量在开关面附近的切换幅值,使得系统的状态更加贴近滑模面,削弱系统抖振。 图3 两种符号函数的对比Fig.3 Comparison of two sign function 改进分数阶终端滑模控制率为 u=ueq+usw。 (18) 由于在滑模面中引入了非线性项和分数阶微分项,常规李雅普诺夫函数无法分析本文提出的滑模面稳定性。下面将系统在状态空间中分为|x1|<1和|x1|≥1两部分讨论,然后先根据引理2证明所提出的改进分数阶终端滑模面的稳定性,再证明其有限时间收敛特性。 取a1=a2=1,ab=2,p为偶数,q为奇数且p、q互质,再取常数λ与p、q满足以下关系 (19) 当|x1|<1时,首先讨论引理2的第1个条件,取函数 (20) 取a、b和λ满足以下条件 (21) 从而有 a1|x1|a≤V(x1)≤a2|x1|ab。 (22) 即可证明式(7)成立。 再讨论引理2的第2个条件,当系统状态到达滑模面时,有s=0,则由式(14)可得 Dγx1=-c1|x1|αsign(x1)-c2|x1|βsign(x1)。 (23) 对式(20)求γ阶导数,由引理1可得 (24) 由式(21)中的参数取值和Γ函数的性质可得 (25) 将式(23)代入式(24)可得 (26) DγV(x1)≤0。 (27) 再由式(26)得 DγV(x1)=A(-c1|x1|α+2λ-c2|x1|β+2λ)≤ -2minA(c1,c2)|x1|α+2λ。 (28) 只需α+2λ≤2且a3为满足a3≤2min(c1,c2)的任意正常数即可满足式(8);当|x1|≥1时,再取a、b、λ和β满足以下条件 (29) 利用上述方法,可证明在|x1|≥1时满足引理2,即改进终端滑模面是Mittag-Leffler稳定的。 假设系统的可达性成立,系统的状态在切换控制率的作用下可以收敛在|s|≤Δ中。 取c3=2max(x1,x2), ||x1|δsign(x1)|=max(||x1|αsign(x1)|, ||x1|βsign(x1)|) 当D1-γ|x1|sign(x1)≠0时,式(15)可写为 (30) 只有下式成立,式(14)才能保持分数阶终端滑模面的形式,即 (31) 由式(31)可得 c3-D1-γs[D1-γ|x1|δsign(x1)]-1>0。 (32) 由引理3和式(32),令p=∞可以得到 (33) 由引理3,令p=∞可以得到 (34) 引入一个时变参数σ≥1,式(33)可写成 (35) 由式(33)和式(35)可得 (36) 从而得到 (37) 将式(37)代入式(14)得到 c2D1-γ|x1|βsign(x1)|≤ |D1-γs|+|c1D1-γ|x1|αsign(x1)|+ |c2D1-γ|x1|βsign(x1)|≤ K1Δ+|c3|x1|δsign(x1)|≤(K1+1)Δ。 (38) 当D1-γ[|x1|sign(x1)]=0,有 (39) 根据以上分析可以得到,若系统的状态s可在有限时间内收敛到|s|≤Δ,就能说明x1可在有限时间内收敛到式(37)。 为了确保系统的状态能够达到并维持在滑模面,设李雅普诺夫函数为 (40) 将式(40)求一阶导数,可得 (41) 将式(15)与式(18)代入式(41)可得 (42) 由李雅普诺夫稳定性理论可知所设计的控制率可使系统从状态空间中的任意初始位置抵达滑模面。 (43) 在Ansys中建立SRM的模型,其具体参数值如表1所示。基于Maxwell 2D对SRM的电磁特性进行求解,得到T-i-θ和ψ-i-θ数据,然后在Simulink中利用查表模块和SRM各变量间的关系,建立SRM的非线性数学模型[22]。本文以四相8/6开关磁阻电机为研究对象,以减小调节时间和转矩脉动为目标,采用改进分数阶终端滑模控制和转矩分配控制建立转速转矩双闭环控制系统。 表1 电机参数 SRM控制系统的总体框图如图4所示,外环是转速控制环,内环是转矩控制环。控制系统的转速信号通过分数阶终端滑模控制器产生转速外环的输出信号,该输出信号再作为转矩内环的预期转矩。转矩分配策略以合成输出转矩等于预期转矩为目标,分配每相转子在不同位置的期望转矩,使合成瞬时转矩跟踪上转速外环输出的期望转矩。由式(10)可以看出,系统的控制变量是电磁转矩Te。转矩分配函数为余弦转矩分配函数[23],即 图4 系统框图Fig.4 Structure of system Tref(k)=Tref×fk(θ)。 (44) 式中:θon为导通角;θoff为关断角;θov为重叠角;τr为周期;Tref(k)为第k相参考转矩;Tref为总参考转矩。 为了验证所提分数阶终端控制器的有效性,本文将比较常规滑模的控制效果与改进分数阶终端滑模的控制效果,从加速和加载两个方面对系统进行动态仿真,并分析稳定运行时的电流与转矩。取常规滑模面为 s=cnx1+x2。 (45) 趋近率为 (46) 其中常规滑模控制器的参数为cn=18、kn=800,改进分数阶终端滑模控制器的参数为c1=8、c2=15、α=0.4、β=1.5、γ=0.8、k=1 200。 在加速情况下,SRM转矩为8 N·m,转速从1 000 r/min突增到1 500 r/min,两种控制器的仿真波形如图5所示。其中黑色为常规的滑模控制器,灰色为改进分数阶终端滑模控制器。 两种控制器在加速时的具体数据如表2。 表2 加速情况下不同控制方式性能对比 图5(a)、表2可以说明改进分数阶终端滑模控制系统可以更快地跟踪上给定的转速,并且系统稳定后转速的波动更小,改进的分数阶终端滑模面提高了系统的动态特性。图5(b)为转矩的变化情况,在稳态情况下,转矩脉动减小了30%左右;当系统的给定转速发生改变时,转矩也会相应的变化,因为设置转速升高,由系统框图可知给定的转矩也会增加,转速稳定后,转矩重新回到原始值,故转矩会出现先升高后降低的趋势。当时间间隔足够小时,SRM转矩的变化量与转速的变化量可以看作成正比。改进分数阶滑模控制器优秀的动态特性可以迅速使系统达到给定的转速,从而减小调速过程中转矩抖动的时长和幅值。图5(c)是系统运行过程中滑模面的响应曲线,无论是升速还是稳态阶段,改进分数阶滑模面的抖动幅值都远远小于常规滑模面,说明分数阶的切换趋近率改善了系统在到达阶段的抖振情况,分数阶的滑模面改善了系统在滑动阶段的抖振。 图5 加速情况下的波形对比Fig.5 Waveform comparison under acceleration 在加载情况下,SRM转速为1 500 r/min,转矩从开始设定8 N·m,突增到10 N·m,两种控制器的仿真波形如图6所示。 图6 加载情况下的波形对比Fig.6 Waveform comparison under loading 两种控制器在加载时的具体数据如表3。 从图6(a)可以看出在转矩突增后,两种控制器均有一定的转速降落,由于滑模控制的鲁棒性强,对负载扰动不敏感,因此转速波动十分有限。通过表3可以发现分数阶终端滑模控制器加载时引起的转速脉动更小,可以抑制转速波动的影响。从图6(b)和表3可以说明改进分数阶终端滑模控制与常规滑模控制相比,转矩有较大的瞬时波动,这是由于改进滑模面动态特性更好,使系统迅速做出反应,导致系统有较大的调节幅度。在短时间的波动后,改进分数阶终端滑模控制迅速回到初始转速,普通滑模控制的转矩虽然没有发生剧烈的抖动,但是其转速的调节时间明显落后。在滑模面的抖动方面,转矩增加后,从图6(c)可看出改进分数阶终端滑模控制器的滑模面和速度抖动情况基本无变化,常规滑模控制器的抖动情况明显变得更加严重。 表3 加载情况下不同控制方式性能对比 电机转速为1 500 r/min、负载转矩为15 N·m的相电流和转矩的情况如图7所示,其中图7(a)为常规滑模控制器的仿真情况,图7(b)为改进分数阶终端滑模控制器的仿真情况。 图7 电流和转矩的波形对比Fig.7 Waveform comparison of current and torque 通过观察图7可以看出,在单相导通区两种控制器的转矩都能达到给定值,且转矩比较平稳,但二者在换相区域相电流波形与转矩脉动波形有明显差异,常规滑模控制策略下相电流的上限在68.83 A,转矩波动范围在13.27 N·m到18.31 N·m,转矩脉动率为33.63%;改进分数阶终端滑模控制策略下的相电流的上限在55.14 A,转矩波动范围在13.76 N·m到17.19 N·m,转矩脉动率为22.8%。在换相过程中,常规滑模控制相电流的峰值和转矩脉动均大于改进分数阶终端滑模控制,可见,改进分数阶终端滑模控制器在换相过程中也有着更好的控制效果。 图8为实验电流波形,图8(a)为常规滑模控制的相电流波形,图8(b)为改进分数阶终端滑模控制的相电流波形。由图中可以看出,常规滑模条件下,由于换相过程中电流出现较大的波动。经过滑模优化后,电流在换相过程中较为稳定。 本文针对具有强非线性和模型不确定性的SRM控制系统研究了一种改进分数阶终端滑模控制方法: 1)设计了一种在整个状态空间中都有着较快收敛速度的分数阶终端滑模面,给出了SRM控制系统的改进分数阶终端滑模控制器的形式; 2)针对本文设计的控制器,对其稳定性、可达性以及有限时间收敛性给出了证明,从理论上说明控制器的合理性; 3)本文提出控制器使SRM系统有较好的动态特性和较小的稳态抖振,将系统的调节时间减小了68.4%,稳态转矩脉动降低了37.1%,在加速和加载的情况下,使SRM系统保持较好的运行状态,且在换相过程中改善了转矩和电流的波动情况。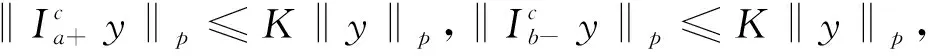
2 改进分数阶终端滑模控制器的设计
2.1 分数阶终端滑模控制器设计
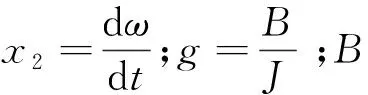
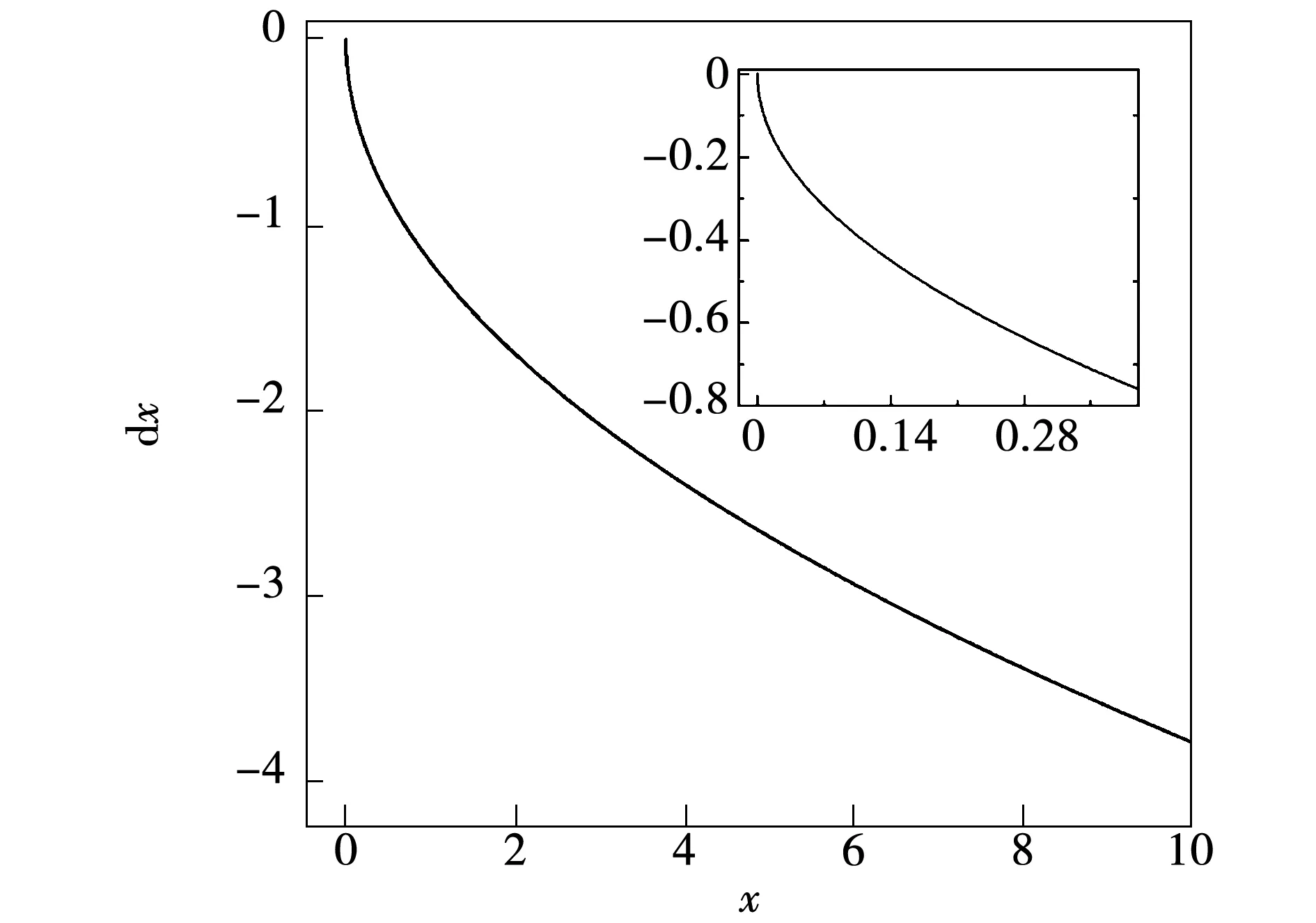
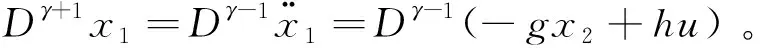
2.2 滑模面稳定性分析
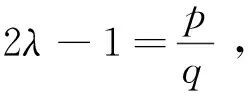
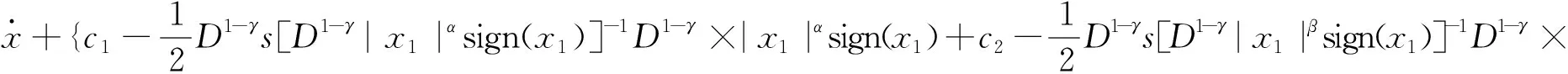
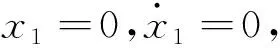
2.3 滑模面可达性分析
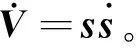
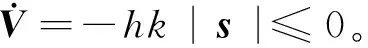
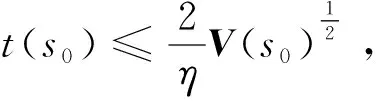
3 仿真研究与实验分析
4 结 论
