圆锥滚子主轴承热结构数值分析*

王岳峰，姜宏伟，宁文钢

(太原重工股份有限公司 技术中心，山西 太原 030024)

0 引言

风电主轴承是兆瓦级风电机组的核心部件，由于其长期在重载、变转速、交变载荷和振动等复杂工况下工作及现场检修维护极为困难，因此主轴承的稳定可靠对风电机组的正常运行起到至关重要的作用[1]。主轴承的设计及应用应考虑载荷、计算方法、选型、布置、材料、成本、热处理、润滑、密封、安装游隙、试验和检测等相关技术问题[2-4]，运用接触力学、传热学、摩擦学和流体力学等学科理论来分析风电机组主轴承具有重要意义。胡浪等[5]研究了圆锥滚子轴承滚子大端球面半径在不同工况条件下的润滑性能。Hu等[6]研究了在点接触状态下混合润滑轴承的数值计算方法。王亚彪等[7]基于弹流理论研究了在极限工况载荷条件下的风电主轴承润滑性能。Zaretsky等[8]对滚动轴承的理论寿命进行了数值计算。华希俊等[9]对激光微织构滚动轴承表面的润滑特性和弹流动压性能进行了分析。魏效玲等[10]研究了角接触球轴承的滚动体与滚道的接触应力，分析了滚道硬化对接触应力的影响。以上文献对轴承润滑性能及接触模型的研究较多，但针对风电机组圆锥滚子轴承在安装过程中的热结构耦合分析还相对较少。本文基于采用两个单列圆锥滚子轴承的两点支撑布置结构型式，对某兆瓦级风电机组上的圆锥滚子主轴承在安装过程中的各接触表面进行Hertz接触应力、变形和温度分布数值分析。

1 轴承滚子接触模型和参数设置

以某兆瓦级风电机组两个单列圆锥滚子轴承的两点支撑布置型式中的主轴承为研究对象，轴承在工作中的布置型式如图1所示。本文研究受载荷较大的靠近轮毂侧的主轴承。

图1 风电机组主轴承布置型式

运用UG NX软件建立风电机组主轴和单列圆锥滚子轴承的三维模型并进行数值分析。主轴承装配整体三维模型如图2(a)所示，剖面结构如图2(b)所示。

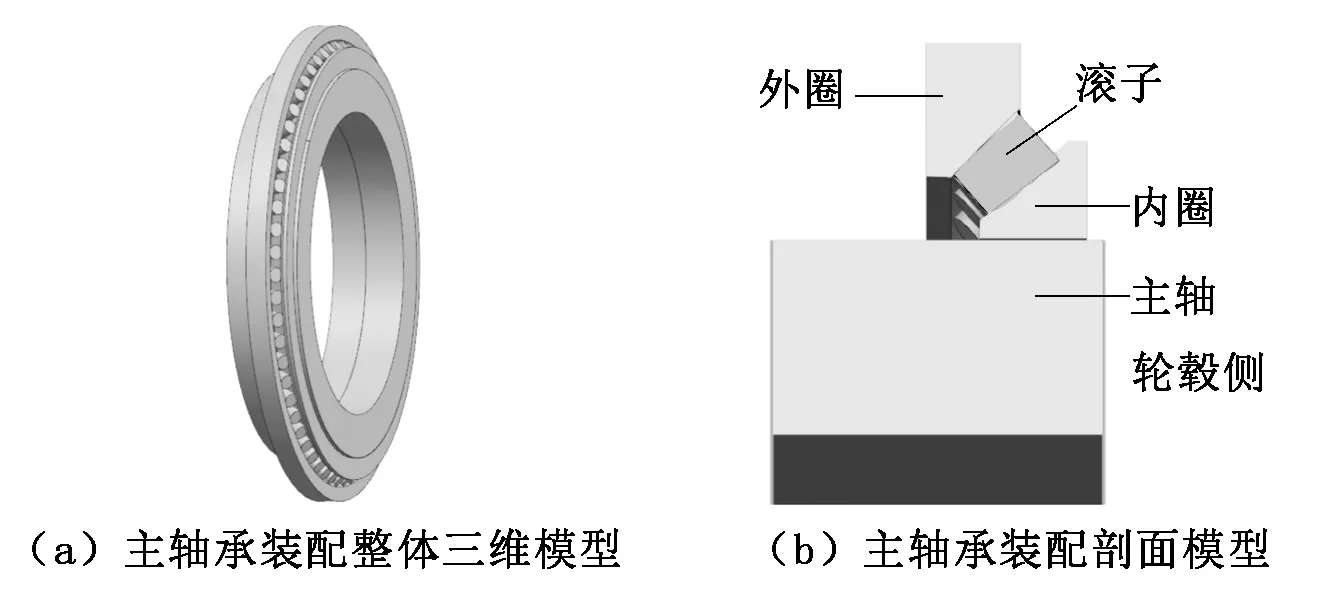
图2 风电机组主轴承装配接触模型

由于模型的几何形状呈圆周对称，所以仅取三维模型的一个滚子及部分内外滚道建立三维数值接触模型。主轴材料选取QT400-18，主轴承材料选取GCr15SiMn，轴承滚子数为85，轴承外径为2 420 mm。

QT400-18和GCr15SiMn材料性能参数见表1。

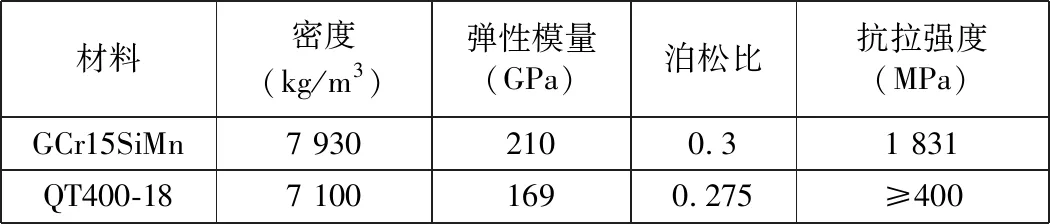
表1 材料性能参数

在分析主轴承装配和受载时，根据工况不同，在软件中设置轴承内圈与主轴的过盈量δ分别为0.5 mm、1 mm和1.5 mm；设置主轴承内圈温度分别为80 ℃和100 ℃；主轴壁厚与主轴承径向厚度比值H分别为0.9和1。

2 计算结果与讨论

2.1 接触应力、变形和温度分布

在主轴承装配过程中，先将主轴承内圈和滚子组合体与主轴过盈配合，由于滚子和内圈组合体在装配时未承受轴承外圈螺栓的轴向预紧力，因此装配分析时不考虑滚子和外圈的影响。主要分析在装配过程中轴承内圈与主轴的过盈量、主轴壁厚和内圈加热温度对轴承内圈和滚道的接触应力、变形和温度分布的影响。

图3为过盈量δ=1 mm、主轴壁厚与主轴承径向厚度比值H=1、内圈温度θ内圈=80 ℃时，主轴承内圈的接触应力、变形和温度分布云图。从图3(a)、3(b)可以看出，主轴承内圈最大接触应力和最大变形出现在内圈左侧(靠近外圈侧)，从右向左应力逐渐减小，这主要是由于主轴承内圈左侧壁厚较薄引起的。从图3(c)可以看出，主轴承内圈的温度分布为右侧(轮毂侧)温度分布梯度大，这主要是由于内圈右侧壁厚较大，在轴承内圈沿着周向朝向轴承外圈方向上，内圈单位体积传导热量较少引起的。

图3 主轴承内圈接触应力、变形和温度分布云图

2.2 过盈量的影响

图4为主轴壁厚与主轴承径向厚度比值H=1，内圈温度为80 ℃，过盈量分别为0.5 mm、1 mm和1.5 mm时，主轴承内圈内表面、内圈滚道接触面的接触应力和内圈滚道接触面变形分布曲线，其中接触起始方向为图2中的轴承外圈侧，接触终点方向为轮毂侧，图中横坐标X/L为各接触点的X坐标值与接触总长L的比值。从图4中可以看出：在δ不变情况下，当X/L增大时，接触应力略微减小，这是由于主轴承内圈厚度逐渐增大使其抵抗变形的能力变强；随着δ的增大，各接触点相应的接触应力均变大，这主要是由于过盈量增大，接触面的正压力也随之增大，接触表面的相互作用力加强。

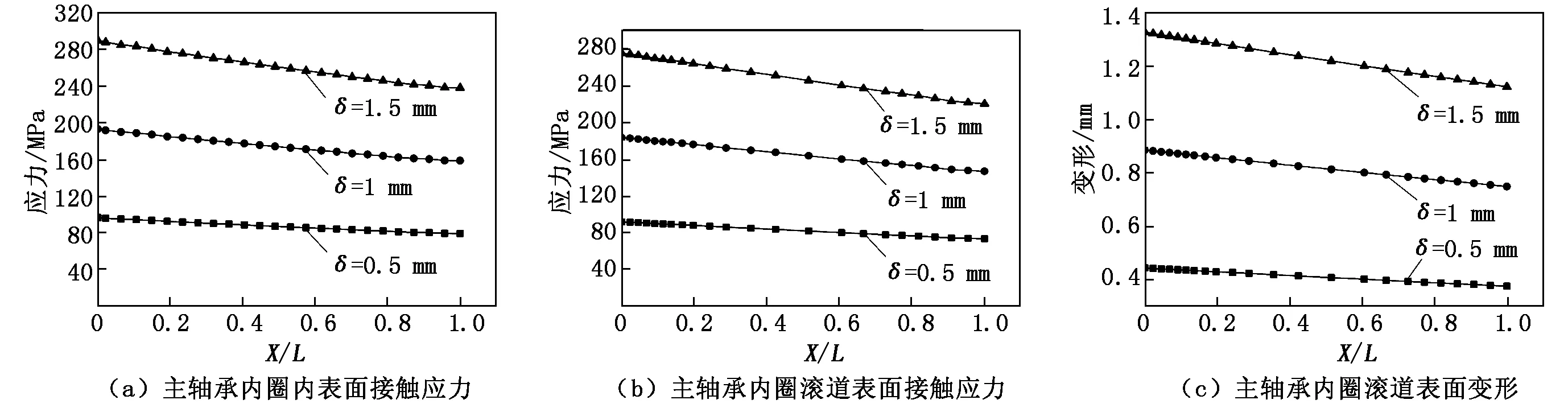
图4 不同过盈量下主轴承内圈和滚道接触应力和变形分布曲线

2.3 主轴壁厚的影响

图5为过盈量δ=1 mm，内圈温度为80 ℃，主轴壁厚与主轴承径向厚度的比值H分别为0.9和1时，主轴承内圈内表面、内圈滚道接触面的接触应力和内圈滚道接触面变形分布曲线。从图5中可以看出：在比值H一定时，随着X/L增大，主轴承内圈内表面和内圈滚道接触面接触应力和滚道变形快速减小；在接近轮毂侧，端面局部应力基本保持不变；随着比值H的增大，各接触点相应的接触应力均变小，而且应力和变形减小的梯度增大，这是由于主轴壁厚增大接触表面应力减小的原因。从图5(c)中还可以看出，主轴承内圈滚道最大变形均在0.9 mm以内，而且随着比值H的增大，接触面变形量逐渐变小，这也验证了现场装配时内圈滚道对滚子基本无影响。

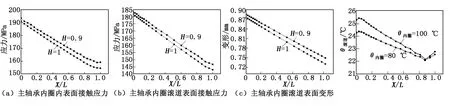
图5 不同主轴壁厚下主轴承内圈和滚道接触应力和变形分布曲线 图6 主轴承内圈滚道温度

2.4 轴承温度分布

图6为过盈量δ=1 mm，主轴壁厚与主轴承径向厚度的比值H=1，主轴承内圈温度为80 ℃和100 ℃时，主轴承内圈滚道温度分布曲线。从图6中可以看出：在主轴承内圈加热温度一定的情况下，随X/L的增大，滚道接触表面的总体温度分布为逐渐减小的趋势，但是在接触终点的挡圈附近，有局部的温度波动，这与接触表面的滚子挡边有关。随着主轴承内圈加热温度增大，内圈滚道接触表面的温度数值也逐渐增大，但其增长梯度远小于内圈的温度增长梯度，同时发现在接近X/L=1时，轴承内圈温度变化对滚道接触表面的温度基本无影响，这主要是由于轴承内圈的不同壁厚造成热量传导在滚道接触表面的非均匀分布。

3 结论

(1)主轴承内壁接触表面各接触点相应的接触应力数值，与主轴/主轴承的过盈量成正相关关系，与主轴壁厚/主轴承径向厚度的比值成反相关关系，接触应力数值的变化符合Herts弹性接触规律。

(2)在主轴承内圈加热时，靠近轮毂侧的滚道接触表面的温度逐渐减小。主轴承内圈滚道接触表面的温度增长梯度远小于内圈的温度增长梯度。