共享汽车供给模式影响下私家车用户出行方式选择演化研究

闫康礼，申栋夫，汪寒冰，牟振华

（山东建筑大学，交通工程学院，济南 250101）

0 引言

截止2020 年底，我国小汽车保有量达2.81 亿辆，取得机动车驾驶资格人数达4.56 亿人，这表明1.75 亿人没有车[1]。我国小汽车保有量居于世界领先水平，但千人汽车保有量为180 辆，距发达国家还有较大增长空间。中国拥有巨大潜在用车群体，共享汽车不失为最佳选择。欧美等发达国家共享汽车运营已经发展多年，取得了一定效果[2,3]。国内一、二线城市也成功推广，EVCARD、GoFun、摩范及Car2go 等共享汽车在北京、上海、南京、成都、济南等城市布局设点，取得了良好效果[4]。

共享汽车的租赁成本和供给模式是影响用户出行选择的两个关键因素。

租赁成本直观表现为车辆定价，Jorge等[5]拟通过定价措施控制用户出行需求，从而为共享汽车运营商创造更大的利润；Waserhole 及Jost 等[6,7]基于封闭排队网络系统对共享汽车定价进行分析，指出价格受车辆供需平衡影响；为研究协调定价措施对车辆调度和车队规模影响，Xu 等[8]将共享汽车定价模式进一步丰富；价格设置直接影响用户使用意愿，Li等[9]建立基于活动的模型分析了不同定价方案下用户对共享汽车使用需求。上述分析从不同角度反映了共享汽车租赁价格对用户选择的影响，但是没有考虑车辆供给模式的动态变化。

共享汽车分为定点式和浮动式两种供给模式：定点式共享汽车模式下（station-based car sharing），要求用户将车辆归还到运营商指定的不同停车网点，即用户在A 点取车完成自己出行以后，可以将车辆归还在运营商指定的B、C 等未达到饱和容量的停车网点；浮动式共享汽车模式下（freefloating car sharing），用户可以在合理的停车区域进行车辆的停放，包括公共停车场及合理停放点，运营商不再设置固定的共享汽车停车网点[10]。He等[11]指出浮动式和定点式供给模式的定价异同直接影响用户使用选择。浮动式共享汽车快捷方便的巨大优势吸引了公共交通使用者和小汽车使用者，研究指出约6%的共享汽车用户减少了他们私家车使用频率，浮动式共享汽车既是对定点式共享汽车的补充，两者之间也存在着较大竞争[12]。浮动式是定点式的进一步发展，两种情形下用户所考虑侧重点存在差异，参数变化也需要进一步剖析。

此外，用户出行对交通方式的选择并非静态过程，受信息不完备及价值差异等因素表现出有限理性，会根据经验效用估计不同出行方式的便捷性和成本差异[13-15]。演化博弈从动态性的角度能够对共享汽车发展情形下用户出行方式的选择机理和稳定结果进行有效分析。Bell[16,17]将博弈论首先应用于交通运输可靠性，以模拟出行时间随机性和通勤者的风险；随后，演化博弈在通勤者出行方式选择、通勤者与公共交通管理部门之间关系、交通设施最佳定价策略中进行了广泛应用[18-20]。周小祥等[21]建立共享汽车服务链联盟策略博弈，考虑了奖惩机制对稳定性的影响；肖海燕等[22,23]研究了公共交通、共享汽车和私家车之间的博弈关系，建立考虑交通管理部门和出行者策略选择的博弈模型，指出采取奖励措施同时对私家车进行管理可提高出行者出行公共交通化；卢珂等[24]针对共享汽车发展现状，从博弈角度分析了政府、运营商和用户三方的演化路径；杨倩倩等[25]基于改进的演化博弈Shapley 值分配模型探究了共享单车和共享汽车的合作分配。演化博弈为描述交通出行中决策者动态选择提供了理论基础，上述分析从不同侧面指出共享汽车发展下用户出行方式选择的复杂关系，但没有考虑共享汽车动态供给模式下用户的选择过程以及参数敏感性。

共享汽车服务过程中涉及资源供应商、用户、政府等多主体，各个主体行为的变化会对最终的策略产生影响。在共享出行盛行大环境下，共享汽车发展模式是否会改变用户现有的出行方式？不同供给模式共享汽车和私家车对用户吸引力度是如何变化的？车辆定价、数量应如何制定等问题，在研究中需要进一步深入分析。本文基于演化博弈考虑用户的有限理性，建立共享汽车两阶段供给模式下与私家车的博弈模型，分析用户出行方式选择的动态适应过程，为政策制定提供了理论支撑。

1 私家车与定点式共享汽车的演化博弈

1.1 基本假设

（1）用户群体为私家车用户，且为同一类收入群体，其单位时间成本相同[26]。

（2）博弈策略集合S={私家车，定点式共享汽车}，用户完成一次出行只能选择一种策略，并且在选择出行方式时都不知道其他个体决策[27]。

（3）博弈系统中用户总量为Φ，如果用户群体1 的数量为Φ1，用户群体2 的数量为Φ2，则Φ1+Φ2=Φ。可以将Φ2称为用户群体Φ1的对手群体，为了简化表达可称为用户和对手；反之亦成立。

（4）本文只讨论群体之间出行方式选择行为之间的演化博弈关系，在群体数量确定的情况下，一类是偏好继续选择私家车出行的用户，另一类是偏好选择共享汽车出行的用户[27]。

（5）πij表示对手选择策略j、用户选择策略i时用户的收益；同理，πji表示对手选择策略i、用户选择策略j时用户的收益(i= 1,2;j= 1,2)。

1.2 博弈模型建立

为了明确表示用户在选择定点式共享汽车和私家车过程中的成本与利益，基于相关研究[22,23,25-27]做出以下基本变量描述，如表1所示。

表1 变量定义表

通过上述假设，可得到私家车和定点式共享汽车博弈收益矩阵，如表2所示。

表2 私家车和定点式共享汽车博弈收益矩阵

其中：

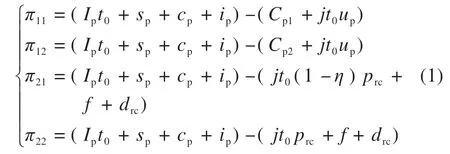
初始状态下，假设博弈系统中有比例为x(0 ≤x≤1)的用户选择私家车，故比例为1 -x的用户选择定点式共享汽车，其中x为时间t的函数。博弈过程中，随着演化进行，选择私家车和定点式共享汽车的比例都在不断发生着变化。

用户选择私家车和定点式共享汽车的理论期望收益函数分别为：

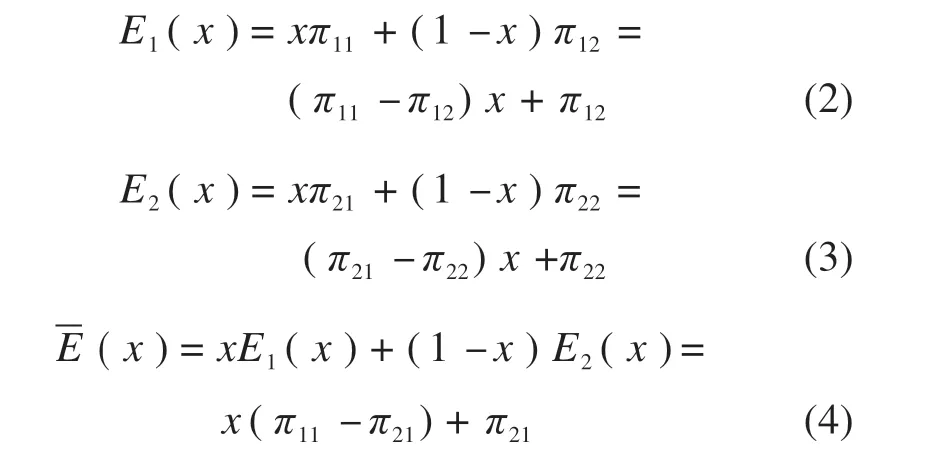
式中：E1和E2分别为用户群体选择私家车和定点式共享汽车出行时的期望收益值；-E为用户群体的平均期望收益。

1.3 演化博弈模型分析

基于演化博弈理论[28]求得复制动态微分方程如下[29,30]：

令π11-π21=M，表示对手采用私家车出行，而用户选择私家车和定点式共享汽车出行的相对收益；令π12-π22=N，表示对手采用定点式共享汽车出行时，而用户选择私家车和定点式共享汽车出行的相对收益。

（1）如果用户和对手均采用私家车出行，收益均为π11；同理，如果用户和对手都选择定点式共享汽车出行时，使用新型交通工具出行的收益也均为π22；用户选择共享汽车时不需要投入购车成本，但是定点式共享汽车便捷性、私密性等低于私家车，故第一阶段中做出假设π11>π22[26]。

（2）考虑到市场的自我调节作用，如果博弈系统中，用户Φ1选择私家车而用户Φ2选择定点式共享汽车，且此时的购车成本以及租赁价格都会小于所有用户均选择私家车或定点式共享汽车的购车成本以及租赁价格，因此，π12>π11、π21>π22。

（3）基于上述分析可以得到收益关系：π12>π11>π21>π22,因此M=π11-π21>0、N=π12-π22>0。

将局部均衡点代入上述方程组，可以得到均衡点稳定性判定，如表3所示。

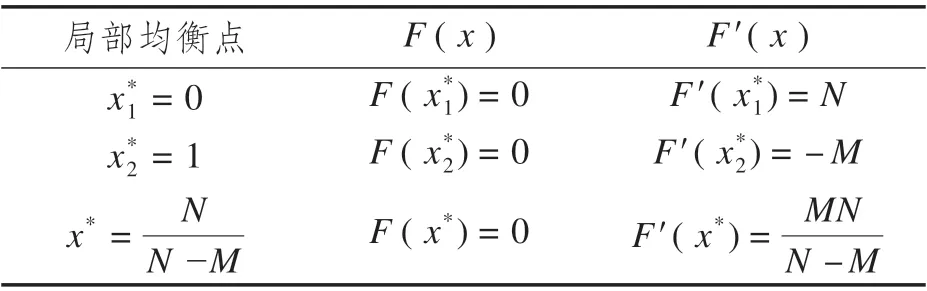
表3 均衡点稳定性判定

根据关系式（6）知道表3 中x*2= 1 是该博弈系统的唯一演化稳定策略点，即博弈主体的最终选择策略为（私家车，私家车）。

1.4 演化仿真及结果讨论

鉴于共享汽车和私家车可获取实证数据较少，通过统计分析的方法进行博弈系统演化过程较困难，同时考虑到博弈分析动态过程的独特性，本文采用数值仿真来进行模拟验证。

基本参数设定为：π11=12,π12=15,π21=9,π22=7。

（1）初始概率影响下演化路径

在演化博弈过程中，博弈主体初始选择概率会影响最终策略，也会影响系统收敛速度。为探究私家车和定点式共享汽车群体不同初始概率下策略选择过程，文章假定收益参数保持不变[22,26]，初始概率xi分别选取0.1,0.3,0.5,0.7,0.9，演化路径如图1 所示。随着用户选择私家车初始概率不断增加，系统以更缓速率收敛于稳定点1，该过程的演化周期起伏不大，迭代时间没有较大差异。这表明用户出行对私家车有较强的依赖性，定点式共享汽车作为新型交通工具，如果没有极大竞争力，最终会逐渐淡出市场。第一阶段中考虑到“经济”是用户出行关键决策因素，运营商需要对定点式共享汽车租赁价格进行优化，同时适当提高车辆基数，减少用户寻车时间成本。

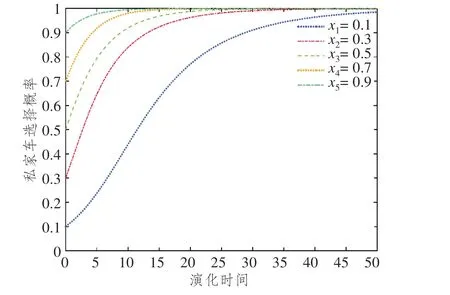
图1 不同初始概率情形下演化博弈路径

（2）初始参数影响下演化路径

图2 中所示探讨了共享汽车和私家车数量比值对稳定性的影响，其中γi为共享汽车和私家车数量比值。一方面考虑初始概率的影响，选取初始值为0.1,0.5,0.9；另一方面考虑理想情形下，共享汽车数量不断增加，γi值不断增大。明显发现，如果共享汽车数量为私家车数量的50%时，将会有20%的用户选择共享汽车；如果比值为1 时，选择共享汽车出行的用户可以达到50%；如果比值达到1.5 时，私家车出行的比例仅占20%。随着γi不断增加，用户选择私家车的速率呈陡坡式下降，并且趋于稳定点的演化周期也缩短。该过程指出共享汽车数量直接影响用户用车便捷性，主要因素是用户寻车过程中的时间损失。现阶段用户对于时间的敏感在不断提高，无法在预定时间内完成自己的出行，用户会逐渐降低选择共享汽车的意愿，因此需要合理规划共享汽车数量，满足用户出行需求从而引导用户逐渐改变出行方式。

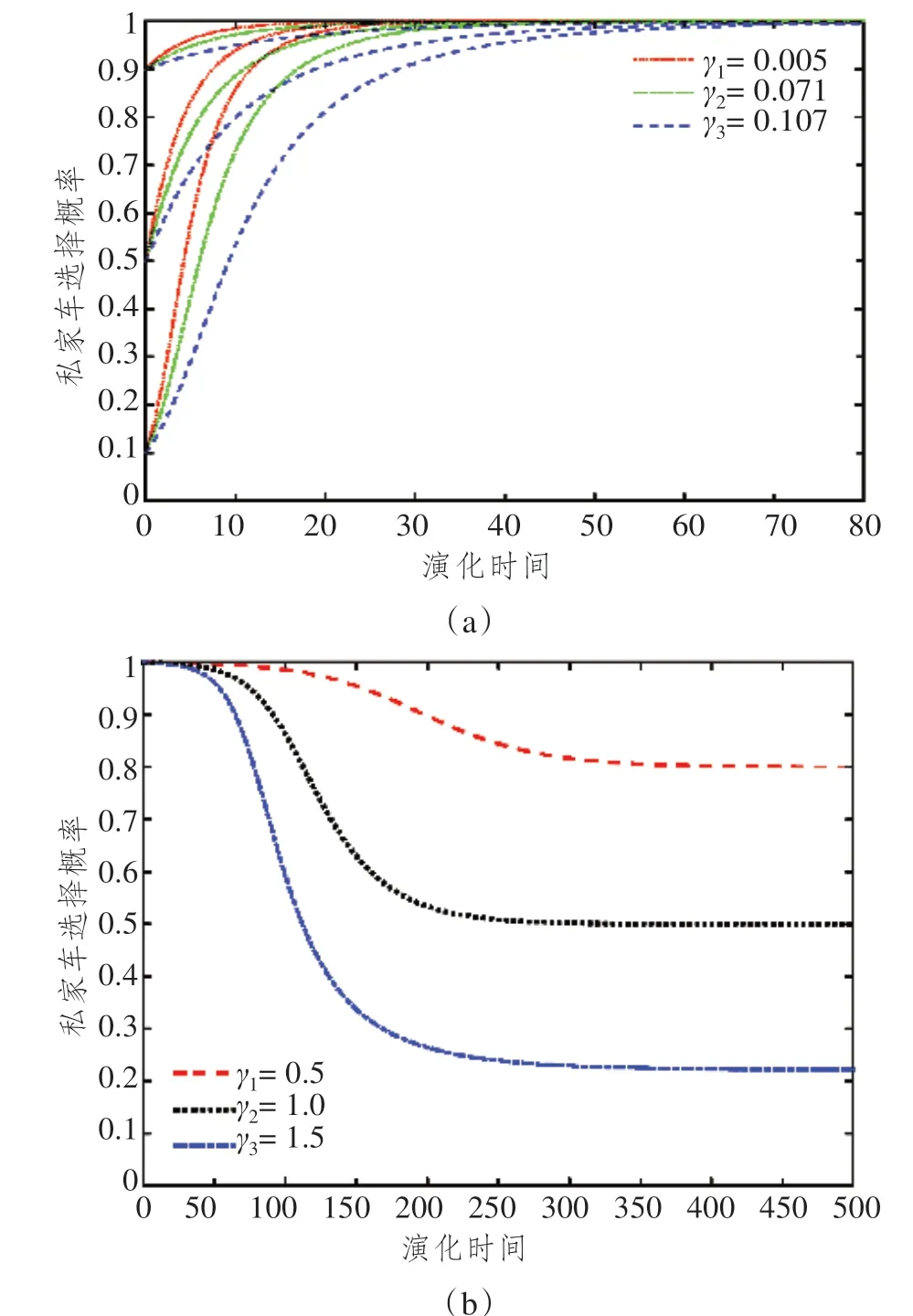
图2 共享汽车和私家车数量比值对稳定性影响

图3 分析了共享汽车和私家车单位时间花费成本比值θi对稳定性的影响，假定共享汽车使用成本为私家车的50%，此时会有10%的用户选择共享汽车；如果共享汽车使用成本为私家车的20%，将会有33%的用户选择共享汽车；当使用定点式共享汽车为用户带来的收益高于私家车时，用户会逐步放弃使用私家车，共享汽车市场也逐步扩大。该过程演化周期明显高于初始概率和数量影响，定点共享汽车处于发展初期，用车便捷性需要进一步优化，车辆定价也需要不断调整，时间成本和定价幅度是影响用户选择的两个重要因素，但是随着技术发展和市场的选择，其发展趋势是明确的。

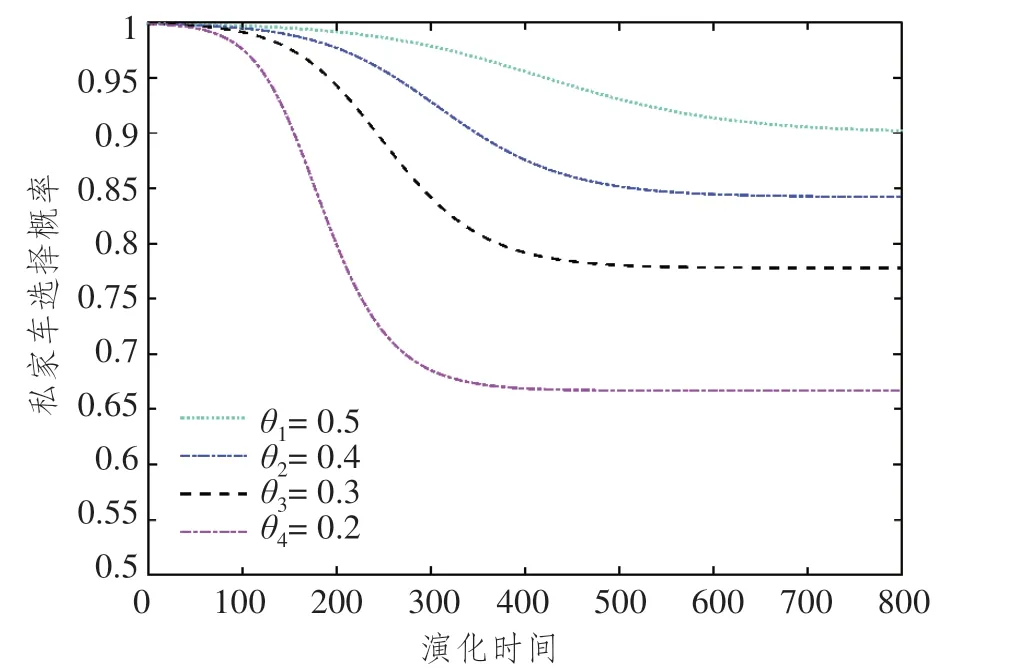
图3 共享汽车和私家车单位时间花费成本对稳定性影响

2 浮动式共享汽车与私家车的演化博弈

随着经济和科技不断发展，用户对出行需求也进一步提高，定点式共享汽车借还车的便捷性已经严重滞后。浮动式共享汽车和定点式共享汽车的最大区别在于车辆借还，浮动式共享汽车允许用户在任何合法停车位借还车，不受固定停车网点限制，提高了车辆使用灵活性。已有研究指出，浮动式共享汽车和定点式共享汽车存在竞争关系，也在逐步渗透定点式共享汽车市场[12]。因此，在共享汽车市场发展的第二阶段，建立浮动式共享汽车和私家车演化博弈模型是非常有必要的，可以把控浮动式共享汽车发展中的主要矛盾点。

2.1 模型构建与假设

以1.1节分析为基础，第二阶段用户出行可以选择的交通方式为浮动式共享汽车和私家车，即策略集合S={浮动式共享汽车，私家车}，其他假设相同。

以表1变量分析为基础，将发生变化的参数调整如表4所示。

表4 变量修正表

根据表1和表4可知，浮动式共享汽车和私家车博弈收益矩阵如表5所示。

表5 浮动式共享汽车和私家车博弈收益矩阵

其中：

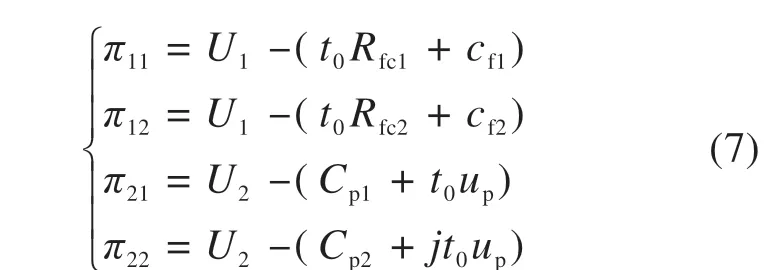
浮动式共享汽车在舒适性、私密性以及身份彰显效用方面与私家车相差无几，参数c、s、i不妨设为1，同时车辆调度费不考虑[27]，故用户使用私家车和浮动式共享汽车时所获得的位移效用近似相等，即U1=U2。式中，

初始状态下，假设博弈系统中有比例为x(0 ≤x≤1)的用户选择浮动式共享汽车，剩余比例为1 -x的用户将选择私家车，其中x为时间t的函数。随着演化不断进行，选择浮动式共享汽车和私家车用户的比例都将发生变化。

用户选择浮动式共享汽车和私家车的理论期望收益函数分别为：

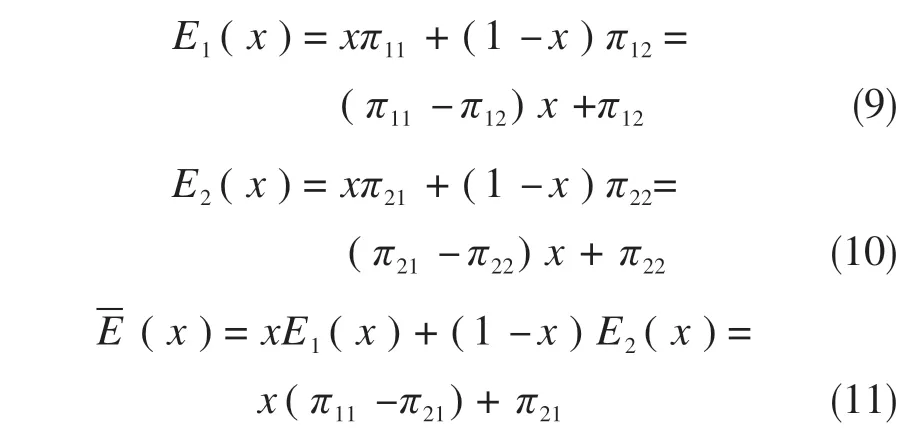
式中：E1和E2分别为用户选择浮动式共享汽车和私家车出行时期望收益值；-E为用户平均期望收益。

2.2 演化博弈模型分析

基于前面分析，可得到相同复制动态微分方程：

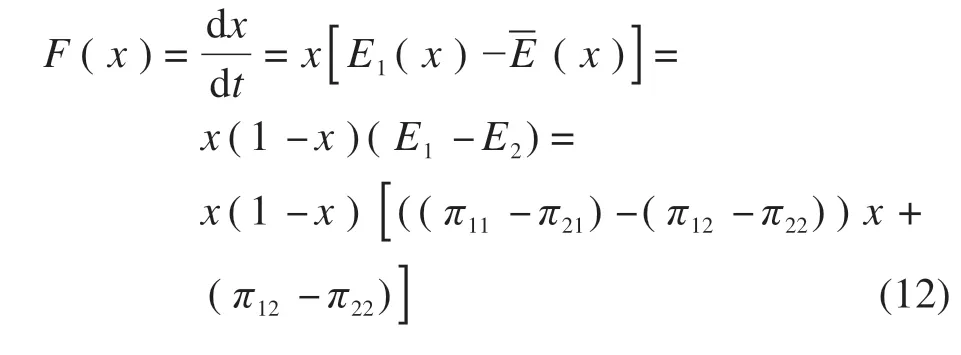
令π11-π21=M,这里表示对手采用浮动式共享汽车出行，用户选择浮动式共享汽车和私家车出行的相对收益；π12-π22=N,这里表示对手采用私家车出行时，而用户选择浮动式共享汽车和私家车出行的相对收益。

根据假设分析，可以得到：

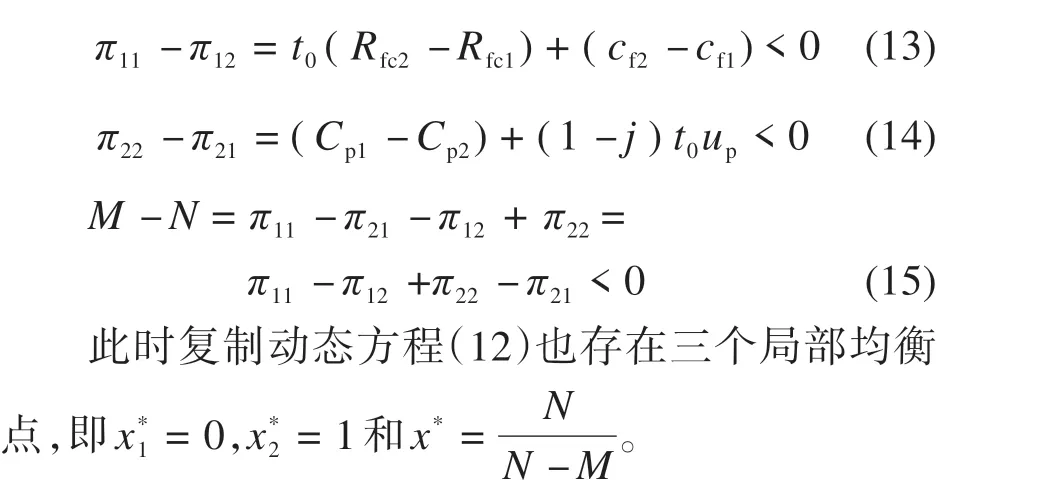
基于前面分析，可以得到表6。

表6 均衡点稳定性判定

根据ESS 判定定理，将局部均衡点代入公式（6），可知三个局部均衡点都有可能成为博弈系统的稳定点，即用户的最终策略可能为（私家车，私家车）、（共享汽车，共享汽车）或（私家车，共享汽车）。

2.3 演化仿真及结果讨论

下面首先从整体性考虑，分析收益矩阵变动对稳定的影响；其次，考虑具体成本变化对博弈系统演化路径的影响。在演化过程中仍然采用数值仿真。

（1）收益矩阵变动对稳定性的影响。收益矩阵参数取值如表7所示。

表7 不同情形下收益矩阵参数取值

首先进行初始概率对演化稳定性仿真分析，以初始数据作为基准，演化仿真如图4所示。可以明显发现，如果用户选择共享汽车的初始概率低于30%，用户会逐渐收敛于0，即选择私家车出行，由于共享汽车原始用户积累达不到一定规模，用车人数较少会降低运营商的积极性，最终共享汽车的发展将是昙花一现。随着共享汽车注册用户的不断增加以及服务质量的不断提高，将共享汽车作为出行首选的占比不断升高，仿真表明用户会缓慢地收敛于1，即选择共享汽车出行。该仿真表明在共享汽车发展过程中，原始用户的积累是至关重要的，只有当共享汽车月活跃用户达到一定规模时，才能保证运营商盈利。运营商通过不断优化服务，吸引用户选择共享汽车出行，该过程中优惠措施以及用车便捷性是运营商首要考虑的。

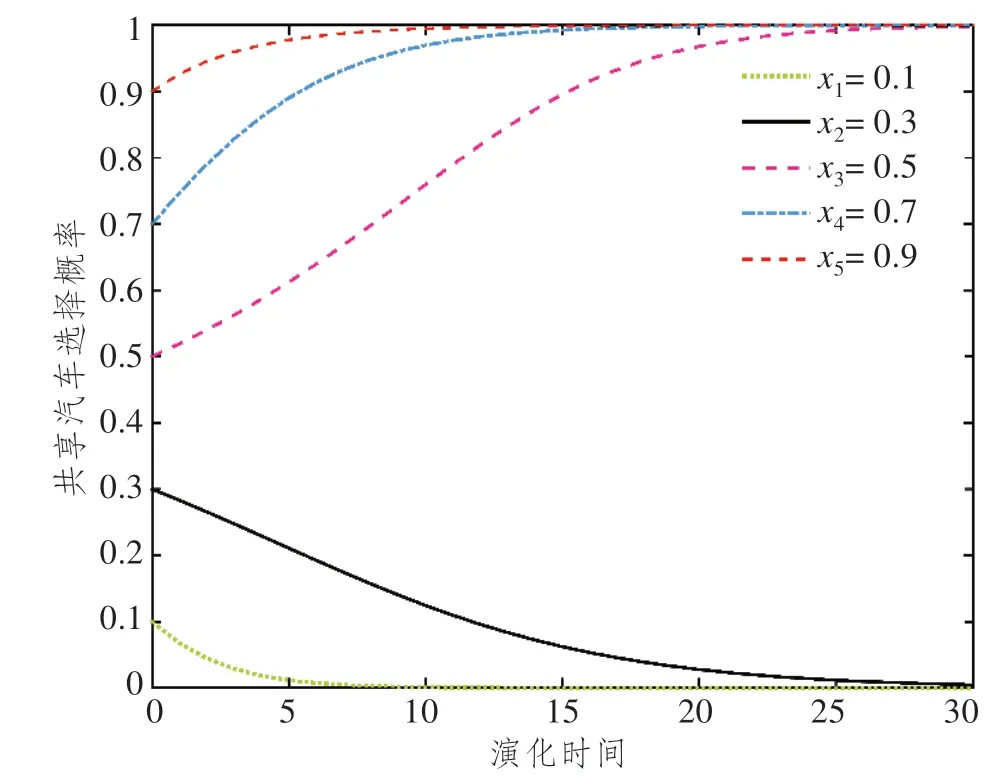
图4 不同初始概率情形下演化博弈路径

其次，考虑收益函数发生变化时系统的演化路径，如图5～图8所示。

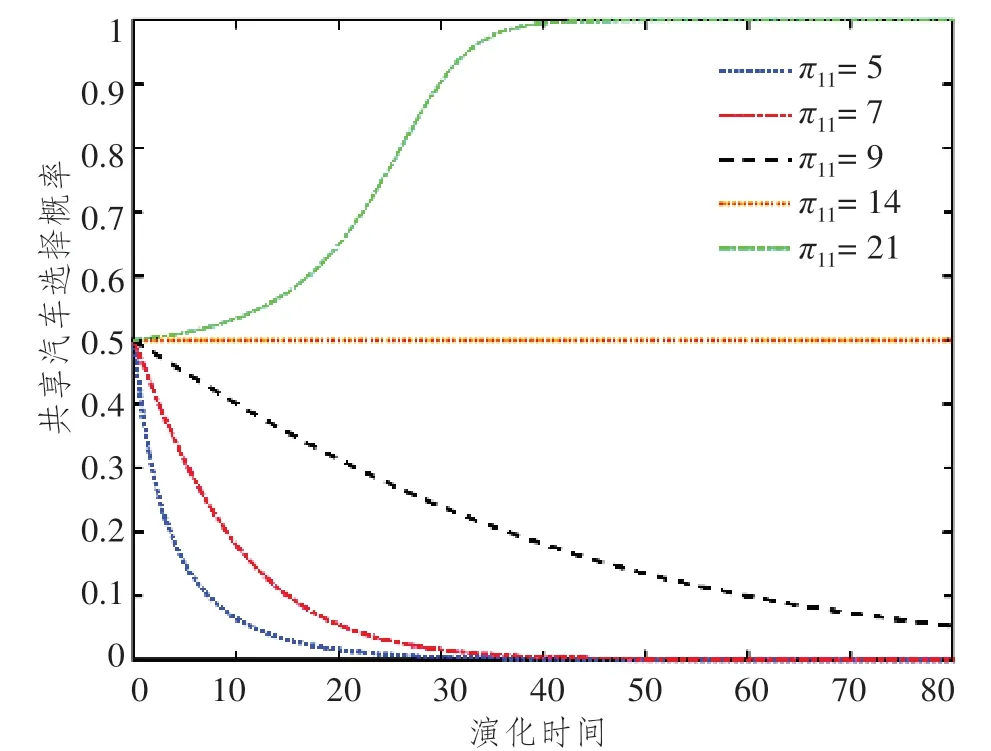
图5 用户均选择浮动式共享汽车出行时收益π11变动下演化博弈路径

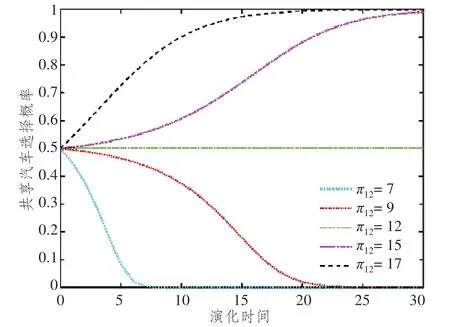
图6 部分用户选择浮动式共享汽车时收益π12变动下演化博弈路径

图7 部分用户选择私家车时收益π21变动下演化博弈路径

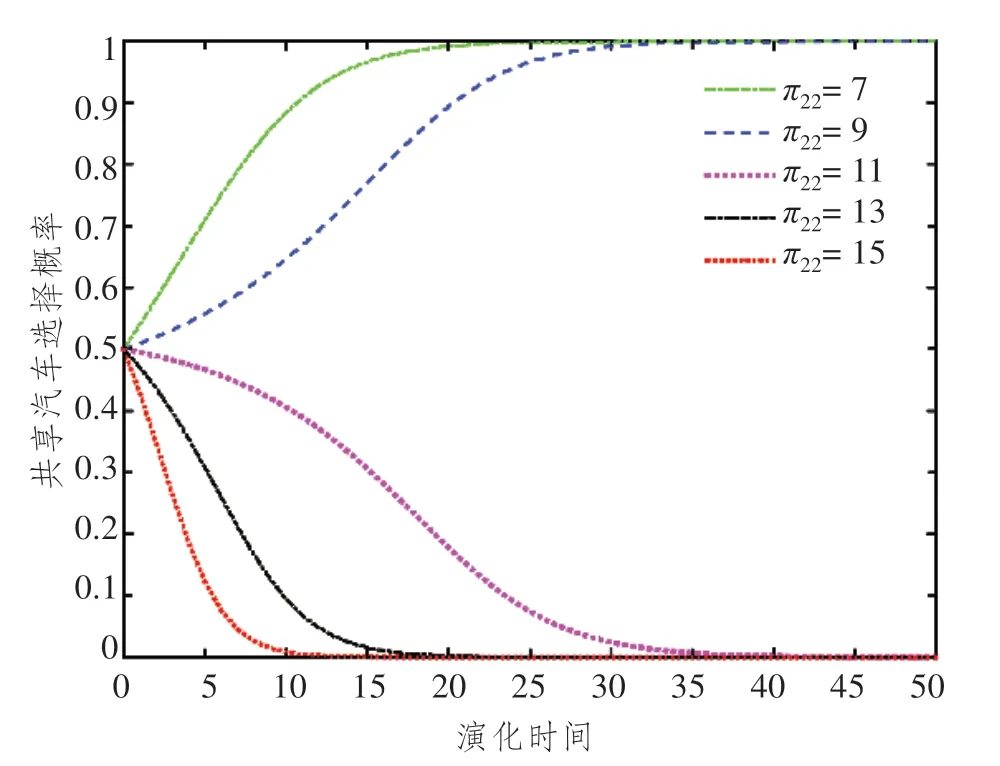
图8 用户均选择私家车出行时收益π22变动下演化博弈路径

π11表示博弈双方均选择浮动式共享汽车出行时的收益，图5 指出随着收益不断增大，用户会缓慢稳定于点1，即选择浮动式共享汽车出行；通过与初始数据对比，发现如果共享汽车出行收益为私家车出行收益2 倍时，会有50%用户选择共享汽车出行。π12表示对手选择私家车用户选择浮动式共享汽车时用户的收益，仿真图6 指出随着收益的不断增大，选择浮动式共享汽车是系统的稳定点。与原始数据对比分析可知，如果两种交通工具带来的收益相同时，用户以较快的速度收敛于0，即选择私家车出行。在仿真图7 中，π21表示对手选择浮动式共享汽车用户选择私家车时用户的收益，随着用户收益增大，博弈系统以较快的速度收敛于0，即选择私家车出行；通过与基础数据对比，可得到与图6 相似的结论，一旦私家车出行收益高于共享汽车收益，用户会迅速选择私家车，并且私家车对收益的变动更为敏感。在仿真图8 中，π22表示博弈主体均选择私家车出行时的收益，随着收益不断增大，用户会以较快的速度稳定于点0，即选择私家车出行；通过与基础对比可以发现，如果π22高于π21时，用户同样的会以较快的速率收敛于0。

上述仿真表明，共享汽车收益的增加会减缓私家车收敛于1 的速率，甚至破坏现有的稳定点，可以预见的是共享汽车的推广降低了私家车的使用。

（2）寻车成本和租赁价格两种情形进行分析

对比分析图9 和图10 可知，用户策略选择发生变化的成本价值均为0.4，但是租赁价格演化周期明显高于时间成本演化周期，这也进一步验证了在第二阶段“高效”是策略选择的主要影响因素，即供给数量影响大于租赁价格。这符合实际出行过程，随着经济水平提高，用户单位时间价值不断提高，因此用户对于时间的要求会越来越高，这表明浮动式共享汽车代替定点式共享汽车是共享汽车发展的必然过程，但是该演化周期明显变长。

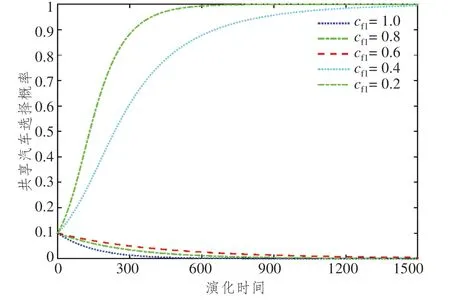
图9 寻找浮动式共享汽车时间成本cf1变化时用户选择演化路径

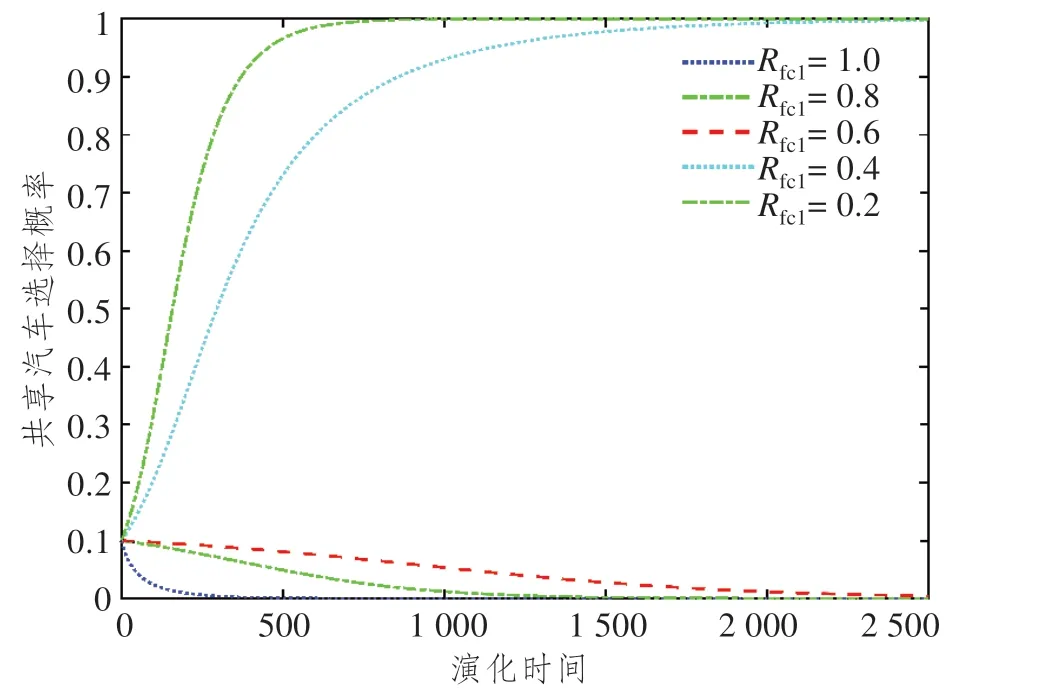
图10 浮动式共享汽车租赁价格Rfc1变化时用户选择演化路径

3 结论

本文将共享汽车不同供给模式下用户出行方式选择划分为两个时间阶段：共享汽车发展初期，影响用户选择的首要因素是租赁价格，此时建立私家车和定点式共享汽车博弈模型；第二阶段考虑用户对时间成本的高要求，取还车便捷性成为关键因素，此时建立浮动式共享汽车和私家车博弈模型。对两种情况下的博弈模型进行仿真模拟，通过对两种不同共享汽车供给模式下用户出行方式选择进行的分析，可以为共享汽车的发展提供以下结论：

（1）第一阶段中，私家车和定点式共享汽车共存是最终理想演化效果，此时定点式共享汽车数量和成本为私家车的50%。共享汽车发展不是一蹴而就，如果初期无法提供足够数量的车辆供用户使用，无车可用会阻碍用户继续选择共享汽车。

（2）第二阶段中，浮动式共享汽车发展到一定时期可以取代私家车，该过程依赖于较高的经济发展水平。此时寻找共享汽车成本和车辆租赁价格是影响用户方式选择的主要驱动力，也是政府治理的切入点。浮动式共享汽车更加体现车辆的便捷性，运营商公司要设置合理的调度方案，保证共享汽车数量的同时也要使车辆供需平衡。

（3）降低租赁价格、增加共享汽车数量等措施可以降低私家车使用频率，甚至打破现有稳定点；政府部门对共享汽车用户建立合理的奖励机制，如发放优惠券；同时对私家车出行实行一定的惩罚措施，比如提高停车成本，奖励和惩罚共同作用下可以有效促进用户出行选择共享汽车。本文探究了共享汽车供给模式影响下私家车用户出行方式选择的演化博弈过程，研究选择的博弈主体为私家车群体，对于无车群体的相关博弈过程，有待在下一步研究中进行探讨。