基于潜在类别模型的出行决策机理异质性研究
2022-03-15潘晓锋
潘晓锋,左 志
(1.武汉理工大学,智能交通系统研究中心,武汉 430063;2.辽宁对外经贸学院,信息管理学院,大连 116052)
0 引 言
在出行行为分析领域,离散选择模型一直扮演着非常重要的角色。传统的离散选择模型是基于随机效用最大化准则构建的[1]。该准则假设,每一个出行选项都会在出行者的大脑中形成一个“效用”的概念,出行者在面对一次出行选择时会选择效用最大的选项。效用是选项在出行者大脑中的整体反映或感知。由于一些不确定因素,研究者无法完整地表征出行者对出行选项感知的效用,因此,随机效用最大化准则假设出行选项的效用由确定项和随机项两部分组成。确定项表征研究者可捕捉的信息(通常采用线性加和的公式表示),随机项表征研究者无法捕捉的信息。基于对随机项不同的分布假设,可得到不同形式的离散选择模型。应用最广泛的模型是logit 模型,该模型假设不同出行选项的效用随机项服从独立且相同的标准Gumbel分布[1,2]。
在实践领域,如出行方式选择[3,4]、出行路径选择[5,6]、出行目的地选择[7,8]、私家车保有[9]、停车场选择[10,11]等场景,基于随机效用最大化准则的离散选择模型(尤其是logit 模型)得到了广泛的应用。然而,随着越来越多的研究者投入到对模型理论的研究之中,传统离散选择模型的基础——随机效用最大化准则受到了挑战。Simon提出了“有限理性”的概念[12]。该理论认为,由于信息的不完整以及处理信息能力的限制,决策者倾向于选择令他感到满意的选项,而不是选择效用最大的选项——这样会节省做决策判断的精力。Loomes和Sugden 提出了后悔理论[13],而基于后悔理论Chorus 等提出了随机后悔最小化准则,进而构建了一系列基于随机后悔最小化准则的离散选择模型[14-16]。该准则认为,为避免做完决策后出现后悔,决策者在做决策时会两两对比各个选项的优劣,进而选择最不容易产生后悔(即后悔最小化)的选项。该假设一经提出便受到了关注,陆续有研究者致力于该类模型的研究[17,18],目前俨然成为随机效用最大化准则的最有力竞争者。其他理论或准则还包括:相对效用最大化准则[19]、相对优势最大化准则[20,21]、前景理论[22,23]、自由效用模型[24]等。
从这些研究中不难得到启发,决策者的行为决策是经过复杂的信息收集、处理、评估、判断等一系列过程之后的结果。用单一一个准则或者理论去表征不同决策者的行为决策机理显然不合适,甚至用单一一个准则或者理论去表征同一决策者不同时期或不同情景下的行为决策机理同样有失妥当。因此,本研究拟考虑两种行为决策准则(即随机效用最大化准则和相对优势最大化准则①由于数据和文章篇幅限制,本研究无法将以上列举的决策机理全部纳入研究范围,仅以随机效用最大化准则和相对优势最大化准则说明出行决策机理异质性存在的极其重要性。),通过潜在类别模型结合两种行为决策准则用以研究出行者行为决策机理的异质性。
本研究的目的是验证出行决策异质性的存在,并说明忽略其存在可能带来的影响。本研究的贡献主要有以下两个方面。第一,本研究采用基于相对优势最大化准则的模型来表征出行选择行为。虽然相较于随机后悔最小化准则,相对优势最大化准则在当前的出行行为分析研究中较为少见,但是在二项选择情景下基于随机后悔最小化准则的离散选择模型和基于随机效用最大化的离散选择模型在数学上是等价的[25]。而基于相对优势最大化准则的模型却不存在这个问题。因此从这个角度来讲,相对优势最大化准则有着比随机后悔最小化准则更加广泛的应用场景。第二,本研究采用潜在类别模型分析出行决策机理的异质性。虽然出行者的异质性并不是一个新颖的课题,但是现有的研究多数集中在对出行者偏好异质性的研究上[26,27],针对出行者决策机理的异质性的研究则显得少了很多。然而,针对出行者决策机理的假设是模型构建的基础,故针对出行者决策机理的异质性研究显得尤为重要。
1 模型架构
1.1 基于随机效用最大化准则的logit模型
如前文所述,随机效用最大化准则(Random Utility Maximization,RUM)认为,从研究者的角度而言,在出行者脑海中形成的出行选项的效用可以分为确定项和随机项两部分,用数学公式表示如下:

从上式可以看出,出行者n对于第j个出行选项的选择概率只与该出行选项自身属性有关,而与选择集中其他出行选项的属性无关。该特性通常被称为IIA 特性(Independent from Irrelevant Alternatives)[1]。然而,该特性却与现实世界中的真实情况相违背。在很多情景下,一个选项的选择概率由于各种各样的原因(比如,选项之间存在相关性)会受到其他选项的影响。基于这个问题,研究者构建了基于随机效用最大化准则的其他替代模型(如probit模型、分层logit模型、混合logit模型等)或者其他的行为决策机理。
1.2 基于相对优势最大化准则的logit模型
近年来,基于随机后悔最小化准则的离散选择模型受到了广泛关注。虽然该类模型也突破了IIA 特性的限制,然而已有研究表明在二项选择情景下基于后悔最小化准则的离散选择模型在数学上等价于基于随机效用最大化准则的模型[25]。因此,在二项选择情景下,无法采用基于随机后悔最小化准则的模型来取代基于随机效用最大化准则的模型。基于相对优势最大化准则(Relative Advantage Maximization,RAM)的模型提供了另一种可能的方法[20,21]。
相对优势最大化准则认为出行选项在出行者大脑中映射的效用,不仅包括选项自身的属性,还包括不同选项之间的相对优势,用数学公式可表示如下:

式中:Ank(j,j′)表示出行者n脑海中映射的选项j对选项j′在属性k上的直接优势;Dnk(j,j′)表示出行者n脑海中映射的选项j对选项j′在属性k上的直接劣势。
借鉴随机后悔最小化准则中后悔值的定义[13],Ank(j,j′)和Dnk(j,j′)可由下述公式表示:

类似于基于随机效用最大化准则的logit 模型,假设随机项εnj服从尺寸参数为0、位置参数为1的Gumbel 分布,则基于相对优势最大化准则的logit模型选择概率可以表示为:


从上式可以看出,出行者n对于第j个出行选项的选择概率不仅与该出行选项自身属性有关,还与选择集中其他出行选项的属性相关(即相对优势)。需要注意的是,基于相对优势最大化准则的logit模型和基于随机效用最大化准则的logit模型的差别并不在参数意义的不同或者参数个数的多少。从公式(4)可以看出,基于相对优势最大化准则的logit 模型是在传统的效用函数中增加了被称为“相对优势”的部分。
1.3 结合随机效用最大化和相对优势最大化准则的潜在类别模型
越来越多的研究表明,出行者在做决策时可能会采用不同的策略。可能的情形是,某一种决策机理只能表征出行群体中某一类人的决策过程。因此,可采用潜在类别模型将出行者分类,不同类别的出行者适用不同的出行决策机理。潜在类别模型假设样本之内存在多个“潜在类别”,不同类别的出行者存在某一方面(如选择偏好、决策机理)的差异,而同一类别之间的出行者不存在异质性。在现有文献研究中,潜在类别模型被视为混合logit 模型(mixed logit model)的替代者,用以描述出行者选择偏好的异质性[9,11]。
本研究综合考虑随机效用最大化准则和相对优势最大化准则,因此将样本共分为两个潜在类别,定义为“随机效用”类别和“相对优势”类别。潜在类别模型的数学表达可采用如下形式:式中:α为待估常数。值得注意的是,可以将出行者的个人社会经济属性引入上述公式中,本研究对此不做考虑,故此省略。

1.4 极大似然估计求解模型
无论是基于随机效用最大化准则的logit 模型,还是基于相对优势最大化准则的logit 模型,亦或是两者结合的潜在类别模型,均可由极大似然估计方法求解。结合两种准则的潜在类别模型的似然函数可由下式表示:
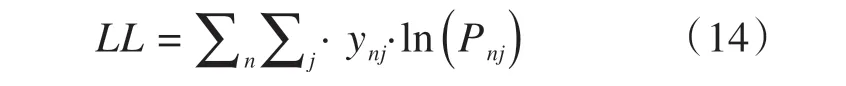
式中:ynj为哑元变量,当出行者n选择出行选项j时,ynj= 1,否则ynj= 0。
2 数据收集
2.1 SP实验设计
本研究所用数据来自基于SP实验设计的在线问卷调查。具体而言,被调查者需在给定的出行场景中选择他认为最优的选项——即高速路或者省(国)道。高速路或者省(国)道由一系列属性对其进行描述,包括出行距离、出行时间、综合费用、拥堵程度。
为了设置高速路和省(国)道各属性的具体值,本研究考虑四对出行起终点,均位于新疆,分别为乌鲁木齐市至托克逊县小草湖(省(国)道距离设为150 km,高速路距离设为160 km)、乌鲁木齐市至吐鲁番市(省(国)道距离设为197 km,高速路距离设为201 km)、乌鲁木齐市至哈密市(省(国)道距离设为640 km,高速路距离设为610 km)、乌鲁木齐市至阿克苏市(省(国)道距离设为1010 km,高速路距离设为1020 km)。注意在情景题中并没有给出起终点名称,该四对起终点只用于辅助SP实验设计。省(国)道的综合费用仅包含油耗,而高速路的综合费用除了油耗还包含过路费。油耗产生的费用由百公里油耗系数根据距离换算得到,过路费由实际高速路收费得到。总而言之,在同一出行起终点的情景下,省(国)道的距离和综合费用固定,高速路的距离固定,两者的出行时间和高速路的综合费用分别由四个等级构成(由距离换算得到的时间或者费用再加上一定偏差得到)。道路的拥堵程度采用“堵塞、拥挤、畅通”三个等级。需要注意的是,本文所说的“出行时间”指设计速度下的理论出行时间。
2.2 问卷调查
为验证问卷的合理性和填写过程中可能存在的问题,本研究首先实施了小范围的预调查。根据预调查结果,删去了SP 实验设计中存在明显优势的情景题。问卷通过线上的形式进行发放,整个数据收集过程为2020 年12 月9~15 日。共收集问卷1 071 份,其中有效问卷976 份,有效率为91.13%。每位被调查者需回答16道不同的情景题,共计得到15 616条观测数据,其中选择省(国)道的观测数据5 267 条,选择高速路的观测数据10 349 条。两者在样本中的占有率分别为33.73%和66.27%,可见总体而言,多数出行者倾向于使用高速路。
3 模型参数估计与对比
本研究采用R中的maxLik包[28]对模型参数进行估计。除去属性“拥堵状况”采用效应编码(effects coding)之外,其余属性皆为连续变量。同时,将出行选项“高速路”的效用函数中的常数项固定为0,两个选项的效用函数的确定项的具体形式为:
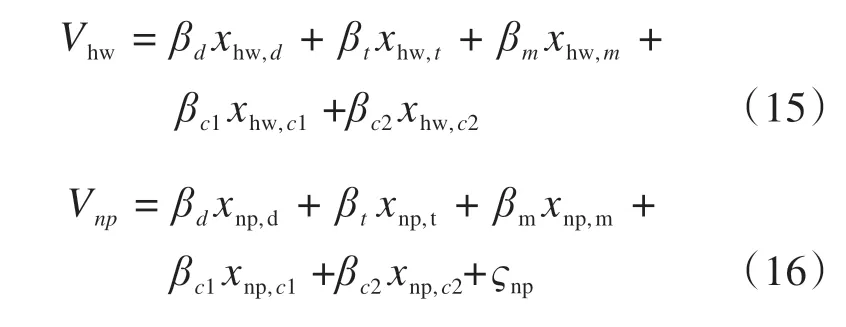
式中:下标“hw”和“np”分别代表出行选项“高速路”和“省(国)道”;下标“d”、“t”和“m”分别代表属性出行距离、出行时间和综合费用;属性“拥堵状况”为离散变量,采用效应编码:以高速路为例,当道路状况为“拥挤”时,xhw,c1= 1 且xhw,c2= 0;当道路状况为“堵塞”时,xhw,c1= 0 且xhw,c2= 1。因此,βc1用以描述“拥挤”的效用,βc2用以描述“堵塞”的效用,而“畅通”的效用则为-(βc1+βc2)。关于效应编码的详细介绍,参见文献[29]。ςnp为省(国)道效用函数的待估常数项。出行距离、出行时间和出行费用的单位分别为:km、min和元。
下面首先分别给出基于随机效用最大化和相对优势最大化准则的logit 模型参数估计结果,然后给出了结合随机效用最大化和相对优势最大化准则的潜在类别模型参数估计结果。通过对比分析,探讨出行者在做出行决策时的决策机理异质性。
3.1 基于随机效用最大化和相对优势最大化准则的logit模型参数估计
表1 列出了基于随机效用最大化和相对优势最大化准则的logit 模型参数估计结果。两个模型的ρ2分别为0.1571 和0.1572——两者均显示较好的拟合效果。同时,从模型的参数估计结果中可以发现一些结论:①在两个模型的结果中,出行距离均不显著(不显著的属性在参数估计过程中直接删除)。该结论与现有文献中相关研究是一致的[30],这表明在出行路径选择场景中(尤其是本研究的应用场景——长距离出行),出行者并不考虑距离的影响,而更多地考虑出行时间的长短。②两个模型的结果均显示,出行时间和综合费用对于出行者的路径选择呈负相关的关系,即一条道路的出行时间或综合费用越高,该道路的选择概率越低。该结论与现实情况相一致。③对于道路的拥挤状况,两个模型的结果均显示,道路的拥挤程度越低,其被出行者选择的概率越高。该结论同样与现实情况相一致。
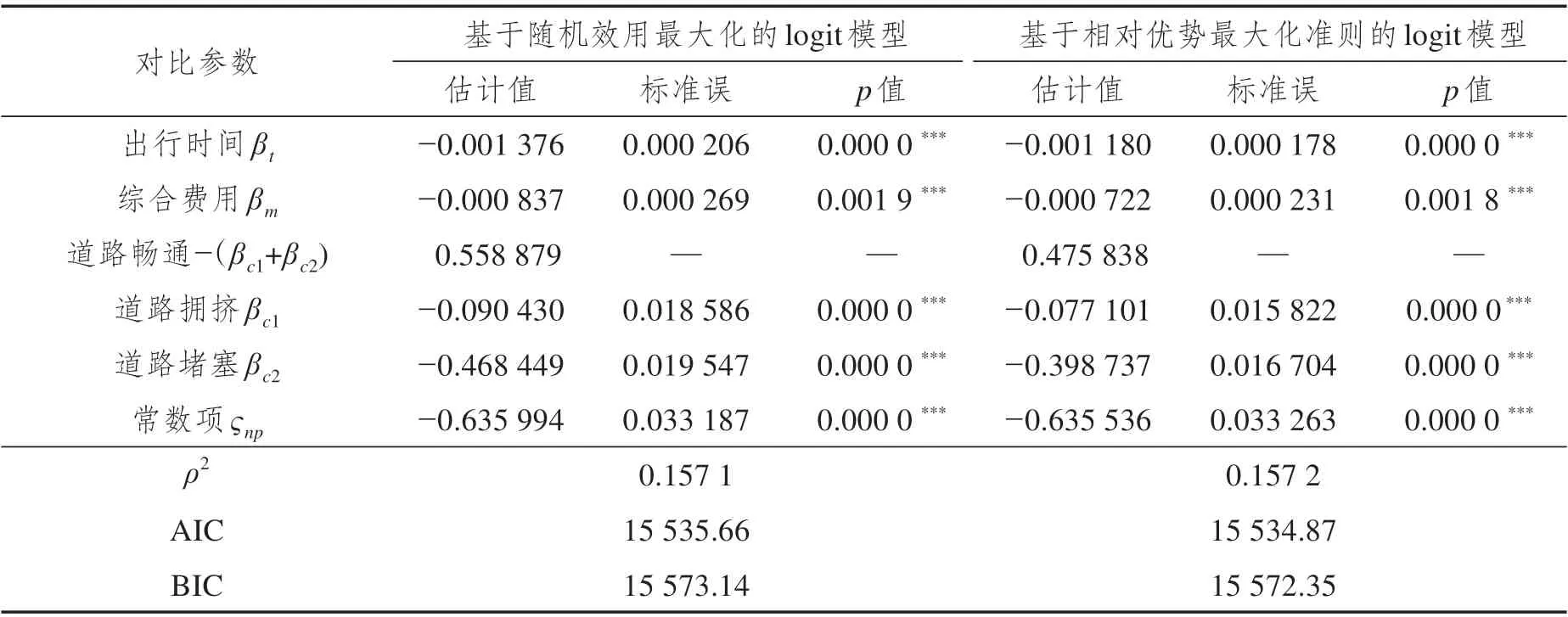
表1 基于随机效用最大化和相对优势最大化准则的logit模型参数估计
此外,本研究采用ρ2、AIC 和BIC 三个指标,对比了基于随机效用最大化和相对优势最大化准则的logit 模型的优劣。结果显示,三个指标显示两者的拟合度大致相当,基于相对优势最大化准则的logit模型略优于随机效用最大化准则的logit模型,但是该优势并不明显。仔细对比不难发现,虽然两者在拟合度上表现相当,具体参数的估计值却仍然存在差异。
3.2 结合随机效用最大化和相对优势最大化准则的潜在类别模型参数估计
表2 展示了结合随机效用最大化和相对优势最大化准则的潜在类别模型参数估计结果。需要注意的是,在两个潜在类别中只有常数项不同。如前文所述,基于相对优势最大化准则的logit 模型是在传统的效用函数中增加了该选项相对于其他选项的“相对优势”。从表2可知,该模型的ρ2为0.1604,表明该模型具有较好的拟合度。同时,由基于随机效用最大化和相对优势最大化准则的logit 模型参数估计结果中得到的结论同样适用于结合随机效用最大化和相对优势最大化准则的潜在类别模型参数估计结果。此外,表2显示潜在类别常数项估计值为-1.850 269。根据公式(12)和公式(13)可得,在所用样本中采用随机效用最大化准则做出行决策的群体约占16.58%,而采用相对优势最大化准则做出行决策的群体约占83.42%。该结论表明虽然基于随机效用最大化准则的logit 模型和基于相对优势最大化准则的logit模型的拟合度相差不大,但在所用样本中两者的分布是存在差异的。

表2 结合随机效用最大化和相对优势最大化准则的潜在类别模型参数估计
对比模型的ρ2、AIC 和BIC 三个指标,不难发现结合随机效用最大化和相对优势最大化准则的潜在类别模型明显优于其他两个采用单一决策准则的模型。该结论验证了本研究的假设,即出行者在做决策时采用的决策机理存在异质性。
3.3 基于不同模型参数估计结果的弹性分析
以上内容已经证明了出行决策机理的异质性。为了进一步说明出行决策机理异质性在出行行为分析中的重要性,下面将计算基于不同模型参数估计结果的弹性。
弹性反映某一选项的某一属性发生1%的改变对该选项或其他选项的选择概率的变化情况[29]。由于道路拥堵状况为非连续属性,本研究只考虑出行时间和综合费用的变化对省(国)道和高速路占有率的变化①由于本研究中1%的变化情况下省(国)道和高速路占有率的变化太小,故变化值设定为减少10%。。表3展示了基于不同模型结果省(国)道和高速路的出行时间和综合费用分别减少10%时各自占有率的变化情况。从中可以看出,基于随机效用最大化准则的logit 模型和基于相对优势最大化准则的logit 模型在分析出行时间和综合费用弹性时几乎没有区别,而基于结合随机效用最大化和相对优势最大化准则的潜在类别模型得到的省(国)道和高速路占有率变化值则与前两者相差较明显,尤其是当省(国)道的出行时间减少10%时,结果相差超过1%。由此可见,当忽略了出行决策机理的异质性时,可能会在后续的分析中产生误差,进而误导政策制定者做出错误的判断,最终导致政策无法达到预期目标,造成经济损失。
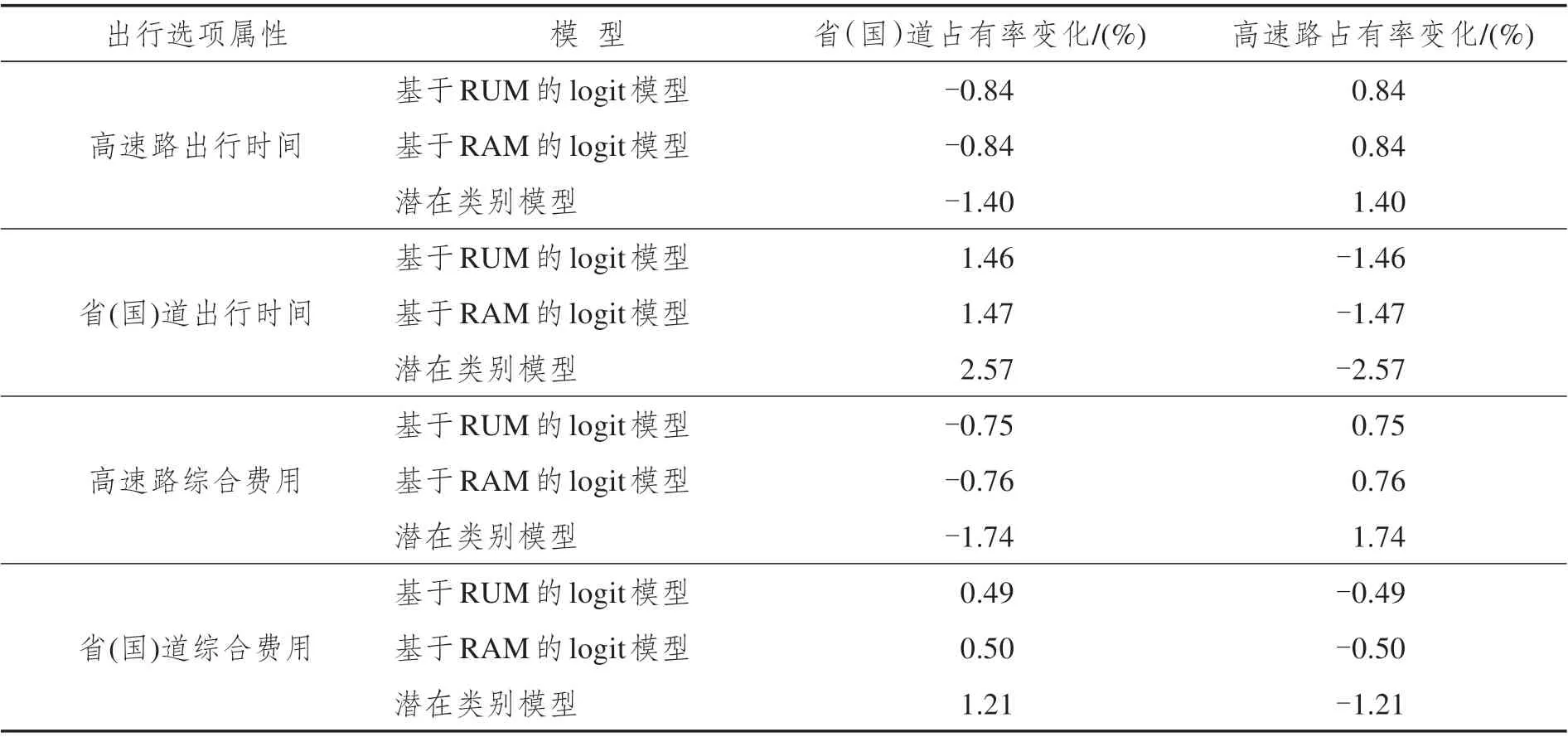
表3 属性值减少10%时出行时间和综合费用的弹性分析结果
4 结束语
本文考虑了随机效用最大化准则和相对优势最大化准则两种不同的决策机理。基于在新疆收集的关于长距离出行的道路选择意向调查数据,分别建立了基于随机效用最大化准则的logit 模型、基于相对优势最大化准则的logit 模型以及结合两者的潜在类别模型;通过对比三个模型参数估计结果与弹性分析结果,探讨了出行决策机理异质性。本研究的意义在于:借助结合随机效用最大化和相对优势最大化准则的潜在类别模型,从理论角度验证了出行决策机理异质性的存在,从实践角度指出了出行决策机理异质性的重要性。
诚然,关于出行决策机理异质性依旧有许多地方值得进一步深入研究。本研究没有考虑出行者的个人社会经济属性,只能从宏观的角度分析采用两种不同决策机理的人群的占比,而无法精确地分析两种决策机理在不同属性的出行群体中的分布。由于在二项选择情景中,基于随机后悔最小化准则的离散选择模型在数学上等价于基于随机效用最大化准则的模型,故本研究无法将其考虑在内。未来研究可以结合随机效用最大化准则、相对优势最大化准则、随机后悔最小化准则(甚至更多的决策机理)构建更加普适的决策机理异质性模型。
