基于自适应卡尔曼滤波的多传感器信号降噪
2022-03-15林旭梅石智梁
林旭梅,刘 帅,石智梁
(青岛理工大学信息与控制工程学院,山东 青岛 266520)
1 引言
我国是基础设施建设大国,钢筋混凝土腐蚀是影响建筑物结构耐久性的主要原因[1]。混凝土耐久性跟建筑物使用年限成正比,它可以保持建筑物具备长久的使用功能,维持良好的外部形态。混凝土腐蚀主要是由于内部钢筋长时间受到化学离子侵蚀、干湿循环以及外部荷载应力等因素引起的[2]。提高混凝土腐蚀检测精度,可以实时监控建筑物内部的损伤情况,避免因腐蚀造成的建筑物坍塌等恶性事故,为建筑物安全性评估和使用寿命预测等提供重要的依据[3]。
目前对于建筑物混凝土的腐蚀检测已经有了大量的研究,物理和化学方法应用较为广泛[4]。现有的数据检测结果主要集中在单传感器观测系统上,比较依赖于传感器的性能,通常不能获得足够的腐蚀特征信息,检测精度不高。多传感器数据检测系统能够克服单传感器的不确定性和局限性,提高整个观测系统的可靠性和鲁棒性。因此,本文提出了一种基于多传感器测量的检测方法,设计了动态感知综合检测系统[5]。
由于混凝土长期处在环境复杂的室外,测量传感器容易受到外部环境的干扰,在采集信号的过程中会不同程度的混有噪声信号,使得测量的信号精度偏低。针对以上问题,本文采用改进的自适应卡尔曼滤波算法[6-7],实现估计模型的动态调整,对检测数据进行实时修正。通过仿真比较,相对于常规卡尔曼滤波算法,自适应卡尔曼滤波算法降噪效果更加显著,能够提高多传感器系统数据检测的精确度。
2 多传感器综合检测系统
多传感器综合检测系统的基本结构如图1所示,它包括温度、PH传感器以及由阴阳两极组成的宏电池电路系统。

图1 多传感器综合检测系统示意图
宏电池电路系统由以下元件组成:六根单阳极棒、一根表面涂有氧化铂的钛质阴极棒、嵌入式数据采集系统、连接导线等。氯离子侵蚀作用下,阳极与阴极之间的混凝土具有了导电特性,系统能够形成导通回路。由于阴极棒表面涂有氧化铂,所以不易腐蚀、电位比较稳定,而阳极棒受到混凝土内部环境影响容易脱钝发生腐蚀。阳极棒腐蚀程度越大,电位差越大,由此可以通过观察阴阳两极之间电位差来判断钢筋腐蚀的程度。此外,当阳极棒脱钝发生腐蚀时,宏电池电路系统中的回路电流也会发生变化。所以通过测量回路中的宏电流能够判断混凝土中钢筋的腐蚀程度,宏电流越大,混凝土中钢筋腐蚀程度越大。宏电池电路系统还可以测量两个相邻阳极棒之间的交流电阻,检测电阻可以判断混凝土中两根不同阳极之间的湿度。通过以上宏电池系统实时的电压检测、电流检测和交流电阻检测,能够动态的、长期的获得混凝土中钢筋脱钝发展进程以及腐蚀的关键信息。
在钢筋腐蚀过程中,混凝土的PH是影响腐蚀变化的重要因素,同时温度的变化也会引起宏电池系统中电压、电流和电阻的变化,系统应及时获得这些参数变化信息。多传感器综合检测系统测量的数据传输至嵌入式数据采集系统,经过GPRS无线通信模块上传到服务器中,检测系统能够及时对混凝土的耐久性和安全性作出预警。
但是在使用该方法测量时,当钢筋处于未腐蚀状态,阴极和阳极之间的腐蚀电位差数值小于1mV。混凝土处于干燥状态时,相邻两个阳极棒之间的交流电阻数值大于100kΩ,通过外加电路检测,此时回路中的输入电流太小,很难准确获得所需要的腐蚀影响因素参数[8]。
传感器在检测过程中,当电压值小于1mV、电流处于微安级别,电阻值大于100kΩ时,系统噪声和测量噪声带来的干扰误差较大,从而影响钢筋混凝土腐蚀检测的精度。本文采用改进的自适应卡尔曼滤波算法处理未知噪声提高微弱信号的信噪比,使用新息现对估计模型的动态调整,从而提高多传感器综合检测系统的腐蚀检测精度。
3 自适应卡尔曼滤波算法研究
卡尔曼滤波算法是一种利用线性系统状态方程,对含有不确定因素的动态系统使用来提高系统预估精准度的算法[9],最优估计过程也可看作滤波过程。在多传感器测量系统,由于测量值与估计值具有几乎完全相同的概率条件,为了更好的降低误差,在假定被测系统变量变化不显著的情况下,将之前时刻的测量值随机作为当前时刻的测量值,以达到更好的降噪效果。自适应卡尔曼滤波是通过对系统噪声和测量噪声的在线估计和调整,来改进滤波设计、减小滤波的实际误差[10-11]。
3.1 自适应卡尔曼滤波最大概似方程的建立
对于多传感器检测系统模型,其状态方程和量测方程为:
Xk=Fk,k-1Xk-1+Wk
(1)
Zk=HkXk+Vk
(2)
式中:Xk为k时刻系统状态量;Fk,k-1为系统状态转移矩阵;Wk为系统噪声,其协方差矩阵为Qk;Zk为k时刻系统测量值,Hk为系统测量矩阵;Vk为测量噪声,其协方差矩阵为Rk。
由标准卡尔曼滤波方程可以得到系统滤波器的新息ek:
ek=Zk-Hkk/k-1
(3)
式中:ek是滤波器的量测残差,为了降低系统异常测量值对滤波的影响,滤波器的发散情况通过协方差与平方和计算得来,由于新息方差{ek}为高斯白噪声序列,理论协方差为
(4)
式中:Pk/k-1是预测状态的误差协方差矩阵,根据区间长度为N的新息序列{ek},可得Czk的估计值
(5)
(6)
式中:K(k)为自适应卡尔曼滤波增益,最大概似估计是要求所选样本在被选总体中出现的可能性为最大,它同时考虑新息和新息协方差的变化。不同于普通卡尔曼滤波算法,自适应卡尔曼滤波算法的核心思想是检测系统能够对测量噪声和系统噪声进行实时的估计和调整[12]。因此,利用最大概似估计准则为建立测量噪声方差阵和系统噪声方差阵的估计表达式提供了依据,极大提高了滤波精度[13-15]。
记自适应调整参数α={α11,α22,…,αnn},αii为R矩阵的噪声方差系数,采用高斯概率密度函数表示在α条件上Z的条件概率密度函数
(7)
式中:m为系统观测量数目;Czk为k时刻新息方差。对式(7)两边同时取对数得
(8)
式(8)取得最大值时需满足
(9)
根据最大概似估计准则,即满足:∂P/∂α=0,对式(9)求α的偏导,根据式(10)、(11)矩阵计算公式
(10)
(11)
整理得到
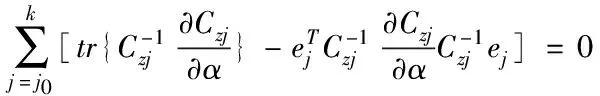
(12)
由式(4)Czk定义得Czk对α的偏导为
(13)

(14)
假设估计窗口的过程基本处于稳态,省略式(14)的第一项变为
(15)
式(15)代入式(13),Czk对α的偏导为
(16)
将式(16)代入式(12),整理得到自适应卡尔曼滤波器的最大概似方程
(17)
3.2 测量噪声协方差矩阵R的估计
本文假设系统噪声方差阵已知,与调整参数α无关,得到测量噪声方差阵,即:αi=Rii,这样式(17)变为
(18)
化简得
(19)
式(19)代入式(4)得到测量噪声协方差R的估计为
(20)
3.3 系统噪声协方差Q的估计
同样的,假设测量噪声方差阵已知,令αi=Qii,式(17)变为
(21)
(22)
式(22)代入式(21)得
(23)
因为协方差矩阵Pk/k-1为正定的,所以式(23)为
(24)
由式(24)得
(25)
根据标准卡尔曼公式Pk=Pk/k-1-KkHkPk/k-1化简得
(26)
由式(26)得系统噪声协方差的估计为
(27)
忽略状态估计方差阵的变化,系统噪声协方差Q的估计为
(28)
因此,自适应卡尔曼滤波算法计算方程为
Xk=Fk,k-1Xk+Wk-1
(29)
Pk/k-1=FPk-1/k-1FT+Qk
(30)
Kk=Pk/k-1HT(HPk/k-1HT+Rk)-1
(31)
Xk|k=Xk|k-1+Kk(Zk-HXk|k-1)
(32)
Pk|k=(1-KkH)Pk/k-1
(33)
(34)
(35)
4 仿真与结果分析
为了验证自适应卡尔曼滤波算法的效果,本文利用MATLAB进行仿真分析,与常规卡尔曼滤波算法进行了对比。输入信号含有高斯白噪声,取信噪比SNR为5dB时进行以下仿真。分别对电压、电流、电阻进行滤波对比处理,检测三种腐蚀影响因素参数在不同滤波算法下的数值变化情况。混凝土温度22℃,湿度90%,钢筋应力1670Mpa,分别用两种滤波算法进行350次仿真。仿真中对式(1)、(2)中的变量初始化如下
(36)
分别用常规卡尔曼滤波算法和自适应卡尔曼滤波算法进行仿真,结果如图2所示。
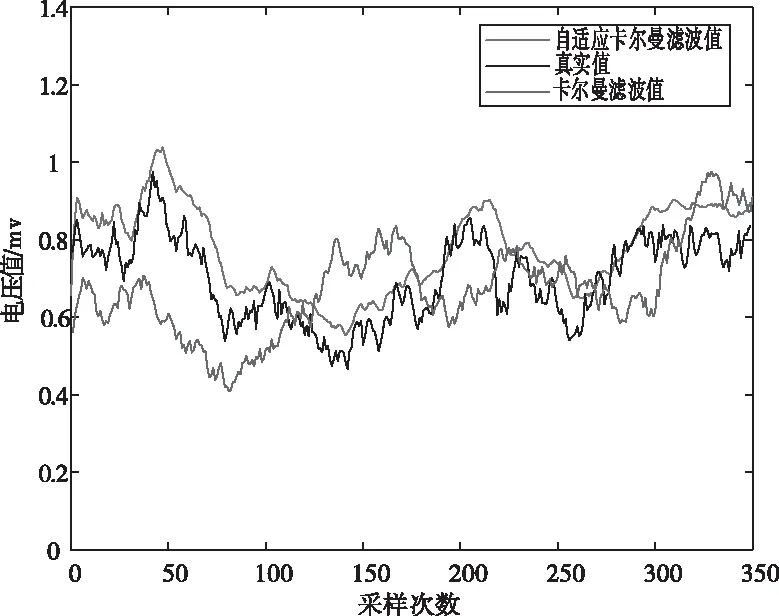
图2 电压值滤波对比
图2、图3和图4分别为电压值、电流值和电阻值进行两种滤波算法后与真实值的对比。红色线为自适应卡尔曼滤波值,蓝色线为常规卡尔曼滤波值。由上述仿真图可知,自适应卡尔曼滤波值对真实值的拟合度高于常规卡尔曼滤波算法,传感器检测数据精度得到提高。
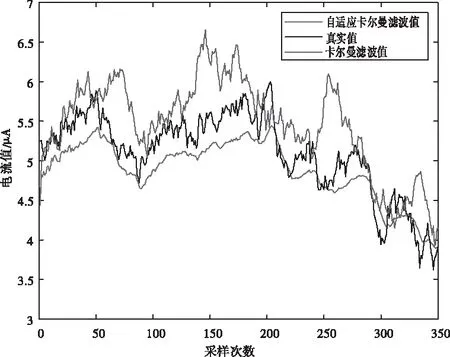
图3 电流值滤波对比
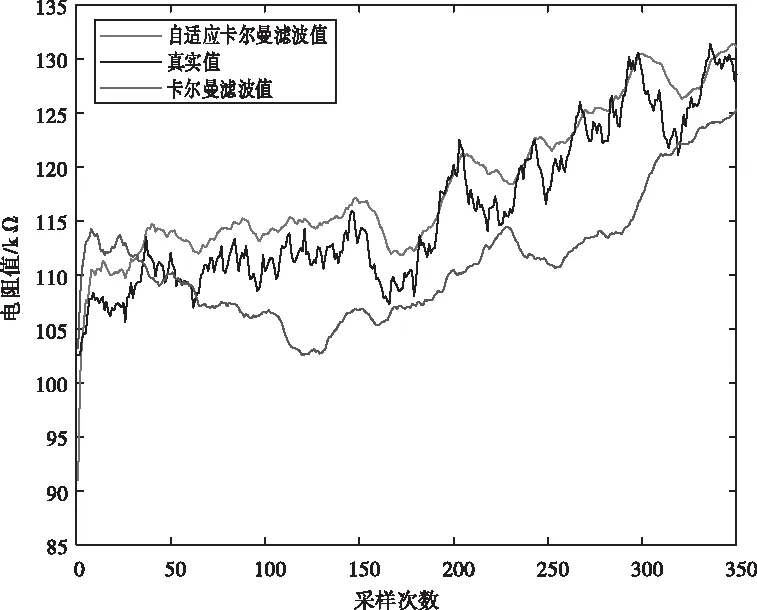
图4 电阻值滤波对比
自适应卡尔曼滤波值和常规卡尔曼滤波值与真实值之间的误差如上面的图5到图7所示。在误差仿真结果图中,红色线代表常规卡尔曼滤波值与真实值的误差大小,蓝色线代表自适应卡尔曼滤波值与真实值的误差大小。从图中可以看出,常规卡尔曼滤波误差较大且不稳定,电压峰值误差达到0.3mV,电流峰值误差达到1μA,电阻峰值误差达到9kΩ。而自适应卡尔曼滤波算法由于在滤波的同时,能够不断在线估计和修正噪声统计特性,所以其滤波误差较小且基本保持稳定。

图5 电压误差
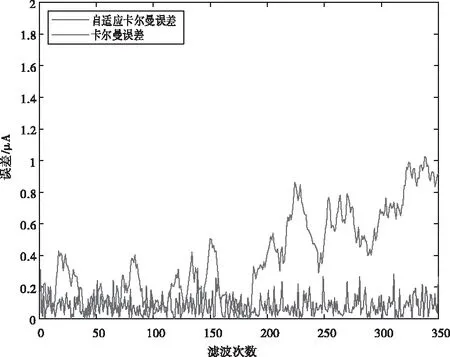
图6 电流误差
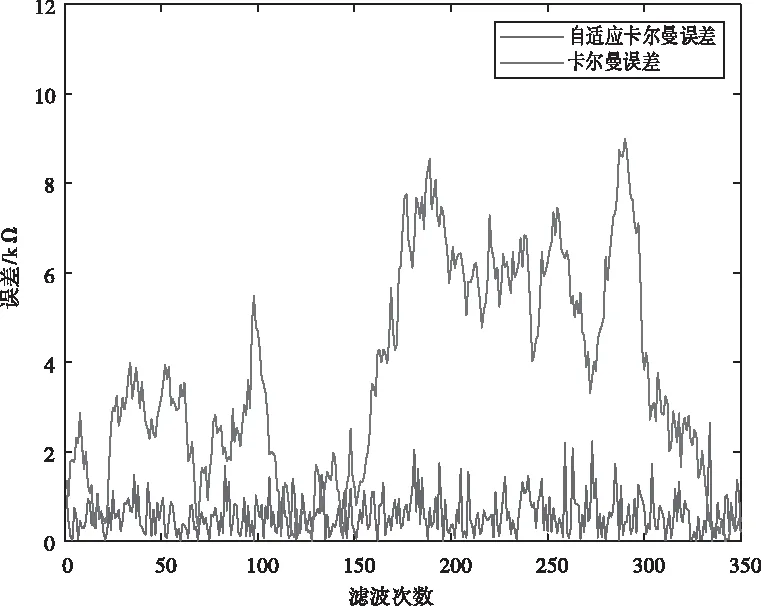
图7 电阻误差
5 结论
本文重点研究了建筑物混凝土腐蚀检测中的传感器数据滤波问题,提出了改进的自适应卡尔曼滤波算法。通过对系统噪声协方差和测量噪声协方差的动态估计,实现了多传感器检测数据的实时修正。仿真结果表明:改进的自适应卡尔曼滤波算法相比常规卡尔曼滤波算法性能得到明显提升,有效降低了多传感器系统数据测量误差,为建筑物混凝土的耐久性研究提供了基础。
