基于门槛值法的空间形态地域特征识别

陈宁静，翟玉庆

(东南大学成贤学院，江苏 南京 210032)

1 引言

空间形态地域特征是指在城乡规划过程中，由多层次的集镇、村庄及其管辖范围内分布的多种功能特征构成的空间体系。城乡相互依存，互为补充，共同构建起城乡互动的完整体系。相对于城市而言，乡村通常处于从属地位，但乡村也同样具有自己独特的内涵，是一个具有生产、生活和生态等多种功能的地域空间类别[1]。我国经济持续发展，城市经济不断向乡村渗透，乡村地域也处于转型发展与改造的过程中。

江苏地处长江经济带，是我国发展水平最高的省份之一。近年来，乡村格局的优化调控成为现阶段建设社会主义新农村的重要目标。江苏省自然环境的过渡性和区域经济文化具有较大差异，构成了多样化的乡村空间格局，也加速了乡村空间形态地域的变化程度[2]。因此，获取乡村空间形态地域特征识别信息，从而了解乡村目前发展状态，是目前学者亟需研究的重要目标。

文献[3]提出一种适用于形状固定空间网络结构的特征识别方法，选择一个典型的球面测地线网络作为初始状态，其杆长在一个极限信号内。然后，根据变换引起的杆长变化，对杆施加压缩，将该网络变换成所需的椭球形状。采用动态松弛法，通过施加残余力，对节点位置进行显式积分。在特征识别过程中，创新性地将椭球面上约束节点的边界条件视为节点位置处曲面法向上的反作用力，该反作用力与杆件上的压应力反向分量相平衡。在每个显式迭代步骤中，节点位置也根据固定的形式条件进行修正。在时间历程的序列结果中，通过适当选择收敛准则，从状态的时间历程中找到最优解。文献[4]以萝卜寨为例，提出羌族传统村落空间形态特征识别，首先分析羌族传统村落的自然形成环境，然后提出羌族村落的空间形态特征、最后分析建筑布局特色，从这三个方面分析构建传统村落的空间形态特征识别方法。

本文提出一种基于门槛值法的空间形态地域特征识别方法，实现乡村空间形态地域的结构规模和形态差异分布的格局特征，为江苏省新农村规划建设提供划分指导的研究支撑和优化调控的科学依据。

2 空间形态地域特征图像数据采集及处理

空间形态地域特征红外遥感图像数据采集系统内包含SRAM、CCD线阵相机、FPGA芯片、UART调试总线、下位机、VGA显示板块，具体系统架构如图1所示。

图1 图像采集系统架构图

由图1可知，SRAM作用于实时缓存采集的目标数据，CCD线阵相机作用于实时拍摄数据目标，UART为一种串行数据总线，和计算机进行连接，从而调试系统；下位机作用于接收FPGA处理结果的控制信号；VGA可以显现出空间形态地域特征图像处理结果。FPGA控制板块是空间形态地域特征图像采集系统的全局关键控制区域，兼顾图像的采集与处理，包括采集板块和处理板块。图像采集板块关键任务是及时保存相机拍摄的图像信息，数据处理板块主要是去除图像内的冗余信息，修复可用的真实数据，极大程度简化了数据的操作流程。

为了增强遥感空间图像成像质量，抑制图像噪声，以便对后续地域特征识别提供有效帮助，下面是对红外遥感图像进行预处理。将红外焦平面阵列各个阵元的响应率描述为

R(i，j)=Vs(i，j)/H(i，j)

(1)

式中，R(i，j)是第i行、j列阵元的响应率，Vs(i，j)是此阵元的参照辐射源反应电压，H(i，j)是阵元收到的辐射能。通过式(1)可知，针对一个匀称黑体辐射源，因为焦平面各个阵元的响应率均不相同，会致使各个阵元输出的响应也不相等，继而形成输出图像灰度分布不均特征[5]。常用的非均匀特征包含三种定义，将本文方法采用的图像非均匀特征记作

(2)

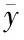
在现阶段的非均匀校准方法中，时域高通滤波算法计算简便，使用此方法可同时实现增强目标的目的。

在算法运算过程中，背景图像估算是一个重要步骤，由于图像的不均匀特性很难利用数学模型进行表达，因此在实际操作中，选择大尺度高斯滤波进行背景估算，也能得到较好的估算结果[6]。

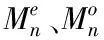
(3)

式中，en(x)、on(x)分别表示复小波转换的实部与虚部，其幅值及相位信息依次记作

(4)

Φn(x)=atan 2(on(x)，en(x))

(5)

去噪过程就是将各个尺度设定一个门限值，经过去除噪声分量来有效降低滤波器响应矢量的幅值，同时维持相位不变。相位保持方法可直接运用在加性高斯噪声过滤，拥有很好的应用空间。

基于高通滤波方法与基于相位保持的滤波方法，分别对图像灰度分布的非均匀性及噪声的控制具备一定的成效，但在多数状态下，非均匀性与噪声是同时存在的，所以要将其进行统一，确保防止出现非均匀现象的同时，实现减少噪声的目标[7]。

一般情况下，对于一幅包含噪声的红外遥感图像I(x，y)而言，将其定义为

I(x，y)=S(x，y)+η(x，y)

(6)

式中，S(x，y)是待评估的真实图像，η(x，y)表示噪声分量。灰度分布非均匀特征会致使图像信噪比大幅降低，非均匀特征也是一种空间噪声，所以，把噪声分量η(x，y)描述为

η(x，y)=ηr(x，y)+ηs(x，y)

(7)

式中，ηr(x，y)是随机噪声，ηs(x，y)代表空间非均匀特征噪声。

利用以上建立的红外遥感图像噪声模型，融合高通滤波的非均匀校准定理保持滤波方法，设计一种改进的滤波算法[8]，把非均匀性校准加入相位保持方法内，具体计算过程如下：

3 基于门槛值法的空间形态地域特征划分模型

门槛值回归模型的基础模式为：

yit=μ+Xit(qit<γ)β1+Xit(qit>γ)β2+ui+eit

(8)

式中，qit是门槛变量，γ是对应的门槛值，其系数依次是β1、β2，参数ui表示个体反应，eit为随机干扰项。也可将该模型变换成

yit=μ+Xit(qit，γ)β+ui+eit

(9)

(10)

如果γ的值是已知量，利用最小二乘估计获得β的估算值为

(11)

式中，y*与X*表示组内误差。若要明确γ值就必须要搜寻门槛变量集合qit，无需搜寻全部样本[9]。γ的估算值为残差平方和的最低值，具体公式为

(12)

4 基于改进型PCNN赋时矩阵的地域特征识别方法

传统PCNN模型公式为：

Fij[n]=exp(-αF)Fij[n-1]+VF+Iij

(13)

Lij[n]=exp(-αL)Lij[n-1]+VL

(14)

Uij[n]=Fij[n](1+βLij[n])

(15)

(16)

θij[n]=exp(-αθ)θij[n-1]+VθYij[n]

(17)

式中，下标ij表示神经元标号；n是迭代次数；Iij、Fij[n]、Lij[n]、Uij[n]、θij[n]依次为神经元的外部作用、第ij个神经元第n次回归输入、相连输入、内部运动值及临界值；M、N是链接权值矩阵；VF、VL、Vθ分别表示Fij[n]、Lij[n]、与θij[n]的幅度常数，αF、αL、αθ是对应的衰退指数，β是链接指数。

图像处理的过程中，把二维网络M×N神经元依次和输入图像M×N像素相对照，生成输出序列Y[n]。Y[n]内拥有图像边缘位置和纹理特征数据，完成特征数据识别。

因为传统神经元L通道内信号拥有一定程度的冗杂性，它的大小和通道变量、神经元相邻区域的点火神经元个数相关，引发了神经元的冗杂性，不利于得到物理概念清楚的可靠算法。

此外，ULPCNN模型内即便临界值为指数衰降，但转换效率过高，此种临界值机制导致图像处理后，依旧存在数量众多的信息隐藏于神经元的频度内[10]，处理后的输出图像涵盖的信息完整度不高。

为了改善上述不足，本文在传统PCNN的前提下，对ULPCNN采取简化，将临界值函数进行修复改进，也就是将伴随时间反复变化的指数函数转换为伴随时间单操控下降函数，同时融合神经元之前输出的每个次脉冲信号[11-12]。在妥善思考图像处理的局部数据状态下，加入局部离散系数，继而让统计特性的链接强度βij完成自适应，将此过程用离散数学解析式表示为

Fij[n]=Iij

(18)

(19)

Uij[n]=Fij[n](1+βij[n]Lij[n])

(20)

(21)

式中，βij可通过图像处理的局部数据采取自动调节，θθ实现自动调节时，应当择取空间形态地域特征图像整体像素最大灰度数值Imax，也就是θθ=Imax，以此AUPCNN模型内能够设定的参变量就仅有αθ，大幅提升了模型自适应稳定性。在βij≠0的情况下，神经网络的处理效率不仅能获得像素对照神经元数据，还可得到相邻位置的有关数据。

在图像迭代处理过程中，设定一个赋时矩阵T，在T内保存和各个神经元点火时段相关的时间数据，将其描述为

(22)

赋时矩阵呈现出图像空间内的时间数据，迭代过程一直持续至全部神经元后，T内因子值都不是0为止，最终构成PCNN赋时矩阵T。

在物理学中，将一个平面离散质点系的质心描述成

xc=∑xrmr/∑mr，yc=∑yrmr/∑mr

(23)

式中，mr是坐标(xr，mr)位置质心质量，∑mr是质点系质量，(xc，yc)是指点系的重心，映射出质点系形态、体积和紧密系数等固有特征。本文把这个理论加入到图像特征识别中，采用PCNN处理之后，将其引入图像像素部分相邻时间数据赋时矩阵内

为了对不同内容和大小的图像进行赋时矩阵中心特征识别，将其采取归一化处理，表示为

ic0=ic/M，jc0=jc/N

(24)

PCNN赋时矩阵中心特征可以维持图像良好的不变性，保证不同图像具备不同的赋时矩阵重心特征，实现精准的空间形态地域特征识别。

5 仿真研究

为了验证本文方法的实用性，将地形图当作乡村的区域位置，每个图斑都是一个待识别目标，用等距离的空间最小可识别目标序列当作尺子，运用不同的尺子对待识别目标实施测量。

图2、图3是本文方法的特征识别性能仿真结果，从图中可知，在空间最小可识别单元的对数值高于11.64时，双对数曲线虽然没有过多的线性改变，但近似和线性拟合曲线重叠，其浮动在有限范围内的幅度较小，可将其浮动当做线性变化；对数值低于11.64时，双对数曲线远离线性拟合曲线，倾斜率变化比较明显，呈现出非线性关联趋势。虽然二者存在不一致区域，但线性区域基本能够重叠，可将其当作线性区域的可靠认证，继而明确了特征分布的存在区域范围，实现了特征区域的准确划分。

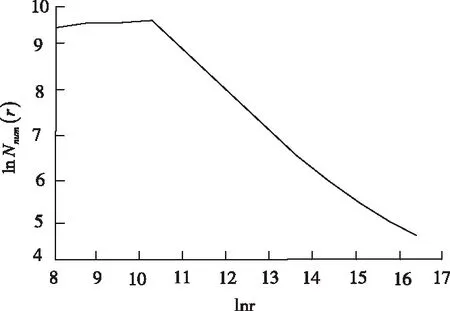
图2 空间最小可识别目标和双对数乡村数量曲线

图3 空间最小可识别单元与双对数乡村面积曲线

为了进一步验证本文基于门槛值法的空间形态地域特征识别方法的有效性，利用文献[3]方法和文献[4]方法对比分析空间形态地域特征耗时情况。表1是三种方法空间形态地域特征识别耗时对比结果。

表1 不同方法空间形态地域特征识别耗时/s

从表1可以看出，对比文献[3]方法和文献[4]方法，本文方法识别耗时较短，具备较高的识别效率，能够完成空间形态地域的高效率识别，保证乡村规划过程的可靠性与高效性。

6 结论

为了进一步提高乡村空间形态地域分布特征识别精度，提出一种基于门槛值法的空间形态地域特征识别方法。搭建红外遥感图像数据采集系统，通过融合高通滤波的非均匀性校准和相位保持的去噪方法，抑制红外图像灰度分布不均现象，剔除噪声影响，完成图像数据采集和处理；利用基于门槛法的空间形态地域特征划分模型，区分不同空间形态地域的基础特征，对ULPCNN阈值函数及链接强度进行修正改进，得到一个从空间图像信息到时间信息的赋时矩阵映射图，采用物理学相关概念定义赋时矩阵重心不变特性，实现高效率空间形态地域特征识别，为江苏省乡村规划建设提供有效帮助。