面向高维大数据的局部离群点并行检测算法

2022-03-15何美玲李佩雅

计算机仿真 2022年2期

何美玲，李佩雅

(1.浙江中医药大学信息技术中心，浙江杭州 310000；2.暨南大学网络空间安全学院，广东广州 510632)

1 引言

在数据挖掘研究领域中局部离群点检测算法可以发现高维大数据集中存在的异常数据，是重要的研究方法之一[1]。目前的检测算法面向高维大数据时，无法准确获取局部离群点的属性，花费大量的时间也无法有效的检测到局部离群点，对数据采集和应用产生严重的影响[2]。因此，需要在高维大数据环境下研究局部离群点检测算法。丁天一[3]等人提出基于相似度剪枝的离群点检测算法，该算法对数据点之间的相似度进行计算，并利用数据点对应的相似度组成相似度矩阵，构建离群点候选集，对非离群点在检测之前做剪枝操作，通过LOF算法在离群点候选集中计算数据点的局部离群因子，根据计算结果实现局部离群点的检测。但该算法没有对高维大数据进行降维处理，容易受到“维度灾难”的影响，导致检测精度较低。刘芳[4]等人提出基于密度的局部离群点检测算法，对LOF和融合索引结构进行分析，根据分析结构制定剪枝方案，在数据稀疏区域中根据剪枝方案获取初始局部离群点，并对剪枝临界值进行设定，实现局部离群点的检测，该方法未对高维大数据进行降维，剔除数据中的无用特征，导致整体检测率较低。毛亚琼[5]等人提出一种引入局部向量点积密度的高维数据离群点快速检测算法，首先以保存少量中间结果的方式只对窗口内受影响的数据点进行增量计算，同时设计2种优化策略和1条剪枝规则，减少检测过程中各点之间距离的计算次数，降低算法的时空开销，但该方法未对高维大数据进行降维处理，消除无用的数据对象、缩小数据集的容量，导致检测效率过低，不能被广泛使用。为解决上述问题，提出面向高维大数据的局部离群点并行检测算法，首先基于E-PCA算法对高维大数据进行降维处理，然后面向高维大数据从离散点集合和离群点检测算法并行化两方面实现局部离群点并行检测算法设计，最后通过仿真验证所提算法的有效性。

2 基于E-PCA算法的高维大数据降维处理

数据降维是从高维数据中检测局部离群点的必要步骤[6]。所提算法采用E-PCA算法实现高维大数据降维处理。

1)特征值与特征向量筛选

设A为对称矩阵，该矩阵可以在维度空间中描述正交分解操作，反映在不同特征向量中对称矩阵A对应的投影长度，特征值可以通过投影长度计算得到，获得特征值为K的分量在投影前对应的值，并丢弃其余分量，降低对称矩阵的维度，保留有效信息[7]。

2)信息熵

(1)

式(1)中，信号信息熵的单位为bit。设信息熵阈值为δ，通过设定的阈值判断保留或剔除特征，δ通常情况下可通过以下方法计算得到：

①根据应用分析中特征对应的重要性进行判断，无用特征信息对应的熵值和有用特征对应的熵值之间的差异较大；

②通过下述公式对原始数据中特征对应的比重进行计算

(2)

根据上述信息熵阈值判断方法，得到如图1所示的Arcene数据集中数据点对应的信息熵值构成的曲线图。

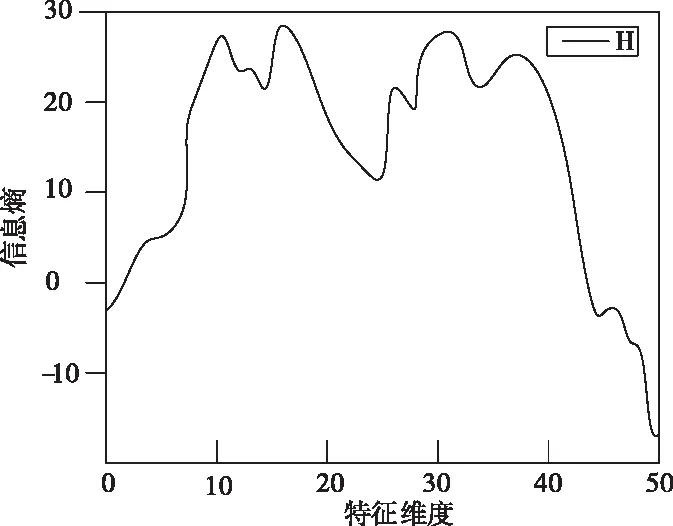
图1 数据集前50个属性的信息熵值

3)E-PCA降维算法

面向高维大数据的局部离群点并行检测算法采用E-PAC算法消除高维大数据中存在的冗余数据，基于信息熵的高维数据降维处理具体流程如图2所示[8]。

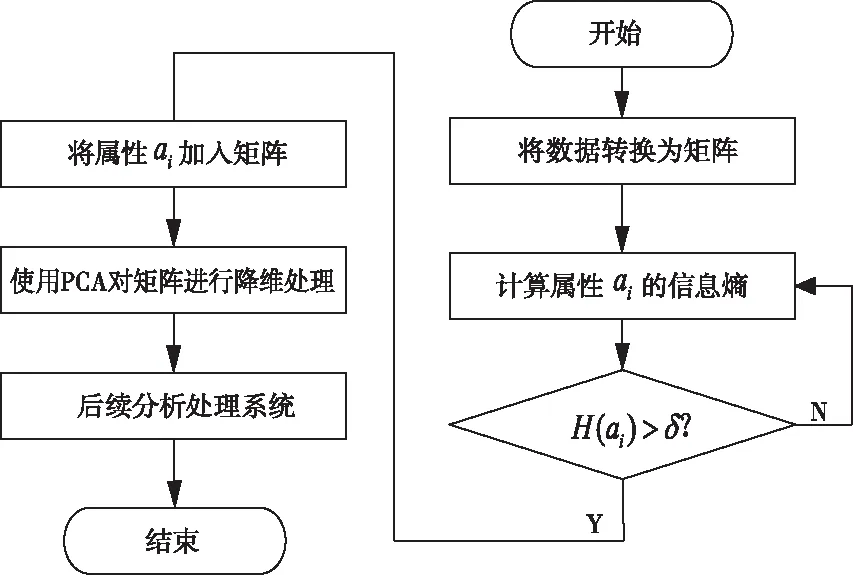
图2 基于信息熵的高维数据降维处理流程

根据图2所示的基于信息熵的高维数据降维处理流程，首先用描述数据矩阵，其中，m代表的是样本数量；n代表的是特征数量；f代表的是贡献率；Yk*m代表的是降维后的数据，则得到E-PCA算法的具体步骤如下所示：

步骤一：计算每个属性对应的信息熵值，并将计算结果与设定的阈值δ进行对比，消除冗余特征，对U进行以下计算：为了使i=1，计算属性ai对应的信息熵H(ai)，如果H(ai)>δ，在集合A中存储属性ai；

步骤二：样本矩阵中心化，得到矩阵Xn*m，其中，X的关系表达式如式(3)所示

X=A-repmat[mean(A，2)，1，m]

(3)

步骤三：对属性不同维度之间存在的协方差进行计算，根据计算结果组成协方差矩阵cov，其关系表达式如式(4)所示

cov=XXT/[size(x，2)-1]

(4)

步骤四：计算cov 的特征值与特征向量；

步骤五：通过上述过程计算得到的特征值和特征向量构建特征向量矩阵Vn*k；

步骤六：通过下述式(5)实现降维

Y=VTX

(5)

步骤七：算法结束，在特征值贡献率f的基础上确定参数k

(6)

3 面向高维大数据的局部离群点并行检测算法

3.1 离群点集合

当高维数据进行降维处理后，消除了高维数据中存在的无用数据，并减少了高维数据集的容量，为了提高局部离群点的并行检测效率，在计算可达距离时，需要改进传统的LOF算法，具体过程如下：设D′代表的是高维数据集；E代表的是离群点构成的集合；ξ代表的是离群因子对应的阈值。

步骤一：对任意对象y(y∈D′)的k-y距离k(y)进行计算，根据计算结果获取y的距离邻域Nk(y)；

步骤二：计算y与s(s∈D且s≠y)之间存在的可达距离；

步骤三：当对象s和对象y都不属于中心点时，利用式(7)对可达距离reachdist(s，y)进行计算：

reachdist(s，y)=max{k(y)，dist(s，y)}

(7)

步骤四：如果对象s、y都是簇Cl和Cm的中心点，此时可达距离如式(8)所示

(8)

步骤五：如果对象s、y只有一个是簇Cl的中心点，可达距离的计算如式(9)所示

(9)

此时y的局部可达密度如式(10)所示

(10)

步骤六：根据步骤二～步骤五利用对应的公式对不同对象对应的局部可达密度进行计算；

步骤七：通过式(1)获得对象对应的局部离群因子

(11)

步骤八：当ξ

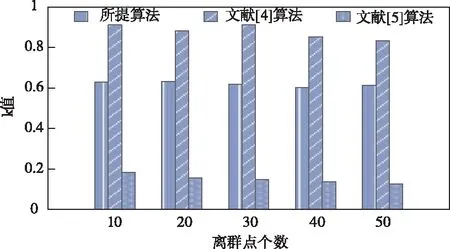
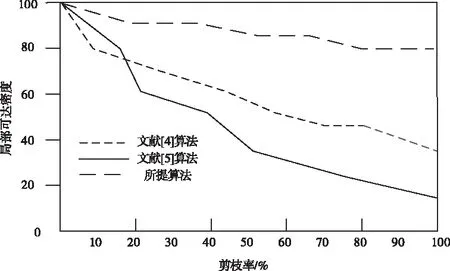
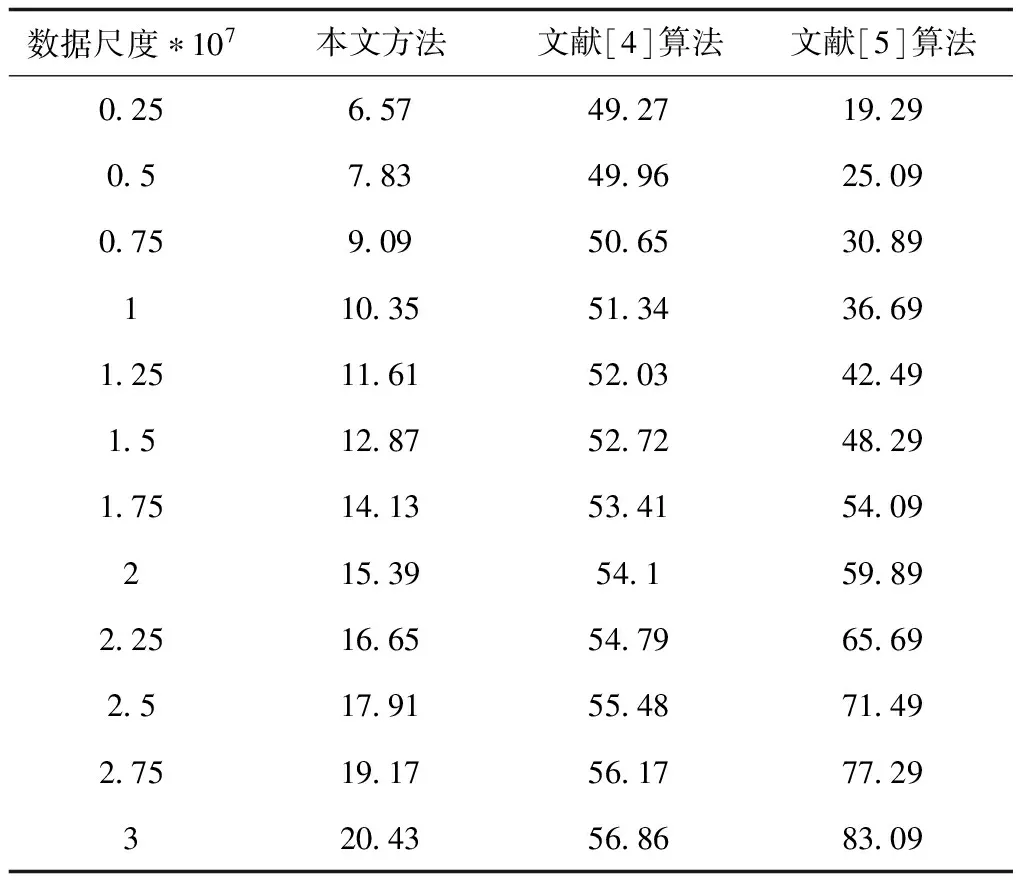
3.2 离群点检测算法并行化

面向高维大数据的局部离群点并行检测算法将Hbase作为数据源，在Hadoop平台中完成局部离群点的并行检测，具体过程如下：

步骤一：采用DSP算法均匀划分输入的原始数据集D，获得若干个数据块，在DataNobe节点中存入获取的数据块[10]；

步骤二：利用获取的数据块建立键值对〈K，V〉，其中K代表的是行号，V代表的是字符串中存在的内容。在Reduce阶段中对数据进行过滤处理，获得属性值，输出〈id，property〉，其中，id值代表的是能够反映数据对象xi的一种标识，property描述的是xi对应的属性值，表达式如式(12)所示

{xi1，xi2，…，xin}

(12)

步骤三：输入〈id，property〉，在Map阶段不做处理，在Reduce阶段根据式(13)计算所有对象xi与其它对象的距离dist(xi，xj)，输出键值对〈id，dist〉，dist中表示xi的与其它对象的距离dist(xi，xj)值，并存入输出文件中

(13)

步骤四：输入步骤三产生的键值对〈id，dist〉，在Map阶段不做处理，在Reduce阶段计算出xi的距离领域，输出键值为〈id，neighbor〉，其中neighbor表示每个数据对象xi的距离邻域N∈(xi)；

步骤五：输入步骤四产生〈id，neighbor〉，Map阶段根据式(14)确定核心对象集O，在Reduce阶段确定簇划分C={C1，C2，…，CK}，输出〈c，object〉，其中，c代表的是簇类号；簇中对象为object，得到核心对象集O如式(14)所示

O=O∪{xj}

(14)

步骤六：输入步骤五产生的键值对〈c，object〉，Map阶段融合步骤二产生的键值对，并根据式(15)分别计算各簇Cl的平均距离avg(Cl)、最大距离diam(Cl)

(15)

在Reduce阶段根据式(16)找出各簇的中心点μ={μ1，μ2，…，μk}

(16)

初步确定离群数据集D′=D/C∪μ，输出〈D′id，Ccore〉。其中，Ccore代表的是集群点最大距离；D′id代表的是数据对象；

步骤七：输入上述过程计算得到的键值对〈D′id，Ccore〉，并在Map阶段中对〈id，dist〉进行融合处理，根据3.1节的步骤一获取的各对象对应的距离邻域，在Reduce阶段根据3.1节的步骤二～步骤五计算其对应的可达距离，输出〈D′id，reach〉；

步骤八：输入步骤七产生的键值对〈D′id，reach〉，在Map阶段根据3.1节的步骤六计算离群对象的局部可达密度，在Reduce阶段根据3.1节的步骤七计算各个对象的局部离群因子，输出键值对〈D′id，lof〉，其中，lof代表的是数据对象的局部离群因子；

步骤九：输入步骤八产生的键值对〈D′id，lof〉，在Map阶段不做处理，再在Reduce阶段根据3.1节步骤八找出离群对象，输出键值对〈Outlierid，Outlierlof〉，其中，Outlierid代表的是离群对象的id；Outlierlof代表的是离群对象的离群因子。

综上所述可知，当前的局部离群点检测算法受到“维度灾难”的影响，在处理大规模数据上存在很多不足，因此，所提方法首先对高维数据进行降维处理，然后将传统的离群点检测算法(LOF)和Hadoop分布式平台下的Mapreduce分布式框架结合，得到初始离群数据集，再对传统的LOF算法进行相应的改进，计算局部离群因子，找出高维数据中的离群点集合并判断其准确位置，实现局部离群点并行化检测。

4 实验分析

为了验证面向高维大数据的局部离群点并行检测算法的整体有效性，需要对面向高维大数据的局部离群点并行检测算法进行仿真测试。分别采用所提算法、文献[4]基于密度的Top-n局部异常点快速检测算法和文献[5]引入局部向量点积密度的数据流离群点快速检测算法进行检测k值、局部可达密度和检测时长对比测试。

4.1 k值测试结果

k值的选择会引起局部离群因子LOFk(y)值的波动，k值太小虽能减少计算量，但会降低检测准确率，k值太大，计算开销会急剧增大，因此将k值作为测试指标对所提算法、文献[4]算法和文献[5]算法进行测试，结果如图3所示。

图3 不同算法的k值对比结果

由图3不同算法的k值对比结果可知，文献[4]算法的k值在0.8以上，相对较高，计算开销急剧增大；文献[5]算法的k值低于0.2，相对较低，计算开销较小；所提算法的k值稳定在0.6附近，表明该算法能够有效并行检测高维大数据中的局部离群点。原因是所提算法在对局部离群点并行检测前，采用E-PCA算法对高维大数据进行了降维处理，避免受到“维度灾难”的影响，出现离群点被冗余维度属性所掩盖的现象，进而稳定了k值。

4.2 局部可达密度

将局部可达密度作为测试指标对所提算法、文献[4]算法和文献[5]算法进行测试，结果如图4所示。

图4 不同算法局部可达密度对比结果

图4中剪枝率代表的是离群点所占百分比。分析图4的不同算法局部可达密度对比结果可知，随着剪枝率的增大，局部可达密度呈下降趋势，但是所提算法的局部可达密度依旧是三种算法中最高的在80以上，因为该算法利用了对局部离群点进行检测之前，提取了高维大数据的特征，并进行了特征筛选，保留了有效特征，完成了高维数据的降维处理，降低了检测的数据量，因此，该算法的局部可达密度也明显高于其它方法。

4.3 数据尺度

取k值为0.6，特征维度为5，分别测试所提算法、文献[4]算法和文献[5]算法在不同数据尺度下的检测时长，结果如表1所示。

表1 不同算法检测时长对比结果(ms)

由表1不同算法检测时长对比结果可知，随着数据尺度的增加，局部离群点检测时长增长。对表2的数据分析可知，与文献[4]算法和文献[5]算法相比，所提算法的检测时长最快，最短为6.57ms。因为该算法在实现局部离群点并行检测之前，结合了E-PCA算法对高维大数据进行了降维处理，剔除了无用的数据对象，缩小了数据集的容量，降低了数据尺度对检测时间的影响。