一种互联系统的分布式结构控制器设计方法
2022-03-15杜俊鹏关燕鹏
杜俊鹏,关燕鹏
(山西大学自动化系,山西 太原 030006)
1 引言
现实生活中存在着一种系统,如电力系统、通信系统、石化系统等,它们都具有结构复杂、关联性强、功能全面、影响因素多的特点。称之为互联的大系统[1-5]。特别是随着互联网的兴起和发展,这一跨地区甚至跨国家的大规模互联系统承担着科研、教育、商务等重要任务,发展迅速,为社会经济发展创造了巨大效益。
对于每一个大型互联系统,如何建立子系统以及如何规划子系统之间的连接和协调是核心问题。通常需要部署一系列的控制器,以便对每个子系统进行有效和高效的监视和控制。传统上,这种设计过程是以分散的方式实现的,即每个控制器只能从自己的子系统感知测量信息,然后实现对自己子系统的控制输入。这种去中心化的配置结构具有计算量小、设计复杂程度低等优点,但同时也不可避免地导致了系统性能的恶化和网络环境中应用范围的限制。事实上,随着通信技术和互联网技术的发展,控制器可以在地理上分布,也可以远程调度。每个本地控制器的信息可以通过一个共享的通信网络在它的邻居之间进行交换。这样,每个控制器可以使用更多的反馈信息,这就意味着整个互联系统的控制性能有望得到改善。
基于以上讨论,本文考虑了网络系统中各子系统控制站之间通信拓扑的设计问题。首先,如果在每个子系统中都设置一个控制器,并在每个子系统与其它子系统之间建立一个通信通道,显然对管理者最有利,并且能够以最好的效果管理整个控制系统。然而,这种方法在实践中往往是行不通的。一方面,一般不需要在每个子系统之间建立通信通道,这样会产生大量的冗余;另一方面,建设成本也是一个考验。因此,如何利用较少的通信信道来达到预期的控制效果是讨论的核心问题。那么应该在哪些控制器之间搭建通信信道呢?在现有的分布式控制结果中,分布式控制器之间的耦合关系通常用固定加权图来描述,因此是预先确定的。换句话说,空间分布式控制器的通信拓扑结构是预先给定的,在整个设计和实现过程中保持不变。但是,从工程的角度来看,确定一个控制器是否应该从另一个控制器获取信息可能并不容易,因为必须在安装成本和系统性能的变化之间进行权衡,而这是事先不确定的。因此,在充分考虑系统性能要求的前提下,对网络化互联系统控制器之间的连接进行调度是十分必要的。
本文假设满足实际系统的通信信道的数目是一个固定值,以此平衡通信成本和控制性能,即将此问题转化为一个稀疏优化问题来处理。稀疏优化是相关领域的一个研究热点[6-10]。在文献[6]中,设计了一种交替方向乘子法的稀疏约束方法,经验证可以用一个设定值控制矩阵的稀疏水平;文献[7]研究了一类约束条件下的最优控制问题,它可以在不增加有限维的情况下求解稀疏最优控制问题;文献[8]中,将一种稀疏正则化原理,应用于对模糊图像的盲复原上,对目标图像进行稀疏正则化约束,得到了稀疏性正则化约束目标图像复原模型。
然后,把稀疏优化问题转化为一种势约束问题,由于势约束问题的复杂性,它通常是一种非线性的难解的问题[11],通常能在投资学、金融学、运筹学等涉及优化博弈的领域见到这种问题。在本文中,采用一种混合整数放松法来解决这种问题。
2 问题描述
2.1 系统框架
如图1所示,考虑一个由以下形式的p个子系统组成的互联系统
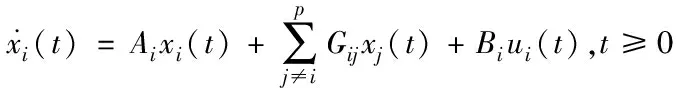
(1)
其中:i,j∈{1,2,…,p},xi(t)∈Rni为系统状态向量,ui(t)∈Rmi为系统控制输入向量,Ai,Bi和Gij表示具有合适维度的常数矩阵,子系统i和子系统j通过Gij或Gji物理连接,如果子系统j和i之间没有互相影响,那么耦合矩阵Gij=0。假设系统没有丢包现象,所有状态都可以测量,分布式网络化控制系统结构图如图1所示。

图1 互联系统的分布式控制框架
2.2 问题提出
分布式控制系统分为p个子系统,具有分布范围广、传感器数量多、对网络传输能力要求高的特点。控制器设计形如(2)式所示
(2)
其中,Ki是控制器增益矩阵,Fij是需要去确定的具有适当维数的耦合矩阵。从式中可以看出,非零Fij意味着控制器i可以利用xj(t)的信息,而Fij=0意味着i不能利用xj(t)的信息。也就是说,一个非零Fij意味着控制器i和j之间存在着一个有向通信信道。
在现有的相关文献中,一般认为控制器只能从相邻的控制器获取信息[12-14],通常控制器之间的通信关系是随机设置的,不能确定应该提前在哪些控制器之间设置通信连接。在通信时,通过设置尽可能多的通信通道来满足系统的需要。这样虽然保证了系统的稳定性,但也会在一定程度上浪费资源,建立过多的通信渠道,还容易导致网络攻击[15],系统的安全性越来越差。在本文中,对控制器之间的耦合通信通道的数量进行了约束,该约束等价于非零耦合矩阵Fij的数量。
在上述分析的基础上,给出以下关于通信信道数量限制的定义
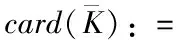
(3)
然后将为互联系统(1)中设计的分布式控制器可以表示为
(4)
其中
而0≤κ≤p(p-1),表示给系统设置的控制站之间耦合连接的最大允许数目,如果一个分布式控制器满足(4)式,就称其为具有稀疏结构的分布式控制器。
注1:从(4)中可以看出,如果整数κ=0,设计的分布式控制器将变成一个分散控制器,而在κ=p(p-1)的情况下,分布式控制器的效果将相当于集中控制器,每一个控制器可以使用所有子系统的状态信息[16,17]。
根据上述分析,得到分布式网络闭环控制系统如下
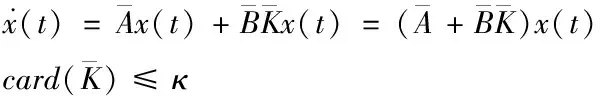
(5)
其中
x(t):=col{x1(t),x2(t),…xp(t)}
以及
(6)
3 集中式控制器设计
在本节中,将建立一个保证闭环控制系统呈指数渐近稳定的充分条件。使用李雅普诺夫方法来证明系统的稳定性。首先引入一个李雅普诺夫函数
V(t,x(t))=xT(t)Px(t)
(7)
式中P为正定矩阵。
对李雅普诺夫函数关于时间t求导可得
(8)
结合式(5),上式可表示为
(9)
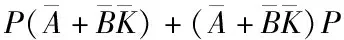
(10)
可以看出(10)中,存在非线性项,而非线性项不利于问题的解决,对式子两边同乘一个P-1,于是上式变为
(11)
然后对上式进行变量代换,令
(12)
于是(11)式变为
(13)
(13)式为一个不存在非线性项的线性式子,当该式成立时,则系统稳定。
4 结构控制器设计
基于前面稳定性分析的结果,本节将对如何设计分布式稀疏控制器进行具体介绍。受[18,19]中预先设定的势约束的重新提法的启发,得到了以下结果。
(14)
(15)
利用混合整数法,可以将势约束问题转化为一个混合整数规划的线性问题,这类线性的规划问题可以通过各类线性处理工具比较容易的解决。
然后,考虑了基于上述算法的标准放松
(16)
这里当将yl的取值变成了一个范围,这并不是很大的变化,但是它拓宽了可行域,一定程度上提高了系统的自由度,此时系统的可行域如图2所示。然后继续考虑增加系统的可行域,首先,定义函数
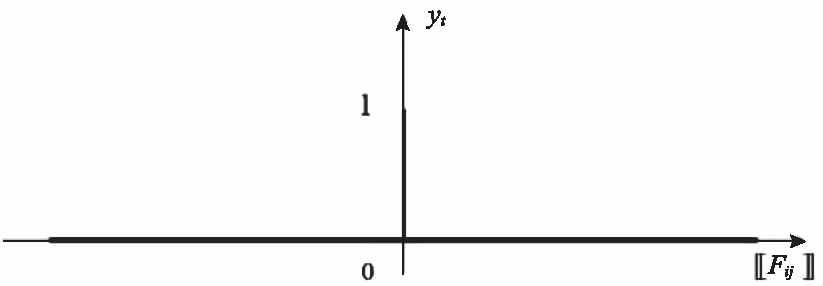
图2 放松后混合整数法的可行域
(17)
以及
(18)
当d≥0时,可以证明
(19)
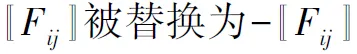
(20)
然后再次展开系统的可行域,如图3所示。
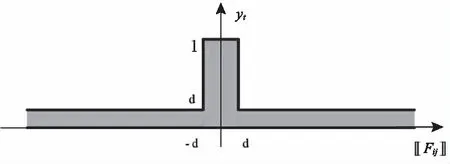
图3 再次放松的可行域
综上,带有势约束的优化问题由于其复杂性通常难以解决,通过定理1,将这种约束问题转化为一种放松方法进行求解,然后通过yalmip、cplex以及groubi等工具箱可以有效地解决该问题。
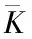
结合定理1和(13)式稳定性分析条件,即可设计出满足稀疏约束要求的分布式网络结构控制器。
5 仿真例子
在本节中,选择了一个三机电力系统模型进行仿真,以证明上述方法的有效性(对于电力系统的更多动力学和建模,可以参考文献[19,20])。它的分布式控制系统由三个子系统组成。每个子系统如下所示
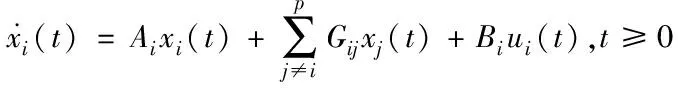
(21)
其中,xi(t)=col{θi(t)-θi0,ωi(t),Pi(t)-Pi0,Xi(t)-Xi0}表示第i个子系统的状态向量;θi(t)表示第i个机器的转子角度;ωi(t)表示第i个机器的相对速度;Pi(t)表示第i个机器的机械功率;Xi(t)表示第i个机器的蒸汽阀门开度;θi0,Pi0,Xi0是前面这些参数的标称值;参数矩阵如下所示
(22)
式中,Dci,Hi,ω0以及矩阵中的其它参数代表了电力系统中的阻尼系数、惯性常数、涡轮增益等相关参数。
矩阵Ai和Bi中的参数值如表1、2所示
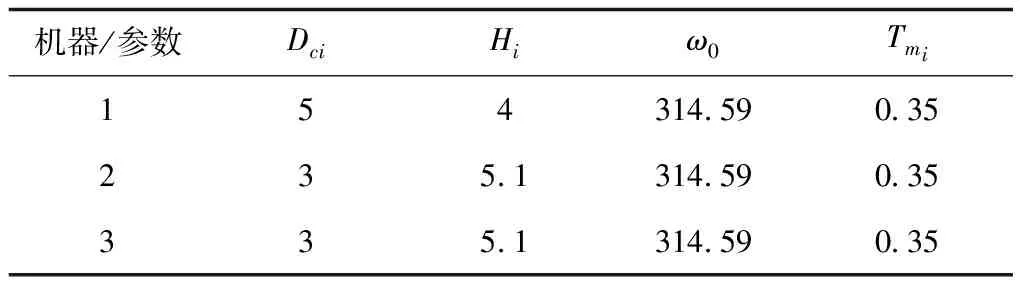
表1 矩阵Ai和Bi中的参数
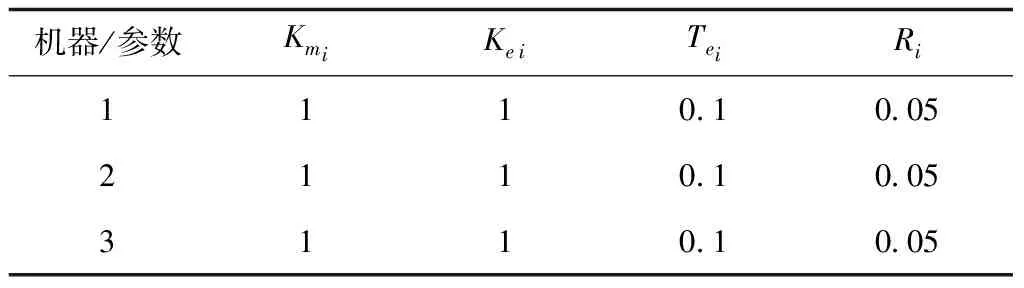
表2 矩阵Ai和Bi中的参数
矩阵Gij中的参数值如下所示
β12=β13=-27.49
β21=β23=-23.10
β31=β32=-23.10
(23)
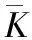
(24)
其中
(25)
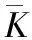
仿真时,取以下数据为初始条件
Matlab仿真得到的三个子系统的状态响应如图4、5、6所示。从图中可以看出,系统是指数稳定的,这也支持了之前的理论推导。
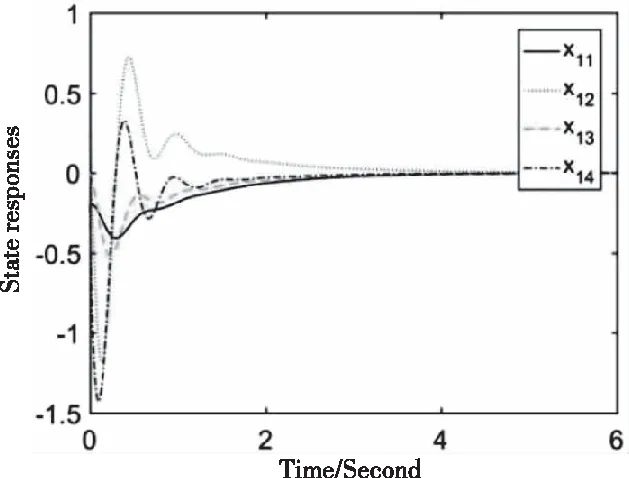
图4 电力系统子系统1的状态响应
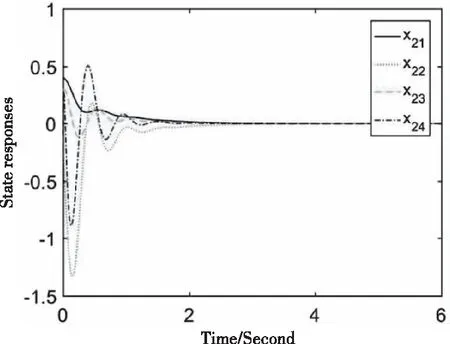
图5 电力系统子系统2的状态响应
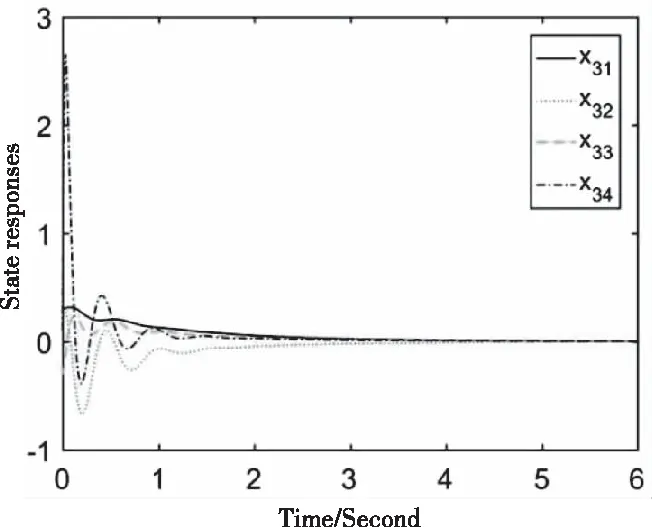
图6 电力系统子系统3的状态响应
6 结论
本文提出了一个基于混合整数放松方法的分布式网络结构控制器设计方法,分布式控制器之间的耦合连接的数量用κ来约束。该方法解决了一类势约束难题,通过扩展可行域的方法使问题变得更方便、更自由。然后用李亚普诺夫泛函分析了系统的稳定性。最后,以电力系统为例说明了该方法的有效性。
