基于特征跟踪的人机交互多点手势识别仿真

王文斌，李 琨

(1.武汉工程大学邮电与信息工程学院，湖北 武汉 430073；2.湖北大学知行学院，湖北 武汉 430011)

1 引言

目前人机交互方式不断向着人工智能化发展，如人脸识别、指纹识别、手势识别等，其中手势作为日常肢体语言的表达形式之一，其包含的信息量巨大，且具有形象和直观等优势，简单来说手势识别就是通过人类肢体动作控制设备或与设备沟通的一种方式[1-2]。利用手势识别方式可减少用户使用设备操作步骤，无需与设备发生任何物理接触。此技术被广泛应用在汽车、医疗、航天等各个领域。随着手势识别的应用面越来越广，研究手势识别的专家众多，其中以张哲等人[3]提出的多层卷积特征的手势识别方法和田元等人[4]提出的基于Kinect的实时手势识别方法使用范围最为广泛。前者利用深度学习神经网搭建识别框架，利用支持向量机算法实现手势特征识别，由于手势图像特征贡献率不同，导致浅层特征无法识别，因此识别效果不理想。后者以手势复杂背景为出发点，使用体感设备完成手势识别，由于体感设备移动性较差，因此该方法仅适用于无需设备移动场合。

针对上述情况，本文利用特征跟踪可有效获取目标静、动态特征的优势，以手势特征跟踪为出发点，对基于特征跟踪的人机交互多点手势识别展开仿真。

2 基于特征跟踪的人机交互多点手势识别

2.1 多点手势特征提取

手势特征提取时，识别信息源是关键。本文将高斯曲率应用于手势识别信息源，利用高斯曲率展示手势识别信息源的内在多点特征[5]，且不受信息外在特征影响。多点手势特征提取流程如图1所示。

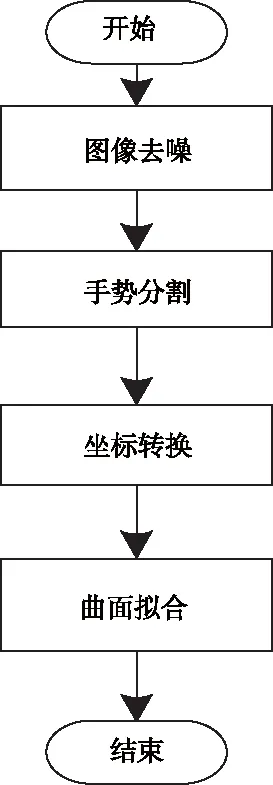
图1 手势特征提取流程

2.1.1 手势图像预处理

由于手势图像在人机交互过程中受红外光反射以及交互环境影响，存在大量噪声，因此在提取手势图像多点特征之初，需对手势图像进行噪声干扰去除[6]，本文利用滤波去除手势图像噪声，并利用归一化方法将该手势图像转换为灰度图像和距离直方图，在手势距离直方图内，手势区域和图像背景区域深度数值不同，因此使用深度阈值方式对手势图像展开滤波，手势图像深度数值表达公式如下

(1)

上述公式中，(i，j)表示手势图像深度点坐标，Depth(i，j)则表示该手势图像深度点坐标位置的深度数值，thr代表手势滤波过程中所设置的阈值，本文令阈值为900。利用式(1)计算得到的数值，使用图像积分方法实现手势图像滤波。

由于距离直方图内的深度值是相对距离数据，不由实际距离表达，因此需使用世界坐标的表达方式表示距离直方图内的深度图像从而获取其点云信息[7]。

令距离直方图内深度像素点为P，深度数值由draw表示，该像素点的坐标则由(i，j)表示，该像素点的深度滤波表达公式如下

d=Depth(i，j)·tan(draw)

(2)

将距离直方图内像素点的深度值转换为三维空间坐标，由(x，y，z)表示，其表达公式如下

(3)

上述公式中，b表示手势图像的宽度，h表示手势图像的高度。

利用式(2)与式(3)获取距离直方图内手势深度的点云信息。

2.1.2 图像曲面拟合

使用最小二乘方法对手势图像展开拟合，该方法在计算手势图像曲率时，单项式的曲面拟合基函数若符合线性无关条件则其表达手势信息更加全面与精准。曲面拟合表达式如下

(4)

上述式中，pi(x)、ai(x)分别表示拟合曲率的基函数和多项式系数向量，基函数所涵盖的单项式数量由n表示，拟合次数由T表示。

设置加权拟合误差能量表达式是计算基函数的多项式系数向量的首要条件，那么定义的加权拟合误差能量表达式如下

(5)

上述公式中，ω表示手势图像利用加权拟合误差能量函数完成曲面多点拟合后的图像深度数值[8]，本文利用高斯型加权函数，通过计算该函数驻点最低数值获取系数向量，而手势多点特征则为高斯曲率，高斯曲率表达公式如下

(6)

上述公式中，字母u的下角标x和y分别表示函数的一阶微分算子，xx和yy分别表示函数的二阶算子。通过计算手势图像的高斯曲率数值，利用高斯曲率绝对值描述手势图像内手指区域和手指弯曲情况。

由于手势图像的曲面构成较繁琐，无法完全的实现总体曲面拟合，为提升拟合精准度，最大限度表达手势图像多点特征，本文以区域拟合的方式进行手势图像多点拟合，以像素点方圆4*4厘米为一个拟合区域，进行多次拟合，从而保证较好地表达手势图像多点特征，为降低计算步骤，本文仅拟合手势存在区域，对于手势图像留白区域不展开计算[9]。

2.2 多点手势目标跟踪识别方法

利用KLT跟踪器跟踪手势图像多特征点，对手势目标展开跟踪，当手势图像内手势区域存在遮挡或在转换坐标时目标失踪，利用KLT跟踪器追踪手势图像多特征点可较好的解决此类问题。当手势区域完全被遮挡后，使用卡尔曼滤波器预测手势目标位置，使手势特征跟踪区间降低[10]，避免跟踪器引导信号中断情况，实现手势跟踪。

2.2.1 手势图像多特征点跟踪

KLT跟踪器在跟踪手势图像多特征点时，以手势图像某一帧图像内的可信度最高的特征点作为跟踪点，测量该跟踪点附近每帧图像的互相关数值，获取下一帧图像内该跟踪点区域，并计算上一帧图像与下一帧图像之间距离。

令W表示具有纹理特征的手势特征窗口，当时刻为t时，手势图像的图像帧为I(x，y，t)，当时刻为时t+τ，手势图像的图像帧则为I(x，y，t+τ)，由于图像亮度、时间连续和空间均具有相同特性，则图像帧表达公式如下

I(x，y，t)=I(x+gx，y+gy，t+τ)

(7)

上述公式中，点X(x，y)的位移变化由g=(gx，gy)表示。

令ε表示KLT跟踪器跟踪目标误差，通过计算跟踪目标误差最小位移g，令时刻为t时的手势图像特征窗口由I(X)表示，时刻为t+τ时的特征窗口由J(X)表示，则KLT跟踪器跟踪目标误差表达公式如下

(8)

上述公式中，A、g、ω(X)分别表示变形矩阵、平移向量、加权函数，利用微分方式获取KLT跟踪器跟踪目标误差最小数值，其简化后的表达式如下

Zg=e

(9)

其中

(10)

利用上述公式即可获取手势图像特征窗口位移数值，实现手势目标定位。

2.2.2 手势目标定位

利用手势图像多特征点在两帧图像内的坐标点位置，计算手势图像仿射变换矩阵，将手势图像区域内四边顶点坐标通过仿射变换矩阵方式计算与其相对坐标点，可重新判定手势图像区域[11]。

令(x，y)表示二维坐标点，仿射变换后的坐标由(x’，y’)表示，则仿射变换表达公式如下

(11)

令X=[x1，x2，…，xn]和Y=[y1，y2，…，yn]分别表示手势与其特征点集合，则特征点的仿射变换关系表达公式如下

yi=f(xi)=Nxi

(12)

上述公式中，N表示仿射变换矩阵，且i=1，2，…，n。

2.3 基于卡尔曼滤波器的多点手势识别

根据手势目标定位信息，利用卡尔曼滤波器实现多点手势位置识别，其依据上一帧手势图像位置和速度，识别下一帧手势图像位置[12]。令k表示图像帧，则在该帧内手势状态向量可表达为Uk=(cx(t)，cy(t)，vx(t)，vy(t))，cx(t)、cy(t)分别为手势的横向、纵向位置。vx(t)、vy(t)分别表示横向、纵向速度，当图像帧为k时，手势状态向量状态表达式如下

Uk=Bk-1Uk-1+wk-1

(13)

当图像帧为k时，手势状态向量观测表达式如下

Zk=HkUk+vk

(14)

上述公式中，Uk、Hk分别表示状态向量和观测矩阵，k-1时刻到k时刻时的状态转移矩阵由Bk表示，Zk、wk-1、vk分别为观测向量、状态噪声向量、观测噪声向量。

卡尔曼滤波器识别过程如下：

(15)

增益矩阵表达式如下

(16)

预测状态表达式如下

(17)

预测误差协方差矩阵表达式如下

(18)

当手势图像特征点被遮挡时，运行卡尔曼滤波器，依据手势图像两帧区间识别当前手势区间，利用上述步骤可实现人机交互时的多点手势识别。

3 实验分析

为验证本文方法实际效用，在某电视的人机交互VR游戏内仿真使用本文手势识别方法，仿真软件为MATLAB2020b仿真软件，通过仿真手势识别完成游戏限定人机交互任务。

3.1 图像处理效果测试

以手势图像滤波为手势特征提取前提，以图像滤波能力作为衡量其特征提取性能指标，测试本文方法手势图像特征提取性能，结果如图2所示。

图2 手势图像滤波测试结果

分析图2可知，手势与其图像背景的深度值处于不同区间，使用本文方法滤波后的手势图像背景呈白色，手势区域呈深灰色，其对比度明显，手势边缘轮廓清晰，由此可见，本文方法图像滤波能力强。

3.2 手势目标定位测试

以游戏过程中某10组手势坐标为实验对象，测试本文方法手势目标定位能力，为更加凸显本文方法使用效果，同时使用文献[3]方法和文献[4]方法展开测试，测试结果如表1所示。

表1 三种方法手势目标定位测试(cm)

分析表1可知，使用本文方法定位的手势坐标与游戏过程中的手势坐标完全相同，而文献[3]方法定位的手势坐标虽然y轴方向与仿真软件模拟完全相同，但x轴方向坐标出现两次错误，最大误差值为2.2cm，文献[4]方法定位的手势坐标在x轴方向出现一次错误，在y轴方向存在3次错误，综合而言，本文方法定位的手势目标最准确，可见其手势定位能力更好。

3.3 手势识别能力测试

以游戏过程中存在遮挡的100组手势图像为实验对象，利用协方差数值表达手势识别能力，测试三种方法手势识别能力，结果如图3所示。

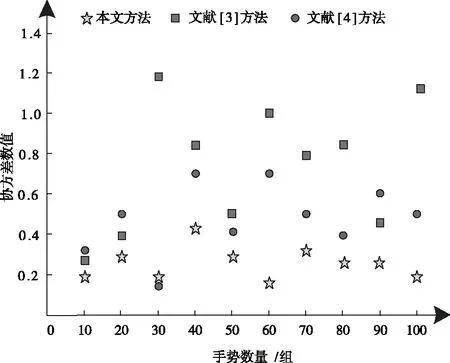
图3 三种方法手势识别协方差数值

分析图3可知，三种方法手势识别协方差数值保持上下波动状态，其中文献[3]方法的协方差数值最低为0.22，最高为1.2，二者差值为0.98，表明其协方差数值波动区间较大，而文献[4]方法和本文方法的协方差数值最高数值与最低数值之差分别为0.67和0.25。综合来看，本文方法的协方差波动区间最小，表明该方法识别人机交互过程的手势准确，具有较强手势识别能力。

4 结论

本文对人机交互多点手势识别展开仿真研究，在手势特征点跟踪过程中，引入卡尔曼滤波器，降低手势跟踪区域范围，实现手势跟踪。经过实验验证，本文方法滤波后的手势图对比度与手势边缘轮廓均清晰可见，特征提取能力好；定位的手势坐标与游戏过程中的手势坐标完全相同，定位能力强；手势识别时的协方差数值最高数值与最低数值之差仅为0.25，协方差波动区间小，人机交互多点手势识别能力优秀。