带凹槽结构的涡轮泵平衡活塞工作特性分析

党枭睿，许开富，金 路，黄锡龙

(西安航天动力研究所，陕西 西安 710100)

0 引言

涡轮泵转子系统转速高，且转子系统剩余轴向力由轴承承受，故大推力液体火箭发动机涡轮泵中均设置单独的轴向力平衡系统，以防止轴承受力过大。涡轮泵的不平衡轴向力、产品的制造偏差、系统的调节偏差，均会随尺寸和工作压力的增大而逐渐增大，发动机变工况、起动、关机时，涡轮泵中均产生很大的轴向力冲击。实践证明，轴向力平衡系统的稳定性和可靠性直接决定了涡轮泵的工作可靠性。因此，各国对轴向力平衡技术均开展了大量理论和试验研究，解决了涡轮泵研制中的轴向力问题。其中，用途最广、效果最好的解决方法之一就是在涡轮泵中增设平衡活塞结构。

平衡活塞是一种自动卸荷装置，当转子在轴向力的作用下产生位移时，平衡活塞的高、低压轴向间隙就发生变化，导致平衡腔内的压力分布产生变化，从而使转子上的轴向力达到平衡状态。

某型泵在设计时对平衡活塞结构加入了消旋整流装置以平衡过大的轴向力。消旋整流装置可用于平衡轴向力是由Kurokawa在1994年研究各旋转过流部件压力分布与实测值的吻合情况时发现的，研究发现安装在主离心叶轮前壳体壁面上的消旋整流装置降低了径向压降，增大了指向出口的轴向力，使总轴向力幅值明显降低，一般认为深度为0.5 mm的径向槽能显著降低压降，而深度为1 mm的径向槽能使压力分布几乎均匀。

Shimura等以LE-7涡轮氧泵为研究对象，得出两个结论：首先，平衡腔进口轴向间隙太小则无法确保涡轮泵运行安全；其次，离心叶轮后盖板入口通流引起的角动量明显增加了间隙腔体内径向压降。Shimura等采用考虑边界层条件和腔体角动量变化影响的内流系统分析计算方法对带螺栓槽的涡轮泵内部流路系统开展分析，结果表明该系统具有较宽的自平衡范围，适用于火箭涡轮泵。Kimura等在2011年对离心叶轮与围带间隙内的泄漏流动进行了数值模拟，结果表明径向压差的减小是由消旋整流装置内部形成的复杂涡流结构和泄漏流在外部区域迅速失去角动量引起的。

Matsui等通过实验和数值模拟分析了J型槽附近的流场分布和其对轴向力的影响。结果表明，在适当的槽形结构下，最佳效率点的轴向力可减小38%左右，而扬程系数等其他性能则完全不受影响。

综上所述，日本航天结构以LE-7涡轮氧泵为研究对象，初步揭示了凹槽结构消旋整流的作用机理，并通过数值计算和试验测试对上述结论进行了充分验证，此后，韩国在研制产品过程中，对该结构进行了充分借鉴。本文对带不同凹槽结构的平衡活塞后泄漏流道模型进行了数值仿真，对平衡活塞后泄漏流道中压力分布情况，凹槽结构消旋整流、消除径向压降、降低轴向力的机理进行了更加深入的研究，指出了凹槽结构中对平衡轴向力起主要作用的部分，分析了轴向力和泄漏流量对于凹槽宽度和深度变化的敏感度，为凹槽结构的进一步优化设计提供了参考。

1 仿真模型

1.1 物理模型

图1为涡轮泵双平衡间隙的平衡活塞装置，当轴向力过大时，该装置通过调节低压轴向间隙和高压轴向间隙的宽度来改变平衡腔内压力分布。本文的研究对象即平衡活塞后泄漏流道部分已在图中标出。

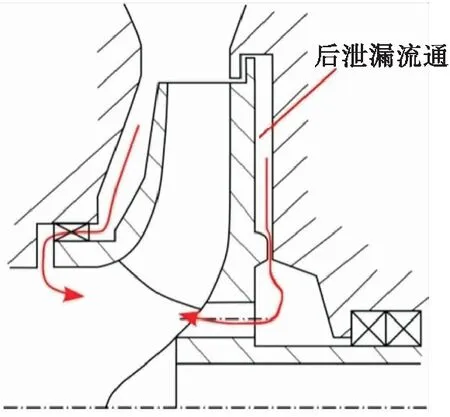
图1 双平衡间隙平衡活塞系统Fig.1 A balanced piston system with two balance gaps

为简化模型结构、节省计算时间和计算资源，对带不同凹槽结构的平衡活塞后泄漏流道的1/19进行仿真，如图2所示，该图为从壳体外部方向观察的正视图。下面对图2中的6种平衡活塞后泄漏流道进行具体介绍。

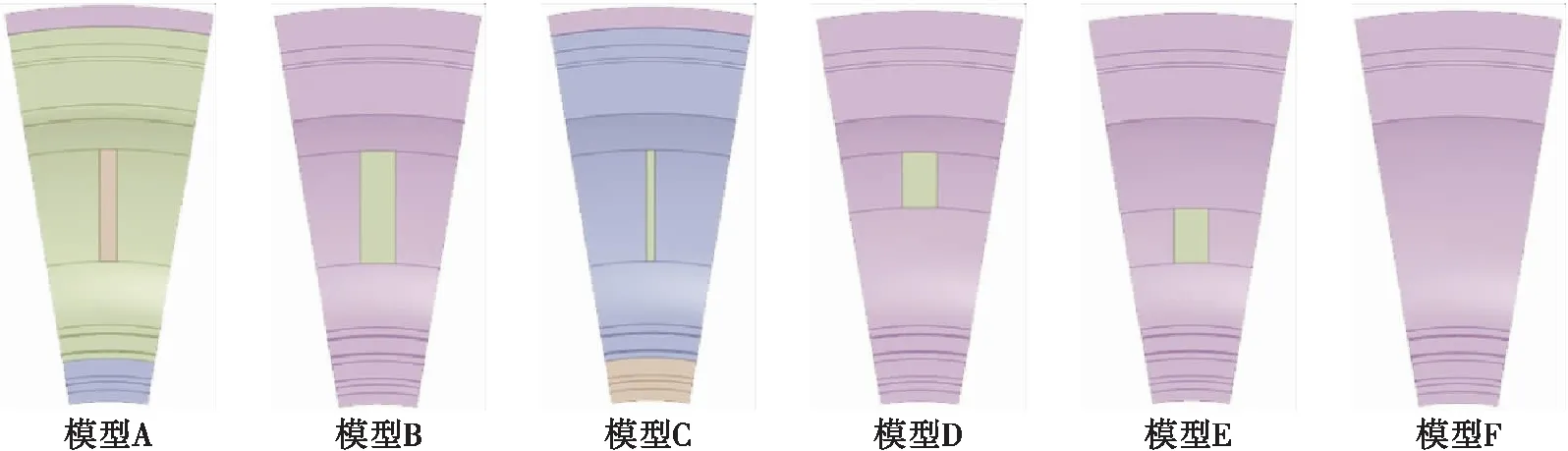
图2 各仿真模型对比图Fig.2 Comparison of each simulation model

模型A为试验装置的平衡活塞后泄漏流道模型；初步研究结果表明，凹槽的宽度变化对平衡活塞结构消旋整流效果的影响较为明显，为对不同宽度凹槽的消旋整流机理做进一步研究，将凹槽结构的宽度改为基础模型的2倍和1/2，凹槽宽度为初始凹槽结构2倍的模型称为模型B，凹槽宽度为初始凹槽结构1/2的模型称为模型C。模型F则是不带凹槽结构的平衡活塞后泄漏流道模型。

此外，为分别研究凹槽结构上半部分和下半部分的消旋整流作用，建立只保留模型B凹槽结构的上半部分的新模型，称为模型D；只保留模型B凹槽结构的下半部分的新模型，称为模型E。

1.2 计算模型

首先，对某型泵的全尺寸流道进行数值仿真。仿真模型包含入口域、诱导轮域、离心轮域、扩压器域、蜗壳域、前后泄漏域以及出口管道流域。延长泵入口及出口管道，消除进出口边界扰动的影响。

对各流域进行六面体网格划分。对各壁面处网格进行加密，使得各壁面值满足要求，在进行网格无关性验证后利用ANSYS CFX进行数值求解。采用RANS方法进行稳态求解，湍流模型选用SST-模型，壁面处采用Automatic Wall Function算法进行处理，动静耦合界面采用Frozen Rotor模型进行数据传递，收敛精度设置为1×10。

得到全流场仿真结果后，提取平衡活塞后泄漏流道径向压力随半径变化图，与水试试验数据对比，如图3所示。观察图3可知，此仿真结果的误差在可接受范围内。为对平衡活塞后泄漏流道的流体流动进行深入研究，从该数值仿真结果中提取出平衡活塞后泄漏流道模型、后泄漏流道的进口压力、进口速度方向及出口压力，进行更精确的局部数值仿真。

图3 全流场仿真与试验数据对比图Fig.3 Comparison of full flow field simulation and test data

进一步对离心叶轮后盖板与壳体之间泄漏流进行数值模拟，模型文件如图2所示。利用ANSYS MESH软件对其进行六面体网格划分，图4为模型A网格示意图和最小截面位置处网格局部放大图。对壁面区域处网格进行加密，使得各壁面平均值小于10，以满足计算要求并且能够尽可能捕捉到流场细节。

图4 模型A网格示意图和局部网格放大图Fig.4 Schematic diagram and partial enlarged view of grid for model A

采用5套不同网格进行网格无关性验证，寻找合适的网格密度，结果如表1所示。为在算力允许的范围内更为准确地捕捉流场细节，选取方案4的网格进行仿真计算。

表1 网格无关性参数

各模型内侧面为旋转面，转速为6 000 r/min，外侧面为固定面。流体介质为水，温度为20 ℃，其余性质为水在20 ℃下的物理性质。为消除进出口边界扰动的影响，同样将泵入口及出口管道沿直线延长管道水力直径的4倍距离。

2 仿真结果分析

2.1 径向压力分布分析

图5为各模型径向压力分布图。按照压力分布情况，可将其分为两组：Ⅰ 组包括无凹槽结构的模型F、凹槽宽度为初始模型1/2的模型C和仅有下半部分凹槽结构的模型E，图中用红色线画出；Ⅱ 组包括初始模型A、凹槽宽度为初始模型2倍的模型B和仅有上半部分凹槽结构的模型D，图中用蓝色线画出。

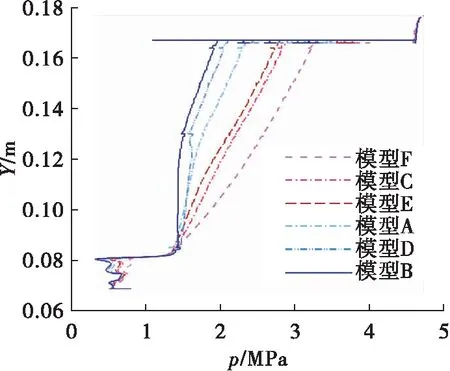
图5 各模型径向压力分布Fig.5 Radial pressure distribution of each model

观察图5可知：Ⅰ组各模型在转静空腔中的压力降低速度较均匀，且模型C、E各位置压力大小都低于无凹槽结构的模型F。Ⅱ组模型几乎没有消除径向压降和降低轴向力的效果。Ⅱ组各模型的压降主要集中在迷宫密封部分，流至转静空腔入口处的流体压力已降至较低水平。而对于转静空腔内部的流动，其前半部分压力降低速度较快，后半部分压力则趋于平稳。此外，由图5还可以看出，模型B各点压力最低，消除径向压降和降低轴向力效果最好，但降低轴向力效果越好的模型，其泄漏流量越大，设计时应考虑此因素影响。

将泄漏流道整体考虑为一段管路，可用以下流阻公式解释泄漏流量的变化原因。

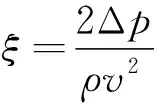
(1)

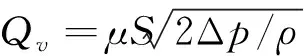
(2)

式中为流体流速。

取模型B和模型F进行对比分析，模型B的入口平均轴向流速为1.72 m/s，出口平均轴向流速为7.61 m/s；模型F的入口平均轴向流速为1.13 m/s,出口平均轴向流速为4.99 m/s，可以看出，模型B中流体沿平衡活塞后泄漏流道向内流动的平均速度远大于模型F。

由式(1)可知，在压降和流体密度不变的情况下，流体速度增加，流体阻力系数降低。阻力系数降低则会导致流量系数增加。由式(2)可知，流量系数增加，在其他参数都不变的情况下泄漏流量也随之增加。

对迷宫密封部分运用式(2)，可解释Ⅱ组各模型的压降主要集中在迷宫密封部分的原因。迷宫密封处于平衡活塞后泄漏流道前段，模型B相对模型F而言，其迷宫密封内流体平均流速变化较小，故迷宫密封部分的流阻系数和流量系数变化较小。泄漏流量增大，流量系数、通道截面积、流体密度不变，压降Δ增大。这与前文得出的结论是相符的。

2.2 流动机理分析

为便于分析凹槽结构消旋整流机理，取消除径向压降和消除轴向力效果最好的模型B进行分析。图6和图7分别为模型B壳体壁面流线图和压力分布图。由图6可以看出，流体自右上流入凹槽结构后，部分向左上进行回流，另一部分流体和左侧回流汇合，形成向下和向右的流线。汇合后的流体被限制在凹槽内部流动，故其切向速度降低，径向速度升高，总速度升高，压力降低，从而在凹槽结构的右下部分形成低压区，在凹槽和壁面左上和右上接触区形成逆压区，如图7所示。

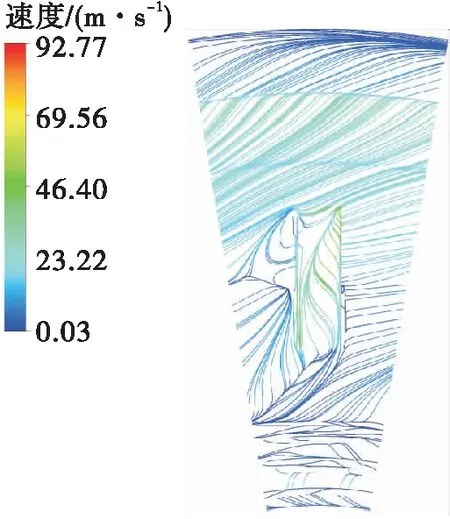
图6 模型B壳体壁面流线Fig.6 Wall streamline of model B

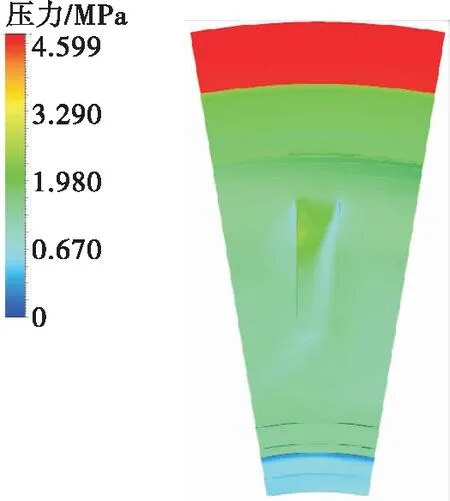
图7 模型B壳体壁面压力分布Fig.7 Wall pressure distribution of model B

根据模型B径向压力分布和流体流速的明显不同，将流动从凹槽中心，即=0.13 m处将转静空腔分为上半部分和下半部分。

此外，分析图5～图7，还可得出凹槽结构降低轴向力的具体机理。凹槽外部流体自右上而来，不受凹槽结构影响，故转静空腔上半部分的压力降低速度未受明显影响。而流至凹槽内部的流体，流线被向下引导，其切向速度降低，径向速度升高，升高后的径向速度被离心力抵消一部分，使得从凹槽结构内部流至外部的流体角动量和流速明显降低。

根据上述分析并结合文献[16-21]，得出

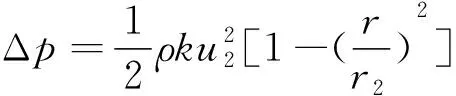
(3)

式中：为流体切向速度与旋转面切向速度之比，即旋流比；为转静空腔顶部半径；为转静空腔底部半径；为旋转面在转静空腔顶部的切向速度。

角动量和流速的降低使凹槽外部即转静空腔下半部分的旋流比降低，则径向压差Δ降低。这也与图5中模型B的径向压力分布相符。由2.1节可知，模型B的主要压降都集中在了迷宫密封部分，流至转静空腔的流体压力已降至较低水平，且转静空腔上半部分压力随半径缓慢降低，下半部分压力趋于平稳，故转静空腔内部形成大面积低压区，有效降低了其轴向力的大小。

图8、图9分别为仅有上半部分凹槽结构的模型D和仅有下半部分凹槽结构的模型E的流线图。观察图5、图8、图9，可知上半部分凹槽结构在降低轴向力方面起主要作用。

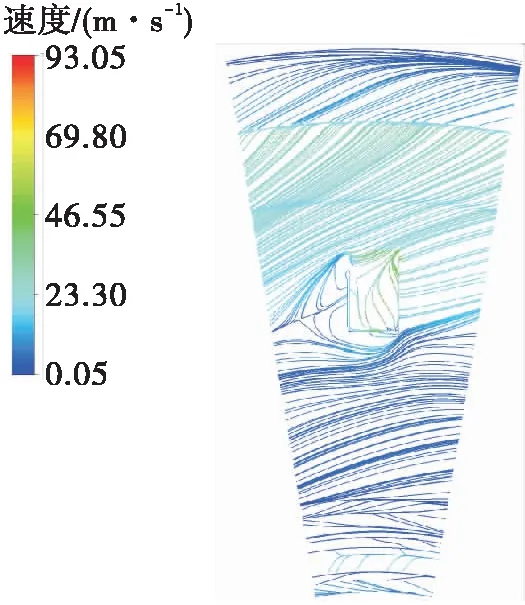
图8 模型D壳体壁面流线Fig.8 Wall streamline of model D

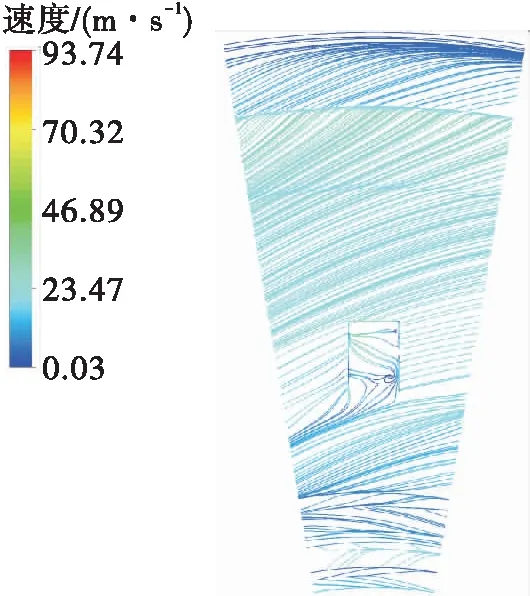
图9 模型E壳体壁面流线Fig.9 Wall streamline of model E

由图8可以看出，流体在上半部分凹槽结构内形成和完整凹槽结构相似的涡旋结构，有效降低了转静空腔下半部分流体角动量和流速，进而消除转静空腔下半部分的径向压降，降低转静空腔内压力大小，达到降低轴向力的目的。而只存在下半部分凹槽结构的模型E消旋整流效果较差，由图9可以看出，其凹槽结构内未出现明显的涡旋结构，流体流速和流动方向都未出现明显变化，其流线与无凹槽结构模型F相似，流速和角动量分布相比模型F也未出现明显变化。

2.3 敏感性分析

为进一步研究轴向力和泄漏流量对于凹槽宽度和深度变化的敏感度，将模型B凹槽结构的宽度减少0.5 mm、1 mm，增加0.5 mm、1 mm；将模型B凹槽结构的深度减少0.5 mm、1 mm，增加0.5 mm、1 mm，进行进一步仿真计算。

图10为轴向力大小随凹槽结构宽度和深度的变化图，图11为泄漏流量随凹槽宽度和深度的变化图。可以看出，凹槽宽度的微小变化就会导致轴向力和泄漏流量的大幅变化，而凹槽深度则对轴向力和泄漏流量的影响较小。在一定范围内，轴向力、泄漏流量和凹槽宽度、深度都基本呈线性关系，轴向力大小和泄漏流量大小则呈负相关，这与前文分析也是相符的。

图10 轴向力对凹槽深度、宽度的敏感度Fig.10 Sensitivity of axial force to groove depth and width

图11 泄漏流量对凹槽深度、宽度的敏感度Fig.11 Sensitivity of leakage flow to groove depth and width

观察各模型流线图可知，凹槽内部流体主要由两部分组成：撞击到凹槽结构左壁面后向右下方回流的流体和自右上而来向凹槽右下方流动的流体。在凹槽宽度较小时，槽内流体主要由撞击到凹槽结构左壁面后向右下方回流的流体组成，如图12所示。随着凹槽宽度的增加，自右上而来向凹槽右下方流动的流体占比逐渐增多，如图6所示。

图12 模型C壳体壁面流线Fig.12 Wall streamline of model C

自右上而来向凹槽右下方流动的流体流线较柔和，和凹槽壁面撞击次数较少，即流动损失较小。在凹槽宽度增大的基础上，流动损失降低，故从较宽凹槽内流出的流体对主流产生的影响也较大，其流量和径向速度都较大，切向速度较低，故凹槽下部流体的旋流比随着凹槽宽度的增加而降低。由2.2节可知，旋流比降低，其径向压差降低，轴向力大小也降低。而凹槽深度的变化对槽内流体流动无明显影响，对泄漏流量和主流流速影响也相对较小。

3 结论

本文利用试验数据对某型泵全流场数值仿真结果的准确性进行验证，通过全流场数值仿真得到了平衡活塞后泄漏流道出入口流动、压力参数。利用此参数在CFX内对多种凹槽结构进行更精确的平衡活塞后泄漏流道数值仿真，对带凹槽结构的平衡活塞后泄漏流道进行了压力分布分析、流动机理分析和敏感性分析,得到了以下结论：

1)凹槽结构使平衡活塞后泄漏流道的总流阻降低，总泄漏流量增加。但迷宫密封流阻不变，转静空腔流阻降低，故迷宫密封处的压降升高，转静空腔处的压降降低。

2)凹槽外部流体和凹槽结构相互碰撞，流速降低；凹槽内部的流体被凹槽结构限制，切向速度大幅降低，径向速度升高，升高后的径向速度被离心力部分抵消，凹槽结构内形成复杂涡旋。流经凹槽结构的流体角动量和切向流速都大幅降低，从而旋流比降低，径向压差降低。因迷宫密封处压降高，转静空腔内径向压差低，故转静空腔内压力稳定在较低水平，轴向力降低。

3)凹槽结构上半部分对于降低压力和轴向力起主要作用。流体在上半部分凹槽结构内形成和完整凹槽结构相似的涡旋结构，有效降低了流至转静空腔下半部分流体的角动量和流速，进而降低转静空腔下半部分的径向压降和分布压力，达到降低轴向力的目的。

4)轴向力对凹槽宽度变化十分敏感，而对于凹槽深度变化不敏感。有以下两方面原因：凹槽宽度增加直接增大了槽内流出的流体流量，增大了槽内流体对主流影响；随着凹槽宽度增加，流体在槽内流动的平均损失降低，径向速度增加，切向速度降低。凹槽下部主流的角动量和切向流速都大幅降低，从而径向压差降低，转静空腔内压力降低，轴向力降低。