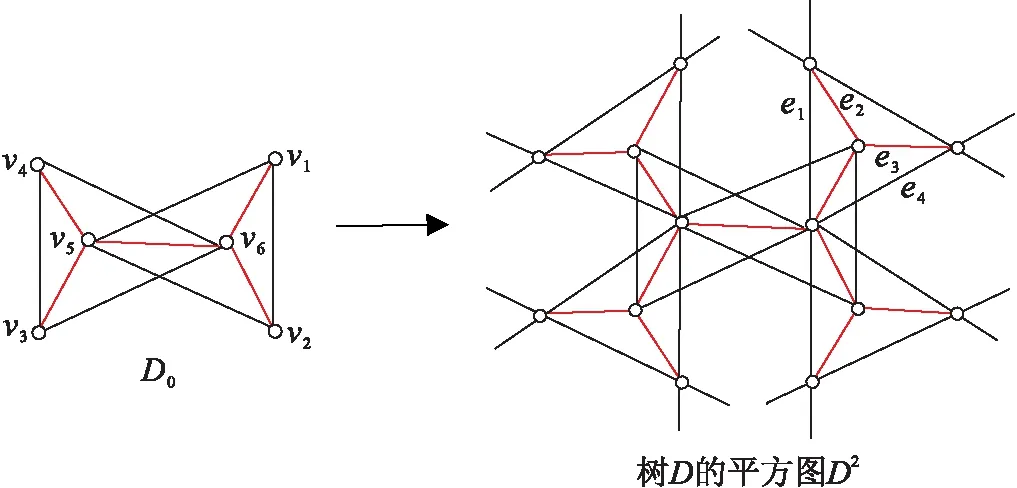
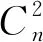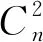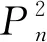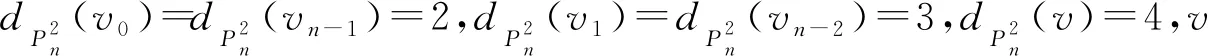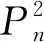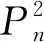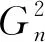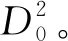平方图的邻点全和可区别全染色

王 芹, 杨 超*, 常景智, 程银万, 姚 兵

(1. 上海工程技术大学数理与统计学院, 智能计算与应用统计研究中心, 上海 201620;2. 西北师范大学数学与统计学院, 兰州 730070)

图的染色理论在离散系统、组合分析和网络通讯等领域有着广泛的应用,具体涉及时间表问题、排序问题、排课表问题、存储问题、电路安排和任务分配等。由于其重要的理论意义和广泛的应用价值,染色问题一直是学者们关注和研究的热点。

在图的邻点被扩展和可区别全染色的基础上, FLANDRIN等[11]进一步定义了图的邻点全和可区别非正常全染色,但并未对图的邻点全和可区别非正常全染色问题进行深入探究,仅仅把图的邻点全和可区别非正常全染色与邻点被扩展和可区别全染色作了一个简单的比较。基于此,本文将深入探讨路、圈、毛毛虫、广义星以及最大度为 3 且不包含 2 度点的树的平方图的邻点全和可区别非正常全染色问题。

1 预备知识

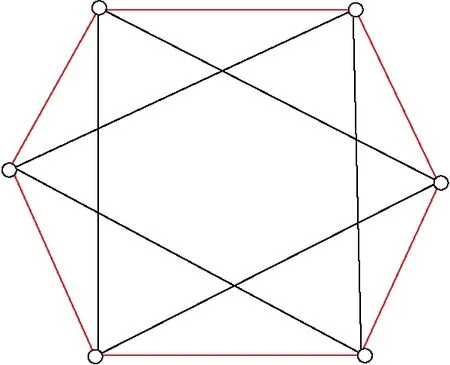
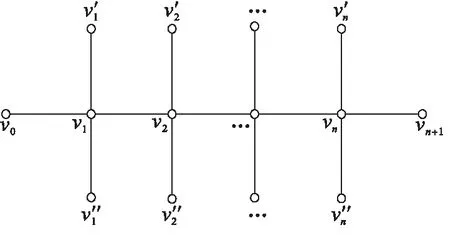
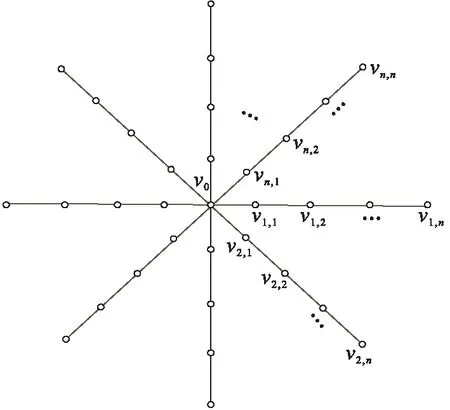
本文论及的图G均为无向简单图,用V(G)、E(G)分别表示G的顶点集、边集。符号[s,t]表示非负整数集{s,s+1,s+2,…,t},其中s和t均为整数,且满足0≤s

设u、v为图G中任意两点,distG(u,v)表示连接u、v两点间的最短路的长度。图G的平方图G2是以V(G)作为它的点集,2个点u、v在G2中相邻当且仅当1≤distG(u,v)≤2。圈C6的平方图如图1所示。容易验证,星、轮和完全r-部图(r≥2)的平方图均为完全图。

图1 圈C6的平方图

下面给出 2 类特殊树的定义。

定义2设图G的点集V(G)={v0,vn+1,vi,v′i,v″i|i[1,n]}, 边集E(G)={viv′i,viv″i,vivi+1,v0v1|i[1,n]},则称图G为毛毛虫。

毛毛虫示意图见图 2。由定义 2 知,dG(v0)=dG(v′i)=dG(v″i)=dG(vn+1)=1,dG(vi)=4,i[1,n]。当n=1时,|G|=5,此时毛毛虫G的平方图是完全图K5,即G2=K5。

图2 毛毛虫

定义3设图S的点集V(S)={v0,vi,j|i[1,n],j[1,h]},边集E(S)={v0vi,1,vi,j-1vi,j|i[1,n],j[2,h]},则称图S为广义星(图3)。

图3 广义星

2 主要结果

f1(v4i-4v4i-3)=1,f1(v4i-3v4i-2)=1,f1(v4i-2v4i-1)=1,f1(v4i-1v4i)=2,i[1,n];f1(v2 iv2 i+2)=1,f1(v2 i+1v2 i+3)=2,i[0,n]。

由染色f1可得：φ(v4i)=10,φ(v4 i+1)=11,φ(v4 i+2)=9,φ(v4i+3)=12,i[0,n]。则f1为的一个邻和可区别非正常 2- 边染色。

f2(v0v1)=f2(v4v5)=1,f2(v1v2)=f2(v2v3)=f2(v3v4)=f2(v5v6)=f2(v6v7)=2;f2(v4i-1v4i)=f2(v4iv4i+1)=f2(v4i+1v4i+2)=1,f2(v4i+2v4i+3)=2,i[2,n];f2(v0v2)=1,f2(v1v3)=2,f2(v2v4)=1,f2(v3v5)=2,f2(v4v6)=f2(v5v7)=1,f2(v6v8)=2;f2(v2i-1v2i+1)=1,f2(v2iv2i+2)=2,i[4,n]。

由染色f2可得:φ(v0)=9,φ(v1)=12,φ(v2)=11,φ(v3)=13,φ(v4)=10,φ(v5)=11,φ(v6)=12,φ(v7)=10,φ(v8)=11,φ(v4i-3)=9,φ(v4i-2)=12,φ(v4i-1)=10,φ(v4i)=11,i[3,n]。则f2为的一个邻和可区别非正常2-边染色。

f3(v4 iv4 i+1)=f3(v4 i+1v4 i+2)=f3(v4 i+2v4 i+3)=1,f3(v4 i+3v4 i+4)=

f3(vn-2vn-1)=2,f3(vn-1v0)=2,f3(v2 iv2 i+2)=1,f3(v2 i+1v2 i+3)=2,i[0,n]。

由染色f3可得:φ(v4 i)=10,φ(v4 i+1)=11,φ(v4 i+2)=9,φ(v4 i+3)=12,φ(vn-2)=11,φ(vn-1)=13,i[0,n]。则f3为的一个邻和可区别非正常 2-边染色。

f4(v0v1)=1,f4(v1v2)=f4(v3v4)=2,f4(v2v3)=1;f4(v4iv4i+1)=2,f4(v4i+1v4i+2)=f4(v4i+2v4i+3)=f4(v4i+3v4i+4)=1,i[1,n];f4(v0v2)=f4(v2v4)=1,f4(v1v3)=2;f4(v2i-1v2i+1)=1,f4(v2iv2i+2)=2,i[2,n]。

由染色f4可得:φ(v0)=9,φ(v1)=12,φ(v2)=10,φ(v3)=11,φ(v4)=12,φ(v5)=10,φ(v6)=11,φ(v4i-1)=9,φ(v4i)=12,φ(v4i+1)=10,φ(v4i+2)=11,i[2,n]。则f4为的一个邻和可区别非正常 2-边染色。

f1(v0v1)=1,f1(v1v2)=2,f1(v0v2)=1;f1(v3i-1v3i)=f1(v3 iv3 i+1)=2,f1(v3 i+1v3 i+2)=f1(v3 i-1v3 i+1)= 1,f1(v3 iv3 i+2)=2,f1(v3 i-2v3 i)=1,i[1,n]。

由染色f1可得:φ(v0)=5,φ(v1)=8,φ(v3 i+1)=10,φ(v3i-1)=11,φ(v3i)=12,φ(vn-2)=8,φ(vn-1)=6,i[1,n]。 则f1为的一个邻和可区别非正常 2-边染色。

f2(v0v1)=1,f2(v1v2)=2,f2(v0v2)=1,f2(v3i-1v3i)=f2(v3 iv3 i+1)=2,f2(v3 i+1v3 i+2)=f2(v3 i-1v3 i+1)=1,f2(v3iv3i+2)=2,f2(v3i-2v3i)=f2(vn-2vn-1)=1,i[1,n]。

由染色f2可得:φ(v0)=5,φ(v1)=8,φ(v3i+1)=10,φ(v3i-1)=11,φ(v3i)=12,φ(vn-2)=8,φ(vn-1)=5,i[1,n],则f2为的一个邻和可区别非正常2-边染色。

定理3设G为阶数为n的毛毛虫。若n=5, 则 fgndi∑(G2)=3;若n>5,则 fgndi∑(G2)=2。

证明设G为阶数为n的毛毛虫,G2如图 4 所示。若n=5,则G2=K5，容易验证fgndi∑(G2)=fgndi∑(K5)=3。以下考虑n>5的情形。由定义2知,dG2(v0)=dG2(vn+1)=dG2(v′i)=dG2(v″i)=4,dG2(v1)=dG2(vn)=7,dG2(vi)=10,i[2,n-1]。若G2的所有点和边均染颜色 1,则φ(v0)=φ(vn+1)=φ(v′i)=φ(v″i)=9,φ(v1)=φ(vn)=15,φ(vi)=21,i[2,n-1],矛盾。故G2的一个邻和可区别非正常全染色至少需 2 种颜色,不妨用颜色 1 和颜色 2 对G2进行非正常全染色且顶点全部染颜色 1。则φ(v0)、φ(vn+1)、φ(v′i)、φ(v″i)均不超过13,且φ(v1),φ(vn)≥15, 但φ(vi)≥21,i[2,n]。故φ(vi){φ(v0),φ(vn+1),φ(v′i),φ(v″i),φ(v1),φ(vn)}。 故按上述染色方案,若要证G2存在一个邻和可区别非正常2-全染色,则仅需证G2存在一个邻和可区别非正常 2-边染色。

图4 毛毛虫的平方图

下面分2种情况对G2的边进行染色。

情形1.n≡0(mod 3)。定义G2的一个2-边染色f1如下:

f1(v″3i-2v3i-1)=f1(v″3i-1v3i)=1,f1(v″3iv3i+1)=2,i[1,n],

剩余其他边全部染颜色1。

由染色f1可得,φ(v0)=10,φ(v1)=17,φ(v3i-1)=22,φ(v3i)=23,φ(v3i+1)=24,φ(vn)=16,φ(vn+1)=10,φ(v′i)=9,φ(v″i)=11,则f1为G2的一个邻和可区别非正常 2-边染色。

f2(v″3iv3i+1)=f2(v″nvn+1)=2,i[1,n],

其余边全部染颜色1。

由染色f2可得,φ(v0)=10,φ(v1)=17,φ(v3i-1)=22,φ(v3i)=23,φ(v3i+1)=24,φ(vn)=15,φ(vn+1)=10,φ(v″i)=11,φ(v′i)=9,则f2为G2的一个邻和可区别非正常 2-边染色。

定理4设S是广义星,则fgndi∑(S2)=2。

证明设S1,n=(V(S1,n),E(S1,n))为一个星,其中，V(S1,n)={v0,vi,1|i[1,n]},E(S1,n)={v0vi,1,v0vi,2|i[1,n]}。为叙述方便,称S1,n为广义星平方图S2中的一个星结构。设v0连接n条长为h的路,它们的点集记为{vi,1,vi,2,vi,3,…,vi,h|i[1,n]},边集记为{vi,1vi,2,vi,2vi,3,vi,3vi,4,…,vi,h-1vi,h,vi,1vi,3,vi,2vi,4,vi,3vi,5,…,vi,h-2vi,h|i[1,n]}。

广义星平方图S2如图 5 所示。下面对星结构进行染色。将星结构分为 2 个部分:下标i[1,「(n-1/2)⎤]的部分记为A,下标i[「(n-1/2)⎤+1,n]的部分记为B。令与v0相连的边全部染颜色2,则φ(v0)=6n+1。令f(vi,1vn,1)=1,i[1,n-1];f(vi,1vn-1,1)=1,i[2,n-2];f(vi,1vn-2,1)=1,i在A中令f(vi,1vi,2)=2(i[1,「(n-1)/2⎤]),在B中令f(vi,1vi,2)=1(i[「(n-1)/2⎤+1,n]),则星结构上点的权重从vi,1开始以公差为1逐渐递减,且权重区间为[3n+6,2n+7]。

图5 广义星的平方图

下面对A中的路PA进行染色。

情形 1.h≡0(mod 3)。定义PA的一个2-边染色f1如下:

f1(vi,2vi,3)=f1(vi,h-1vi,h)=1;f1(vi,3 j-1vi,3 j)=2,j[2,h];

f1(vi,3jvi,3j+1)=f1(vi,3jvi,3j+2)=f1(vi,3j+1vi,3j+3)=1,

f1(vi,3j-1vi,3j+1)=f1(vi,3j+1vi,3j+2)=2,j[1,h]。

由染色f1可得:φ(vi,3j-1)=12,φ(vi,3j)=10,φ(vi,3j+1)=11；φ(vi,h-1)=8,φ(vi,h)=5,j[1,h]。则f1为S2的一个邻和可区别非正常 2- 边染色。

情形 2.h≡2(mod 3)。定义PA的一个2-边染色f2如下:

f2(vi,2vi,3)=f2(vi,h-1vi,h)=f2(vi,h-2vi,h)=1,f2(vi,2vi,4)=2;f2(vi,3jvi,3j+1)=f2(vi,3jvi,3j+2)=f2(vi,3j+1vi,3j+3)=1,f2(vi,3j+1vi,3j+2)=f2(vi,3j+2vi,3j+3)=f2(vi,3j+2vi,3j+4)=2,j[1,h]。

由染色f2可得:φ(vi,3j-1)=12,φ(vi,3j)=10,φ(vi,3j+1)=11,φ(vi,h-1)=8,φ(vi,h)=5,j[1,h]。则f2为S2的一个邻和可区别非正常 2- 边染色。

情形 3.h≡1(mod 3)。定义PA的一个2-边染色f3如下:

f3(vi,2vi,3)=1,f3(vi,2vi,4)=2;f3(vi,3 j-1vi,3 j)=2,j[2,h];f3(vi,3jvi,3j+1)=f3(vi,3jvi,3j+2)=f3(vi,3j+1vi,3j+3)=1,f3(vi,3 j-2vi,3 j-1)=2,j[2,h];f3(vi,3 j+2vi,3 j+4)=2,j[1,h]。

由染色f3可得:φ(vi,3 j-1)=12,φ(vi,3 j)=10,φ(vi,3 j+1)=11,φ(vi,n-1)=8,φ(vi,n)=6,j[1,h]。则f3为S2的一个邻和可区别非正常 2- 边染色。

下面对B中的路PB进行染色。

情形 1.h≡0(mod 3)。定义PB的一个2-边染色g1如下:

g1(vi,2vi,3)=g1(vi,3vi,4)=g1(vi,3vi,5)=2,g1(vi,4vi,5)=g1(vi,h-1vi,h)=1;g1(vi,3jvi,3j+1)=g1(vi,3jvi,3j+2)=1,g1(vi,3 j+1vi,3 j+2)=2,j[2,h];g1(vi,3 j-1vi,3 j)=g1(vi,3 j-1vi,3 j+1)=2,g1(vi,3j+1vi,3j+3)=1,j[1,h]。

由染色g1可得：φ(vi,2)=12,φ(vi,3)=13,φ(vi,4)=11,φ(vi,3j-1)=12,φ(vi,3j)=10,φ(vi,3j+1)=11,φ(vi,h-1)=8,φ(vi,h)=5,j[2,h]。则g1为S2的一个邻和可区别非正常 2- 边染色。

情形 2.h≡2(mod 3)。定义PB的一个2-边染色g2如下:

g2(vi,2vi,3)=g2(vi,3vi,4)=g2(vi,3vi,5)=2,g2(vi,4vi,5)=1,g2(vi,h-1vi,h)=1;g2(vi,3j-1vi,3j)=g2(vi,3j-1vi,3j+1)=2,g2(vi,3 j-2vi,3 j)=1,j[1,h];g2(vi,3 jvi,3 j+1)=g2(vi,3 jvi,3 j+2)=1,g2(vi,3j+1vi,3j+2)=2,j[2,h]。

由染色g2可得：φ(vi,2)=12,φ(vi,3)=13,φ(vi,4)=11;φ(vi,3j-1)=12,φ(vi,3j)=10,j[2,h];φ(vi,3j+1)=11,φ(vi,h-1)=8,φ(vi,h)=5,j[2,h]。则g2为S2的一个邻和可区别非正常 2- 边染色。

情形 3.h≡1(mod 3)。定义PB的一个2-边染色g3如下:

g3(vi,2vi,3)=g3(vi,3vi,4)=2,g3(vi,4vi,5)=1,g3(vi,2vi,4)=g3(vi,3vi,5)=2;g3(vi,3 jvi,3 j+1)=g3(vi,3 jvi,3 j+2)=1,g3(vi,3 j+1vi,3 j+2)=2,j[2,h];g3(vi,3 j+2vi,3 j+3)=g3(vi,3 j+2vi,3 j+4) = 2;g3(vi,3 j+1vi,3 j+3)=1,j[1,h]。

由染色g3可得:φ(vi,2)=12,φ(vi,3)=13,φ(vi,4)=11,φ(vi,3j-1)=12,φ(vi,3j)=10,φ(vi,3j+1)=11,φ(vi,h-1)=8,φ(vi,h)=6,j[2,h]。则g3为S2的一个邻和可区别非正常 2-边染色。

基于染色fi和gi(i[1,3])可得,广义星平方图S2中存在一个邻点全和可区别非正常2-全染色。

定理5设D为最大度为3的树且D中无2度点。若D2=K4,则fgndi∑(D2)=3;若D2≠K4,则fgndi∑(D2)=2。

接下来考虑D2的染色。由树D的构造过程知, 当树D每递归一次,D2中对应增加 2 个新点和 5 条新边。首先把连接2个 3 度点的那条新边和2个新点都染颜色1,其余4条新边记为e1、e2、e3、e4(具体对应边如图6所示),(f(e1),f(e2),f(e3),f(e4))可能的染色方案(EC)如下:(C1)(1,2,1,1);(C2)(2,2,1,1);(C3)(2,2,1,2);(C4)(1,1,1,2)。按上述染色方案,要证D2存在一个邻和可区别非正常 2-全染色,仅需证D2存在一个邻和可区别非正常2-边染色。通过对树平方图D2的3度点w进行加点加边处理,点w的度由原来的3度增加为5度,与点w相邻的5度点则增加为7度点，与点w相邻的7度点则变为9度点。不妨记vm、vn、vs、vt分别表示度为3、5、7、9的点。按照上述染色方案(EC),得φ(vt)[19,26],φ(vs)[15,20],则φ(vn)max=14 <φ(vs)min=15。因为树平方图中最多有4个度为 9 的点相邻,所以可取φ(vt)[21,24],则φ(vs)max=20<φ(vt)min=21。通过上述讨论,度不相同时相邻点的权重也不相同。若存在 3 个度为 7 的点相邻,由前面染色知,φ(vn)[11,14],φ(vs)[15,20]。根据染色方案(EC),总能找到 3 个不同权重来区分度为 7 的相邻点。对于度为 9 的相邻顶点,因为φ(vt)[21,24],所以总能在C1～C4中找到一种令这 4 个相邻的9度点的权重不同的边染色。

图6 树D2的构造示意图