两相混合式步进电机矢量控制

马丹晨

（知行机器人科技(苏州)有限公司，江苏苏州，215400）

0 引言

步进电机具有机械结构简单、没有累计误差、控制灵活、成本较低等优点被广泛的使用在自动控制领域，比如打印机、机床、机器人等，但是步进电机有着很明显的缺点，低速运动由于步距角太大使电流不连续会产生振动，高速电机会产生失步的现象，所以很多高精度的场合并不适用步进电机。因此为了适应工业界的发展人们将永磁同步电机矢量控制方法的思想引入到了步进电机中来，由于电机结构的不同，人们对步进电机的矢量控制在不同的方向上进行了简化，文献[1]采用了恒流斩波的驱动方式实现了步进电机步距角的128细分，文献[2]采用了将量化的步进电机细分电流制成了表格，存入软件的数组中，使用时根据数组中的数据给定期望的电流，再通过采集相电流形成闭环的系统，可以实现256细分的驱动控制。这些控制方式都是可以增加步进电机的细分数和运行的平稳度，但是还是对矢量控制的过程做了一定程度的简化，不能实现任意细分。因此本文将从矢量控制根本性原理进行详细推导，从而实现任意细分和恒力矩的步进电机驱动器。

1 系统设计

1.1 两相步进电机系统模型

两相步进电机的矢量控制系统框图如图1所示，和三相永磁同步电机的SVPWΜ类似，两相步进电机的矢量控制是由坐标变换部分的反向park变换开始的，经过反向变换后直流信号变成了交流信号，再经过SVPWΜ模块处理最后输出的是正弦波（这里因为两相步进电机的特性其最后输出的是正弦波），在通过系统的电压测量模块，采集Iα和Iβ两项的电流，经过park变换后后输出给PID控制器，以此形成一个闭环。

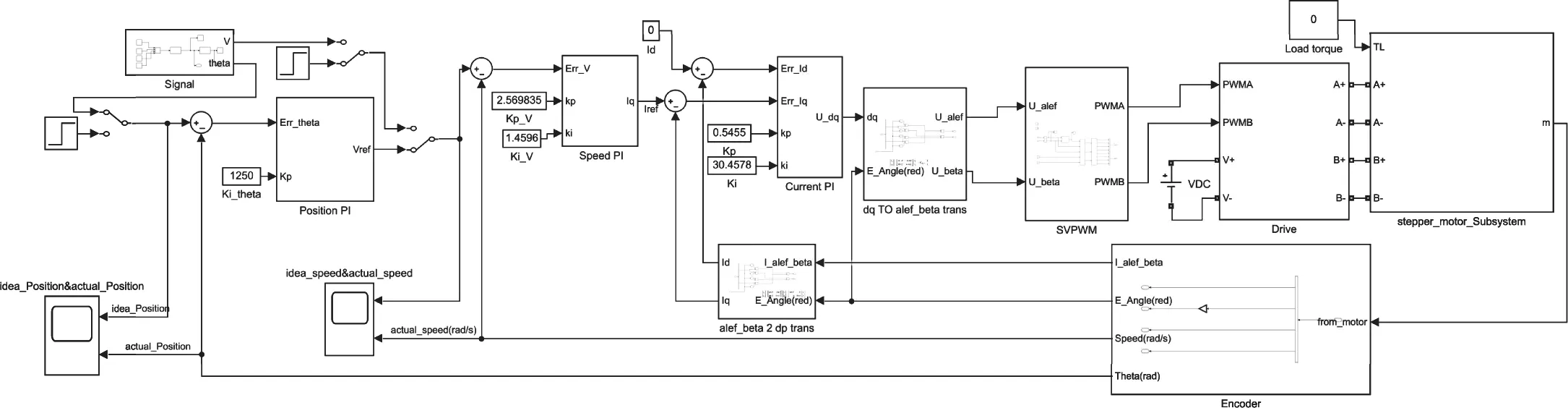
图1 两相步进电机矢量控制框图

步进电机的转矩特性如式(1)所示。

其中L1为定子绕组的自感基波分量，在此数学模型中我们假设A相定子和B相定子的基波分量相等；theta为转子的电角度，Nr为转子的齿数Μsr为定子和转子之间的互感系数，Im为转子的励磁电流。

步进电机的电压方程如式(2)所示。

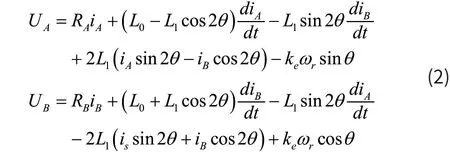
式中RA和RB两项表示绕组A和B的内阻，Ke为反电动势，Wr表示转子速度。电机的转矩机械运动方程如式(3)所示。

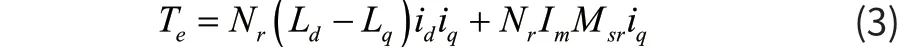
1.2 两相步进电机坐标变换

两相步进电机在进行坐标变换的时候不需要进行crack变化和反crack变化，所以我们只列出了Park变换和反向Park变换，变换过程如图2所示，转子的磁链轴为d轴。经过坐标变换，iα、iβ坐标系中的直流电信号被转换为dq坐标系中的交流电信号，它们的变换过程如式(4)、式(5)所示。

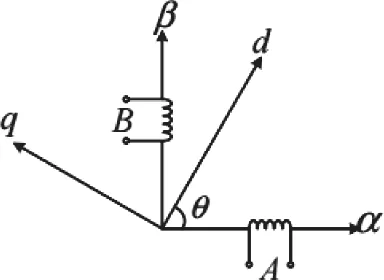
图2 两相步进电机坐标变换示意图

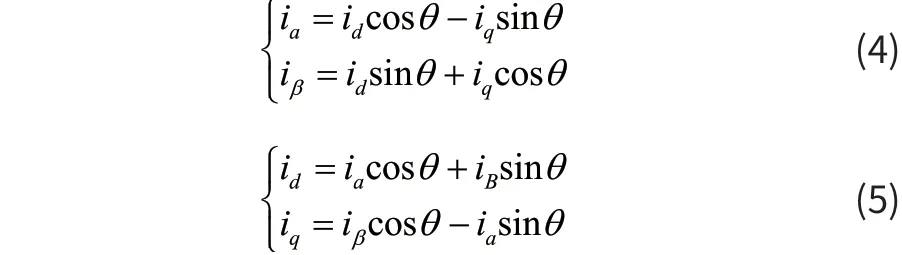
1.3 两相步进电机SVPWM模块

经过反向Park变换后得到两个交流电压Vα和Vβ，将之送入SVPWΜ模块，由SVPWΜ模块输出三相交流电压。SVPWΜ实际上要处理的过程分为三步，第一步进行扇区判断，判断矢量合成在哪个扇区，第二步通过两个相邻的矢量计算预期的矢量作用时长，第三步将第二步算出的适量作用市场转换成计数器的比较值。

两相步进电机驱动电路H桥拓扑图如图3所示，可根据开关管的不同状态组合成16个空间状态图4为空间矢量分布情况，该图反应了这16个状态所处的位置。有12个非零状态和4个零状态。我们选用其中的4个非零矢量将空间分成4个扇区，表1列出了这4种矢量分布的状态。简化后分割情况如图5所示。U0表示V0（0000），U1表示V8（1000），U2表示V2（0010），U3表示V4（0100），U4表示V1（0001）。

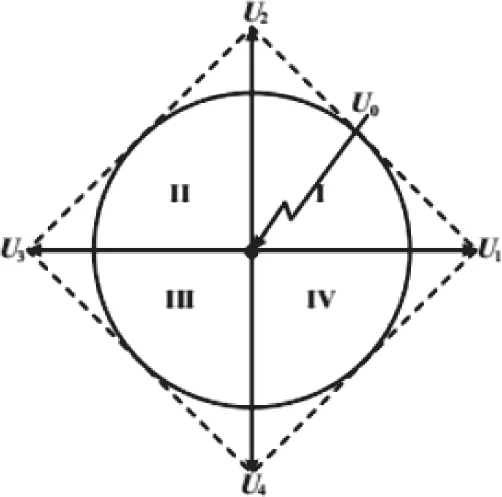
图5 矢量分布情况

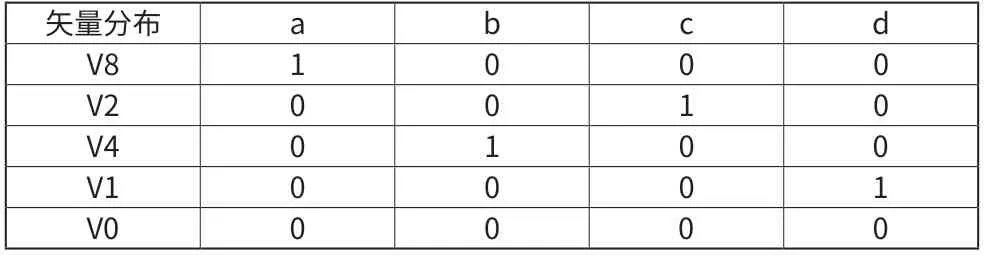
表1 矢量状态表

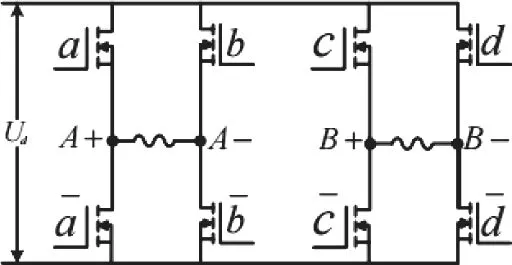
图3 H桥电路拓扑

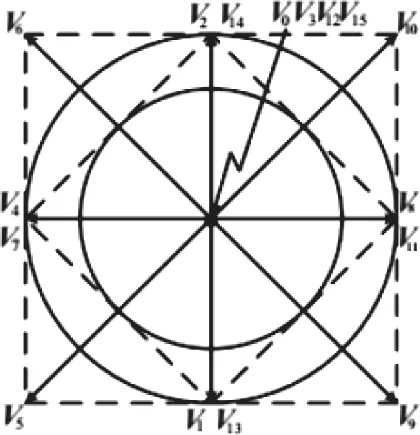
图4 矢量状态分布图

经过坐标变换，得到了合成矢量Uref在静止两相正交坐标下的分量Uα和Uβ，合成矢量的坐标分量如图6，接下来就是判断扇区的过程，若合成矢量Uref在矢量分布图的第一象限，则有Uα>0，Uβ> 0；若合成矢量Uref落在了第二象限，则有Uα<0，Uβ> 0；若合成矢量落在了第三象限，则有Uα<0，Uβ< 0；若合成矢量落在了第三象限，则有Uα>0，Uβ< 0，可见合成矢量Uref所在的位置可以通过Uα和Uβ推导而出。

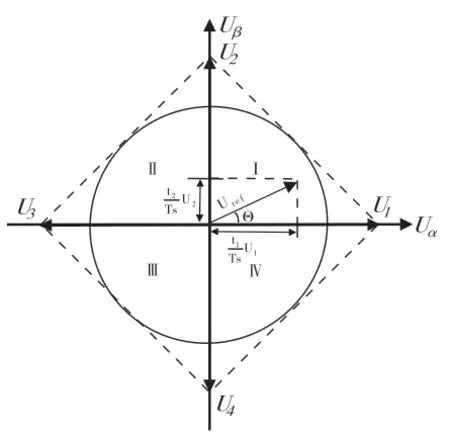
图6 合成矢量

为了方便于软件的编程我们需要更加直观的方法来告诉处理器我们合成矢量所在的扇区，因此我们做出假设，将Uα和Uβ的状态分布用二进制来表示，并且用A表示Uα的状态，用B表示Uβ的状态，如式6。由于A、B组合起来可以表示四种状态，我们在定义一个变量N，使得N=1+A+2B,即可在程序中用N来表示合成矢量Uref到底落在了哪个象限。合成矢量Uref所处的象限与N的关系如表2所示。

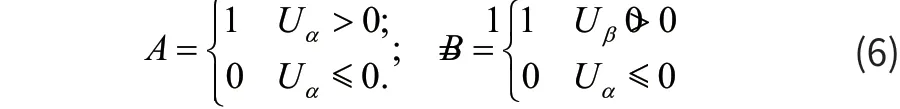
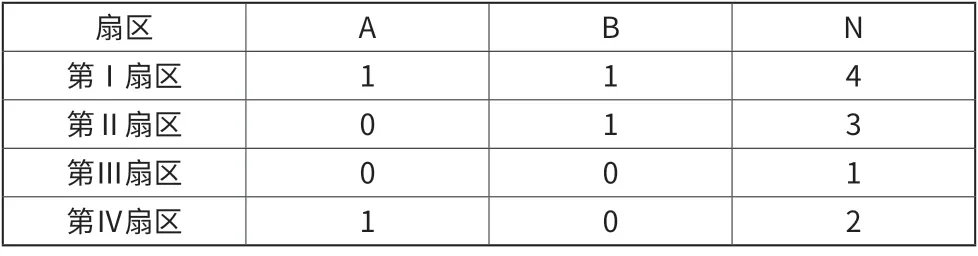
表2 扇区与N的关系

判断完合成矢量后我们需要进行第二步用相邻的两个矢量去合成我们预取的矢量在正交坐标系下的分量时长，参考图6，在第一扇区，我们可以根据角度信息和矢量的大小来将合成适量Uref分解为Uα和Uβ，在软件实现上，我们可以设定一个PWΜ的周期性波形，周期为Ts，Uref被分解等效于在正交坐标轴上U1和U2两个方向的时间分量t1，t2和零矢量的作用时长t0。这里直接得出结论，详细的推导过程见文献[4]。当合成矢量U ref 处在第一扇区时，时间分量t1=Ts/Ud ＊ Uα,t2=Ts/Ud＊ Uβ；当合成矢量U ref 处在第二扇区时，时间分量t1=Ts/Ud ＊ Uβ,t2=-Ts/Ud＊ Uα；当合成矢量U ref 处在第三扇区时时间分量t1=-Ts/Ud ＊ Uα,t2=-Ts/Ud＊ Uβ；当合成矢量U ref 处在第三扇区时时间分量t1=-Ts/Ud ＊ Uβ,t2=Ts/Ud＊ Uα。由此我们令Tx=Ts/Td ＊ Uα,Ty=Ts/Td ＊ Uβ,可以得到合成矢量Uref在各个扇区和其相邻矢量的关系如表3所示。本文所采用的svpwm为五段式，其每一个的扇区的电压波形图如图7所示，我们再根据该波形图算出定时器4个通道比较值，当定时器计数值到达该位时我们控制电平的变换。到这里完整的矢量控制算法的推导过程算是结束了。

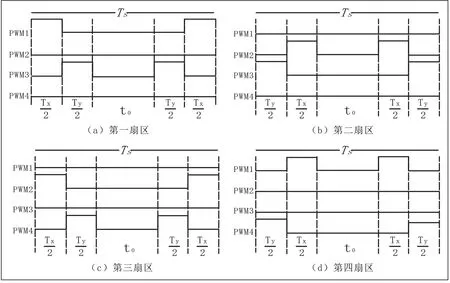
图7 五段式SVPWM

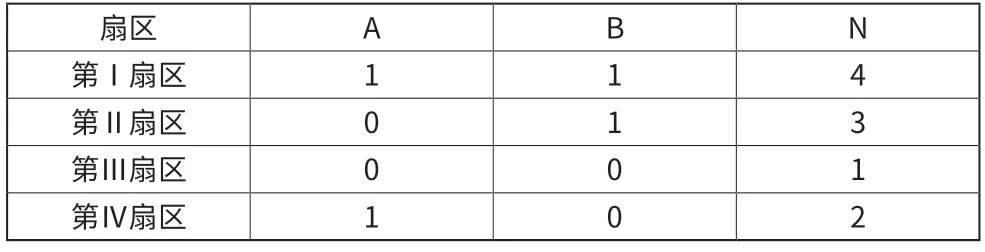
表3 合成矢量与相邻矢量的时间关系

2 硬件方案

介绍了SVPWΜ的算法，算法需要在硬件上实现，为了避免一些读者为了找硬件方案去实现算法，这里我们会介绍编码器的选型、电机驱动芯片的选型和ΜCU的选型。

2.1 编码器选择

电机闭环控制离不开编码器，在开发两相步进电机的方案上，编码器一般使用磁编码芯片譬如AS5145、AS5147、ΜQ732、ΜT6816、ΜT6825等等，可以根据方案需求选用合适的编码器芯片，当然光电编码器也可以用在电机开发控制上，可以选用分辨率1000线的，在软件采集信号的时候可以四倍频达到比较高的4000分辨率，光编码器位置测量比较稳定，但是易损，而且比较容易受到污染，磁编码器精度较高、性能可靠、结构简单但用在电机控制中一般为一个磁编芯片，没有计圈功能，如果没有齿轮箱的协助只能通过电子计圈来实现位置计数，但是这样就增加了累计误差。

2.2 驱动芯片选择

目前电机驱动芯片流行的有A4950、A4955、DRV83 01、TB67H450等等，这些电机驱动芯片驱动能力在3A左右，像A4955、TB67H450甚至可以实现硬件FOC矢量控制，我们只需要实现PID控制。当然其实现方式还是较为复杂，一般都将量化后的电流值组织成一张表，输出电流时根据表中的数据输出相应的电流值，当然这么做细分数肯定会受到一定程度上的限制。 当然为了我们电路板的驱动能力更强，我们一般使用内部没有集成ΜOS管的驱动芯片比如A4955，DRV9301。

2.3 MCU芯片选择

电机控制的ΜCU尤为重要，因为在进行矢量控制的时候需要大量的运算，而且需要产生很高精度的PWΜ波形，如果PWΜ波形不够精密，那么就无法做到恒扭矩，因此这里我们推荐市面上最常用的STΜ32系列的芯片，最好选择Μ4内核的芯片，因为Μ4内核的芯片大部分都带有硬件浮点运算FPU，可以加快除法的运算，STΜ32系列的库比较丰富，在开发速率和仿真调试方面有着比较大的优势。

2.4 系统设计

根据系统架构，搭配合适的步进电机选型，该方案已经可以在标准的28、42和57电机的驱动控制灵活使用。配合优化PID参数的调整和控制环路的设计，电机在中、低、高转速下均可以实现精确的力矩、速度和位置控制。可以在程序中开发相关的通信协议，调试接口API和对应的上位机调试工具，梯形加减速和S型加减速，并且支持分段的运动控制。可以为电机在各自动化和机器人的场景中应用做灵活开发。

3 总结

细分驱动器将步进电机的步距角更加细化的分成了很多步，步进电机因此可以大幅的提升运动精度和减小步进电机的低频振动和噪声，本文首先建立了两相步进电机的矢量控制流程和建立数学模型，利用矢量控制的思想设计两步进电机的细分控制器，总的来说分为四个步骤，第一步进行坐标变换，将直流信号转换为交流信号，第二步进行扇区判断，判断合成的矢量Uref处在哪个扇区，第三步计算分解矢量在对应坐标轴上的作用时长，第四步采用软件方法将作用时长转换为计数器的比较值生成五段式的SVPWΜ。最终实现了恒扭矩，可以任意细分的步进电机驱动器。增加了步进电机的运动的稳定性和平滑性，提高了步进电机的运行精度，步进电机电压利用率达到了理论上的100%，使步进电机可以应用在更多精密的场合。本文提出的SVPWΜ算法是两相步进电机的SVPWΜ，相信研究过无刷电机矢量控制的读者一定可以发现每一步推导过程都是与无刷矢量控制一一对应的。