二阶再生张量空间与再生张量的性质
2022-03-13殷洪才全玉锦
殷洪才,全玉锦
(1.广东外语外贸大学;2.辽东学院)
0 引言
张量是数学的一个重要分支,近代物理和力学的发展促进了它的充实与完善.它的应用也越来越广泛.在文献[1]中作者在光学领域应用张量研究了反射线;在文献[2]中作者在材料力学中应用张量研究了弹性问题;在文献[3]中作者在Dirac场的重正化提出了张量和Casimir效应;还有核物理等方面的应用[4].
该文将张量以线性空间来描述,进而建立泛函分析相应结构,尤其是将再生核概念引入到张量中去.再生核本是泛函分析中一种正定的积分核[5],从某种意义上看,它是Riesz表现定理的实现[6].近年来,再生核在物理模型计算中有着积极的贡献[7-15].该文就是在将这些积极的因素引入到张量分析中,扩大再生核计算优势,相信这将对物理领域中的研究、尤其是在计算物理中开辟一种新的计算方法来.
1 一些预备知识与符号
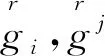
(2)协(逆)变基矢量新老转化关系

(4)两个张量(阶数≥2)的双点内积
设张量

2 二阶张量空间
基于张量的一些已有运算从公理化角度严格叙述,使得二阶张量构成一个赋范空间.为再生引入奠定基础.

定理2.1 假设gij是正定矩阵,则Ω在张量加法、数乘和双点内积下构成内积空间、赋范空间.
证明仅检验内积公理.也仅对张量协变型式检验,
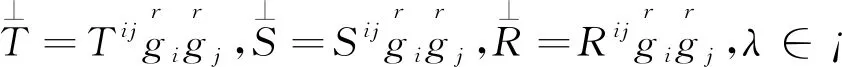
(1)内积正定性
和
(2)交换性
(3)数因子结合性
(4)分配率
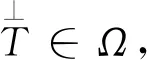
3 二阶再生张量空间与再生张量的性质
再生性质本是Riesz表现定理[6]对线性泛函理论表示提出来的,即对任意空间H上的连续泛函f(x),必存在H唯一的元y,使得f(x)=

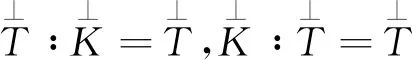
(1)

定理3.1 二阶张量空间Ω是再生张量空间.
证明取四阶张量:


(2)

定理3.2 张量空间Ω是再生张量空间的再生张量(2)是唯一的.
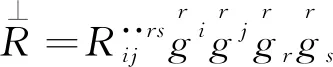

而
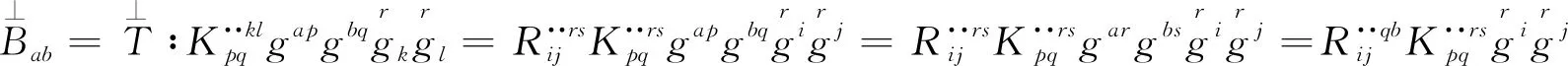


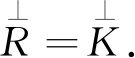

(3)
是Ω的一组基.
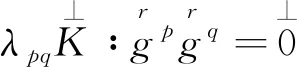


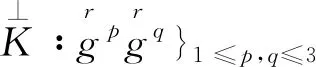
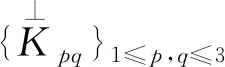
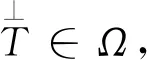
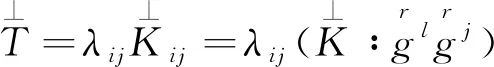
4 结束语

