基于特征融合和尺度自适应的核相关滤波算法研究

赵 亮，谭功全，周 晴，杨 锴

（1.四川轻化工大学自动化与信息工程学院，四川 宜宾 644000；2.人工智能四川省重点实验室，四川 宜宾 644000）

引 言

目标跟踪在计算机视觉领域中具有重大研究价值［1］，实时的目标跟踪在行人检测、自动驾驶、视频监控等领域得到广泛的应用［2-3］。但在现实场景中，目标由于遮挡、光照变化、运动模糊等因素导致跟踪效果不好，目标丢失等问题［4］也经常发生。因此，提高跟踪成功率与准确度成为跟踪领域中的研究重点［5］。

相关滤波算法由于其速度快，精度较高，成为目前运用广泛的跟踪算法［6］。Bolme 等［7］提出的MOSSE（Minimum Output Sum of Square Error）算法是最初应用到核相关滤波的算法，跟踪速度达到669 fps，但由于只能利用第一帧中的有限信息进行学习，导致训练样本很少，因此很容易产生漂移现象［8］，并且会让跟踪器不可恢复。因为其速度快，可移植性强，进而CSK（Circulant Structure of Tracking with Kernels）算法在MOSSE 算法的基础上加入正则项，防止滤波器过拟合［9］。之后Henriques 等［10］提出的KCF（Kernelized Correlation Filter）算法使用HOG特征，并且引入循环矩阵和核函数，使得相关滤波算法在保持高帧率的情况下跟踪精度也有了极大提升。但由于算法使用单一的特征，而且缺少尺度更新机制，导致跟踪鲁棒性差。与此同时，Danelljan 等［11］也提出了使用颜色特征的CN（Color Name）算法。

2014 年，Li［12］提出将HOG 特征与CN 特征串联融合的SAMF（Scale Adaptive and Multiple Feature）算法，在进行目标定位的同时求解最佳目标尺寸。该算法的多尺度方法是使用尺度池的方式，将平移滤波器在多尺度缩放的图像块上进行目标检测，然后计算检测的响应值，并取得响应最大的平移位置及所在尺度，最后，在7 个尺寸上得到7 层响应，取最 大 响 应 作 为 最 佳 尺 寸。Daneljan 等［13］提 出 的DSST（Discriminative Scale Space Tracker）算法同样也加入了尺度变化，通过引入一维滤波器完成目标的尺度估计。此算法仅使用了HOG 特征，在使用位置滤波器检测响应值最大的位置的同时，又训练了检测最佳尺度的尺度滤波器。该尺度滤波器取33个尺度，并计算这些尺度和原图片的响应值，在响应最大处取得最佳尺度。近几年基于深度学习的跟踪方法也层出不穷，例如基于孪生网络的SiamFC算法［14］、采用RPN 网络对目标尺度回归的SiamRPN算法［15］以及增加分割功能的SiamMask算法［16］。

在核相关滤波的框架基础上，本文研究了不同特征的变化规律，以及被跟踪目标所发生的尺度变化，提出一种自适应目标尺度更新方式。并且在特征提取上进行HOG 特征与CN 特征自适应融合，从而改进跟踪算法。

1 KCF目标跟踪算法原理

线性岭回归的目标函数可表示为：

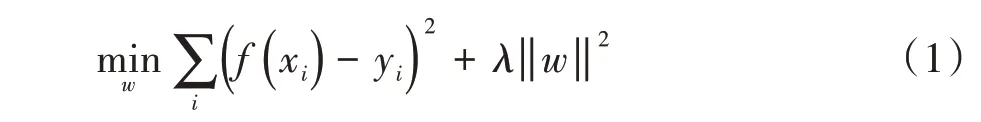
式中：函数f为分类函数，xi为样本，yi为样本标签，λ为正则化参数，防止过拟合现象，w为滤波器系数。岭回归具有闭解式如下：

式中：I为单位矩阵，X为循环矩阵，y为样本标签矩阵，式（2）在复数域中为：

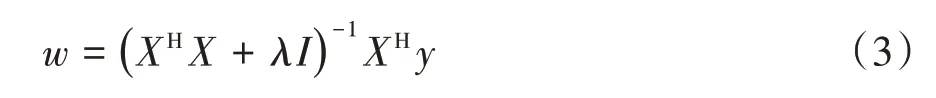
式中：XH为X的共轭转置。

假设有一个一维数组x=[x1,x2,…,xn],通过构造循环矩阵对x进行循环移位，使负样本的数量增加，循环移位算子P为置换矩阵：

其中：u为向量x的元素向右平移的单位数。当进行了n次移位后就得到最终样本矩阵X，由式(5)得到的集合可计算出最终样本：

所有的循环矩阵在傅氏空间中可使用离散傅里叶矩阵进行对角化得到：

式中：α为w的对偶空间变量，k为核函数，z为检测样本集。对核函数使用循环技巧，可得到岭回归方程的解为：

该算法只需要进行简单的点乘、傅里叶与反傅里叶变换，因此运算速度大大提高。通过以上步骤可获得滤波器模板，在下一帧的此区域附近通过循环移位得到的样本集z，滤波器与z相关响应的傅里叶变换可得到：

跟踪过程中由于目标外观发生变化，长时间的跟踪会使效果变差，进而引入了模板更新机制，主要是采用线性内插法更新分类器的α^ 与目标特征向量x^：

笔者认为，医院建筑设计中最核心的问题是如何最大限度满足使用者的需求，并处理好该建筑与自然之间的关系。指导建筑设计，著名建筑师章斌欢女士曾指出：新世纪的建筑，无论是整体规划还是单体建筑的外部设计或内部功能，无论是从物质上还是从精神上“以人为中心”-“以人为本”的设计思想已是无可争论的。因此，建筑设计师不应只是以建筑物的功能为设计的出发点，而应该在设计的过程中充分考虑使用者的需求、使用者的主观感受以及建筑本身与自然之间的和谐关系等等。

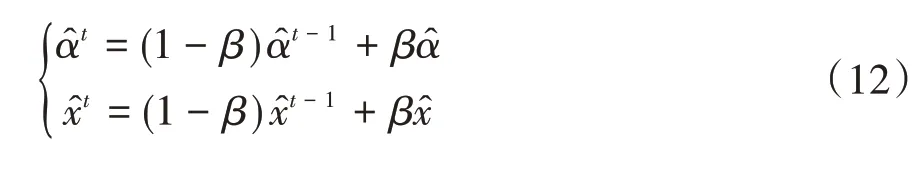
式中：t为视频的帧数，β为线性内插因子，能长时间跟踪目标。但由于KCF 算法中只有单一的HOG 特征，导致跟踪中存在鲁棒性差、尺度不更新等问题。

2 本文算法

2.1 特征融合

目标跟踪的重要一步为特征提取，一种合适的特征提取方式可以很大程度地提高跟踪效果。传统的算法大多应用的是单一特征［17］。但是任何单一的特征都有其侧重点，如HOG 特征是在图像的局部方格单元上操作，所以它对图像几何的和光学的形变都能保持很好的不变性。但是由于梯度的性质，使其对噪点比较敏感。而颜色特征作为一种全局特征，可以很好地描述图像区域内对应景物的表面性质，且不受目标大小和形状的影响，使其具有旋转不变性［18］，但是强烈的光照变化会使目标丢失。因此，两种特征可以达到很高程度的融合［19］，将二者结合起来，会使其达到特征的优缺点互补的目的。

近几年优秀的目标跟踪算法大多采用特征融合的方式［20］。在理论上，融合的特征越多，跟踪效果越好，但是相应的，速度会越来越慢，而且融合的特征越多，会更大几率导致提取的特征冗余。因此，大多数算法融合的特征不超过3 种［21］。本文尝试采用梯度和颜色特征相融合，重点解决目标运动模糊和光照变化产生的影响。

首先，通过前一帧提取的目标特征和所训练的滤波器进行匹配，根据匹配得到的响应分数，得到的最大响应分数即为目标位置。并且得到的最大响应分数，取决于当前帧的CN 特征和HOG 特征所占用的特征比重。因此，为了得到两种特征最优的比重，对候选样本进行建模，得到特征模型RCNt和RHOGt，采用式（13）可以得到第t帧HOG 特征和CN 特征值之比μ为：

式中：RCNt与RHOGt分别为第t帧CN特征值和HOG特征值。将式（13）中得到的权重进行特征模型融合，可求得：

由式（14）计算得到的特征模型与滤波器进行匹配，然后算出最大响应值，进而确定目标位置。

特征自适应融合的方法，在光照变化等条件下，对HOG 特征的使用效果更好，则提高HOG 特征的权重。相反，在目标发生运动模糊的情况下，则使用CN 特征的效果更好。因此，使用两者自适应融合能提高对目标的特征判别能力。

2.2 尺度自适应

首先，通过特征点检测的方式得到特征点的位置和尺度，并在当前帧的目标处采用BRISK 特征采样。匹配当前帧和下一帧的两个BRISK 特征，采用汉明距离计算它们之间的匹配度，若小于阈值，代表匹配不成功。反之，若两帧之间的匹配度大于阈值，则使用RANSAC 方法去除匹配点并计算仿射变换矩阵Pi且与下一帧目标进行比较，判断尺度变化。设当前帧特征点位置为[xi yi]T，下一帧特征点位置为[xi+1yi+1]T，则可得到：

其中：bx和by分别表示目标在横、纵坐标上的移位，cx和cy分别表示目标在横、纵坐标上的缩放值。

图1 所示为dog 视频两帧之间BRISK 特征的尺度对比图。图1中采集到小狗的特征进行两帧之间的匹配，匹配效果明显，可以由匹配结果看出目标在变小。

图1 dog视频两帧之间BRISK特征尺度对比

3 实验与分析

为了验证本文算法效果，本文在OTB2013 数据集上的不同属性集下，和另外两种对于KCF 算法改进的SAMF算法和DSST算法进行了实验对比。

3.1 实验验证

实验仿真软件为Windows10 系统下的MATLAB2018b，实验用到的计算机配置为AMD Ryzen 5 4600H with Radeon Graphics 3GHz 的处理器，运行内存为16 GB。

针对传统KCF 算法存在的光照变化(Illumination Variation)、运动模糊(Motion Blur)、发生遮挡(Occlusion)等情况，加入颜色特征与尺度变化进行改进，得到部分算法对比的精度与成功率。

图2 所示为光照变化情况下的测试结果。图2中可见，在光照变化的条件下，仅加入HOG 特征的DSST 算法，要比同时加入两种特征的SAMF 算法效果好。KCF_ours 由于采用自适应特征融合的方式，在光照变化下，CN 特征所占的权重会减小，HOG 特征增大，因此在准确率和成功率上分别比SAMF 算法提高了2.8%和0.6%。相较于KCF 算法在精度和成功率上分别提升3.1%和17.2%。

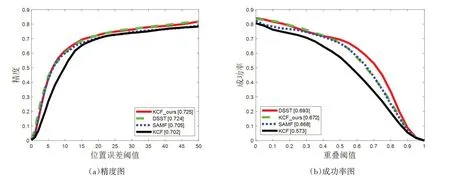
图2 光照变化属性视频序列下准确率和成功率

图3所示为在目标运动模糊的情况下的测试结果。图3中可见，双特征融合的SAMF与KCF_ous算法的优势就凸显出来。但KCF_ours 算法应用的BRISK的尺度自适应特征，要比SAMF算法的7个尺度池特征在运行速度上更快，当目标快速运动导致模糊情况下的效果更好。在准确率与成功率上分别比KCF 算法提高了10.4%和10.8%。而DSST 算法采用33个精细的尺度特征，反而比KCF算法在准确率与成功率上分别下降了9.5%和7.9%。

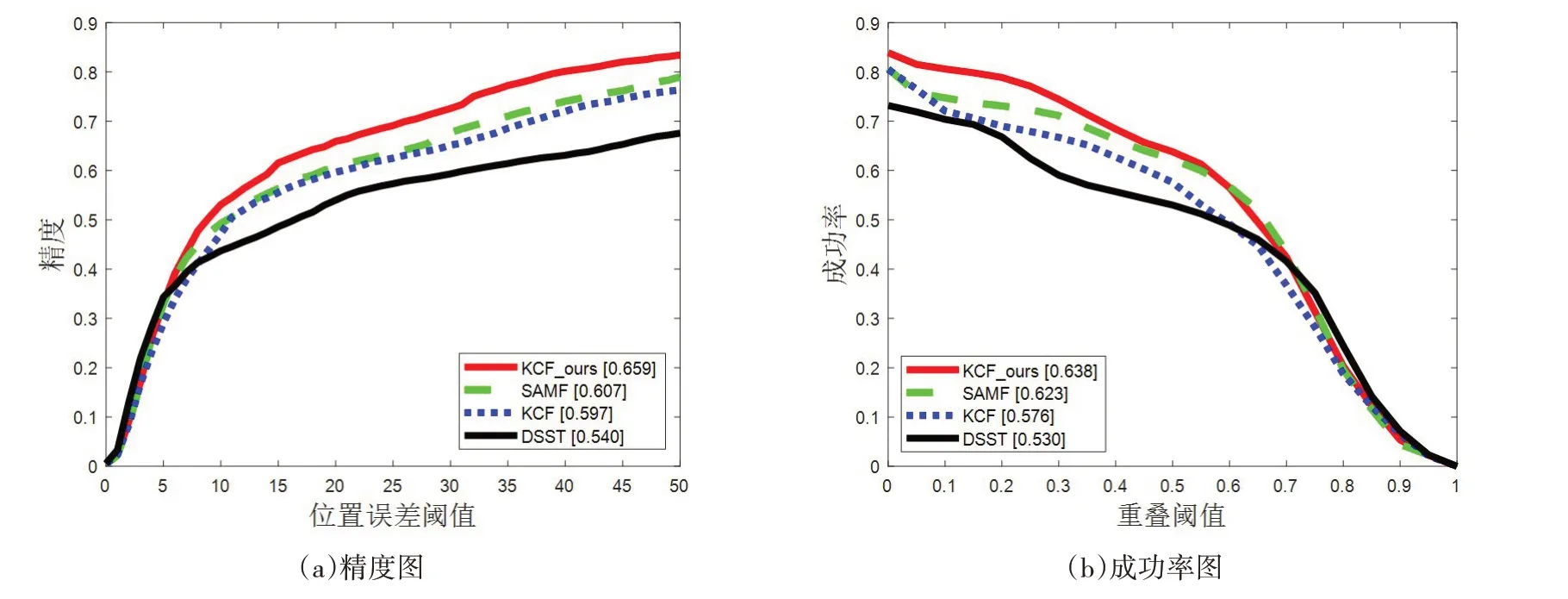
图3 运动模糊属性视频序列下的准确率和成功率

图4所示为在遮挡属性视频序列下的准确率图和成功率图。在目标发生遮挡情况下使用BRISK的尺度自适应特征要比SAMF 算法的尺度池方法效果更好，即便在半遮挡的情况下也会识别到目标位置。其准确率和成功率分别比KCF 算法提高20.8%和32.5%。

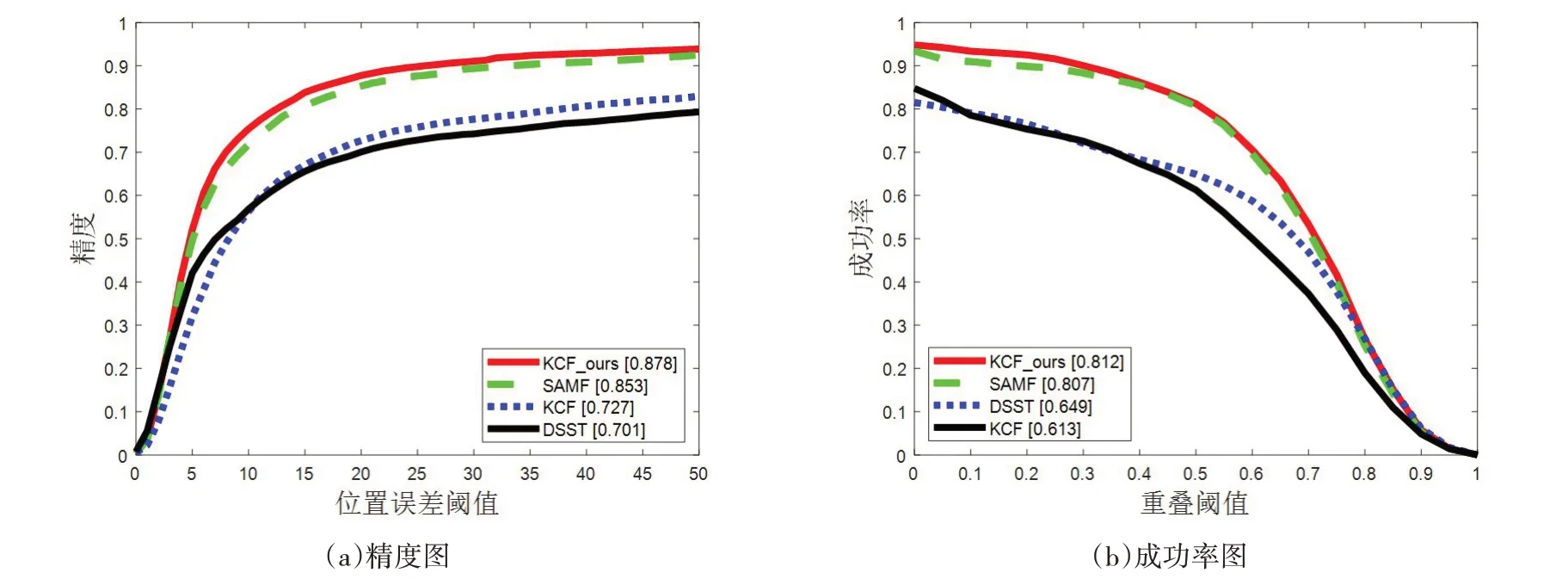
图4 遮挡属性视频序列下准确率和成功率

图5所示为所有视频序列下的测试结果。本文算法在准确率上比SAMF 算法略有提高，在成功率上稍有下降。但跟踪速度几乎为SAMF 算法的两倍，且相比于KCF 算法在准确率和成功率上分别提升了9.3%和17.7%。

根据实验中每种算法处理数据集的平均速度，得到4种算法的平均跟踪速度，见表1。KCF算法只采用了HOG特征，平均速度达到246.23 fps，DSST算法在此基础上增添了尺度特征，速度达到51.32 fps。SAMF 算法既增添了尺度特征，又加入了特征融合，效果很好但是速度偏慢。KCF_ours 算法采用自适应特征融合和BRISK 尺度特征，因此跟踪效果更好，跟踪速度相对SAMF 算法也更快，达到45.88 fps。

表1 4种算法的跟踪速度

3.2 定性分析

图6 所示为算法跟踪示例，其中红色、绿色、黄色和蓝色的跟踪框分别代表KCF 算法、SAMF 算法、DSST 算法和本文提出的算法。由图6 可见，第一行图片为OTB2013 数据集的CarScale 图像序列，图像序列中主要涉及了尺度变化，KCF 算法由于没有尺度特征，以至于在小车尺度变大时跟踪框还维持初始大小。SAMF算法的尺度特征为7个尺度池，如果参数设置得紧密，在目标发生快速的尺度变化时，跟踪框无法及时扩大。DSST 算法应用33 个尺度来判断每帧的变化，所以只有本文算法与DSST 算法跟踪效果较好。第二行为Soccer 图像序列，其中主要涉及遮挡和轻微的运动模糊，在第277帧，KCF 算法由于目标运动模糊导致跟踪丢失。同样DSST 算法和SAMF 算法在目标发生遮挡的情况下跟踪丢失，但SAMF 算法由于目标特征变化太快，尺度池的尺度变化更明显，导致跟踪框不断扩大。只有本文算法的尺度特征跟踪效果良好。第三行为Singer图片序列，其中主要涉及光照和逐渐变小的尺度变化。KCF 算法在目标尺度变小后就逐渐跟踪丢失，在177 帧，由于强烈的光照变化，SAMF 算法明显比DSST算法和本文算法的跟踪框变大，只有本文算法和没有加入颜色特征的DSST 算法效果较好。因此，本文算法在目标发生光照变化、尺度变化和目标遮挡等情况下都始终能稳定地跟踪目标。

图6 跟踪示例

4 结束语

在KCF 算法的基础上，通过研究KCF 算法的不足，进行特征融合和尺度自适应的改进方面提出一种新的算法。首先在HOG特征的基础上加入CN特征，进行特征融合，之后通过BRISK 特征匹配方式判断目标的尺度变化。实验表明，本文算法提高了目标存在光照变化、运动模糊、遮挡等情况下的成功率与精度，跟踪性能较好，并且跟踪速度达到45.88 fps，满足实时跟踪性能。