Kinetic Alfv´en waves in a deuterium-tritium fusion plasma with slowing-down distributed α-particles
2022-03-12FeiFeiLu路飞飞andSanQiuLiu刘三秋
Fei-Fei Lu(路飞飞) and San-Qiu Liu(刘三秋)
1Jiangxi Province Key Laboratory of Fusion and Information Control,Department of Physics,Nanchang University,Nanchang 330031,China
2School of Materials Science and Engineering,Nanchang University,Nanchang 330031,China
3NCU-ASIPP Magnetic Confinement Fusion Joint Laboratory,Institute of Fusion Energy and Plasma Application,Nanchang University,Nanchang 330031,China
Keywords: kinetic Alfv´en wave,dispersion relation,deuterium-tritium fusion plasma
1. Introduction
Kinetic Alfv´en waves (KAWs) are low-frequency electromagnetic waves invoked by Alfv´en waves through mode conversion, playing an extremely important role in many dynamical processes occurring in space,[1]astrophysics[2]and laboratory[3,4]plasmas. Theoretical studies of KAWs in burning plasmas are aimed at understanding heating plasmas[5-7]and driving current[8,9]in direction of ambient magnetic fieldB0. Due to the presence of local spatial charge, ions can no longer move along the magnetic lines. Electrons,however,remain attached to the magnetic field lines because of their small Larmor radius. Therefore,KAWs have a nonzero electric field parallel toB0. Furthermore,the nonzero electric field enables the Landau resonance,where charged particles can gain or lose energy by interacting with the waves. Undoubtedly, KAWs are essential for the energy transfer processes in burning plasmas. In fact, KAWs were originally proposed by Hasegawa and Chen[10]for the purpose of fusion plasma heating. Subsequently,heating of tokamak plasmas by KAWs was confirmed in the experiments of Wesienet al.[11]Understanding the generation,propagation and interaction of KAWs is critical to unraveling and predicting the physics associated with these fundamental processes.
In general, KAWs are small-scale dispersive Alfv´en waves with perpendicular wavelength comparable to the thermal ion gyroradiusρi, but with a parallel wavelength much longer than the ion inertial lengthλi. On the one hand,dispersive properties are the fundamental subject of Alfv´en waves in plasma physics. The propagation,instability,refraction and absorption of plasma waves can be studied based on the dispersion. A lot of work related to the dispersion of KAWs has been carried out in various plasma environments.[12-16]Recently,Belovaet al.[17]proposed an energy-channeling mechanism to explain the flattening of electron temperature profiles in NSTX tokamak by investigating the dispersion relation of KAWs modified by beam-ion effects. On the other hand, since the perpendicular wavelength plays an important role for KAWs, there should be a bound onk⊥. Perkinset al.[18]estimated that the perpendicular wave number of the Tokamak Fusion Test Reactor(TFTR)should vary within the certain range of 0<k⊥<1.5 cm-1. Soon thereafter, the experimental measurements of the perpendicular wave number in the TFTR plasmas were reported.[19-22]
In D-T fusion plasmas, the energy of fusion-bornαparticles is typically two orders of magnitude higher than that of the D-T fuel ions. Compared to thermal particles,theα-particles usually deviate from Maxwellian distribution, and obey a slowing-down distribution when correctly described.[23-27]In addition,α-particles are the dominant minority particles due to their low density, large kinetic energy and high pressure in the fusion reactors. Theα-particles are expected to play a key role in current driving,plasma heating,energy transfer and plasma stability. Therefore, it is particularly important to studyα-particles physics in burning plasmas. Liet al.,[28]using kinetic theory,calculated the frequencies(ωr~106s-1)and damping rate(γe~104s-1)of KAWs in the absence ofα-particles and concluded that electron Landau damping is important for KAWs.Later,Dinget al.[29]further investigated the effects ofα-particles on KAWs and found thatα-particles made the propagation of KAWs to the central region of the tokamak plasma more difficult and reduced the KAWs amplitude.
In the present paper, the dispersion and damping rate of KAWs in a D-T fusion plasma with the slowing-down distributedα-particles, the Maxwellian distributed ions (D and T)and electrons are investigated under the framework of low frequency and short vertical wavelength assumptions,and the kinetic dispersion relation for a low-βplasma is taken into account. The paper is organized as follows. The detailed calculations of the dispersion of the KAWs are presented in Section 2. In Section 3, the analytical results of the damping rate of KAWs are given. The numerical calculations and discussions based on the D-T fusion parameters are described in Section 4. Finally, the main results are summarized in Section 5.
2. Dispersion of the KAWs
Assume that all bulk-plasma populations are expressed by the Maxwellian distribution functions D and 50%T;vαdenotes the birth velocity ofα-particles corresponding to an energyEα=mαv2α/2=3.5 MeV for fusionα-particles.
Before proceeding further, we must give an effective slowing-down temperatureTeff, defined as 3kBTeff=∫mαv2fαd3v. In what follows,we will proceed to investigate the effect of theαslowing-down distribution on the physical properties of KAWs compared to that of theαMaxwellian distribution on it at the same slowing-down temperature.
For a low frequency wave mode with a long parallel wavelength in a low-βplasma, the nondiagonal components of the dielectric tensor can be neglected. Heretofore, the kinetic dispersion equation is given by[12,14]





Different from the MHD Alfv´en waves,the dispersion relation of the KAWs depends onk⊥,which means that the waves can propagate obliquely to the ambient magnetic field.
3. Dampling of the KAWs
Assuming thatω=ωr+iγwith|γ|≪ωr,we find the expression for the collisionless damping rate of the KAWs to be given by[31,32]

in the case of slowing-down distribution,and


4. Results and discussion
To further elucidate the nature of KAWs in a D-T plasma,we will describe the dispersion relations in Eqs. (28) and(29) and damping rates in Eqs. (31) and (32). We take typical TFTR tokamak parameters with[28,29]B0= 5.2T,ne=3.2×1020m-3,Te=TD=TT=10 keV. For the TFTR device,k‖~1/RwithR=2.48 m being the major radius. Thusk‖≈0.4 m-1. Additionally, the plasma quasi-neutrality goes as 2nα+nD+nT=ne. Here, we choosenD=nT, thus 2nα+2nD=ne.
Figure 1 shows the effect ofαconcentration on the KAWs. From Figs. 1(a) and 1(b), it can be found that the frequency of KAWs increases with the increase of normalizedαdensity (nα/ne), and likewise the damping rate increases.Moreover, the values of both the frequency and damping obtained with slowing-down distributedα-particles are slightly lower than those of the equivalent Maxwellian case for a certainαconcentration. However, since theαdensity in D-T plasmas is generally less than one percent of the bulk plasma density,[24]the magnitudes of the frequency and the damping rate do not change significantly with increasingαconcentration.
From Fig.2(a),it can be seen that the frequency increases with the increase of the perpendicular wave number (k⊥ρD).Meanwhile, it can be found from Fig. 2(b) that the Landau damping is enhanced with the increasingk⊥ρD. For a givenk⊥ρD,the value of frequency in the slowing-down case is significantly smaller compared to that in the Maxwellian case.However, the damping rate in the large wave number region is slightly larger than that in the Maxwellian case,which indicates that the Landau damping in the Maxwellian distribution plasma system is slightly suppressed compared to that in the case of slowing-down distribution. In addition, for a givenk⊥ρD, as the parallel wave number increases, the frequency and damping rate increase in both the distribution cases.
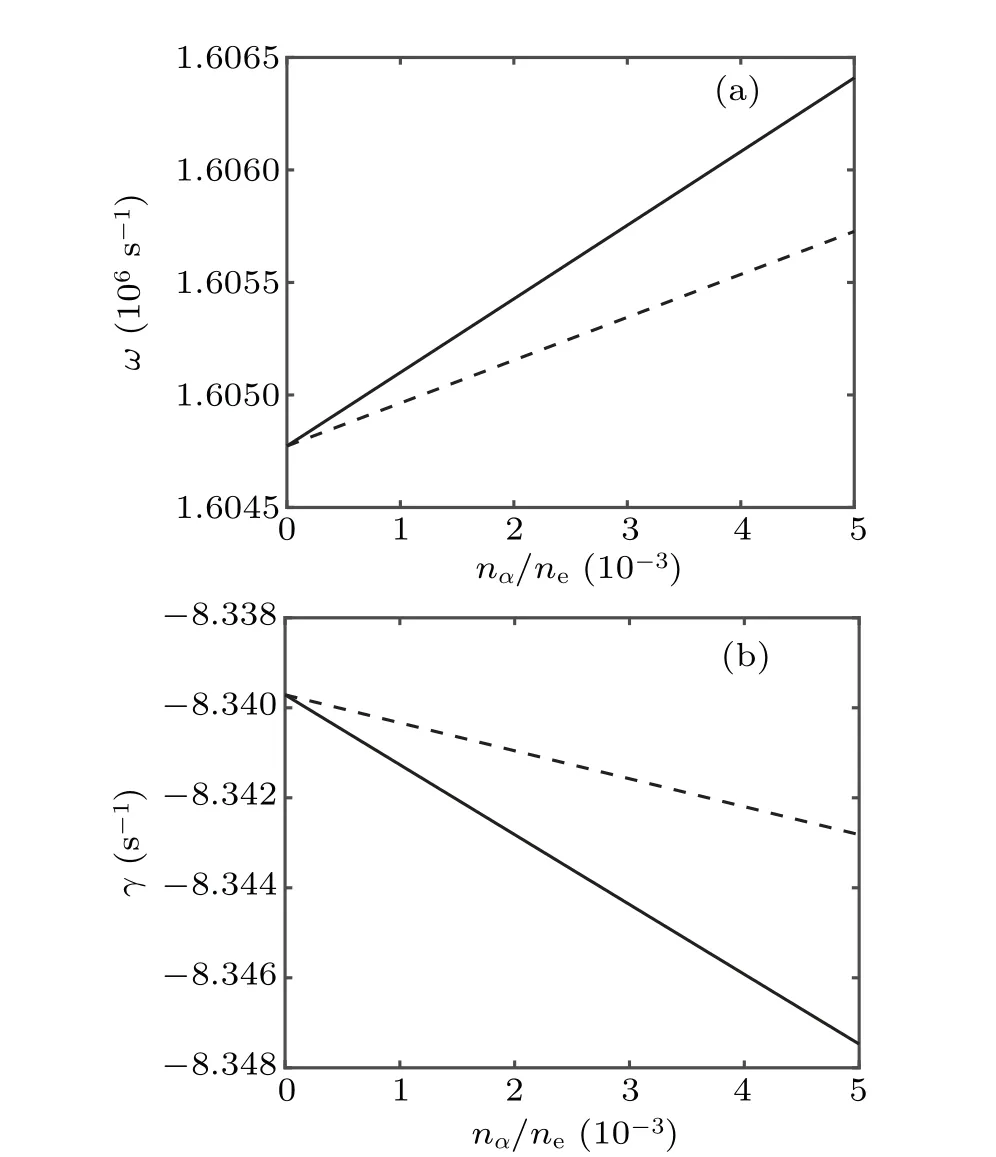
Fig.1.(a)Frequency(ω)and(b)damping rate(γ)vs normalized α density(nα/ne)for k⊥=10 m-1,k‖=0.4 m-1 and Te=TD=TT=10 keV.The solid and dashed lines denote the Maxwellian and slowing-down distributions,respectively.
As mentioned above, the perpendicular wave number(k⊥), with 0.01<k⊥<1 cm-1, is appropriate in tokamak plasma confinement experiments. Figures 3(a) and 3(b) provide the information on the variation of frequency and damping rate versus the perpendicular wave number(k⊥)under different background temperatures. From Figs. 3(a) and 3(b), it can be concluded that the higher background temperature will lead to a larger wave frequency and damping rate in both the distribution cases. Physically,when the temperature increases the finite Larmor radius of the ions increases, which leads to an increase in the real frequency. On the other hand, the dispersion of the KAWs is induced by the thermal motion of the particles,and the Landau damping is determined by the number of charge particles in the vicinity of the resonant phase velocity of plasma waves. Apparently, it can be found from Eq. (31) that the damping rate is proportional toT1/2e. The elevated background temperature intensifies the thermal motion of charged particles. Then, the number of the electrons that satisfy the resonant condition is increased, and the Landau damping is enhanced.
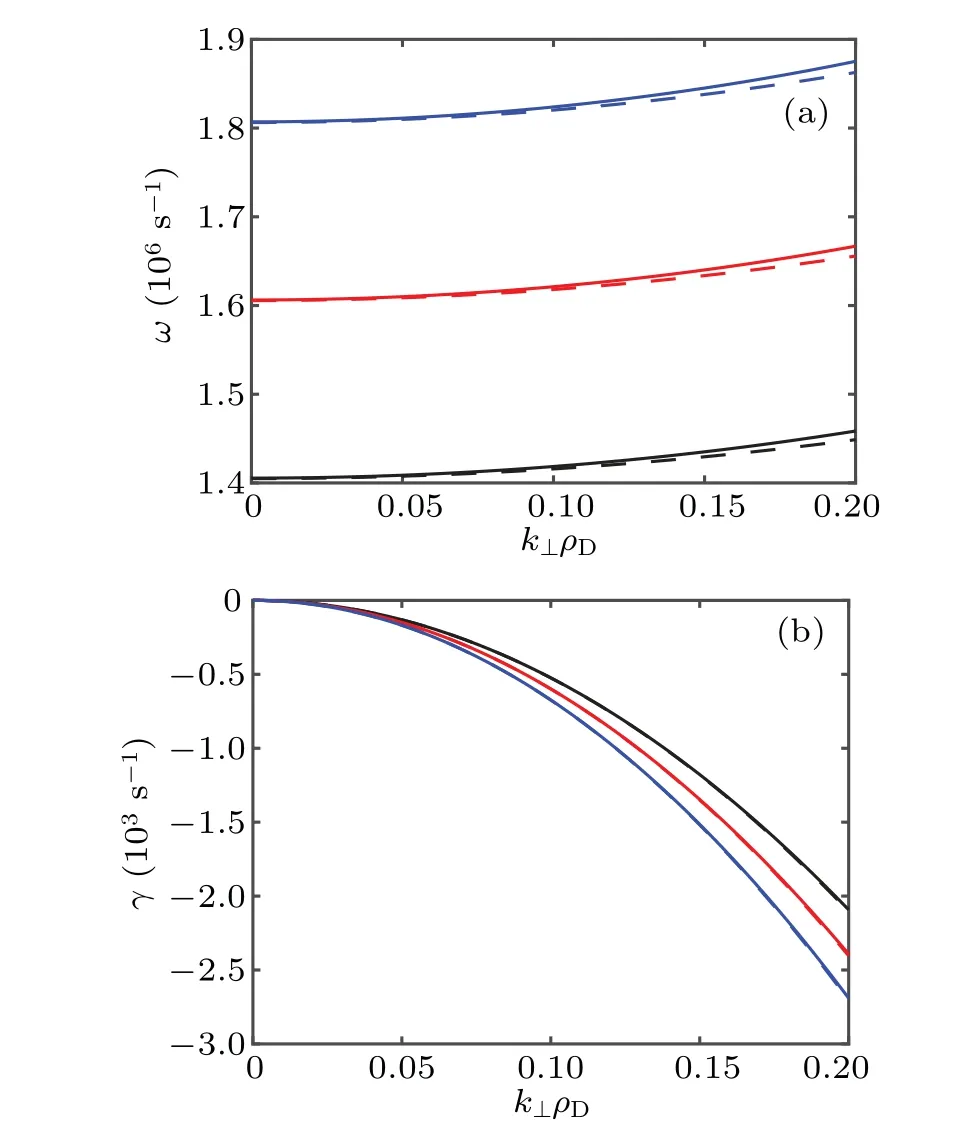
Fig.2. (a)Frequency(ω)and(b)damping rate(γ)vs normalized perpendicular wave number(k⊥ρD)for nα/ne=0.005 and Te=TD=TT=10 keV. The black, red and blue lines correspond to k‖ =0.35, 0.40 and 0.45 m-1,respectively,while the solid and dashed lines denote the Maxwellian and slowing-down distributions.

Fig. 3. (a) Frequency (ω) and (b) damping rate (γ) vs perpendicular wave number (k⊥) for k‖ = 0.4 m-1 and nα/ne = 0.005. The solid, dotted and dash-dotted lines correspond to Te =TD =TT =10,20 and 30 keV, respectively, while the red and black lines denote the Maxwellian and slowing-down distributions.
5. Conclusions
In this work, using the kinetic theory we have studied the KAWs in D-T fusion plasmas with theα-particles described by a slowing-down distribution function, as well as a Maxwellian distribution function. For low frequencyω <Ωj,short perpendicular and long parallel wavelengthk‖≪k⊥,and in the case ofk⊥ρj ≪1,the dispersion and damping rate of the KAWs are derived and numerically evaluated.
The present results indicate that both the frequency and the damping rate increase with the increase ofαconcentration. However,at the lowαconcentration,i.e.,nα/ne≤10-2,the fluctuation of theαconcentration has less effect on the frequency and damping rate of KAWs. In addition,the frequencies of KAWs obtained from both the slowing-down distribution and the equivalent Maxwellian distribution gradually increase as thek⊥increases,and the value of the frequency in the case of slowing-down distribution is smaller than that in the Maxwellian distribution. Inversely, the value of the damping rate in the slowing-down distribution is slightly larger compared to that in the Maxwellian distribution. Furthermore, it can be found that the higher the background temperatureTe,the larger the wave frequency and damping rate. The present work is conductive to the understanding of KAWs in D-T fusion plasmas,which may also be related to the nonlinear process associated with the low-frequency Alfv´en wave modes in burning plasmas,and will be investigated in our future work.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant Nos. 11863004 and 11763006), the Jiangxi Provincial Key Laboratory of Fusion and Information Control,China(Grant No.20171BCD40005),and the Project of Scientific and Technological Innovation Base of Jiangxi Province,China(Grant No.20203CCD46008).
杂志排行
Chinese Physics B的其它文章
- Surface modulation of halide perovskite films for efficient and stable solar cells
- Graphene-based heterojunction for enhanced photodetectors
- Lithium ion batteries cathode material: V2O5
- A review on 3d transition metal dilute magnetic REIn3 intermetallic compounds
- Charge transfer modification of inverted planar perovskite solar cells by NiOx/Sr:NiOx bilayer hole transport layer
- A low-cost invasive microwave ablation antenna with a directional heating pattern
