Superconductivity in CuIr2-xAlxTe4 telluride chalcogenides

Dong Yan(严冬) Lingyong Zeng(曾令勇) Yijie Zeng(曾宜杰) Yishi Lin(林一石) Junjie Yin(殷俊杰)Meng Wang(王猛) Yihua Wang(王熠华) Daoxin Yao(姚道新) and Huixia Luo(罗惠霞)

1School of Materials Science and Engineering,State Key Laboratory of Optoelectronic Materials and Technologies,Key aboratory of Polymer Composite&Functional Materials,Guangzhou Key Laboratory of Flexible Electronic Materials and Wearable Devices,Sun Yat-Sen University,Guangzhou 510275,China

2Center for Neuron Science and Technology,School of Physics,Sun Yat-Sen University,Guangzhou 510275,China

3State Key Laboratory of Surface Physics and Department of Physics,Fudan University,Shanghai 200433,China

4Shanghai Research Center for Quantum Sciences,Shanghai 201315,China

5Key Laboratory of Functional Molecular Solids,Ministry of Education,College of Chemistry and Materials Science,Anhui Normal University,Wuhu 241002,China

6College of Science,Hangzhou Dianzi University,Hangzhou 310018,China

Keywords: layered telluride chalcogenide,superconductivity,charge-density-wave,CuIr2-xAlxTe4

1. Introduction

The continuous suppression of metal-insulator(MI)transition, charge-density-wave (CDW) transition, magnetism,etc. leading to the occurrence of superconductivity (SC) in the proximity of such quantum states has garnered great interest and widespread study in solid-state physics.[1-4]The phase diagrams of unconventional high-temperature (high-Tc)cuprates and iron-based superconductors exemplified such phenomena.[5-11]Nevertheless, how SC emerges in these high-Tcsuperconductors is intricate and remains extremely puzzling. It is still essential to sort out the interplay between the SC and the other quantum states,promoting further understanding of the mechanism of high-Tcsuperconductors.

Low-dimensional layered transition metal dichalcogenides(TMDs)are other opportune material platforms for the exploration of various quantum instabilities,[12-21]especially the interplay between SC and CDW,in which the CDW order refers to condensate with periodic modulations of the crystalline lattice and conduction electron density in real space.Typically,the SC can be induced and a dome-shape superconducting phase diagram is formed upon suppressing the CDW order,[22-27]which is highly similar to the phase diagrams of unconventional high-Tccuprates and iron-based superconductors. Despite overall phase diagram similarities, there are significant differences especially between their mechanisms,

where unconventional high-TcFe-based and cuprate superconductors cannot be well explained by Bardeen-Cooper-Schrieffer(BCS)theory but most of the TMD superconductors can be explained by BCS theory. It has been generally considered that the collapse of CDW state accompanied by the improvement of superconducting transition temperature(Tc)is in reference to the abrupt enhancement of density of states(DOS)around the Fermi levelN(EF) in the conventional superconductors owning to CDW state gaps out some regions of the Fermi surface.[1,2]The formation of CuxTiSe2(0 ≤x≤0.1)from intercalating the Cu into 1T-TiSe2exemplified a vivid phase diagram in the TMDs family,[2]and further evoked the continuous interest in searching for new superconductors in TMD materials by gating, adding physical pressures, chemical doping or point contact method.[22-38]For example, Cuintercalation 2H-TaS2forms CuxTaS2(0 ≤x≤0.12)and displays an enhancement ofTcfrom 0.8 K (x= 0) to 4.5 K(x=0.04).[34]In addition, experiments show that theTcof WTe2can be increased to 7 K under an applied physical pressure of 16.8 GPa.[35]Moreover, manifold phase transitions from MI to metal show in 1T-TaS2thin flakes with collapses of CDWs,and finally SC are induced by ionic gating.[36]

Currently, CuIr2Te4, adopting a NiAs defected structure of trigonal symmetry with the space groupP-3m1, has been found to exhibit the coexistence of the CDW-like transition(TCDW= 250 K on heating and 186 K on cooling) and SC(Tc= 2.5 K). Besides, recent electronic structure calculations have unveiled that the Fermi energy is mostly derived from Ir 5d and Te 5p orbitals.[39]More recently, experiments have documented that both CDW and SC performances of CuIr2Te4can be modified via 3d, 4d transition metals (e.g.,Ti and Ru) and 4p, 5p dopants (e.g., Se and I). Dome-shape phase diagrams with respect toTcvs. doping amount associated with the suppression of CDW have been found in the CuIr2-xRuxTe4and CuIr2-xTixTe4systems, but dome-shape diagrams crowded in the middle doping region with two CDW regions at two sides in Se- and I-doped systems.[40-43]Furthermore, the non-magnetic element Al is usually selected as the dopant because Al3+ion has a closed shell electron configuration and a clear oxidation state. The transport properties of Al-doped high-Tccopper-based superconductors (e.g.,SmBa2Cu3-xAlxO6+δ, YBa2Cu3-xAlxO7) have been widely studied.[44,45]And nano Al has been used to improve the critical current in MgB2superconductor.[46]Therefore,it will be interesting to explore the effect of 3s dopants(e.g.,Al)on the CDW and SC in CuIr2Te4.

In this work,we prepared polycrystalline CuIr2-xAlxTe4(0 ≤x≤0.2) compounds successfully by a solid-state reaction method. Our results demonstrate that the CDW order can be completely suppressed within a fine-tuned Al-doped content as a result of the improvement ofTc.Tcinitially increases with the rise of doping amount untilx=0.075 and reaches the highest value of 2.75 K, eventually forming a dome-phase like electronic phase diagram. The acquisition of the CuIr2-xAlxTe4(0 ≤x≤0.2)system also provides some enlightenment for the search of new superconductors.

2. Experimental methods

Synthesis Polycrystalline specimens of CuIr2-xAlxTe4(0 ≤x≤0.2) were prepared through the classical solidstate phase reaction. First, the Cu (99%, Alfa Aesar), Ir(99.9%, Macklin), and Al (99.95%, Aladdin) powder, and Te lump (99.999%, Alfa Aesar) with an element ratio of Cu:Ir:Al:Te=1:2-x:x:4.05 were sealed in quartz tubes,then they were put in a muffle furnace with the ramping rate of 1°C/min to 850°C and the furnace temperature was maintained for 5 days. The resulting samples were annealed at 850°C for 4 days with a heating rate of 1°C/min.

Instruments Powder x-ray diffraction(PXRD)MiniFlex,Rigaku with CuKα1radiation was used to examine the crystal structure and phase purity of the CuIr2-xAlxTe4(0 ≤x≤0.2)compounds.FULLPROF software suite was used to determine the cell parameters based on Thompson-Cox-Hastings pseudo-Voigt peak shapes model. Measurements of the temperaturedependence of electrical resistivity, specific heat, and magnetic susceptibilities (M(T,H)) were performed by a Dyna-Cool Quantum Design physical property measurement system(PPMS,Quantum Design,Inc.).

3. Results and discussion

The PXRD patterns of the CuIr2-xAlxTe4compounds are presented in Fig. 1(a). PXRD analysis shows that Al concentration is limited up to 0.2 since Al2Te3impurity is found with further increasing Al content. As Al doping content increases, the (001) peak moves to the right,which can be verified by the decrease of lattice constantsaandcwith increasingx(Fig. 1(c)), reflecting the compression of the CuIr2Te4unit cell. As illustrated in Fig. 1(c)clearly, both lattice constants (aandc) andc/asingly reduce with increasing Al concentration. It is found thataandcreduce from 3.9397(5) °A and 5.3965 (3) °A for the pristine sample to 3.9264(1) °A and 5.3757(2) °A (x= 0.2) in CuIr2-xAlxTe4, respectively. The detailed refinement of the selected sample CuIr1.925Al0.075Te4is displayed in Fig. 2(a).Most of the diffraction peaks have been indexed in terms of trigonal symmetry with a space groupP-3m1 (No. 164)and some small peaks indexed for tiny unreacted Ir are also detected. The illustration shows that the disordered trigonal structure, in which the Cu is inserted between twodimensional(2D)IrTe2layers,Ir partial substituting by Al simultaneously(see Figs.2(b)and 2(c)).

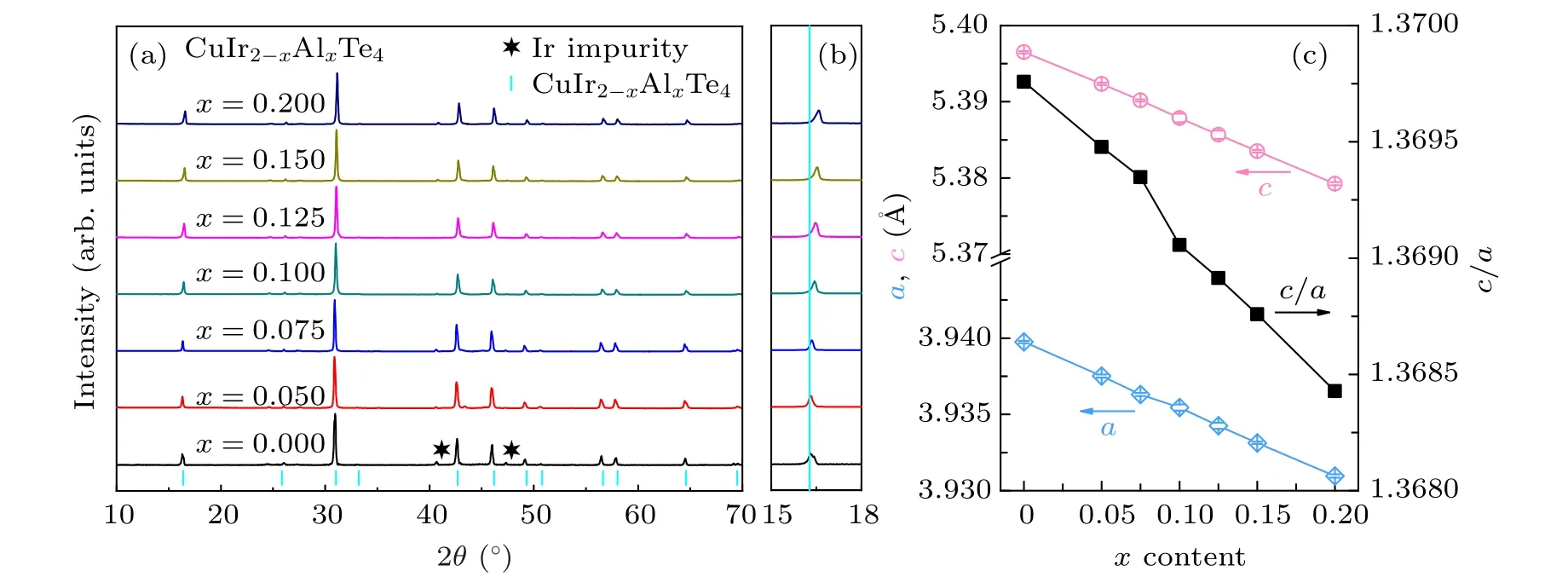
Fig.1. (a)and(b)PXRD patterns of the CuIr2-xAlxTe4 (0 ≤x ≤0.2)compounds. (c)The evolution of lattice constants for CuIr2-xAlxTe4 (0 ≤x ≤0.2).

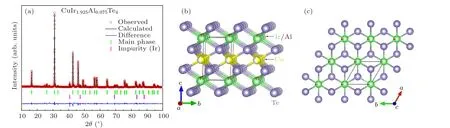
Fig.2. (a)Refinements of CuIr1.925Al0.075Te4 polycrystalline sample. (b)and(c)The crystal structure of CuIr2-xAlxTe4 in different direction views.

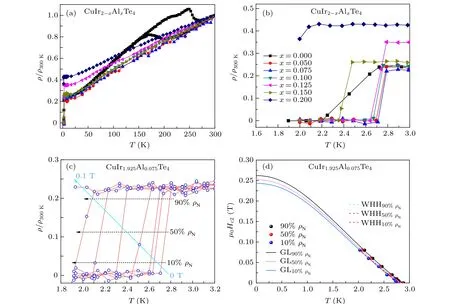
Fig. 3. (a) Temperature-dependence of resistivity for the polycrystalline CuIr2-xAlxTe4 (0 ≤x ≤0.2) compounds. (b) The superconducting transition at 1.6-3.0 K for the polycrystalline CuIr2-xAlxTe4 (0 ≤x ≤0.2) compounds. (c) Temperature dependences of resistivity for the polycrystalline CuIr1.925Al0.075Te4 sample under various applied magnetic fields. (d)Temperature dependence of Hc2 for the polycrystalline CuIr1.925Al0.075Te4 sample.

The temperature-dependent normalized resistivity(ρ/ρ300K) of the CuIr2-xAlxTe4(0 ≤x≤0.2) compounds is exhibited in Fig. 3(a). Besides, our previous finding indicates that there is no structure transition for the pristine sample. Thus,we propose that the normalized resistivity with cooling and heating exhibits a distinct hysteresis associated with the formation of CDW-like transition for the pristine CuIr2Te4sample. It is worth mentioning that no signature of the abnormal hump can be observed aboveTcinρ/ρ300Kof the Al doping samples CuIr2-xAlxTe4(0＜x≤0.2), indicating the CDW-like transition can be suppressed with subtle Al substitution for Ir,companying with the increment ofTc. The resistivity data for Al-doped samples show a metallic behavior.We can observe sharp drops ofρ(T) for the CuIr2-xAlxTe4(0 ≤x≤0.15) below 3.0 K (see Fig. 3(b)), which represent the outset of the superconducting state. The transition width of the Al-doped compounds is much narrower than that of the pristine CuIr2Te4. TheTcand residual resistivity ratio (RRR=R(300 K)/R(3 K))of the CuIr2-xAlxTe4(0 ≤x≤0.2)samples are summarized in Table 1. As the Al content increases,bothTcand RRR increase to the highest value atx=0.075,then decrease for further Al doping. For 0.075 ≤x≤0.5,the RRR sharply decreases form 4.44 forx=0.075 to 2.342 forx=2.34. This phenomenon indicates that high Al content induces significant disorder in the polycrystalline CuIr2-xAlxTe4series.

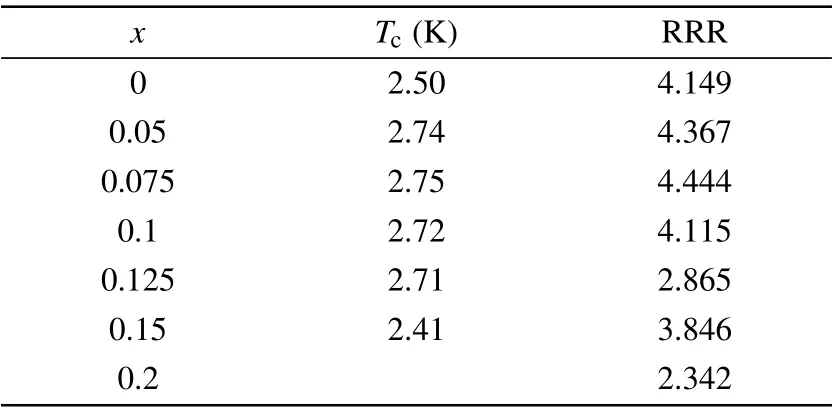
Table 1. The Tc and RRR of CuIr2-xAlxTe4 (0 ≤x ≤0.2)compounds.The Tc is determined by using 50%normal state resistance criterion.

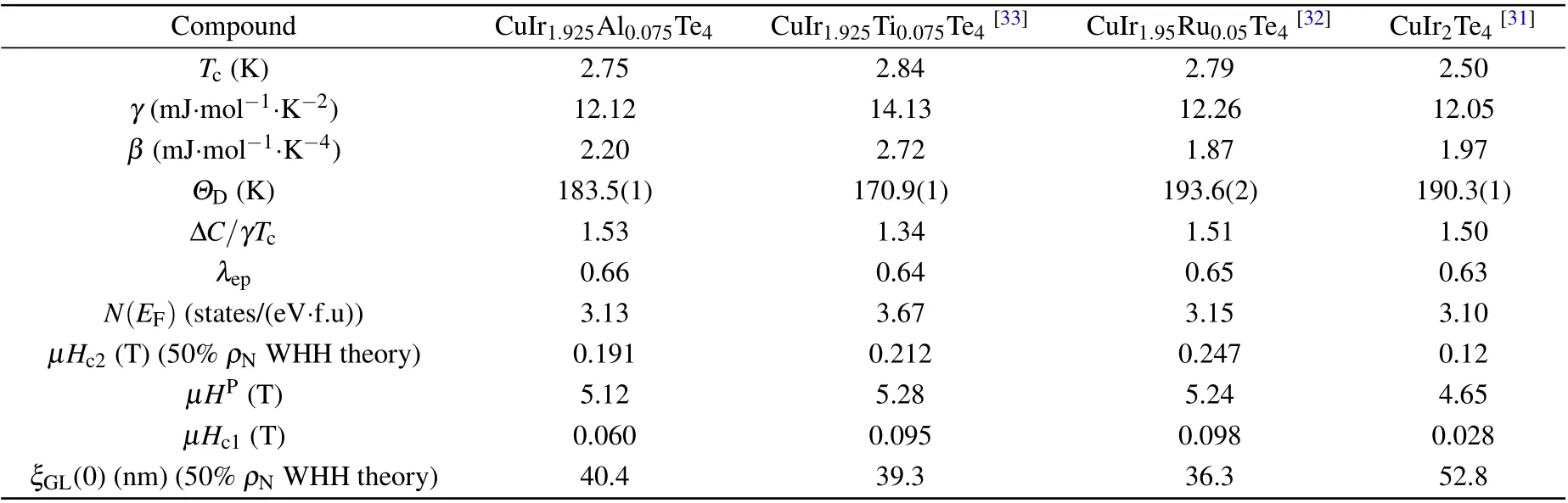
Table 2. Comparison of physical properties of CuIr2Te4-based superconductors.

The superconducting transition has also been confirmed by the magnetic susceptibility data(Fig.4(a))with strong diamagnetic signals under zero-field-cooling (ZFC) mode. The superconducting volume fraction of the CuIr2-xAlxTe4(0 ≤x≤0.15) compounds can be calculated around 95%, which manifests high purity of the polycrystalline CuIr2-xAlxTe4samples. Next, we examine the lower critical fields (μHc1)by the field-dependent magnetic susceptibilityM(H)measurements in a temperature range of 2-2.6 K.Figure 4(b)presents the magnetization(M-H)curves at different temperatures belowTcof the representative CuIr1.925Al0.075Te4. As shown by the purple line in Fig. 4(b), theM(H) isotherms show a linear relationship with the magnetic field (H) at low magnetic fields,indicating that it is a type-II superconductor.We can extract the demagnetization factor(N)following the expressionN=4πχV+1, whereχV= dM/dHrepresents the linearly fitted slope. The calculatedNfor CuIr1.925Al0.075Te4is about 0.53. We can use the expressionMfit=m+nHto fit the experimental data at low magnetic fields,wheremrepresents the intercept andnstands for the slope of linear fitting from the low magnetic fieldM(H)data. The inset of Fig.4(c)displays the (M-Mfit) data vs.H. Then, we can fit theμHc1(T) by the expressionμ0Hc1(T)=μ0H*c1(T)/(1-N), whereμ0H*c1is the intersection point between theM-Mfitvs.Hcurves and the field (purple line in the inset of Fig. 4(c)), which deviates by～1% above the fitted data (Mfit) as customary. The temperature dependence ofμ0Hc1(T) for CuIr1.925Al0.075Te4is displayed in the main panel of Fig. 4(c). Consequently,we can further acquire theμ0Hc1(T) using the equationμ0Hc1(T)=μ0Hc1(0)(1-(T/Tc)2). The estimatedμ0Hc1(0)at zero temperature of CuIr1.925Al0.075Te4sample is 0.060 T,which is larger than that of the undoped parent sample (see in Table 2).

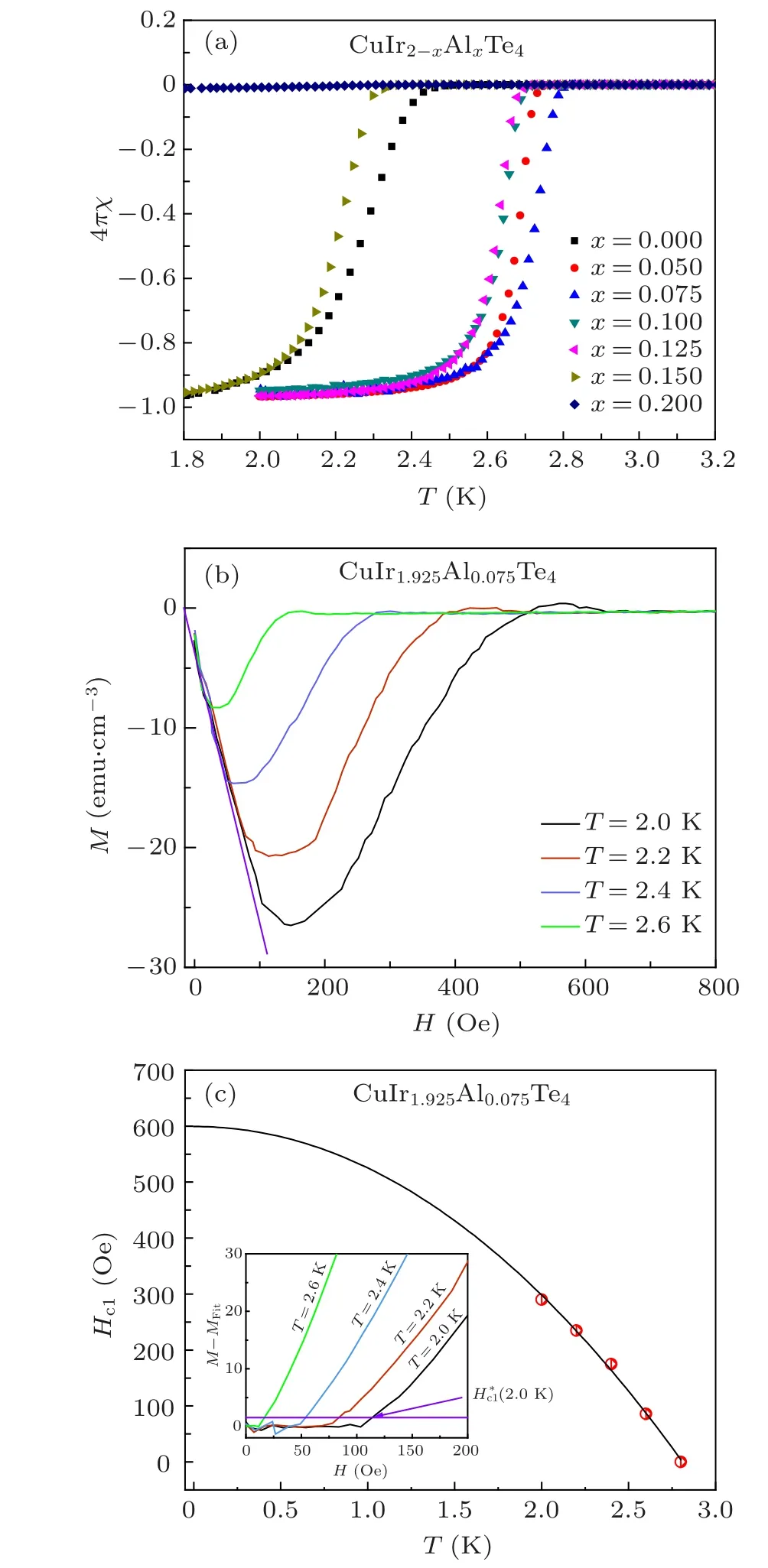
Fig. 4. (a) Magnetic susceptibility for CuIr2-xAlxTe4 (0 ≤x ≤0.2) compounds under 30 Oe magnetic field with zero-field-cooling (ZFC) mode.(b) The magnetization M(H) in a temperature range of 2-2.6 K for CuIr1.925Al0.075Te4. (c) Temperature dependence of Hc1. Inset: Difference between M and MFit in a temperature range of 2-2.6 K for CuIr1.925Al0.075Te4.

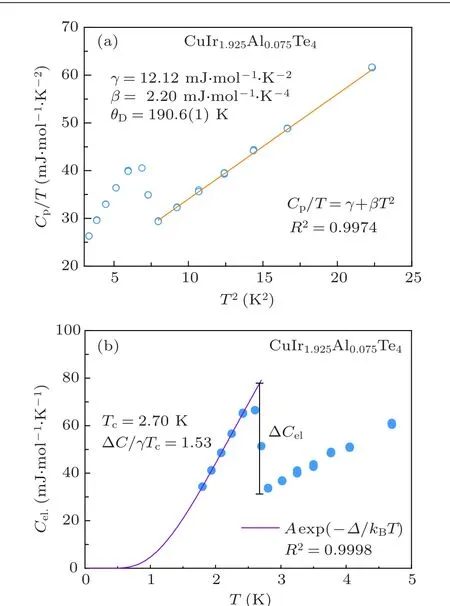
Fig. 5. (a) The specific heat data plotted as a function of T2 for CuIr1.925Al0.075Te4. (b) The electronic part of the specific heat in CuIr1.925Al0.075Te4.

To further convince that SC is an essential feature of the highestTccompound CuIr1.925Al0.075Te4,we also perform the temperature-dependent specific heat measurement. Figure 5 illustrates the detailed characterization of the superconducting transition in the highestTccomposition CuIr1.925Al0.075Te4through specific heat measurements under the absence of magnetic field. The dataCp/Tvs.T2can be fitted by the equationCp=γT+βT3above theTcto acquire the values ofβandγbeing 2.20 mJ·mol-1·K-4and 12.12 mJ·mol-1·K-2for CuIr1.925Al0.075Te4,respectively,whereγTrepresents the sum of electron contributions(Cel.)to the specific heat andβT3is the sum of phonon contributions(Cph.). Figure 5(b)shows the sum of electron contribution to the specific heat at the temperature near theTcunder 0 T, whereCel.is easily derived from deducting the phonon part,Cel.=Cp-βT3. Apparently, a sharp specific heat jump occurs in our representative CuIr1.925Al0.075Te4, characteristic of bulk SC. TheTcfurther can be determined to be 2.70 K using the common equal-area entropy construction method,which agrees well with those observed in magnetization and resistivity tests. Based on theTcandγvalues, we can determine ΔCel./(γTc)=1.53, which is slightly larger than the value of 1.43 forecasted by the BCS theory,revealing its superconducting nature. The Debye temperature obtained using the equationΘD=(12π4nR/(5β))1/3is 183.5(1)K,whereRrepresents the gas constant,nexpresses the number of atoms per formula unit. The resultant electronphonon coupling constantλepvalue further estimated by introducing theΘDnumber into the inverted McMillan equation[49]

Finally, to further understand the effect of Al dopant on the CDW and SC of CuIr2Te4, the electronic phase diagrams plotted asTcversus Al-contentxhave been established (see Fig.6).All theTcvalues were obtained from the resistivity and magnetization tests.From Fig.6,we can find that the CDW order is immediately suppressed whileTcincreases with increasing Al content up tox=0.075 and rises towards the highest value 2.75 K atx=0.075. From this,we find that despite subtle Al is substituted for Ir,it has a strong impact on the SC and CDW. Besides, in contrast to our previously reported Ru/Tidoped CuIr2Te4system,the similarity is the destabilization of CDW upon small amount doping concentration no matter Ru,Ti,or Al as dopants and formation of dome-shape like superconducting phase diagrams.[32,33]Despite overall similarities,there are significant differences between the CuIr2-xRuxTe4,CuIr2-xTixTe4,and CuIr2-xAlxTe4systems. Substitution of Ir by Ru or Ti in CuIr2Te4corresponds to a“hole”(p-type)doping of the IrTe2layers, while partial doping Al into Ir site in CuIr2Te4is an electron (n-type) doping. As for the high-Tccuprate superconductors,where the competition between antiferromagnetism and SC develops as a function of chemical doping,the evolving balance between competing electronic orders in CDW/SC systems is one of their most fundamentally tempting properties. In our case, the bands in the neighborhood of the Fermi energyEFof the pristine sample CuIr2Te4mostly come from Ir d and Te p orbitals and locate at a flat plateau,in which Al doping acts as a chemical pressure,closing the gap on the Fermi surface that usually leads to rapid suppression of CDW.On the other hand,the increase of band filling of the Fermi surface under chemical pressure could be the mechanism of the promotion of SC.But further study and evidence need to be collected to find out the competition between CDW and SC.

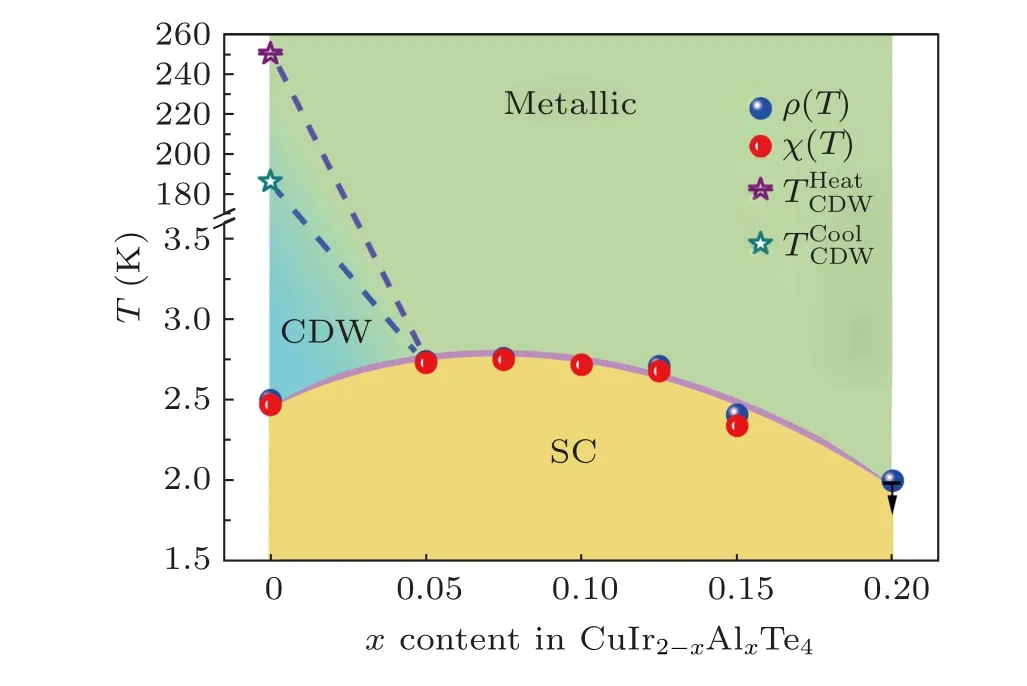
Fig. 6. The electronic phase diagram of polycrystalline CuIr2-xAlxTe4(0 ≤x ≤0.2)series.

4. Conclusion and perspectives

In conclusion, we have successfully synthesized a series of polycrystalline CuIr2-xAlxTe4(0 ≤x≤0.2) samples via a solid-state method and systemically studied the effect of Al doping on the structure and electronic properties of CuIr2Te4. The ΔCel./(γTc)=1.53 for the highestTcsample CuIr1.925Al0.075Te4is slightly larger than 1.43 (BCS value),proving its bulk superconducting nature. We recognize that the CDW order is suppressed immediately whileTcincreases as Al doping amountxrises and achieves a maximumTc=2.75 K with Al doping content of 0.075. Our systematic study of CuIr2-xAlxTe4(0 ≤x≤0.2) not only extends the family of the TMD superconductors but also provides a platform for further research on the relationship between the CDW and SC.

Acknowledgments

H. X. Luo acknowledges the financial support by the National Natural Science Foundation of China (Grant No. 11922415), Guangdong Basic and Applied Basic Research Foundation, China (Grants No. 2019A1515011718),and the Pearl River Scholarship Program of Guangdong Province Universities and Colleges (Grants No. 20191001).Y. Zeng and D. X. Yao are supported by the National Natural Science Foundation of China (Grants No. 11974432)and the National Key R&D Program of China (Grant Nos. 2018YFA0306001 and 2017YFA0206203). D. Yan acknowledges the financial support by the National Key Laboratory Development Fund (No. 20190030). Y. H. Wang would like to acknowledge partial support by the National Key R&D Program of China (Grant No. 2017YFA0303000), National Natural Science Foundation of China (Grant No. 11827805),and Shanghai Municipal Science and Technology Major Project, China (Grant No. 2019SHZDZX01). M. Wang was supported by the National Natural Science Foundation of China(Grant Nos.11904414 and 12174454)and the National Key R&D Program of China(Grant No.2019YFA0705702).