Entanglement spectrum of non-Abelian anyons
2022-03-12YingHaiWu吴英海
Ying-Hai Wu(吴英海)
School of Physics and Wuhan National High Magnetic Field Center,Huazhong University of Science and Technology,Wuhan 430074,China
Keywords: fractional quantum Hall effect,anyons,entanglement spectrum,topological order
1. Introduction
Fractional quantum Hall (FQH) effect is a triumphy of emergence caused by strong correlation between particles. It was originally observed in two-dimensional electron gases exposed to an external magnetic field,[1]and its nontriviality has motivated extensive efforts to search for them in other systems.[2-7]The single-particle eigenstates of charged particles in magnetic field form Landau levels. If one Landau level is only partially filled, there would have been a macroscopic number of degenerate many-body states, but interactions between the particles generate incompressible gapped states at certain filling factorν(i.e.,the number of particles divided by the number of single-particle states per Landau level). This process cannot be understood using perturbative calculations and the theoretical elucidation has relied greatly on trial wave functions.[8-12]
The intricate pattern of correlation in FQH states goes beyond the Landau paradigm that characterizes phases of matter through symmetry breaking and local order parameter. It is perfectly possible for two FQH states to have the same symmetry but different physical properties. The elementary excitations of FQH states are fractionalized in the sense that their quantum numbers are fractions of the underlying particles. The braiding statistics of these fractionalized excitations are anyonic due to the special topological structure of twodimensional space.[13-15]This makes them different from the well-known bosons and fermions.If FQH states are defined on closed manifolds with non-zero genus, there would be multiple degenerate ground states in the thermodynamic limit.[16]This fact motivated the concept of topological order.[17]While the bulk of an FQH state is gapped,gapless excitations can be found in the vicinity of the edge,which provides a window for probing the topological properties.
One particularly interesting FQH state is the Moore-Read Pfaffian state as it supports anyons with non-Abelian braiding statistics.[12]If a few anyons are present at fixed positions in a system,it is still possible to have multiple degenerate states.When two anyons are exchanged,the system undergoes a unitary rotation in the degenerate subspace. This property is robust under local perturbations and may be used to perform fault tolerant quantum computation tasks.[18,19]On the experimental side, the Moore-Read construction may be relevant to the exotic state at filling factor 5/2.[20]A number of experiments have provided evidence[21-25]that the 5/2 state is described by the Moore-Read Pfaffian state, its particle-hole conjugate,[26,27]or the particle-hole symmetric version.[28-30]Besides the solid state platforms, the bosonic Pfaffian state may be realized for bosons in artificial magnetic field atν=1(Refs.[31-34])or in chiral spin liquids.[35-39]
It is very much desriable to extract as much information as possible from a trial wave function. A useful tool in this regard is the entanglement spectrum.[40]The system under consideration is divided into two subsystems,and the reduced density matrix of one subsystem can be computed for a given state. It is written as exp(-Hent)withHentdubbed the“entanglement Hamiltonian”and its eigenvalues comprise the entanglement spectrum. If the system realizes an FQH ground state and the cut is performed in orbitals or real space, the entanglement spectrum mimics that of the edge modes. One may further introduce anyons on top of the FQH ground state,and their presence alters the entanglement spectrum.[41]
In this paper,we study the entanglement spectrum of two or four anyons of the bosonic Moore-Read state. The elementary anyon obeys non-Abelian Ising braid statistics, and two of them may fuse to an identity state or a neutral fermion state. The counting of levels in the entanglement spectrum are affected by the number of anyons enclosed in the subsystem and how they fuse together. The quasihole states are relatively easy to understand because parent Hamiltonian and conformal field theory techniques are available,but the quasiparticle states are much more difficult. Based on a bipartite representation of the Moore-Read state, quasiparticle wave functions have been proposed using the composite fermion theory.[42-44]The energetics and overlaps of them turn out to be reasonably good, but it is unclear if they have the desirable topological properties. This issue shall be addressed below. In Section 2,the trial wave functions for these excitations are introduced and some details about computing the entanglement spectrum are explained. The RSES of these cases are presented with a detailed discussion in Section 3, we summarize the paper in Section 4.
2. Models and methods
Trial wave functions for FQH states are usually written on the infinite plane with symmetric gaugeA=B(-x,y,0)/2.The plane can be parameterized by the complex coordinatez=x+iy,and the single-particle wave functions in the lowest Landau level(LLL)has the simple formφ0m(x,y)~zme-|z|2/4(apart from a normalization factor). The ubiqutous Gaussian factor can be omitted in most cases, which ensures that a many-body wave function in the LLL is an analytic function of thez’s. The wave functions on higher Landau levels involve the associated Laguerre polynomial, but we shall not use them explicitly in this paper. In numerical calculations,the spherical geometry(see Fig.1 for an illustration)has been widely employed due to its compactness.[9]The magnetic field through the surface of the sphere is generated by a magnetic monopole at the center of the sphere. The single-particle wave functions are labeled by three parametersQ,l,m,where 2Qis the strength of the magnetic monopole,lis the total angular momentum,andmis thezcomponent of the angular momentum.The Landau level indexαis related to them vial=Q+αand the number of orbitals in theα-th level is 2Q+2α+1. In our subsequent discussions, we shall useQ+mto label the single-particle orbitals since it is an integer whilemcould be an half integer.
The Moore-Read ground state wave function for bosons atν=1 is[12]

where the number of bosonsNshould be even andPfdenotes the Pfaffian of an antisymmetric matrix. It was obtained as the correlation function of vertex operators of boson fields and Majorana fields in a conformal field theory. Another interpretation is based on the analogy with superconductors.[45-47]The Jastrow factor ∏Ni<j(zi-zj) attaches magnetic fluxes to the bosons so they become composite fermions, which form a chiral p-wave paired state described by the Pfaffian factor.The wave function Eq. (1) is the highest-density zero-energy eigenstate with respect to the parent Hamiltonian

This type of quasihole is denoted asσand their fusion rule isσ×σ=I+ψ, whereIis the identity state andψis the neutral fermion state.[49-51]The fusion result of the two quasiholes in Eq.(3)is the identity state. In the chiral p-wave pairing description, the neutral fermion state corresponds to one unpaired composite fermion as the Bogoliubov´ee Gennes theory of superconductivity would predict.
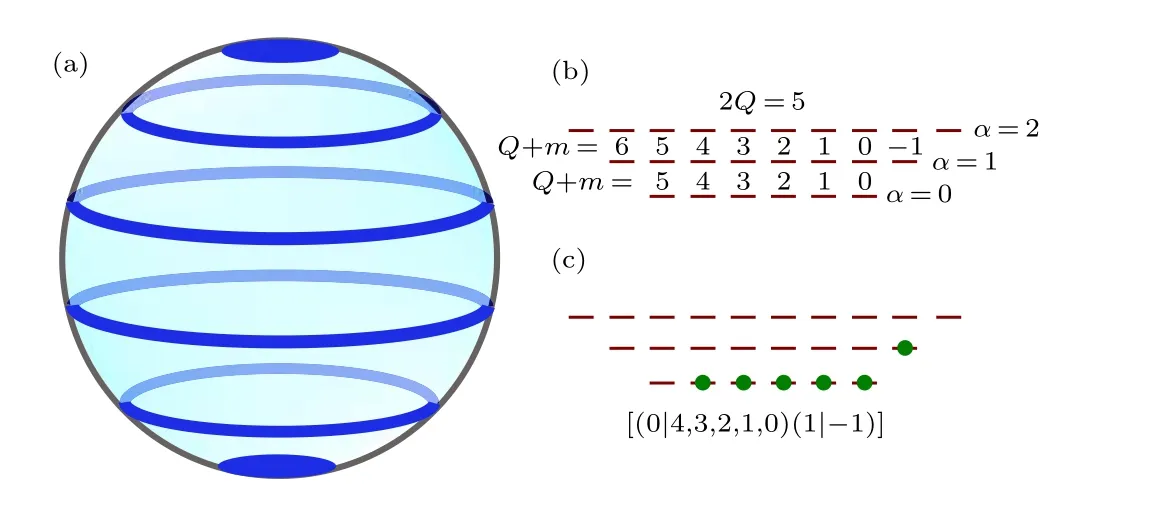
Fig. 1. Schematics of the single-particle orbitals on the sphere. (a) The orbitals are localized along the azimuthal direction. (b)The number of orbitals in the α-th level is 2Q+2α+1 and the range of Q+m is[-α,Q+α]. (c)An occupation labaled as[(0|4,3,2,1,0)(1|-1)].
To understand the quasiholes and quasiparticles on an equal footing, we need to transform the Moore-Read state to a bipartite form and use the composite fermion theory.[42-44]The first step is to rewrite the Moore-Read ground state as

The particles are divided into two groups called“pseudo layers”,Sis a symmetrization operator acting on the possible divisions into these two groups,and the coordinates{z}are relabeled as{v1,v2,...}and{w1,w2,...}.It is easy to recognize that the two factors inside the bracket are the Laughlin ground state wave function for bosons atν=1/2.[8]The connection between Laughlin and Moore-Read states actually goes beyond the ground state. The wave function with two quasiholes can be expressed in a bipartite form as

where the two factors are Laughlin states with one quasihole.This motivates us to speculate that other excitations of the Moore-Read state can also be constructed using the excitations of the Laughlin state.
A unified framework for the excitations of the Laughlin state is provided by the composite fermion (CF) theory. To begin with,we rewrite the Laughlin ground state as

The second factor performs flux attachment on the bosons to turn them into composite fermions, which experience a reduced magnetic field and they form their own Landau-like levels. As a first-order approximation, the composite fermions can be taken as non-interacting. The first factor indicates that the Laughlin ground state emerges if the composite fermions form theν=1 integer quantum Hall (IQH) state. The excitations of the FQH state are mapped to the excitations of the IQH state of composite fermions. If all but one orbitals in the zeroth CF level are occupied, we recover the Laughlin state with one quasihole described above. The success of this approach is further corroborated by the quasiparticle wave functions it produce.[52]For example, if the zeroth CF level are fully occupied and one composite fermion is placed in the first CF level, the resulting state would be a Laughlin state with one quasiparticle. To describe general CF configurations succinctly, the state with composite fermions in the orbitalsm01,m02,...,m0N0of the zeroth level and the orbitalsm11,m12,...,m1N1of the first level would be labeled as[(0|m01,m02,...,m0N0)(1|m11,m12,...,m1N1)]. The bipartite representation of the Moore-Read state can be generalized to

withχ1({v}) andχ2({w}) being two CF states. In particular,if they correspond to Laughlin states with excitations,Ψbpwould be a Moore-Read state with some excitations. It has been verified in numerical calculations that this prescription indeed provides very good approximations.[42-44]For a given combination ofNand 2Q, the low-energy bipartite CF states are constructed as follows. The number of bosons in the two pseudo-layers are denoted asNvandNw. IfNis even,we haveNv=Nw=N/2. IfNis odd,we chooseNv=(N+1)/2 andNw=(N-1)/2. The monopole fluxes in both pseudo layers are the same as 2Q. The problem is thus reduced to that of finding the low-energy states ofNvandNwbosons in 2Qfluxes,which are nothing but various excitations around filling factor 1/2. The effective monopole fluxes for the composite fermions are denoted as 2Q*v=2Q-Nvand 2Q*w=2Q-Nw.The CF configuration of each pseudo layer is chosen such that the effective kinetic energy is minimized. In many cases,this constraint alone does not generate a unique CF state, and we shall select certain states with excitations localized around the two poles. This can be achieved easily because the singleparticle orbitals are localized along the azimuthal direction.The composite fermions are added or removed successively starting from the orbitals with the largest or smallestQ+mtowards the equator.
The entanglement spectrum can be computed for any given many-body state|Ψ〉. The Hilbert space of the system is divide into two partsAandB, the reduced density matrix of partAis obtained by tracing out the subsystemB, and the eigenvalues ofρAare expressed as exp(-ξi). Theξi’s are plottedversusthe good quantum numbers of the subsystemAto produce the entanglement spectrum. The cut of the Hilbert space can be performed in orbital,[40]particle,[53]or real space,[54-56]which can reveal different aspects of topological properties. We study the real space entanglement spectrum(RSES)and chooseAto be the southern hemisphere.The good quantum numbers are the number of particles in regionA(denoted asNA) and thezcomponent of the total angular momentum of regionA(denoted asLzA). One characteristic of the edge physics of FQH states is the numbers of universal low-energy levels at different angular momentums. For example,the edge of the Laughlin state is described by the SU(2)1Wess-Zumino-Witten theory,and the counting of edge modes is 1,1,2,3,5,.... If one introduces quasiholes or quasiparticles into the bulk of the system(i.e., sufficiently far from the edge), the counting would not be affected because these excitations are Abelian anyons. It has been shown that these properties are faithfully reproduced in the entanglement spectrum on the sphere where the entanglement cut is viewed as an virtual edge.
3. Numerical results
Theν=1 bosonic Moore-Read ground state occurs at monopole fluxes 2Q=N-2 on the sphere. In subsequent discussions, we consider excitations on top of the systems withN= 18, 2Q= 16 orN= 20, 2Q= 18. The Moore-Read edge physics involves a chiral boson mode and a chiral Majorana fermion mode.[57-60]At sufficiently low energy, their dispersions can be taken as linear. The chiral boson mode is described by the Hamiltonian

wheregfis the mode velocity, the fermionic operatorcmsatisfies{cm,cn}=δm+n, and the angular momentummshould be integers(half-integers)if the fermions have periodic(antiperiodic)boundary conditions. The number of fermions is not conserved by this Hamiltonian,but its parity is conserved.The Hilbert space can be decomposed into four sectors labeled by the parity of the number of fermions and the boundary condition, and edge excitations can only be created in each sector separately. The final counting of edge states is the convolution of the bosonic and fermionic modes, which can be checked in numerical calculations. For a system in the ground state,the counting of edge states is 1,1,3,5,...(1,2,4,7,...)when the number of particles is even(odd). On the other hand,if aσquasihole or quasiparticle is introduced to the center of the system, the counting of edge state changes to 1,2,4,8,...regardless of the number of particles. The orbital entanglement spectrum of the ground state and certain states with excitations have been studied before,[41]and we shall perform a more indepth study of many other cases.
3.1. Quasiholes
We begin with the cases with two quasiholes. The counterpart of Eq.(3)on the sphere can be obtained if 2Qincreases by one whileNremains intact. The orbital entanglement spectrum of this kind of states has been studied in Ref.[41]. The RSES does not reveal fundamentally new insights, but it is helpful to revisit them within the bipartite framework. In the bipartite representation Eq. (5), these twoσquasiholes are separated to the two pseudo layers such that the two factors insideSof Eq.(7)are both Laughlin state with one quasihole.If one quasihole is placed at the south pole and the other at the north pole, the southern hemisphere would be a Moore-Read state trapping oneσquasihole at its center,so the counting of edge modes is 1,2,4,8,...for both even and oddNA.This expectation is confirmed by the RSES in Figs. 2(a) and 2(b). The RSES changes dramatically if both quasiholes are placed around the south pole as shown in Figs.2(c)and 2(d),
where the counting of levels is 1,1,3,5,...for evenNAand 1,2,4,7,...for oddNA. This means that the twoσquasiholes do not affect the topological properties of the southern hemisphere,so we conclude that they fuse to the identityI.
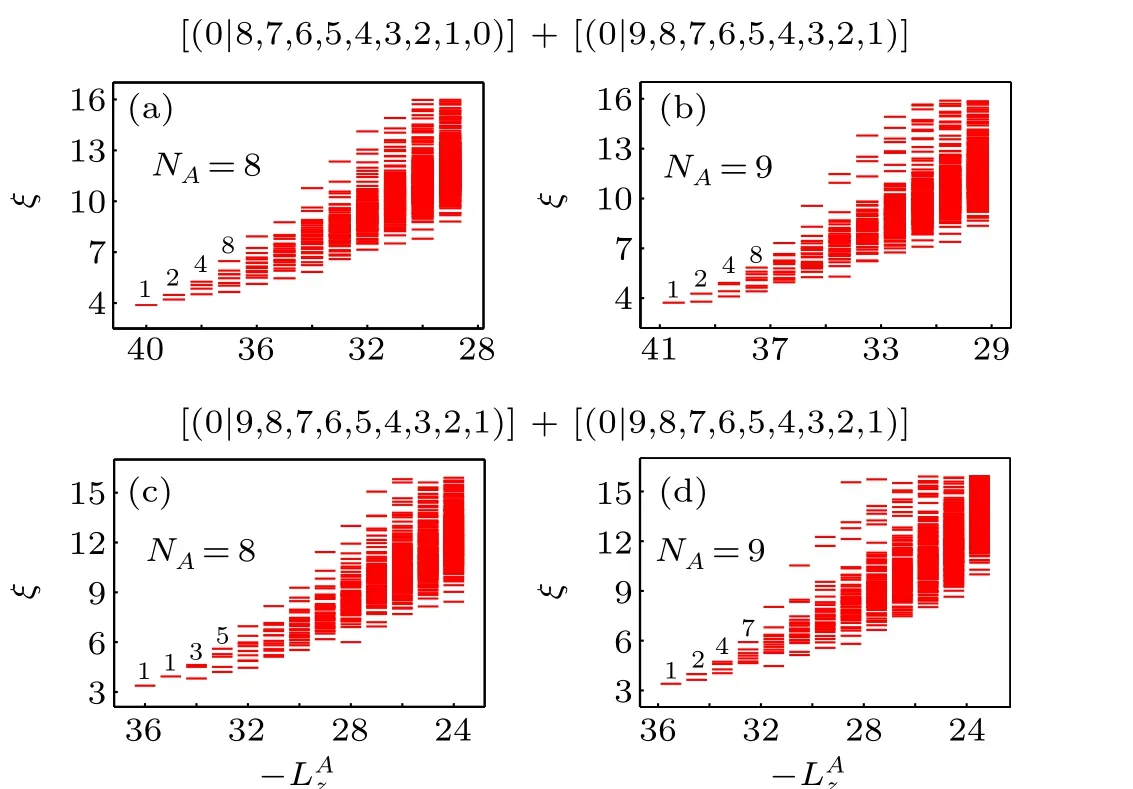
Fig. 2. RSES of the state with N =18 and 2Q=17. The system has two quasiholes and each pseudo-layer hosts one of them. The CF configurations of the pseudo-layers and the counting of levels are displaced. In panels (a)and (b), there is one quasihole near each pole. In panels (c) and (d), both quasiholes are near the south pole.

Fig. 3. RSES of the state with N =19 and 2Q=18. The system has two quasiholes and they are hosted by the same pseudo-layer. The CF configurations of the pseudo-layers and the counting of levels are displaced. In panels (a) and (b), there is one quasihole near each pole. In panels (c) and(d),both quasiholes are near the south pole.
The advantage of the bipartite construction becomes transparent in another case with two quasiholes. It is natural to ask what happens if we create two quasiholes in the same pseudo-layer. In other words,there is one Laughlin state with two quasiholes and one Laughlin ground state insideSof Eq.(7).This can be achieved if we simultaneously increase 2Qby two andNby one. To reveal the nature of such quasiholes,we place one quasihole at each pole and compute the RSES.As shown in Figs. 3(a) and 3(b), the counting of levels are 1,2,4,8,...for both even and oddNA. This agrees with the results in Figs.2(a)and 2(b),which demonstrates that the quasiholes created here are alsoσquasiholes. An obvious difference emerges in Figs.3(c)and 3(d)when both quasiholes are moved to the south pole. The counting of levels is 1,2,4,7,...for evenNAand 1,1,3,5,...for oddNA,which is exactly opposite to the previous cases in Figs.2(c)and 3(d). This can be understood as soon as we realize that the two quasiholes in the system fuse to the neutral fermionψ. Its presence affects the parity of the number of bosons,so the counting for even(odd)NAin this case agrees with that of odd(even)NAif the system is in the ground state.
After studying the properties of twoσquasiholes,we proceed to the cases with fourσquasiholes. If 2Qincreases by two whileNremains intact, fourσquasiholes would be created and each pseudo-layer hosts one Laughlin state with two quasiholes. For simplicity, we only consider the cases with twoσquasiholes around each pole. The bipartite construction allows us to trace the origin of these quasiholes and distinguish between two possible cases in which theσquasiholes around the south pole are from different pseudo-layers or the same pseudo-layer.Based on previous analysis,we expect that the twoσquasiholes around the south pole fuse to the identityIin the former case and the neutral fermionψin the latter case. The RSES for these cases are presented in Fig. 4.When the twoσquasiholes are from different pseudo-layers,the counting of levels is 1,1,3,5,...for evenNAin panel (a)and 1,2,4,7,...for oddNAin panel(b). This means that they indeed fuse to the identityIso the counting is the same as in the ground state. When the twoσquasiholes are from the same pseudo-layer, the counting of levels is 1,2,4,7,...for evenNAin panel(c)and 1,1,3,5,...for oddNAin panel(d).This can be explained as that they fuse to the neutral fermionψ, so the counting is exactly opposite to those in panels (a)and(b).
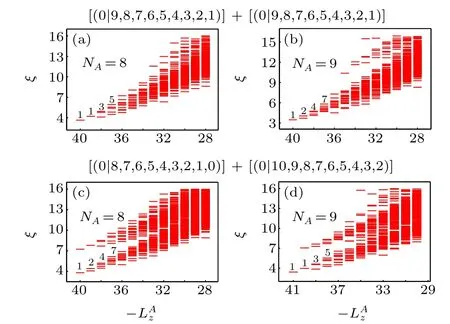
Fig. 4. RSES of the state with N =18 and 2Q=18. The system has four quasiholes and each pseudo-layer hosts two of them. The CF configurations of the pseudo-layers and the counting of levels are displaced. There are two quasiholes near each pole. In panels(a)and(b),the two quasiholes near the south pole are from different pseudo-layers. In panels (c) and (d), the two quasiholes near the south pole are from the same pseudo-layer.
3.2. Quasiparticles

Fig. 5. RSES of the state with N =18 and 2Q=15. The system has two quasiparticles and each pseudo-layer hosts one of them. The CF configurations of the pseudo-layers and the counting of levels are displaced. In panels(a)and(b),there is one quasiparticle near each pole.In panels(c)and(d),both quasiparticles are near the south pole.

Fig. 6. RSES of the state with N =19 and 2Q=16. The system has two quasiparticles and they are hosted by the same pseudo-layer. The CF configurations of the pseudo-layers and the counting of levels are displaced. In panels(a)and(b),there is one quasiparticle near each pole. In panels(c)and(d),both quasiparticles are near the south pole.
We now turn to the excited states with quasiparticles.The orbital entanglement spectrum of certain quasiparticle states have been studied in Ref.[41],where quasiparticles are trapped around the poles by adding local potentials to the exact parent Hamiltonian. In contrast,one highlight of this work is that we generate quasiparticle and quasihole states on an equal footing,which is very desirable from the aesthetic perspective.If 2Qdecreases by one whileNremains intact,two quasiparticles are created that are separated into the two pseudo-layers.If 2Qdecreases by two andNdecreases by one,two quasiparticles are created and they appear in the same pseudo-layer(the other pseudo-layer is in the Laughlin ground state). If 2Qdecreases by four whileNremains intact,four quasiparticles are created and each pseudo-layer hosts one Laughlin state with two quasiparticles. The RSES of these states are presented in Figs.5-7,which reveal identical physical insights as those in the previous subsection. Firstly, by comparing Figs. 5(a)and 5(b)with Figs.2(a)and 2(b),and Figs.6(a)and 6(b)with Figs. 3(a) and 3(b), we conclude that it is legitimate to call the quasiparticleσbecause it affects the counting of levels in the same way as theσquasihole. Secondly, twoσquasiparticles fuse to the identity state if they come from different pseudo-layers, as one can see from Figs. 5(c) and 5(d) and Figs. 7(a) and 7(b). Thirdly, twoσquasiparticles fuse to the neutral fermion state if they reside in the same pseudo-layer,as manifested by Figs. 6(c) and 6(d) and Figs. 7(c) and 7(d).Another nice feature of these spectra is that there are very few non-universal levels compared to those obtained using trapping potentials.

Fig. 7. RSES of the state with N =20 and 2Q=16. The system has four quasiparticles and each pseudo-layer hosts two of them. The CF configurations of the pseudo-layers and the counting of levels are displaced. There are two quasiparticles near each pole.In panels(a)and(b),the two quasiparticles near the south pole are from different pseudo-layers. In panels (c) and (d),the two quasiparticles near the south pole are from the same pseudo-layer.
4. Conclusion
To sum up,we have studied the RSES of the Moore-Read states with various anyons. The quasihole and quasiparticle are modeled on an equal footing usuing bipartite CF theory.The topological properties of these anyons are reflected by the counting of levels in the RSES. The presence of oneσquasihole or quasiparticle at the center of a system changes the boundary condition of the chiral Majorana fermions at the edge. The fusion results of two quasihole or quasiparticles can be predicted intuitively by inspecting their distribution in the pseudo-layers. The identity state of two quasiholes or quasiparticles does not affect the counting of levels in RSES, but the neutral fermion state leads to exactly opposite counting.The pseudo-layer structure also appears in other topological states. One noteable example is the Read-Rezayi Z3state with Fibonacci anyons,which is capable of universal topological quantum computation. The elementary excitations of this state have been constructed using the tripartite CF theory.[61]It would be interesting to study the entanglement spectrum of Read-Rezayi Z3state with multiple quasiholes/quasiparticles.This would be quite challenging because symmetrization over three pseudo-layer significantly increases computational time.The symmetrization method has been adopted in the tensor network framework to construct topological states,[62]and one may ask what properties can be extracted from entanglement spectrum in such cases. This work demonstrates that entanglement spectrum can be very useful in probing topological excitations,and we hope more investigations would be carried out along this line.
Acknowledgments
Project supported by the National Natural Science Foundation of China (Grant No. 11804107). The author thanks Hong-Hao Tu for helpful commments.
杂志排行
Chinese Physics B的其它文章
- Measurements of the 107Ag neutron capture cross sections with pulse height weighting technique at the CSNS Back-n facility
- Measuring Loschmidt echo via Floquet engineering in superconducting circuits
- Electronic structure and spin-orbit coupling in ternary transition metal chalcogenides Cu2TlX2(X =Se,Te)
- Characterization of the N-polar GaN film grown on C-plane sapphire and misoriented C-plane sapphire substrates by MOCVD
- Review on typical applications and computational optimizations based on semiclassical methods in strong-field physics
- Quantum partial least squares regression algorithm for multiple correlation problem
