Interrogation of optical Ramsey spectrum and stability study of an 87Sr optical lattice clock

Jing-Jing Xia(夏京京) Xiao-Tong Lu(卢晓同) and Hong Chang(常宏)

1CAS Key Laboratory of Time and Frequency Primary Standards,National Time Service Center,Xi’an 710600,China

2University of Chinese Academy of Sciences(CAS),Beijing 100049,China

Keywords: optical Ramsey spectrum,optical lattice clock,stability,coherence time

1. Introduction

Atomic clocks have developed rapidly due to advances in atoms,and optical and quantum science,[1,2]while research on atomic clocks has also promoted the development of scientific frontiers, affecting both basic and applied research. Nowadays, the time frequency standard plays a key role in many important fields, such as satellite navigation,[3]deep space exploration,[4]geodesy[5]and the verification of basic physical theory.[6,7]Thus, the optical clock based on optical frequency transition, which is at least four orders of magnitude higher than that of a microwave clock, has become the focus of time frequency standard research, as it can immensely improve the performance of the time frequency standard.[8]

The Ramsey spectrum plays a crucial role in the development of precise atomic spectroscopy, atomic clocks,quantum information processing[9-11]and research on optical clocks.[12,13]Compared with the Rabi spectrum,the Ramsey spectrum can reduce the linewidth by about half, with the same clock detection time, and is insensitive to inhomogeneous excitation. These advantages have resulted in it being widely applied to not only atomic frequency standards to improve stability,[14-16]but Bose-Einstein condensates,[17]quantum computing,[18]information processing[11]and research on the laws of quantum mechanics.[19,20]Recently,numerous theoretical and experimental studies of optical Ramsey spectrum have shown that the modified Ramsey spectrum can also improve the accuracy of optical clocks by sharply reducing the probe Stark shift by hyper-Ramsey spectrum or autobalanced Ramsey spectroscopy.[21-28]Surprisingly, there are few reports about the optical Ramsey spectrum in optical lattice clocks and few papers on detailed study of the stability in optical lattice clocks based on the Rabi or Ramsey spectra,although the optical Ramsey spectrum has been successfully applied in optical lattice clocks.[16]

In this paper, we experimentally demonstrate the optical Ramsey spectrum in an87Sr optical lattice clock using a twoπ/2-pulse excitation scheme.The coherence time and dephasing time between the clock laser and the lattice-trapped atoms are measured based on the optical Ramsey and Rabi spectra,respectively. Furthermore, we theoretically and experimentally compare the stability between Ramsey and Rabi detection with the same clock duty cycle (the ratio of clock detection time to clock cycleTc).

2. Experimental setup

After87Sr atoms are cooled to about 4 μK by two-stage laser cooling,[29]about 2.5×104atoms are trapped in a horizontal 1D lattice,which is formed by overlapping the linearly polarized incident and its retroreflector beams at the center of the cold atomic gas. To reduce the frequency noise and drift,the 813 nm lattice laser is stabilized to an ultra-low expansion(ULE)cavity by Pound-Drever-Hall(PDH)technique,as shown in Fig.1. Then,the lattice-trapped atoms are optically pumped into the1S0,mF=+9/2〉stretched state by employing the circularly polarized 689 nm laser and about 1.2×104atoms remain in the lattice after this process.

The clock transition of 5s21S0→5s5p3P0is interrogated by the linearly polarized clock laser at 698 nm,which is PDH stabilized to a 10 cm ULE cavity with a finesse of 400000.[30]The frequency and power of the clock laser are controlled by changing the frequency of the input radio-frequency signal and the diffraction efficiency of an acousto-optic modulator(AOM),respectively. The Rabi and Ramsey sequences are shaped by an AOM driven at a frequency of 190 MHz by an arbitrary function generator that enables fast and precise control of the intensity, frequency and phase of the clock laser. During the clock transition, along the direction of gravity, a bias magnetic field with a magnitude of 400 mG is applied to spilt the adjacent Zeeman sub-levels by about 47 Hz to resolve the ten Zeeman sub-levels.[31]This bias magnetic field also defines the quantization axis along the gravity direction and the polarization of the clock laser and lattice laser is parallel to the gravity direction to excite theπ-transition.

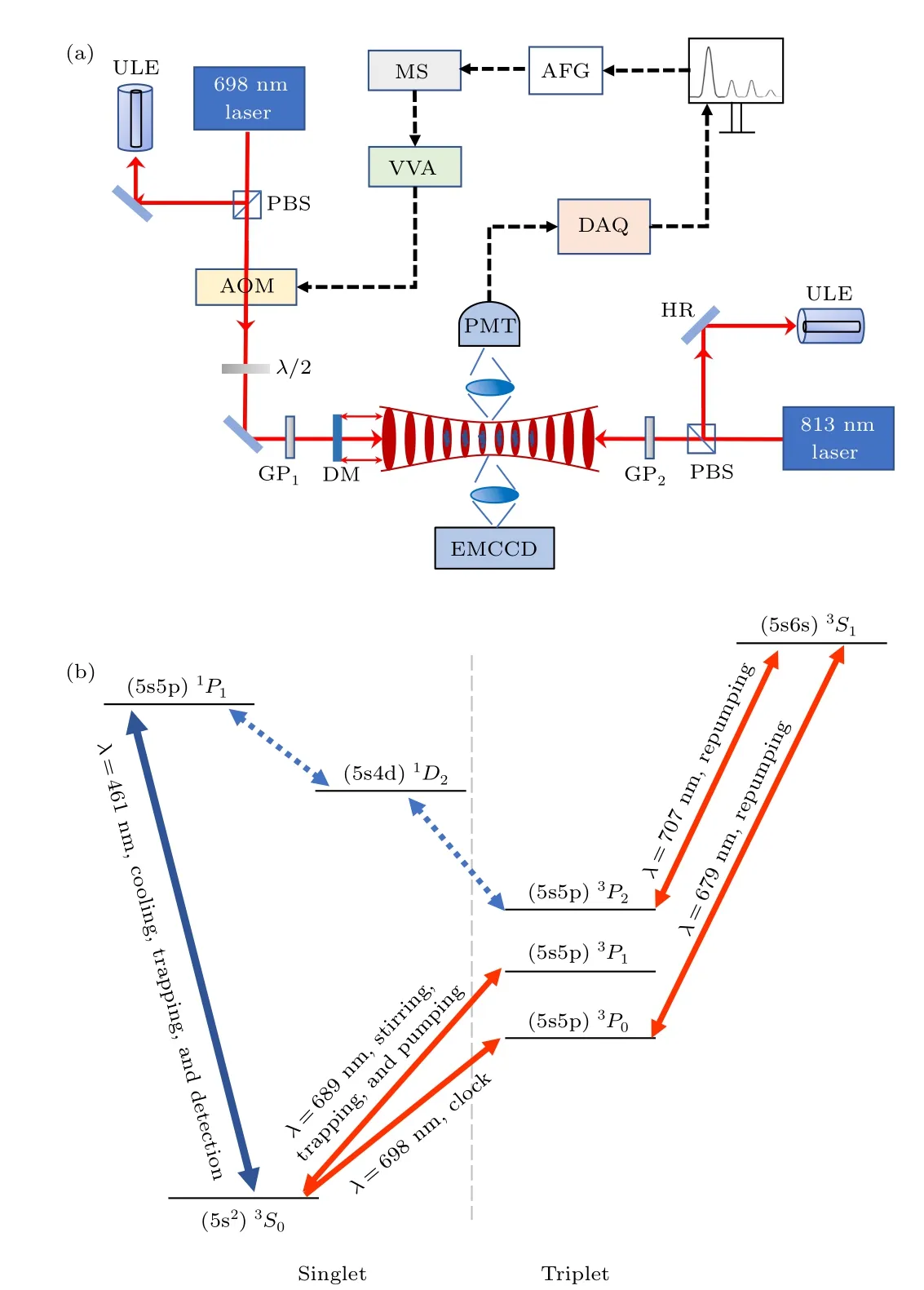
Fig. 1. Schematics of the experimental setup and energy levels. (a) Experimental setup of the lattice and the clock transition interrogation. AOM:acousto-optic modulator, AFG: arbitrary function generator, DAQ: data acquisition, MS: microwave switch, VVA: voltage variable attenuator, PMT:photomultiplier,HR:high reflector,GP1-2:Glan-Taylor polarizers,PBS:polarizing beam splitters,DM:dichroic mirror,λ/2:half-wave plate,EMCCD:electron multiplying charge-coupled device. (b)Energy-levels schematic of an 87Sr atom.

3. Results and discussion

3.1. Interrogation of the Ramsey spectrum

The interrogation scheme of the optical Ramsey spectrum with doubleπ/2-pulses is shown in Fig. 2(a). The firstπ/2-pulse creates a coherent state between the ground and excited states. Then, the clock laser is turned off and atoms go through a free evolution periodT,where the total wave function evolves with the atomic eigen energy and thus, a phase shift caused by the frequency difference between the clock transition and the clock laser accumulates.[9]The secondπ/2-pulse transfers the accumulated phase to the population difference between the1S0and3P0states,which allows effective measurement of the phase difference by detecting the excitation fraction. As there is no difference between the clock laser and the clock transition, the detected excitation fraction is at maximum. The optical Ramsey spectrum is obtained by scanning the clock laser frequency around the exact resonance and detecting the corresponding excitation fraction.

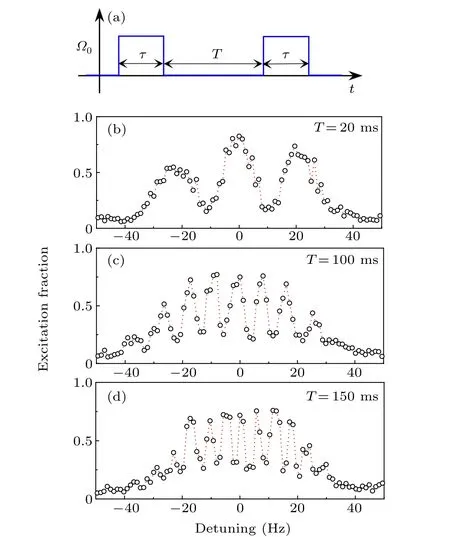
Fig.2. Experimental interrogation of the optical Ramsey spectrum. (a)Detection sequence of the optical Ramsey spectrum. (b)-(d) Optical Ramsey spectra at free evolution periods of 20 ms,100 ms,and 150 ms,respectively.

Figures 2(b)-2(d) experimentally interrogate the optical Ramsey spectrum,where the duration of theπ/2-pulses isτ=25 ms and the free evolution periodTis 20 ms, 100 ms, and 150 ms,respectively. With the increase inT,more Ramsey interference fringes are observed,and the difference between the maximum and minimum excitation fraction around the center of the Ramsey spectrum reduces. In terms of long free evolution periodT(when it exceeds 100 ms),the central Ramsey fringes are approximately sinusoidal.However,if the free evolution period is too long,the clock laser noise makes the interference fringes blurry,as shown in Fig.2(d). With the optical Ramsey spectrum,the Fourier-transform-limited full width at half maximum (FWHM) is ΔνRamsey≈1/(2(τ+T)), which is about half of the Rabi spectrum of ΔνRabi≈0.7987/TRaas the Rabi detection timeTRais equal to the Ramsey detection time of 2τ+T.[32]By sinusoidally fitting the central Ramsey fringe,the FWHM of Figs.2(b)-2(d)are 11.5(9)Hz,4.5(6)Hz,and 2.9(6)Hz, respectively,agreeing with the corresponding Fourier-transform-limited linewidths of 11.1 Hz,4 Hz,and 2.86 Hz,respectively.

3.2. Fringe contrast

The contrast C of Ramsey interference fringes can be defined as[33]

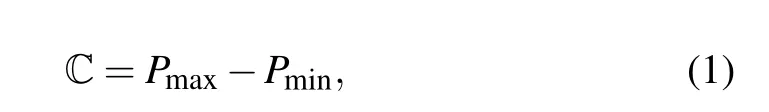
wherePmaxandPminindicate the highest and lowest excitation around the central Ramsey fringes,respectively. Thus,the frequency sensitivity of the Ramsey spectrum to the clock laser noises is proportional to C, indicating that higher stability is expected as the value of C is closer to 1.

As the number of interference fringes is below seven, C is obtained by only using maximum and minimum excitation of the central Ramsey fringe. When the free evolution period exceeds 100 ms, the fringes near the central Ramsey fringe will have a similar contrast, as shown in Figs. 2(c) and 2(d),and typically, the contrast is measured by the method shown in Fig. 3. Although the fringes of the Ramsey spectrum are blurry due to the noise of the clock laser,as the free evolution period is too long, contrast information can still be correctly extracted from the edges of the highest and lowest excitation fractions around the central interference fringes.

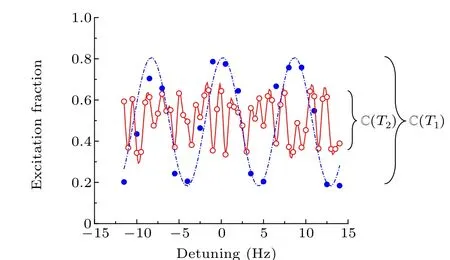
Fig. 3. Contrast measurement of the optical Ramsey spectrum. Circles are obtained with a free evolution period T1=120 ms and the dotted line represents the sinusoidal fitting. Hollow circles are obtained with a free evolution period T2=600 ms,and the red line indicates the direct connection of data as the clock laser noise washes out the sinusoidal nature of the fringes at such a long free evolution period(the sinusoidal fitting is unavailable in this case).Contrasts of C(T1)and C(T2)are extracted from the average floor and ceiling excitation fractions.

The contrast of the optical Ramsey spectrum is insensitive to the inhomogeneous excitation caused by thermal distribution of atoms in the lattice and the misalignment between the clock laser and lattice laser beams. However, atomic interaction, clock laser noises and inhomogeneous population between lattice sites can result in deterioration of the contrasts with the increase inT.[33]Figure 4(a)exhibits the Ramsey fringe contrast as a function of the free evolution period,where the 1/e Gaussian decay time of contrasts indicates the coherence time of the atom-light interactions.[34]The coherence time represents the maximum time of coherent control of the clock transition,which gives the maximum accessible free evolution period of the clock transition interrogation. By fitting the experimental data of Fig.4(a)with the Gaussian function, the coherence time is 340(23) ms.[34]Compared to the reported longest coherence time of 33(1)s,the coherence time in our system is mainly limited by the clock laser noise,atomic interaction and lattice light scattering.[34]At a Ramsey free evolution period that exceeds the coherence time,the Ramsey phase is randomized,which means that no useful phase information can be extracted from Ramsey detection,and thus,it is impossible to operate the clock.

In terms of Rabi detection, the maximum excitation also decreases with an increase in the clock laser duration, which is mainly caused by the inhomogeneous excitation. The 1/e decay time of the amplitude of the Rabi oscillation is called dephasing time. However, the interrogation is also coherent,even though the Rabi detection time exceeds the dephasing time and the Rabi oscillation will revive as long enough detection time.[35]Figure 4(b)displays typical Rabi oscillation,where the low clock laser intensity is used to accurately obtain the dephasing time. By fitting the “SineDamp” function of exp{-x/ω0}sin[Ω(x-x0)],dephasing time of 306(11)ms is extracted,which is consistent with the result obtained from decaying contrast data of Ramsey detection within its 1σuncertainty.Herein,x,Ω,ω0,andx0represent the clock laser duration,Rabi frequency proportional to the square root of clock laser intensity,dephasing time and shifting offset.

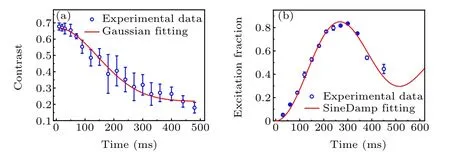
Fig.4. Measurements of the coherence time and dephasing time. (a)Ramsey fringe contrast as a function of free evolution period. (b)Excitation fraction of Rabi spectrum as a function of interrogation time. Red solid line of(a)is obtained by the Gaussian function fitting and the red solid line of (b) is the fitting with the amplitude exponential-decaying sinusoidal function. Error bars indicate 1σ standard deviation of five measurements.

3.3. Measurement of stability

The clock stability is determined by the quantum projection noise (QPN) in single-ion optical clocks and the Dick noise in optical lattice clocks. The QPN limited stability can be expressed by[30]

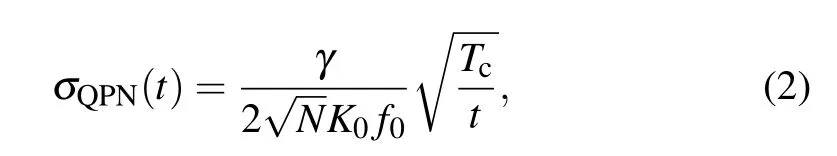
whereγis the linewidth;fis clock transition frequency;K=|dPe/dδ|γis the maximum frequency sensitivity, whereδis the detuning of the clock laser frequency from the resonance,Peindicates the excitation fraction at the detuning ofδ, and for Rabi spectrum, C equals the maximum excitation fraction;N ≈1.2×104is the number of atoms;Tc=950 ms is the clock detection cycle andtis the averaging time.

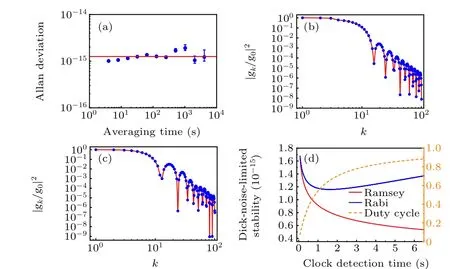
Fig.5. Frequency flicker noise floor of the clock laser and calculation of the normalized Fourier coefficients. (a) Allan deviation of the clock laser frequency corrections after reducing the linear frequency drift. Red solid line is the linear fitting with a fixed slope of zero, which shows that the frequency flicker noise floor of the clock laser is 1.29×10-15.(b)Squared magnitude of the normalized Fourier coefficients for Rabi detection with clock laser pulse duration of 100 ms and Tc=950 ms. (c)Squared magnitude of the normalized Fourier coefficients for Ramsey detection with T =50 ms, τ =25 ms,and Tc =950 ms. (d) Calculation of Dick-noise-limited stability for Rabi and Ramsey interrogation. During calculation, dead time for both detection methods stays constant(0.85 s). Stability of Ramsey detection is more than 1.25 times the Rabi detection as the clock detection time is more than 0.85 s(corresponding to a clock duty cycle of 0.5).

According to Eq.(2),with the same clock detection time of 100 ms,γis 8 Hz for Rabi spectrum and 6.6 Hz for Ramsey spectrum (T=50 ms andτ=25 ms). The QPN limited stability is 7.7×10-17@1 s and 5.7×10-17@1 s for Rabi and Ramsey detection, respectively, indicating that the expected clock stability of Ramsey detection will be superior to that of Rabi detection. However,the Dick noise,originating from the down-converted high-frequency noise of the clock laser due to the periodic interrogation, usually dominates the stability of optical lattice clocks.[36]Using the flicker noise floor of the clock laser to approximate and infer the one-sided power spectral density of the clock laser,the Dick-noise-limited stability can be written as[36]

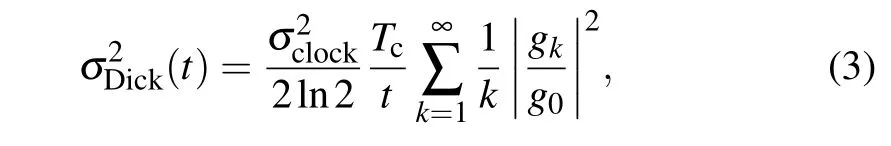
whereσclockis the frequency flicker noise floor of the clock laser and given by analyzing the frequency correction signals(removing the linear frequency drift), as shown in Fig. 5(a)(the measured flicker noise floor is 1.29×10-15);gkis the Fourier coefficients of the frequency-sensitive function.[36]Figures 5(b) and 5(c) demonstrate the squared magnitude of the normalized Fourier coefficients of Rabi and Ramsey detection, respectively. Thus, the Dick-noise-limited stabilities of Rabi and Ramsey detection are 1.59×10-15and 1.53×10-15,respectively,indicating that the influence of the QPN is negligible. Figure 5(d)demonstrates the Dick-noise-limited stability of Rabi and Ramsey detection as a function of clock detection time and indicates that with increasing the clock detection time,the stability of Ramsey detection will be obviously better than Rabi detection.

Fig. 6. Measurements of single clock stability using the interleaved stabilization method. (a) Stability using the 8.5 Hz Rabi spectrum. Inset shows the Rabi spectrum with a clock laser pulse duration of 100 ms. (b)Stability using the 6.3 Hz Ramsey spectrum. Inset demonstrates the Ramsey spectrum with T =50 ms and τ =25 ms. In both (a) and (b), the clock detection cycle is 950 ms(Tc=950 ms). Red solid and black dashed lines represent the calculated Dick-limited stability and QPN-limited stability,respectively.

Under the same parameters, with the previous calculations, the stability of the87Sr optical lattice clock is experimentally measured by Rabi detection and Ramsey detection,respectively. Here, the stability of a single clock is inferred from the single-peak interleaved self-comparison stability by dividing it by a factor of 2.[37-39]The measured stability is 1.71×10-15@1 s for Rabi detection and 1.62×10-15@1 s for Ramsey detection. The experimentally measured stability is slightly lower than the corresponding calculations of Dicknoise-limited stability,which may be caused by the clock not always being able to probe the atomic resonance line at a halfwidth point where the frequency sensitivity is at maximum.Thus,only the theoretical calculation is considered.

4. Conclusion and perspectives

In summary, based on the87Sr optical lattice clock, the optical Ramsey is realized, and the corresponding linewidths agree well with theoretical expectation. The coherence time of 340(23)ms is extracted from the 1/e Gaussian decay of the Ramsey contrast,and is consistent with the dephasing time of 306(11) ms obtained by fitting the damping Rabi oscillation.With the same clock duty cycle, the stability of our clock is experimentally measured, and the results agree with the corresponding theoretical calculations of Dick-noise-limited stability. The clock stability will not be obviously improved by using the narrower Ramsey spectrum,until the clock duty cycle is near or beyond 0.5,or the Dick effect is made lower than the QPN by reducing the clock laser noise,[38]using the zerodead-time clock technique[13]or the quantum non-demolition measurement.[12]It is worth mentioning that Ramsey detection is quite sensitive to phase variation between the clock laser and the atoms,indicating that precise control of the clock laser phase is critical, otherwise, unexpected systematic shift may occur and deteriorate the clock accuracy.

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant No. 61775220), the Key Research Project of Frontier Science of the Chinese Academy of Sciences (Grant No. QYZDB-SSW-JSC004), and the Strategic Priority Research Program of the Chinese Academy of Sciences(Grant No.XDB21030100).