Multifractal analysis of the software evolution in software networks
2022-03-12MeiliLiu刘美丽XiaogangQi齐小刚andHaoPan潘浩
Meili Liu(刘美丽), Xiaogang Qi(齐小刚), and Hao Pan(潘浩)
School of Mathematics and Statistics,Xidian University,Xi’an 0710071,China
Keywords: software,multifractal,box-covering algorithm
1. Introduction
Software systems are gradually increasing in terms of size and complexity due to the rapid development of the Internet, and developers are paying more attention to software engineering and system designs. Software is created to solve practical problems,but problems and requirements are always changing.[1]To this end, software needs to constantly adapt and develop to accommodate changes in the real world. Architecture of software has a profound impact on quality of software, as Torres pointed out in Ref. [2]: the architecture of software system is the foundation for high availability and fault tolerance of software. Software architecture is widely recognized as the backbone for any successful software system.
The widespread use of software systems has attracted researchers to develop a large body of knowledge about software. Software consists of a large number of object classes and the dependencies between them.[3]When software is referred to as a software network (nodes represent classes and edges represent dependencies),[4]techniques in complex networks are available. Chonget al. proposed a method to represent software systems via weighted complex networks and to define the maintainability and reliability of the system regarding the characteristics of the network structure.[5]Yan and Qi showed that large-scale software with complete functions and excellent performance is a scale-free network.[6]The small average shortest path and the connection preference between classes were reflected in this feature.[7]Gaoet al. introduced a measure of software structure and pointed out that there is some degree of exponential decay in both the degree distribution and node weight distribution in software networks.[8]Wanget al. analyzed the relation between the statistical characteristics and influence of nodes in software networks, and proposed the concept of key nodes in software networks.[9]Although software is increasingly adopted by human society,its architecture is not yet completely understood.
Object-oriented technique is advantageous in upgrading software system architecture for its encapsulation,inheritance and polymorphism. Software development based on this technique differs from structure-oriented technique in matter of system architecture, module life cycle and project maintenance. Software requirements are fulfilled by modules with different functions, which makes differences in the dependency between object classes. The complexity of the dependency affects the quality of the software system. Practice in object-oriented software development establishes that the expansion of software scale leads to an increase in the number of object classes. Recently, it has become a hit to build software networks through basic object class dependencies. On this basis,potential features and measurements of software architecture can be explored.[10]
The fractal nature of complex networks is an important structural feature for predicting and interpreting the composition and evolution of networks[11]and was discovered by Songet al.[12]In particular, the dimension in a software network characterizes the degree of cohesion for object classes. Concaset al. found a linear relationship between the dimension and the parameters CBO and RFC in software networks(coupling between object,CBO;response for a class,RFC).[13,14]Turnuet al. investigated the relationship between the dimension and software defects, and adopted it as a global quality metric for software.[15]
The box-covering algorithm was proposed by Mandelbrot and was originally employed to find the fractal dimension of graphs in Euclidean space.[16]It is the most broadly adopted for its simplicity and ease of operation. The method was extended to complex networks by Songet al.,[12]in which the network is covered with boxes of a given “size”. At present,the box fractal dimension algorithms include greedy coloring,compact box burning (CBB) and maximum excluded mass burning (MEMB).[17]The key of the algorithm is to get the minimum number of boxes covering the network,which is NPhard. Scholars have conducted intensive research to advance the algorithm. For instance, a novel edge-covering method was put forward by Zhouet al., which outperformed nodecovering in strictly self-similar networks.[18]On the other hand, the algorithm was modified considering the differences in the node degree distribution,where the number of nodes in the box was calculated by the node degree.[19]
Multifractal is a generalization of fractals in which many fractals are spatially intertwined. Multifractal theory is valuable in many science fields: analysis of natural phenomena such as earthquakes,[20]pattern recognition,[21]air traffic flow,[22,23]vehicle traffic flow,[24]and traffic modeling for computer network.[25]Mishraet al. investigated the localization properties of the adjacency matrix eigenvectors for smallworld networks by this feature.[26]Jianget al. reviewed the methods, models and properties of multifractal analysis in finance, which has implications for other fields as well.[27]In Ref.[28], Zhanget al. performed multifractal analysis in the financial market with small-world topology, which may provide new insights into the problem of the origin of multifractality in financial time series.How multifractal works in varied domains is crucial to understand its practical meaning.
A software system with complex object class dependencies always makes it difficult for engineers to maintain. The dependency distribution in a software network can be described by multifractal. The more irregular the network is,the more obvious the nature of the multifractal becomes. That is, the more complex and chaotic a system is, the stronger its multifractal character behaves. Thus, the multifractal characteristic of software network is strongly linked to software quality. This signifies that a well-designed software system should exhibit weak multifractal characteristic. Investigating whether the software is multifractal can be utilized to improve the performance of existing networks or to design new ones.There are various methods to achieve multifractal analysis in scientific fields, and the box-covering algorithm is one of the classical methods.
In this paper,an improved box-covering algorithm applicable to software network is presented to study the complexity and inhomogeneity of software. Experiments are conducted on different softwares to explore their multifractal nature. In addition,simulation results on different versions of one of the software reveal that the differences in dependencies between object classes decrease as the version evolves.
The contribution of this paper is threefold: (1)We focus on the multifractal property of software network,which is unaddressed by current literature. To the best of our knowledge,previous studies have concentrated on the fractal dimension of software networks. (2) The investigation is oriented to collecting data from software code rather than academic data libraries. (3) The improved box-covering algorithm based on complex networks is applied to software networks,which examines the dependencies between classes in a holistic way.Moreover,the algorithm behaves well in software networks.
The remainder of the paper is organized as follows: Section 2 presents the construction of the software network. In Section 3,we introduce the multifractal analysis method in our work and give a case to illustrate its advantages. Experiments performed in Section 4 verify the multifractal nature of software with different functions. Especially, different versions are analyzed to probe the evolution of the software architecture. Finally,the paper is concluded and the future direction is given in Section 5.
2. Software network
2.1. Software network model
Analyzing the software source code is the first step to obtain structural information. The software at the class level is represented by a weighted directed software network, which takes into account both the coupling strength and direction between classes. For instance, in Fig.1(a), class Letter extends class Paper,and classes People and Pen are members of class Letter. This relation can be portrayed by the class diagram in Fig.1(b).
2.2. Metrics for class dependency
2.2.1. Five dependencies in the unified modeling language
The dependency strengths between object classes are different and need to be weighted. Dependencies between object classes are reflected in software engineering where classes with similar function are placed in the same package or module.In the unified modeling language(UML),the main dependencies include dependence,association,aggregation,composition and generalization.
Dependency means that the accomplishment of the function of one object class requires reference to another object class and that changes in one partially affect the other. Association is a connection,which is stronger than dependency.
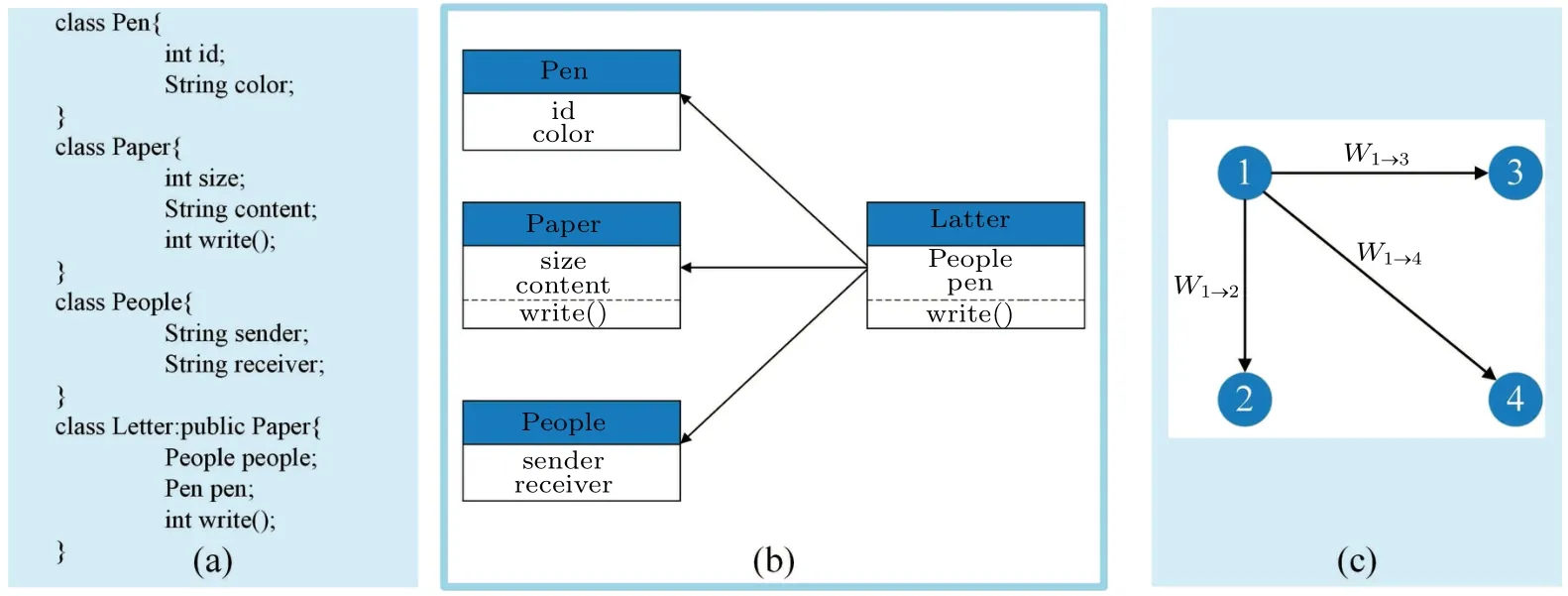
Fig.1. The relations among code,class diagram and software network: (a)code,(b)class diagram,(c)software network.
Two dependent object classes do not add attributes to the object. However,if they are associated,the attributes of one object class are added by the other. Association makes the two object classes more coupled. Aggregate is an association that tends to have one object class containing the other. Composition is a multi-aggregate relationship where an object class contains multiple object classes and depends on them. Generalization indicates the categorical relationship between general and special elements. In practical development, generalization is the inheritance,interface and implementation of object classes. The strength of these five relations is summarized in Table 1,with D1-D5 indicating a progressive strength.
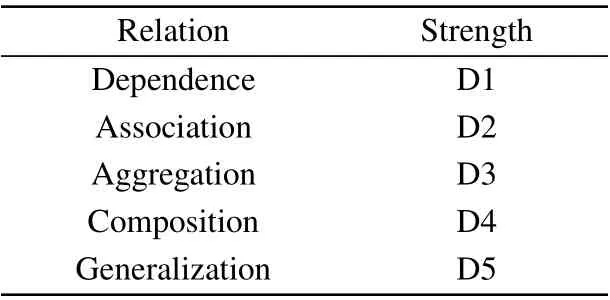
Table 1. The relation between object classes.
2.2.2. CK metrics
Traditional software metrics focus on structured software development paradigm, including functional decomposition and data flow analysis. Since the object-oriented software development paradigm differs significantly from the traditional one, the existing metrics are not suitable. The theoretical research and practice of object-oriented software metrics have become one of the hot topics in the field of software engineering. In this paper, we measure the strength of relations between object classes with improved CK (Chidamber and Kemerer) group metrics, namely, WMC (weighted methods per class) and LCOM (lack of cohesion in methods).[29]The details are given in the following equation:

whereWi→jandLi→jare WMC and LCOM between classesiandj,respectively;α1andβ1are weighting coefficients,satisfyingα1+β1=1.
Considering the above two types of dependency metrics together,a weighted software network is established(see Fig. 1(c)), where the weights of the edges can be determined as

Here,α2andβ2are weighting coefficients, satisfyingα2+β2= 1.Ri→jdenotes the strength of dependency between classesiandjas described in subsection 2.2.1.
3. Method
3.1. Distance
The software network can be mapped to an adjacent matrixW,
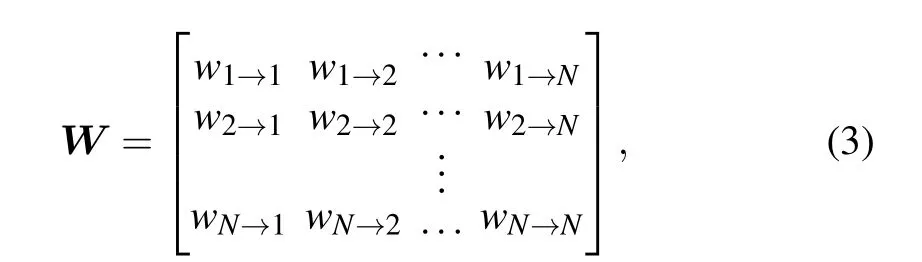
wherewi→jis the edge weight on which object classesiandjdirectly depend. On this basis, the shortest path length between classes(i.e.,the distance between them)is

whereNdenotes the network andN0is its size.Cidenotes the closeness centrality of classi.
3.2. Multifractal analysis
MEMB is the classical box-covering algorithm that tries to find excellent nodes as the box center by the concept of“exclusion mass”. The“excluded mass”of a node is the number of uncovered nodes whose distance from it is less than a given radius. Since the algorithm always selects the center among non-center nodes,including the covered nodes,a node may be covered several times. The choice of the center node has an impact on the effectiveness of the algorithm.
The algorithm in this paper is an improvement of MEMB,which selects the center node by the radio of excluded mass to closeness centrality (REMCC). Assume that the excluded mass of classiisMi. Define the variablefito be

whereτqis the mass exponent of momentq. If the partition function is defined by Eq.(8),the mass exponent is

The mass exponentτ(q) is a strictly monotonic increasing function. It is a concave function that describes whether the research object has distinct multifractal characteristics. If it is linear, the system will be monofractal, otherwise it will be multifractal.[30]The generalized multifractal dimension is extended on this basis and defined as

whereαindicates the velocity at which the mass changes withr, and it determines the singularity strength. The spectrum function is concave, monotonically increasing atq >0 and monotonically decreasing atq <0. It provides a more natural,intuitive and accurate mathematical description for multifractal.
Algorithm 1 gives the concrete practice steps of the REMCC algorithm, which works for the multifractal analysis of software networks. In particular, the excluded mass of the node is counted as the number of classes in the box.Rin line 8 is a value in the range ofr.

Algorithm 1 REMCC algorithm for software networks Require:The set X of all classes and their dependencies.Ensure:Generalized multifractal dimension D(q),multifractal spectrum function f(α).1. Build the directed weighted software network based on class dependencies and Eq.(2);2. for i in X do 3. fi= MiCi;4. end for 5. fp=max i {MiCi};/*Select the class p with maximum fi as the center;*/6. for i in X do 7. dip=min(wPi→p1+wPp1→p2+···+wPpm-1→pm+wPpm→p);/*Calculate the distance between classes i and p*/8. if dip <R then 9.X =X-i/*Update set X */10. end if 11. end for 12. if X!=∅then 13. Return to step 2;14. end if 15. Calculate the distribution of box masses(Eq.(7)).16. Calculate the partition sum(Eq.(8)).17. The mass exponent τ is fitted with partition sum and radius r by least-squares method(Eq.(10)).18. Calculate the generalized dimension D(q)and spectrum function f(α)(Eq.(11)and Eq.(12)).19. Output D(q), f(α).
3.3. Case analysis
An example is given to illustrate that REMCC can achieve fewer boxes compared to MEMB.Given a network,as shown in Fig.2(a),the characteristics of the nodes in the initial state are determined as listed in Table 2.
The detailed process of the two algorithms on this network is shown in Fig. 2. The box size is set to 1. If the center is selected according to the excluded mass (MEMB),node 1 is selected. The first box covers 7 nodes (Fig. 2(b)),and the remaining nodes belong to each of the eight boxes(Fig.2(c)). On the other hand, node 2 is selected if based onfi(REMCC). There are 6 nodes covered by the first box, as shown in Fig. 2(e). In the end, the two algorithms produce distinct box-covering results on the same network. MEMB requires 9 boxes,while REMCC requires only 6 boxes.REMCC has superior results. Specifically,REMCC takes into account the topological characteristics of the network, i.e., the closeness centrality of nodes. Therefore, there will not be a situation where some leaf nodes are isolated by boxes.

Fig.2. Comparison of algorithms.

Table 2. Node characteristics in the initial state.
4. Experiments
4.1. Data extraction
Multifractal analysis is carried out in different Java frameworks:myabtis,dubbo,cxf and fastjson.In detail,mybatis is a persistence framework that supports custom SQL,stored procedures and advanced mappings; dubbo enables applications to realize service input and output through high-performance RPC (Remote Procedure Call); cxf helps you build and develop services using front-end programming APIs; fastjson makes it easy to complete object-to-object and object-to-string conversions. These four frameworks are object-oriented systems,but they have distinctly different functions. Table 3 lists the network topology characteristics, such as the number of nodes and edges.
Additionally, different versions of the myabtis software network are considered and their topology characteristics are given in Table 4. The scale of the network increases with the release, and its topology metrics change accordingly, especially from 3.1.1 to 3.3.0. The increase of clustering coefficient and the decrease of average path length mean that the network progressively exhibits small-world characteristics.

Table 3. Datasets for different software networks.

Table 4. Datasets for different versions of mybatis.
In general, hubs in small-world networks tend to have larger degrees. It is known from the case in Section 3.2 that REMCC has better results for this type of network(larger degree of the center node). In other words,REMCC is effective in software networks.
4.2. Results
Figure 3(a) represents the mass exponent functionsτ(q)of different software networks and they are nonlinear. This proves that these software networks are multifractal as to different dependencies. The prerequisite for evaluating the variation of the generalized multifractal dimensionD(q) withqis to calculate the partition sum (Eq. (8)). In this paper, it is computed fromq=-10.0 toq=10.0 in steps of 0.04,and the results is shown Fig.3(b). The singularity of the object class distribution is correlated with the amplitude ofD(q).It is often used to quantitatively measure the degree of multifractality,so that the wider the spectrum is,the more multifractal it is. Specially,D(q)is a horizontal function in the homogeneous case.It can be seen that fastjson has the strongest singularity in class distribution.

Fig.3. Results of four software networks: (a)the mass exponent τ(q),(b)the generalized multifractal dimension D(q).
Likewise, we can conclude that different versions of the myabtis are multifractal(Fig.4(a))and that the singularity of the dependency distribution is reduced(Fig.4(b)). The singularity is manifested heterogeneity of spatial distribution in the software network. In Figs. 3(b) and 4(b), the left tail of the functionD(q)depicts the low dependency,while the high dependency is associated with the right tail. Classes that are frequently invoked by other modules tend to have a larger degree,while classes with specific functionality that are only used in one module have a small degree. There are significant differences in the spatial distribution of nodes with large degrees.
The maximum,width and asymmetry of the spectrum for different software networks are summarized in Table 5. Generally speaking,the larger the width,the larger the maximum and the better the symmetry, the more pronounced the multifractal characteristic of the network. As before,fastjson has stronger multifractal performance compared to other software.We polyfit the spectrum curve by the least squares method,see Fig. 5, where the red line indicates the binomial curve. The fact that the spectrum function is parabolic implies that the network is multifractal.

Fig. 4. Results of mybatis software networks: (a) the mass exponent τ(q),(b)the generalized multifractal dimension D(q).

Fig.5. Multifractal spectrum curves for different software networks: (a)mybatis,(b)dubbo,(c)cxf,(d)fastjson.
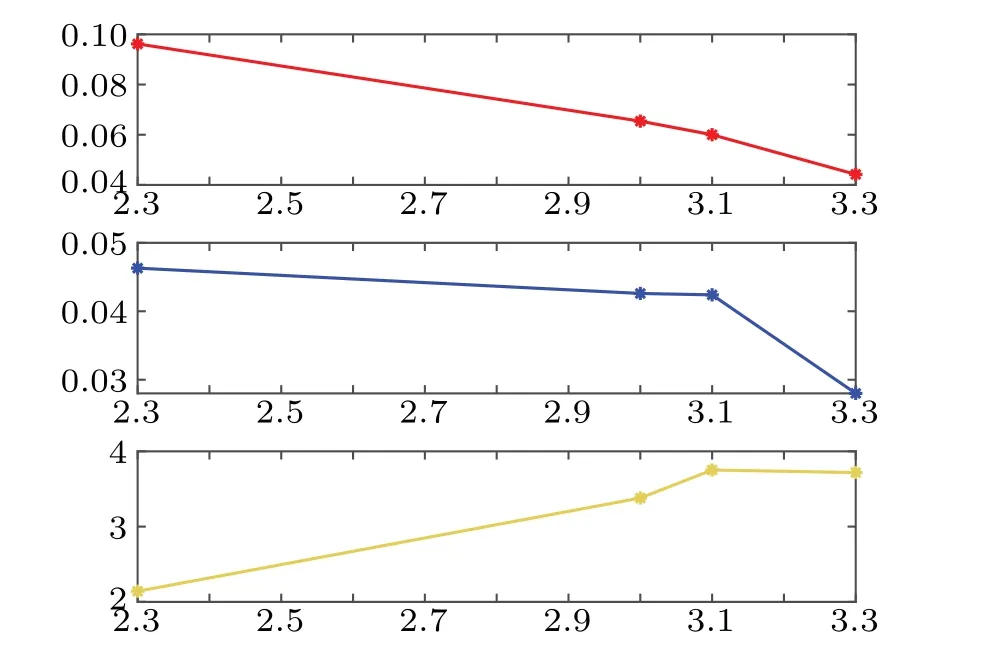
Fig.6. The width(red line),maximum(blue line)and asymmetry(yellow line)of spectrum for different mybatis versions.

Table 5. Multifractal spectrum characteristics for different software networks.
The multifractal spectrum characteristics for different versions of mybatis are shown in Table 6. Narrower spectrum,smaller maximum and increasing asymmetry suggest that the multifractality of mybatis gradually weakens. As a result,the singularity of dependencies between classes is decreased.

Fig.7. Multifractal spectrum curves for different versions of mybatis: (a)mybatis 2.3.5,(b)mybatis 3.0.1,(c)mybatis 3.1.1,(d)mybatis 3.3.0.

Table 6. Multifractal spectrum characteristics for different versions of mybatis.
The results in the table are visualized in Fig. 6. Specifically, the spectrum width is reduced by 44.4% from version 2.3.5 to version 3.3.0. In fact, during the software improvement process, some inapposite dependencies between classes are removed by the new version, thus the singularity in dependencies between classes is gradually reduced. This trend causes a more specific division of functions between software modules.
Figure 7 displays the spectrum function curves for different versions of mybatis,which emphasizes the multifractal nature as well. As we can observe from Figs. 5 and 7, the spectrum curves have a right truncation and a long left tail.Apparently,f(α)increases considerably on the left side of its maximum,while it varies slightly on the right side.
5. Conclusions
In summary, a multifractal analysis approach based on modified box-covering algorithm is introduced to discuss the software structure. We analyze the dependencies of class objects in software at the code level to construct software network. The experiments are performed on four representative software and they are found to be multifractal. Moreover,they have different functions and are applied to different modules of the system. In other words,even functionally different software has similarities in architecture design. Furthermore,simulation on different versions of mybatis demonstrates that the singularity of dependencies between object classes decreases with the optimization of the software. The methodology and results of this paper provide new insights into the evaluation and design of large-scale software systems. Future work will focus on the relationship between software defects or reliability and the multifractal property of software networks.
Acknowledgement
Project supported by the National Natural Science Foundation of China(Grant Nos.61877067 and 61572435).
杂志排行
Chinese Physics B的其它文章
- Measurements of the 107Ag neutron capture cross sections with pulse height weighting technique at the CSNS Back-n facility
- Measuring Loschmidt echo via Floquet engineering in superconducting circuits
- Electronic structure and spin-orbit coupling in ternary transition metal chalcogenides Cu2TlX2(X =Se,Te)
- Characterization of the N-polar GaN film grown on C-plane sapphire and misoriented C-plane sapphire substrates by MOCVD
- Review on typical applications and computational optimizations based on semiclassical methods in strong-field physics
- Quantum partial least squares regression algorithm for multiple correlation problem
