Optical scheme to demonstrate state-independent quantum contextuality

Ya-Ping He(何亚平) Deng-Ke Qu(曲登科) Lei Xiao(肖磊)Kun-Kun Wang(王坤坤) and Xiang Zhan(詹翔)

1Department of Physics,Southeast University,Nanjing 211189,China

2Beijing Computational Science Research Center,Beijing 100084,China

3School of Physics and Materials Science,Anhui University,Hefei 230601,China

4School of Science,Nanjing University of Science and Technology,Nanjing 210094,China

5MIIT Key Laboratory of Semiconductor Microstructure and Quantum Sensing,Nanjing University of Science and Technology,Nanjing 210094,China

Keywords: state-independent quantum contextuality,optical systems

1. Introduction

The debate of whether quantum mechanics(QM)can be explained by hidden variable theory has been discussed for many years.[1]In 1964,Bell’s theorem showed that local hidden variable (LHV) cannot reproduce QM and gave an inequality for experiment.[2]The manifestation of quantum nonlocality requires spacelike separated experiments and entangled states. LHV theories are a special type of noncontextual hidden variable (NCHV) theories, which can determine that the predetermined measurement resultO(X)of an observableXis independent of other compatible measurements being carried out simultaneously. Remarkably, Kochen-Specker (KS)theorem illustrates that NCHV is in conflict with the predictions of QM.[3-5]The test of the KS theorem requires neither spacelike separation nor any special quantum state.

Contextuality is proven either by a logical contradiction between the NCHV predictions and those of QM or by the noncontextual inequalities. So far, the simplest contextual inequality pointed out by Klyachko-Can-Binicioglu-Shumovsky(KCBS)requires a single three-dimensional quantum system[6]and has been tested experimentally.[7]Nevertheless, the inequality is state-dependent, while the proofs of the KS theorem requires neither a composite system nor any quantum special quantum state. State-independent noncontextual inequalities are more robust against noise in initial state preparation than the state-dependent one. Recently, quantum contextuality has been demonstrated in the nitrogen-vacancy center,[8]trapped ions,[9,10]neutron experiments,[11,12]and photonic systems.[13-23]

Here we propose an experiment test of state-independent contextuality proof known as the Mermin pentagram in eight-dimensional Hilbert space.[24,25]The contextuality can be proven by the violation of a KS inequality derived by Cabello.[26]Our scheme can be implemented either in an individual system or in a composite one with optical components and demonstrate that the entanglement might not be necessary for quantum information processing.

2. Theoretical method

As the simplification of the KS theorem, ten binary±1 observables are considered in Mermin’s magic pentagram.They can be written as

whereσxandσyare the Pauli observables, andIis the identity operator. According to the compatible relations, these observables can be simultaneously measured in five groups{Y1,X2,Y3,P2},{X1,Y2,Y3,P1},{X1,X2,X3,P4},{Y1,Y2,X3,P3}and{P1,P2,P3,P4}as shown in Fig.1. In particular, the measured product of the group{P1,P2,P3,P4}has different result in noncontextuality and contextuality theory.In the quantum theory, the measured product of the four observables in each line of the five lines but the horizontal one is+1 so that the measured product of five lines is-1. However,in any noncontextuality theory,the measured product over all observables of five lines must be +1. This is because each observable appears twice at the intersection of two different lines.

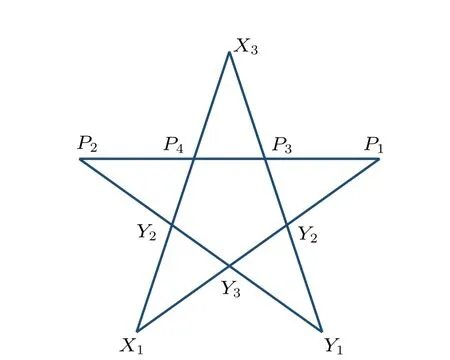
Fig.1. Mermin pentagram. The observables in the same line are mutually compatible and form a group. The product of the results of observables in each of the six lines is+1 except for the horizontal line,where the product is-1.

To demonstrate the property, a noncontextual inequality can be constructed from the ten observables mentioned above because no experiment yields perfect measurement. The noncontextual inequality derived in Ref.[26]reads

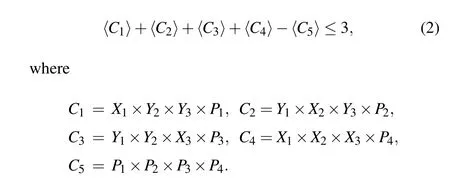
The joint measurements of four compatible observables do not have to be performed simultaneously, and they can be measured in sequence.The scheme of sequential measurement is shown in Fig.2.

Fig.2. M1, M2, M3, M4 correspond to four sequential measurements in a context. Each M has a binary outcome (the value is -1 or 1), a context measurement has 16 kinds of measurement results.

In the above inequality,the classical upper bound is 3,and the quantum upper bound is 5. The state-independent property and a large violation from the classical bound are robust against the experiment noise. Therefore, we can demonstrate the conflict between noncontextuality and quantum mechanics by testing whether the inequality is violated.

3. Experimental schemes

In the following content,we will design an experimental scheme in the individual system and the composite system to verify this state-independent noncontextual inequality.

3.1. Individual system

In the experimental scheme,the herald single photons are yielded via type-I spontaneous parametric down-conversion in aβ-barium-borate(BBO)nonlinear crystal.[27-34]Firstly, the heralded single photons pass through a polarizing beam splitter(PBS)and a half-wave plate(HWP).Then the photons are separated into two paths by a birefringent calcite beam displacer (BD).[35-39]The BD directly transmits the vertically polarized photons into the left path (L) and splits the horizontal photons into the right path (R). Next, two paths pass through two HWPs and a BD. Especially, the BD transmits the vertically polarized photons into the down path (D) and splits the horizontal photons into the up path(U).Finally,we add appropriate HWPs to the four paths to adjust their polarization and yield arbitrary quantum states. The experimental scheme is shown in Fig.3. The eight-dimensional system can be encoded by using the degree of freedom of the photon’s polarization and path. The corresponding bases are

That is,|ULH〉indicates that horizontally polarized photons are on the left side of the up path. After the initial state preparation, we will introduce the experimental implementation of one of the four observables in sequential order.

Especially,the Pauli matrix of an observable can be written asM=∑i=H,V mi|mi〉〈mi|,whereM=(σx,σy,I)and|mi〉is the eigenstate related to corresponding eigenvaluemiofM. Measurement of any other observable can be reduced to detectσzby applying a suitable unitary transformationUM=|H〉〈mH|+|V〉〈mV|,so that the overlap between the initial state and eigenstate|mi〉is tested by measuring the probability ofHandV.

In measurement-1, we measure the polarization information of photons after the initial state preparation by using HWPs and PBS. The angle of these HWPs can be obtained from Ref. [20]. Then, we use HWPs and a BD to merge the left and right path into the right path, so that we can convert left and right path information of this photon into polarization.HWPs after the first BD can realize theUMon the degree of freedom, and the left and right path and the probability ofHandVcan be tested by the second PBS. Similarly, there are HWPs and the second BD to merge the up and down path into the down path. HWPs after the second BD can realize theUMon the degree of freedom of the up and down path and the probability ofHandVcan be tested by the third PBS.

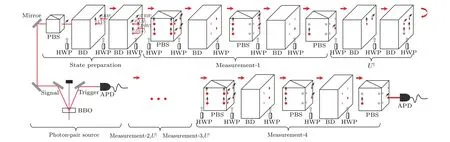
Fig.3. The individual system realizes the contextuality verification of the eight-dimensional Hilbert space. The realization of the eight-level system here uses the polarization and path of the single photon. The four observables are measured in sequential order. The measurements are realized by using the half-wave plates(HWPs)and beam displacer(BD)and the photons are detected by APD.

For the measurement of an observable in eightdimensional system, the outcome is one of the following eight kinds of combinations:{1,1,1},{1,1,-1},

{1,-1,1},{1,-1,-1},{-1,1,1},{-1,1,-1},{-1,-1,1}

and{-1,-1,-1}. The product of three values in each combination is 1 or-1. Before the next measurement is done,the measured states need to be restored to the eigenstate of the Pauli matrix by adding a HWP behind the PBS. The following experimental measurement process is the same as that of measurement-1, but there is no state reconstruction after measurement-4. Finally, for the four observables, there will be 23×23×23×23=4096 kinds of result distribution. In our scheme,it is crucial to mention that the measurement only corresponds to one of the 4096 distributions and the input-output statistics can be obtained by repeating the experiment, with the appropriate HWPs choices, 4096 times and recording the number of photons detected in same time.

3.2. Composite system

In the composite system, using the degree of freedom of polarization of three photons, the basis states of an eightdimensional system can be encoded as

HereHandVare the horizontal and vertical polarization of the photon, respectively. The three positions in the arrangement sequence indicate the polarization of the first, second,and third photons. For instance,|VHV〉indicates that the first photon is vertically polarized, the second is horizontally polarized and the third is vertically polarized.

Fig.4. (a)Conceptual experimental setup for verification of non-contextual inequality. Three-photon GHZ state consists of two spontaneous parametric down-conversion(SPDC)sources. The abbreviations of the components are I-BBO, β-barium-borate crystal cut for collinear type-I phase-matching;C-BBO, two type-II beamlike phase-matching β-barium borate (BBO) crystals with one HWP; HWP, half-wave plate; QWP, quarter-wave plate; IF,interference filter;PBS,polarizing beam splitter;APD,avalanche photodiode detector. M1,M2,M3,and M4 represent four consecutive measurements.The measurements are realized by using the HWPs and PBSs. (b). The circuit diagram for the local measurement. The UM and the measurement represent the realization of each of the 10 observables.U†M after measurement part performs the eigenstate recovery operation.

For the local measurement ofM(M=σx,σy,I)in above observables, we haveM=∑i=H,V mi|mi〉〈mi|, where|mi〉is the eigenstate with its corresponding eigenvaluemiofM. Polarization rotation operationUM=(|H〉〈mH|+|V〉〈mV|) realizes the transformation of the eigenstate ofMto horizontal polarization (H) and vertical polarization (V) projection measurement.[40,41]After that,the projection measurement of|mi〉(i=H,V)is equivalent to project the state to a different polarization state. We can get the probability of each eigenvalue by measuring the probability ofHandV. Then the expected value ofMcan be obtained through the calculation. To perform the next measurement in the context,we need to applyU†Mto restore the output state to the eigenstate of the measurementM.[42,43]The process of general measurement is shown in Fig.4.

In the optical network,[43-53]the first HWP before a PBS can realize theUMin the right-hand side of Fig. 4(a), which converts after the eigenstates toHorV. In addition, we can use a HWP before PBS to select corresponding measurement valueH(1)orV(-1),which is not shown here. The HWP after the PBS can realize hermitian conjugate ofUM,which can bring back the measured state to the eigenstate ofM. M1,M2,M3, and M4 correspond to four sequential measurements in different contextsCk(k=1,2,3,4,5). After the initial state preparation, the encoded three photons enter M1 to achieve the first measurement,and the output is one of the eight possible results. Then the photon goes into M2,M3,and M4 ends up with one of the 4096 kinds of outputs. One can collect the photon number distribution from APDs by repeating the experiment. The probability distributions of the 4096 kinds of types can be obtained by the ratio calculation. We get it by dividing the number of photons in one of the 4096 distributions by the total number of photons. The expected value ofCkis calculated with the measurement result and corresponding probability distributions. The violation of inequality 2 can be obtained by the five expected values.

4. Discussion

4.1. Measurement of equation

For the scheme we designed, it can be used not only to perform the verification of noncontextual inequality, but also to verify the quantum contextuality with equality ∏4k=1Ok.HereOkis the outcome ofPk. Quantum theory has ∏4k=1Ok=-1,while in classical theory ∏4k=1Ok=1. That means whenO1=O2=O3=1 is true, we can getO4=-1 in quantum theory whileO4=1 in classical theory.[8]Based on this difference, we can verify the conflict of quantum and classical through equality. Here we set M1,M2,M3,and M4 as

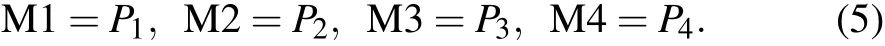
Four successive measurements of M1, M2, M3, and M4 can be realized in the previous section. Using the results of all probability distributions,we can get the value of the equation. The positive or negative of the value can judge whether it conforms to the classical situation or the quantum situation.[8]

4.2. Compatible measurement

A compatibility test is an important relationship in contextuality verification, and our scheme can also be reused for verification. We test it in theA-B-Aform. The measurement ofAandBare compatible if and only if the two outcomes ofAare identical. There are 5×6=30 kinds of compatibility relationships that need to be tested.6 represents the number of compatibility relationships included in a context.

However, this requires us to perform three consecutive measurements to verify the compatible relations. Another method to resolve the compatibility problem is mentioned in Ref.[20],which does not require us to perform additional experiments. Since each observable exists in two different contexts at the same time,we can compare whether the+1 probability of this observable is the identical in different contexts(-1 is also possible).

5. Conclusion

In this paper,we propose a scheme to verify the quantum contextuality in optical systems. We present the methods to test the state-independent inequality and equality[8]to show the differences between quantum contextuality and noncontextuality in the classical world. Arbitrary quantum states are used as the initial states for the state-independent test. We can always obtain the quantum bound of 5 for the left hand of the inequality without any special quantum state. That means the inequality proves the existence of state-independent quantum contextuality. For the equality, we get a result of-1 but 1 in classical,that is,quantum contextuality is verified. Moreover,our scheme is based on a linear optical system,these technologies are currently achievable.[20,54,55]In actual experiments,due to the existence of errors, the quantum state preparation and measurement parts are not perfect. The violation of the inequality can be verified even if the value does not reach the maximum value 5. In the equation verification part,the negative result can show the verification of quantum contextuality.That is to say,our scheme is concrete and feasible.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant No. U1930402). L.X. acknowledges support from the Project Funded by China Postdoctoral Science Foundation (Grant Nos. 2020M680006 and 2021T140045). X.Z.acknowledges support from the National Natural Science Foundation of China (Grant No. 12004184)and the Natural Science Foundation of Jiangsu Province,China(Grants No.BK20190428).

We would like to thank Peng Xue for helpful discussion that greatly improved our manuscript.