Decay properties of the X(3872) through the Fierz rearrangement
2022-03-12HuaXingChen
Hua-Xing Chen
School of Physics, Southeast University, Nanjing 210094, China
Abstract We systematically construct all the tetraquark currents of JPC=1++ with the quark configurationsandTheir relations are derived using the Fierz rearrangement of the Dirac and color indices,through which we study decay properties of the X(3872)under both the compact tetraquark and hadronic molecule interpretations.We conduct a search for the X(3872)→χc0π, ηcππ, and χc1ππ decay processes in particle experiments.
Keywords: exotic hadron, tetraquark state, hadronic molecule, Fierz rearrangement, QCD sum rules
1.Introduction
Since the discovery of the X(3872)in 2003 by Belle[1],many charmonium-like XYZ states have been discovered in the past twenty years [2].They are good candidates of four-quark states consisting of two quarks and two antiquarks, and their experimental and theoretical studies have significantly improved our understanding of the strong interaction at the low energy region.Although there is still a long way to go to fully understand how the strong interaction binds these quarks and antiquarks together with gluons, this subject has become and will continuously be one of the most intriguing research topics in hadron physics [3-10].
The X(3872) is the most puzzling state among all the charmonium-like XYZ states.Although it is denoted as the χc1(3872) in PDG2018 [2], the mass of the charmonium state χc1(2P)was estimated to be 3.95 GeV[11],significantly higher than the X(3872).This challenges the interpretation of the X(3872) as a conventional charmonium state, and various interpretations were proposed to explain it, such as a compact tetraquark state composed of a diquark and an antidiquark[12-17],a loosely-bound hadronic molecular state composed of two charmed mesons [18-24], and a hybrid charmonium state with constituents[25, 26], etc.There were also some studies of the X(3872) as a conventionalstate [27-30], and it was considered as the mixture of astate with acomponent in[31-33].We refer to reviews [3-10] for detailed discussions.
The charged charmonium-like state X(3872) of JPC=1++[34]has been observed in theJ/ψππ,J/ψω,and γJ/ψ decay channels[35-44],and there have been some evidences for the X(3872)→γψ(2S) decay [42, 44].Especially, its decay channels J/ψππ and J/ψω have comparable branching ratios[38-41], implying a large isospin violation.In a recent BESIII experiment [45], evidence for the X(3872)→χc1π decay was reported with a statistical significance of 5.2σ using data at center-of-mass energies between 4.15 and 4.30 GeV, while this was not confirmed in the later Belle experiment[46].We refer to a recent paper [47], where the authors presented a complete analysis of all the existing experimental data and determine the absolute branching fractions of the X(3872) decays.We also refer to another recent paper [48], which studies branching fractions of the X(3872)from a theoretical point of view.There have been many experimental and theoretical studies on this subject, and we refer to reviews [3-10] for more discussions.
In [49] we studied decay properties of the Zc(3900)through the Fierz rearrangement of the Dirac and color indices,and in this paper we shall apply the same method to study decay properties of the X(3872).Both of these two studies are based on our previous finding that the diquark-antidiquark currents ([qq]and the meson-meson currentsare related to each other through the Fierz rearrangement of the Dirac and color indices [50-53].More studies on light baryon operators can be found in [54, 55].The present study follows the idea of the QCD factorization method [56-58],which has been widely and successfully applied to study weak decay properties of (heavy) hadrons.
The X(3872), as either a compact tetraquark state or a hadronic molecular state, contains four quarks.There can be three configurations (q=u/d):

In this paper we shall apply the Fierz rearrangement to relate them,and extract some strong decay properties of the X(3872)under both the compact tetraquark and hadronic molecule interpretations.We shall not calculate the absolute values of these decay widths,but extract their relative branching ratios,which are also useful to understand the nature of the X(3872)[59].A similar arrangement in the nonrelativistic case was used to study strong decay properties of the X(3872) and Zc(3900) in [60-62].
This paper is organized as follows.In section 2 we systematically construct all the tetraquark currents of JPC=1++with the quark contentWe consider three configurations,[cq]and[c][q], and we derive their relations using the Fierz rearrangement of the Dirac and color indices.In section 3 and section 4 we extract some isoscalar decay channels of the X(3872), separately for the compact tetraquark and hadronic molecule interpretations, and in section 5 we investigate its isovector decay channels.The obtained results are discussed in section 6, and formulae of decay amplitudes and decay widths are given in appendix A.
2.Tetraquark currents of JPC=1++ and their relations
Similar to [49], we can use the c,q,quarks (q=u/d) to construct three types of tetraquark currents of JPC=1++, as illustrated in figure 1:

Figure 1.Three types of tetraquark currents.Quarks and antiquarks are shown in red, green, and blue color.

where Γiare Dirac matrices, and the subscripts a, b, c, d are color indices.We separately construct them in the following subsections.
Generally speaking,one can apply the Fierz rearrangement to relate the local diquark-antidiquark currents η(x, x) and the local meson-meson currents ξ(x, x) and θ(x, x), but this equivalence is just between diquark-antidiquark and mesonicmesonic currents,while compact diquark-antidiquark tetraquark states and weakly-bound meson-meson molecular states are totally different.To exactly describe them, one needs to explicitly use non-local currents to perform QCD sum rule analyses,but we are still not able to do this.
2.1.[qc][currents
There are eight independent[q]currents of JPC=1++[63]:





2.4.Fierz rearrangement
The Fierz rearrangement [74] of the Dirac and color indices has been systematically applied to study light baryon and tetraquark operators/currents in[49-55].All the necessary equations can be found in section 3.3.2 of[75].More studies can be found in [69, 76].In the present study we apply it to relate the above three types of tetraquark currents.
The Fierz rearrangement is usually applied to local operators/currents.However, it is actually a matrix identity, and is valid if the same quark field in the initial and final operators is at the same location.As an example, we can apply the Fierz rearrangement to transform the non-local current with the quark fieldsη (x ′, x ; y ′, y) =into a combination of several non-local currents with the quark fields at same locationsθ ( y , x ; y ′ ,x ′ ) =
To apply it to study the decay process, we need to add two overall dynamical processes in the first and third steps:

which will be discussed in detail in the next section.The second step is the Fierz rearrangement whose explicit expressions are given as follows.and:

the following relation betweenand:

the following relation amongand:

Altogether, we obtain the following relation between the currents and the following relation betweeny,x′ ;y′,x) and(y,x;y′ ,x′):

2.5.Isospin of the X(3872) and decay constants
In the present study we shall first use isoscalar tetraquark currents to study decay properties of the X(3872), for example,

Hence,we need couplings of light isoscalar meson operators to light isoscalar meson states,which are summarized in table 1.We also need couplings of charmonium operators to charmonium states as well as those of charmed meson operators to charmed meson states, which are also summarized in table 1.We refer to [49] for detailed discussions.
Since light scalar mesons have a complicated nature [77], couplings of the light scalar-isoscalar meson operatorto f0mesons are quite ambiguous, where f0can be either the f0(500) or f0(1370), etc.In this paper we shall simply use the f0(500) meson to estimate relevant partial decay widths, whose coupling to PSis assumed to be

In the present study we simply average among the decay constantsfχc0andto obtain

The isospin breaking effect of the X(3872) is significant and important to understand its nature.There have been many studies on this,and we refer to reviews[3-10]for detailed discussions.In the present study we shall study this effect by freely choosing the quark content of the X(3872) [12, 65, 66], for example,

where θ andθ′are the two related mixing angles.We shall fine-tune them to be different fromθ= 45° /θ′= 0° in section 5,so that the X(3872) is assumed not to be a purely isoscalar state.To study this, we need couplings of light isovector meson operators to light isovector meson states, which are also summarized in table 1.
3.Decay properties of the X(3872) as a diquark-antidiquark state.


Operators IGJPC Mesons IGJPC Couplings Decay Constants=J qq S ¯ 1-0++ - 1-0++ - -γ=J q iq P ¯ 5 1-0-+ π0 1-0-+ 〈0|JP|π0〉=λπ λ = +π fπ mπ m m u d 2 γ=μ μ J q q V ¯ 1+1- ρ0 1+1- 〈 ρ〉 =μ ρ ρ μ J m f 0 V 0∣ ∣ ∈ fρ=216 MeV[94]γ γ=μ μ J q q A 5¯ 1-1++ π0 1-0-+ 〈 π〉 =μ μ π J p f 0 i A 0∣ ∣ fπ=130.2 MeV[2]a1(1260) 1-1++ 〈 〉 =μ μ J a m f 0 A a a 1 1 1∣ ∣ ∈ f =254 a1 MeV[95]σ=μν μν J q q T ¯ 1+1±--- ρ0 1+1- 〈 ρ〉 = -μν ρ μ ν ν μ J f p p 0 i T T 0∣ ∣ ( )∈ ∈ =ρ f 159 T MeV[94]b1(1235) 1+1+- 〈 〉 =μν μναβ α β J b f p 0 i T bT 1 1∣ ∣ ∈ ∈ f =180 bT 1 MeV [96]=P qq S ¯ 0+0++ f0(500) (?) 0+0++ 〈P f〉 =m f 0 S f f 0 0 0∣ ∣ f ~380 f0 MeV(?)γ=P q iq P ¯5 0+0-+ η 0+0-+ - -γ=μ μ P q q V ¯ 0-1- ω 0-1- 〈 ω〉 =μ ω ω μ P m f 0 V∣ ∣ ∈ fω ≈fρ=216 MeV[94]γ γ=μ μ P q q A 5¯ 0+1++ η 0+0-+ 〈 η〉 =μ μ η P p f 0 i A∣ ∣ fη=97 MeV[97, 98]f1(1285) 0+1++ - -σ=μν μν P q q T ¯ 0-1±--- ω 0-1- 〈 ω〉 = -μν ω μ ν ν μ P f p p 0 i T T∣ ∣ ( )∈ ∈ ≈=ω ρ f f 159 T T MeV[94]h1(1170) 0-1+- 〈 〉 =μν μναβ α β P h f p 0 i T hT 1 1∣ ∣ ∈ ∈ ≈ =f f 180 hT bT 1 1 MeV[96]=I cc S ¯ 0+0++ χc0(1P) 0+0++ 〈 χ 〉 = χ χ I m f 0 S c0 c0 c0∣ ∣ =χf 343 c0 MeV[99]γ=I c ic P ¯5 0+0-+ ηc 0+0-+ η λ〈 〉 = η I 0 Pc c∣ ∣λ =η fη mη m2 c 2 c c c γ=μ μ I c c V ¯ 0-1- J/ψ 0-1-ψ〈 〉 =μ ψ ψ μ I J m f 0 V J J∣ ∣ ∈ fJ/ψ=418 MeV[100]γ γ=μ μ I c c A 5¯ 0+1++ ηc 0+0-+ 〈 η〉 =μ μ η I p f 0 i A c c∣ ∣ =ηf 387 c MeV[100]χc1(1P) 0+1++ 〈 χ 〉 =μ χ χ μ I m f 0 A c1 c1 c1∣ ∣ ∈ =χf 335 c1 MeV[101]σ=μν μν I c c T ¯ 0-1±--- J/ψ 0-1-ψ〈 〉 = -μν ψ μ ν ν μ 0I J f p p i T JT∣ ∣ ( )∈ ∈=ψ f 410 JT MeV[100]hc(1P) 0-1+- 〈 〉 =μν μναβ α β I h f p 0 i T c hT c∣ ∣ ∈ ∈ f =235 hT c MeV[100]=O qc S ¯ 0+ *D0 0+ * * *〈 〉 =O D m f 0 S DD 0 0 0∣ ∣ f* =410 D0 MeV[102]γ=O q ic P ¯5 0- D 0- 〈0|OP|D〉=λD λ = +f m m m D D D c d 2 γ=μ μ O c q V ¯ 1- *D¯ 1- * * *〈 〉 =μ μ O D m f 0 V D D∣ ∣¯ ∈ f* =253 D MeV[103]=μ μ O c q A 5¯γ γ 1+ D¯ 0- 〈 〉 =μ μ O D p f 0 i A D∣ ∣¯ fD=211.9 MeV[2]D1 1+ 〈 〉 =μ μ O D m f 0 A D D 1 1 1∣ ∣ ∈ f =356 D1 MeV[102]σ=μν μν O q c T ¯ 1± D¯* 1- * *〈 〉 = -μν μ ν ν μ O D f p p i T DT 0∣ ∣ ( )∈ ∈ f* ≈220 DT MeV[49]- 1+ - -Timages/BZ_67_890_2898_927_2940.pngaΓ b q l e=1(.u¯CΓ o uu p-l i nd¯g Γsd o)f m 2 e s,oann do pael l r atthoer sl itgoh tm i e so so sc na lsat a r tme se.sAon ll o th p ee rlaitgohrts iPs(oSμ vνPe) c Vto r A mT ehsaovne otpheer aqtuoarrsk J c(Sμ o νnP)te Vn tA q ¯T Γ q h a=v e(u t¯h Γ e u q+u a d r¯k Γ cdo)nten 2 t.Color indices are omitted for simplicity.

As depicted in figure 2, when the q andquarks meet each other and the c andquarks meet each other at the same time,a compact tetraquark state decays into one charmonium meson and one light meson:

Figure 2.The decay of a compact tetraquark state into one charmonium meson and one light meson,which can happen through either(b)a direct fall-apart process, or (c) a process with gluons exchanged.

The first process is a dynamical process, and the second process can be described through the transformation(10):

where we have used
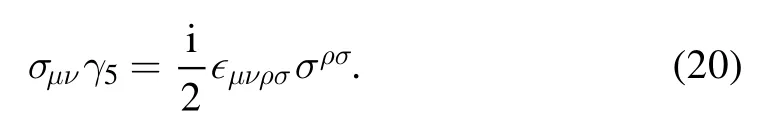
In the above expression we keep only the direct fall-apart process described bybut neglect theO(αs)corrections described by
Together with table 1, we extract the following decay channels:


This decay is kinematically forbidden.
Summarizing the above results, we obtain numerically

from which we further obtain

Detailed calculations can be found in appendix A.
As depicted in figure 3, when the c andquarks meet each other and the q andquarks meet each other at the same time,a compact tetraquark state decays into two charmed mesons.This process can be described by the transformation(11):

Figure 3.The decay of a compact tetraquark state into two charmed mesons,which can happen through either(b)a direct fall-apart process,or (c) a process with gluons exchanged.


Numerically, we obtain

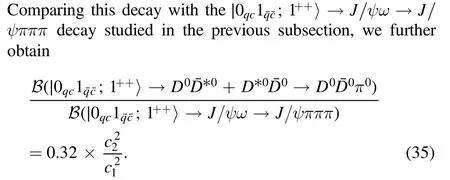
Detailed calculations can also be found in appendix A.As proposed in[61],when the X(3872)decays,a constituent of the diquark must tunnel through the barrier of the diquark-antidiquark potential.However,this tunnelling for heavy quarks is exponentially suppressed compared to that for light quarks,so the compact tetraquark couplings are expected to favour the open charm modes with respect to charmonium ones.Accordingly, c2may be significantly larger than c1, so thatmay mainly decay into theD0D0π0final state.
If the above two processes investigated in section 3.1 and section 3.2 happen at the same time,i.e.,decays into one charmonium meson and one light meson as well as two charmed mesons simultaneously, we can use the transformation(12), which contains the color-singlet-colorsinglet currentsandtogether:

In the above expression we keep all terms, and there is no…any more.Comparing this equation with equations(19)and(30), we obtain the same relative branching ratios as section 3.1 and section 3.2,just with the overall factors c1and c2replaced by others.
4.Decay properties of the X(3872) as a hadronic molecular state

As depicted in figure 4, when the q andquarks meet each other and the c andquarks meet each other at the same time,a hadronic molecular state decays into one charmonium meson and one light meson.This process can be described by the transformation(13):

Figure 4.The decay of a hadronic molecular state into one charmonium meson and one light meson,which can happen through either(b)a direct fall-apart process, or (c) a process with gluons exchanged.
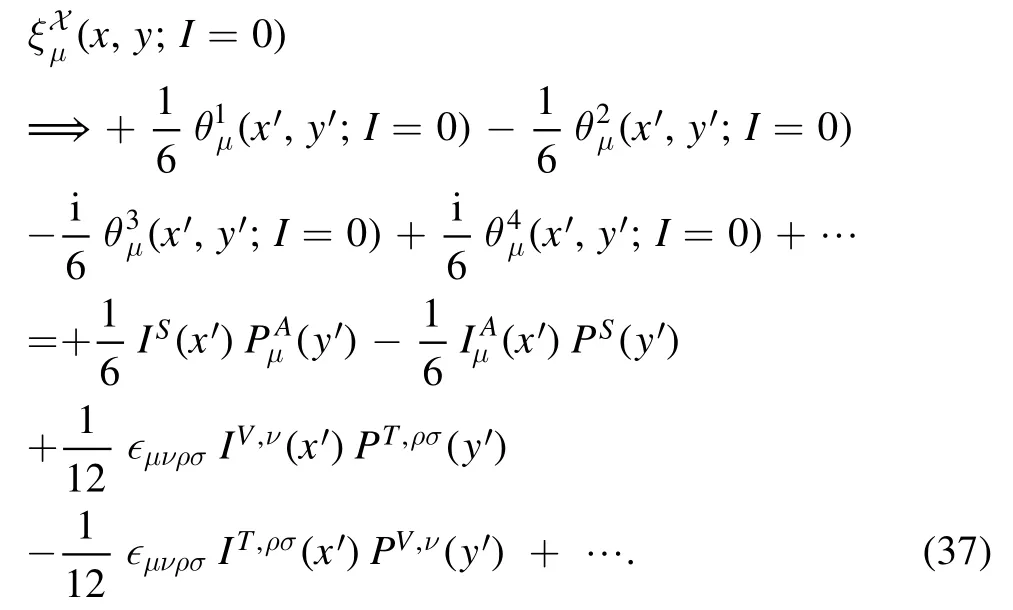
Here we keep only the direct fall-apart process described by,but neglect theO(αs)corrections described by
We repeat the same procedures as those done in section 3.1,and extract the following coupling constants from this transformation:


which ratios are the same as equations (29), obtained in section 3.1 for the compact tetraquark state
Assuming the X(3872) to be thehadronic molecular state of JPC=1++, it can naturally decay into thefinal state, which fall-apart process can be described by itself:

and so
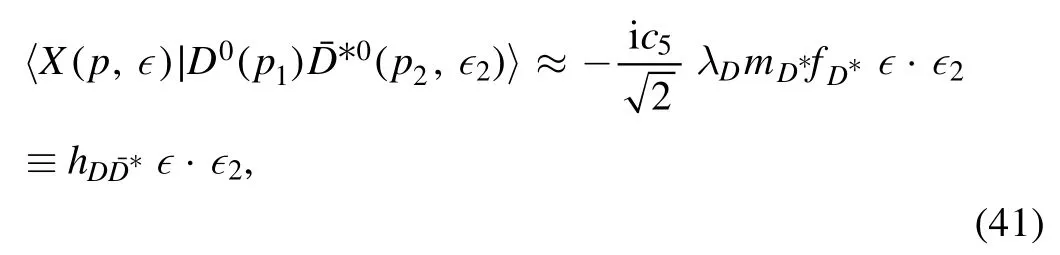

Numerically, we obtain


5.Isospin of the X(3872)
The isospin breaking effect of the X(3872) is significant and important to understand its nature [3-10].As proposed in[78], this can be simply because the close proximity of the mass of the isoscalar X(3872)to the neutralD0threshold.We argue that in this case the X(3872) and theD0threshold together can be considered as a ‘mixed’ state, not purely isoscalar any more, through which we can investigate the isovector decay channels of the X(3872).
In this section we shall investigate the isospin breaking effect of the X(3872) by freely choosing its quark content[12, 65, 66], for example,
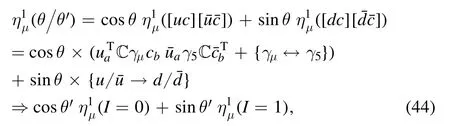
where θ andθ′ are the two related mixing angles.We shall fine-tune them to be different fromθ= 45°/θ′= 0° , so that the X(3872)is assumed not to be a purely isoscalar state.We shall study this effect separately for the compact tetraquark and hadronic molecule scenarios in the following subsections.
5.1.Isospin breaking effect of

Numerically, we obtain

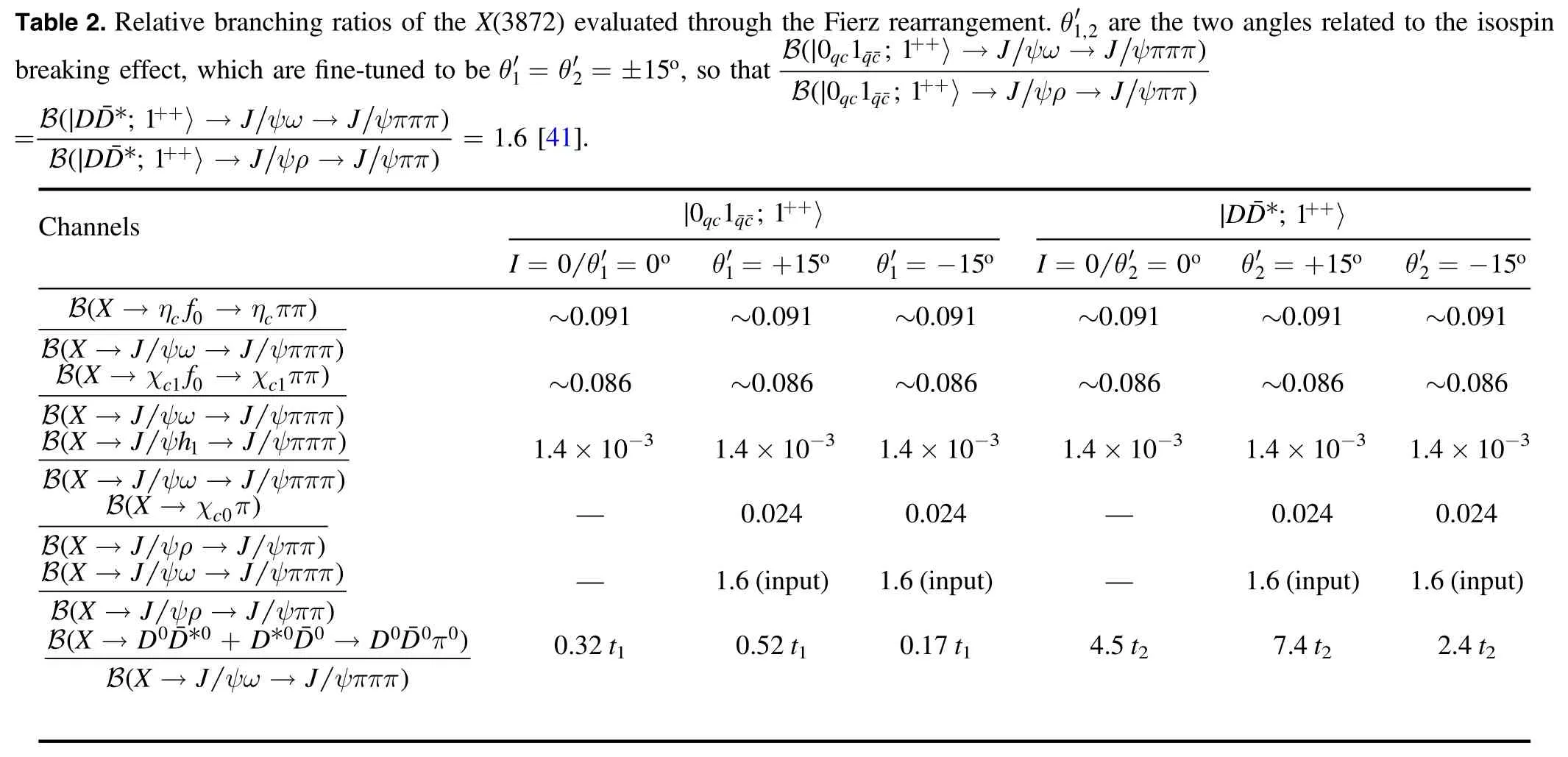
Channels ++〉0 1 ; 1 qc qc∣ ¯¯ * ++〉∣D D¯ ; 1 θ= ′ =I 0 0 1 o θ′ = +15 1 o θ′ = -15 1 o θ= ′ =I 0 0 2 o θ′ = +15 2 o θ′ = -15 2 o η η ππ ψω ψπππ)→ →→ →X f X J J c c 0)B(B(~0.091 ~0.091 ~0.091 ~0.091 ~0.091 ~0.091 χ χ ππ ψω ψπππ)→ →→ →(X f X J J c c1 0 1)B B(~0.086 ~0.086 ~0.086 ~0.086 ~0.086 ~0.086 ψ ψπππ ψω ψπππ)→ →→ →(X J h J X J J 1)B B(1.4×10-3 1.4×10-3 1.4×10-3 1.4×10-3 1.4×10-3 1.4×10-3→χ π ψρ ψππ)→ →X J J c0( )(BX B-0.024 0.024 - 0.024 0.024 ψω ψπππ ψρ ψππ)→ →→ →(X J J X J J)B B(-1.6(input) 1.6(input) - 1.6(input) 1.6(input)* * π ψω ψπππ→+→→ →X D D D D D D X J J 0 0 0 0 0 0 0 B( ¯ ¯ ¯)()B 0.32 t1 0.52 t1 0.17 t1 4.5 t2 7.4 t2 2.4 t2 Table 2.Relative branching ratios of the X(3872) evaluated through the Fierz rearrangement.θ′1,2 are the two angles related to the isospin breaking effect, which are fine-tuned to beθ′ =θ ′ = ±15 1 2 o, so that ψω ψπππ ψρ ψππ〉 → →〉 → →++++J J J J 0 1 ; 1 0 1 ; 1 qc qc qc qc(∣ )(∣ )¯¯¯¯BB**ψω ψπππ ψρ ψππ=〉 → →〉 → → =++++DD J J DD J J; 1; 1 1.6 B(∣ ¯ )(∣ ¯ )B[41].
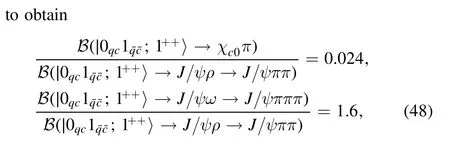
where the latter ratio has been fine-tuned to be the same as the recent BESIII experiment [41].

5.2.Isospin breaking effect of ∣;1++〉


6.Summary and discussions


We first use isoscalar tetraquark currents to study decay properties of the X(3872)as a purely isoscalar state,and then use isovector tetraquark currents to investigate its isospin breaking effect.The extracted relative branching ratios are summarized in table 2, where we have investigated the following interpretations of the X(3872):

In the above expressions, we define the ratioto be the parameter measuring which process happens more easily,the process depicted in figure 2(b)or the process depicted in figure 3(b).Because the exchange of one light quark with another light quark seems to be easier than the exchange of one light quark with another heavy quark[61,79],it can be the case that t1≥1.As discussed in section 4.2, c5is probably larger than c4, so that the other ratio
The above relative branching ratios extracted in the present study turn out to be very much different.This might be one of the reasons why many multiquark states were observed only in a few decay channels[49].We note that in this paper we only consider the leading-order fall-apart decays described by color-singlet-color-singlet meson-meson currents, but neglect the O (αs)corrections described by color-octet-color-octet meson-meson currents, so there can be other possible decay channels,such as X(3872)→χc1π [45].Besides, there is still one parameter not considered in above analyses, that is the phase angle between S- and D-wave coupling constants.We shall investigate its relevant uncertainty in B.
Based on table 2,we conclude this paper.Generally speaking,compared to the Zc(3900)studied in[49],the results of this paper suggest that decay channels of the X(3872) are quite limited:
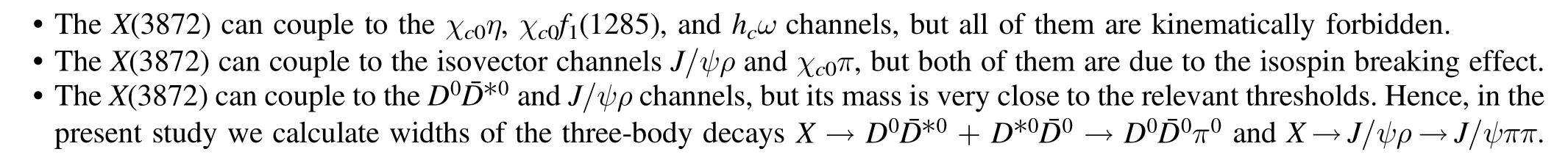
· The X(3872) can couple to the J/ψω and J/ψh1(1170)channels, but both of them are kinematically forbidden.Hence, in the present study we calculate widths of the four-body decays X →J/ψω →J/ψπππ and X →J/ψh1→J/ψπππ.
· The decay processes X →ηcf0→ηcππ and X →χc1f0→χc1ππ might be possible.In this paper we simply use the f0(500) to estimate widths of these two processes, but note that the obtained results do significantly depend on the nature of light scalar mesons,which are still quite ambiguous [77].
To end this paper, we give several comments and proposals:
· The hadronic molecular state ∣D1++〉mainly decays into two charmed mesons, because c5is probably larger than c4.The compact tetraquark statemay also mainly decay into two charmed mesons after taking into account the barrier of the diquark-antidiquark potential (see detailed discussions in [61] proposing c2≫c1).· The isospin breaking effect of the X(3872) is significant and important to understand its nature [3-10].The isovector decay channel X(3872)→J/ψρ →J/ψππ has been well observed in experiments, and recently measured by the BESIII experiment [41] to be:

In the present study we can well reproduce this value under both the compact tetraquark and hadronic molecule interpretations.
Besides this, our result suggests that there can be another isovector decay channel X(3872)→χc0π.Under both the compact tetraquark and hadronic molecule interpretations, we obtain

We refer to [80-87] for more theoretical studies, and propose to study the X(3872)→χc0π decay in the BESIII,Belle-II, and LHCb experiments to better understand the isospin breaking effect of the X(3872).
· Our result suggests that the decay processes X(3872)→ηcf0→ηcππ and X(3872)→χc1f0→χc1ππ might be possible.We note that light scalar mesons have a complicated nature,so our results on these processes are just roughly estimations.
We notice that the BaBar experiment [88] did not observe the γγ →X(3872)→ηcππ process, but that experiment was performed after assuming X(3872) to be a spin-2 state.Moreover,there seems to be a dip structure just at the mass of the X(3872)in the ηcππ invariant mass spectrum, as shown in figure 6(f) of[88].We also notice that the Belle experiment [89] did not observe the X(3872)→χc1ππ decay.They extracted the following upper limit

at 90%C.L.Together with another Belle experiment[90]measuring
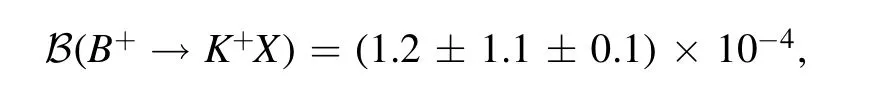
one may roughly estimate

which value seems not small enough to rule out the X(3872)→χc1ππ decay channel.
Again, we refer to [80-87, 91] for more discussions,and propose to reanalysis the X(3872)→ηcf0→ηcππ and X(3872)→χc1f0→χc1ππ processes in the BESIII,Belle-II, and LHCb experiments to search for more decay channels of the X(3872).
Acknowledgments
This project is supported by the National Natural Science Foundation of China under Grant No.11722540 and No.12075019, the Jiangsu Provincial Double-Innovation Program under Grant No.JSSCRC2021488, and the Fundamental Research Funds for the Central Universities.
Appendix A.Formulae of decay amplitudes and decay widths
In this appendix we give formulae of decay amplitudes and decay widths used in the present study.Specifically,the mass of the X(3872) is taken from PDG [2] to be

A.1.Two-body decay X →χc0π0
The decay amplitude of the two-body decay X(3872)→χc0π0is

This amplitude can be used to evaluate its decay width:

where we have used the following formula for the vector meson
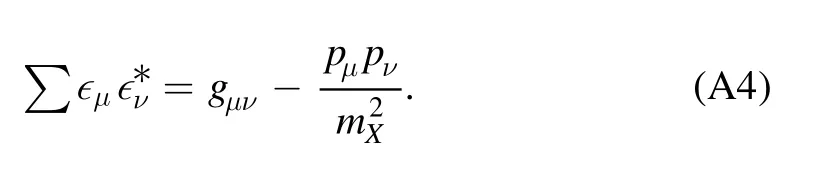
A.2.Three-body decay X →J/ψρ0→J/ψπ+π-
First we need to investigate the two-body decay ρ0→π+π-,whose amplitude is

so that

We can use the experimental parameters=147.8 MeV andB(ρ0→π+π-) ≈100%[2] to extract

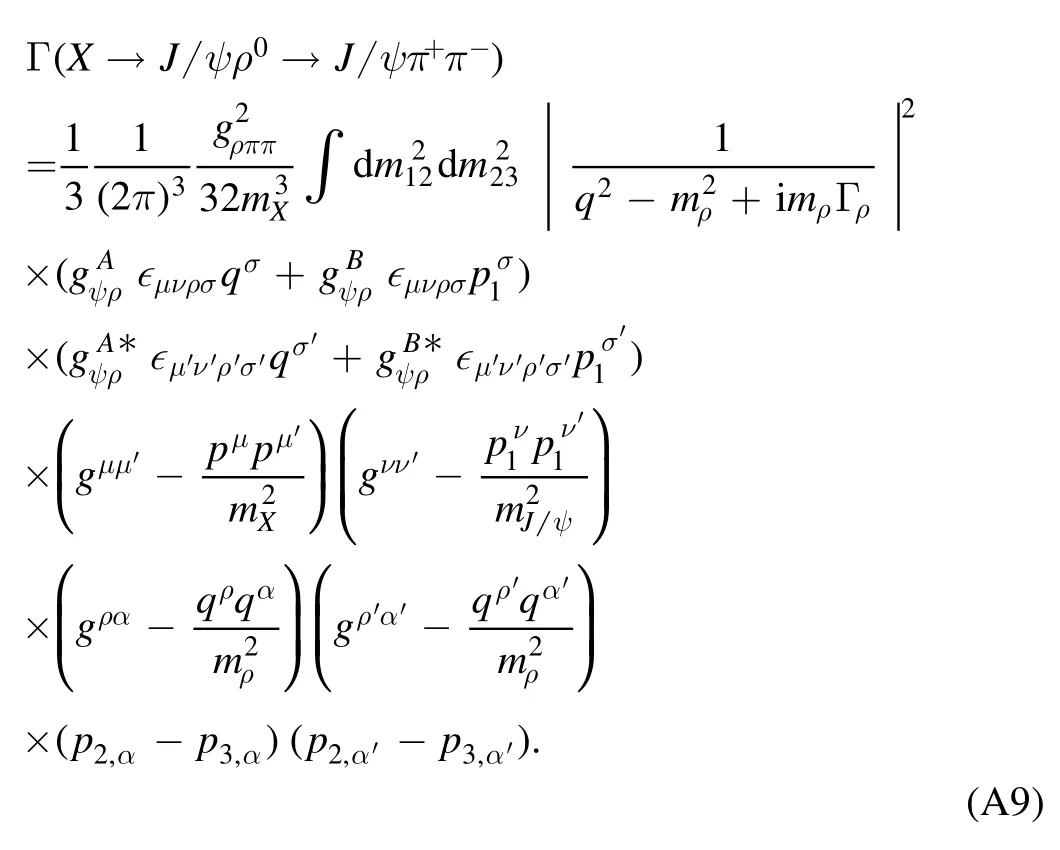
The decay amplitude of the three-body decay X(3872)→J/ψρ0→J/ψπ+π-is

This amplitude can be used to evaluate its decay width:
A.3.Three-body decay X →ηcf0→ηcππ
First we need to investigate the two-body decay f0(500)→ππ, whose amplitude is

In this case we do not differentiate π±,0.The above amplitude can be used to evaluate its decay width:

We can use the experimental parametersmf0=512 MeV and Γf0= 376 MeV [92] to extract

The decay amplitude of the three-body decay X(3872)→ηcf0→ηcππ is

This amplitude can be used to evaluate its decay width:

The X(3872)→χc1f0→χc1ππ decay can be similarly studied.
First we need to investigate the two-body decay D*0→D0π0,whose amplitude is

so that

This amplitude can be used to evaluate its decay width:
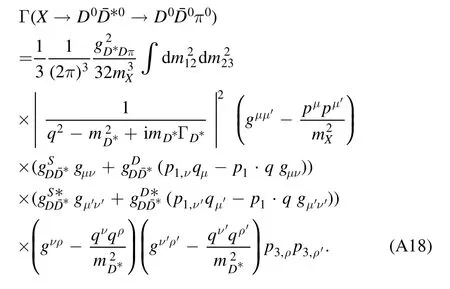

A.5.Four-body decay X →J/ψω →J/ψπ+π-π0
First we need to investigate the three-body decay ω →π+π-π0, whose amplitude is
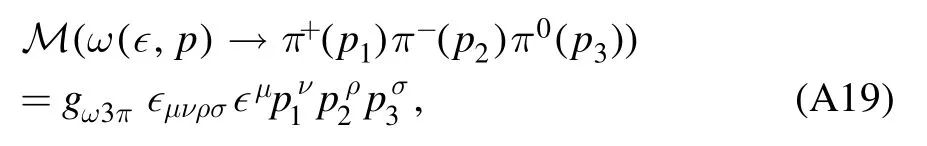
so that
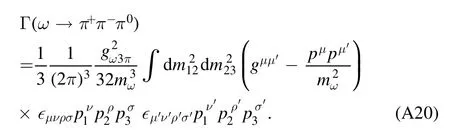
We can use the experimental parameters Γω=8.49 MeV and B(ω→π+π-π0)=89.3%[2] to extract

The decay amplitude of the four-body decay X(3872)→J/ψω →J/ψπ+π-π0is

This amplitude can be used to evaluate its decay width:

The phase space integration is done in the reference frame wherep3=(E3,p3x, 0, 0),and p3xsatisfies p3x>0 as well as
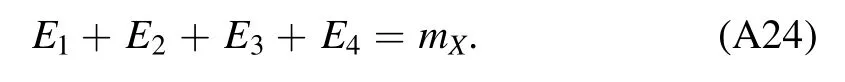
A.6.Four-body decay X →J/ψh1→J/ψπ+π-π0
First we need to investigate the three-body decay h1(1170)→ρπ →π+π-π0, whose amplitude is simply assumed to be

so that
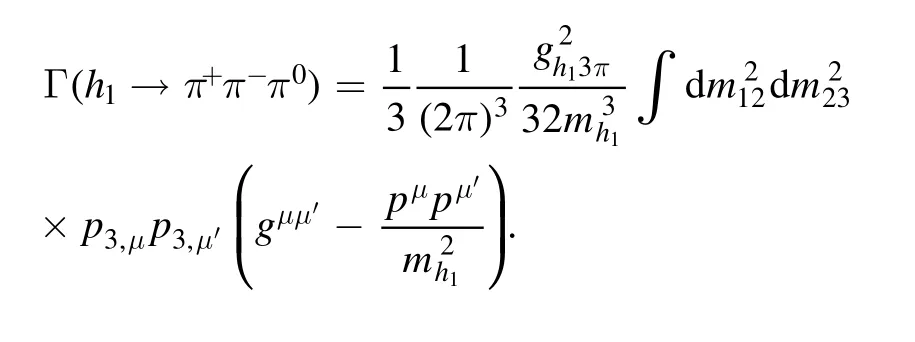
We can use the experimental parametersΓh1= 360 MeV [2]to estimate

The decay amplitude of the four-body decay X(3872)→J/ψh1→J/ψπ+π-π0is

Table 3.Relative branching ratios of the X(3872)evaluated through the Fierz rearrangement.In this table we fix the phase angle θ between the S- and D-wave coupling constantsand to be θ=π.

Table 3.Relative branching ratios of the X(3872)evaluated through the Fierz rearrangement.In this table we fix the phase angle θ between the S- and D-wave coupling constantsand to be θ=π.
Channels ++〉0 1 ; 1 qc qc∣ ¯¯ * ++〉∣D D¯ ; 1 θ= ′ =I 0 0 1 o θ′ = +15 1 o θ′ = -15 1 o θ= ′ =I 0 0 2 o θ′ = +15 2 o θ′ = -15 2 o η η ππ ψω ψπππ)→ →→ →X f X J J c c 0)B(B(~0.091 ~0.091 ~0.091 ~0.091 ~0.091 ~0.091 χ χ ππ ψω ψπππ)→ →→ →(X f X J J c c1 0 1)B B(~0.086 ~0.086 ~0.086 ~0.086 ~0.086 ~0.086 ψ ψπππ ψω ψπππ)→ →→ →(X J h J X J J 1)B B(1.4×10-3 1.4×10-3 1.4×10-3 1.4×10-3 1.4×10-3 1.4×10-3→χ π ψρ ψππ)→ →X J J c0( )(BX B-0.024 0.024 - 0.024 0.024 ψω ψπππ ψρ ψππ)→ →→ →(X J J X J J)B B(-1.6(input) 1.6(input) - 1.6(input) 1.6(input)* * π ψω ψπππ→+→→ →X D D D D D D X J J 0 0 0 0 0 0 0 B( ¯ ¯ ¯)()B 0.021 t1 0.034 t1 0.011 t1 4.5 t2 7.4 t2 2.4 t2
This amplitude can be used to evaluate its decay width:

Again, the phase space integration is done in the reference frame wherep3=(E3,p3x, 0, 0), and p3xsatisfies p3x>0 as well as
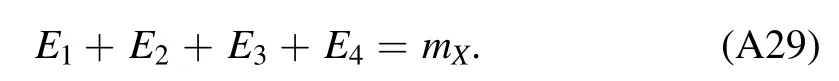
Appendix B.Uncertainties due to the phase angle
There are two different effective Lagrangians for the X(3872)decay into thefinal state,as given in equations(32)and(33):



Using the mixing angle= +15o, we obtain while using the mixing angle= -15o, we obtain

杂志排行
Communications in Theoretical Physics的其它文章
- Influence of an indefinite causal order on an Otto heat engine
- Collapse arrest in a two-dimensional Airy Gaussian beam and Airy Gaussian vortex beam in nonlocal nonlinear media
- Comparison of thermodynamic behaviors of two regular-AdS black holes
- Quantum gravity effects on spectroscopy of Kerr-Newman black hole in gravity’s rainbow
- Shape coexistence in 76Se within the neutron-proton interacting boson model
- Radiative capture of proton by 9Be(p, γ)10B at low energy
