新型水文水井管结构设计与优化研究

徐 俊， 张少锋， 汪发文

(湖北省城市地质工程院，湖北 武汉 430050)

水文水井施工过程中，围填滤料是一道重要的工序，滤料围填质量的好坏，对水文水井的水质和使用寿命具有重要影响。因此，研究滤料围填一直是水井领域的热点问题。除常规的传统填砾方法外，不少专家学者提出了各种不同种类的一体化贴砾滤水管，但是都存在着不少问题，如贴砾层易脱落、滤水管抗压抗折强度变低、生产过程中使用的特殊材料影响污染水质等等。基于这些问题，本文介绍一种新型填砾工艺“管内投砾法”的核心元器件：一种新型井管投砾结构，其结构如图1所示。

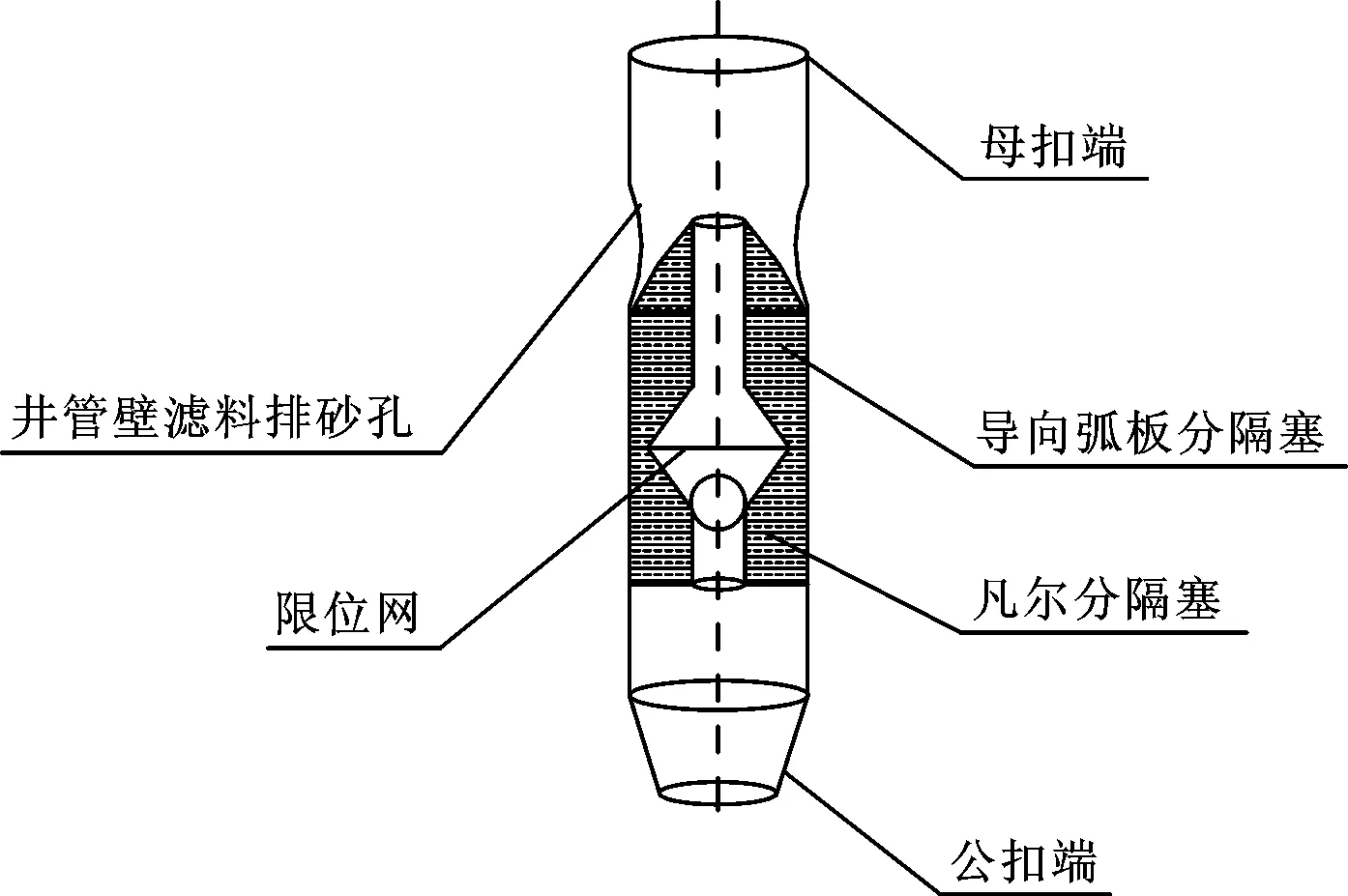
图1 水文水井管内投砾专用接头管总成图Fig.1 Assembly diagram of special joint pipe forinternal gravel in hydrologic well

水文水井管内投砾专用接头管总成由带排砂孔的井管、带导向弧板分隔塞、带凡尔分隔塞三部分组成。带导向弧板分隔塞与带凡尔分隔塞组合安装入由带排砂孔的井管内，弧板底部略低于井管最下部排砂孔[1]。

该结构中，排砂孔的开孔直径影响着井管强度和排砾速度，导向弧板分隔器的角度影响着排砾速度，如何匹配这三个参数，是该结构设计的关键因素。为此，本文以127 mm外径的井管为例，结合仿真与优化，求解该核心元件的最佳开孔直径及导向弧板的斜坡角度，最终在保证井管强度的条件下，快速将滤料从管内投入至目的层位和小间隙二次注浆止水固井[2]，从而解决传统成井工艺中的部分难题。

1 新型投砾方案

1.1 传统投砾工艺

传统的投砾工艺方法包含四种[3]：静水填砾法、注水填砾法、抽水填砾法、多层滤料充填法。以上常用方法只适用于浅井和井壁稳定的中深井。在复杂地层井段的填砾过程中，极易因注水和抽水填砾而导致井壁坍塌或者缩径而无法围填滤料，造成填砾失败。

传统的填砾方法都是管外投砾法，其填砾质量受管外环状间隙、井壁稳定性、井深等多重因素影响，其充填滤料密实度难以保障，直接影响水井供水质量。

1.2 新型投砾方案

新方案[4]的核心元件是管内投砾专用接头。样品由湖北省地质局第三地质大队机械厂定做。其主要由以下几部分组成：带大注浆孔与出砾孔井管；井管上、下部缠绕1 m膨胀橡胶，膨胀橡胶距离大注浆孔0.5 m以上；将导向弧板分隔器与凡尔分隔器固定于井管中；导向弧板分隔器的导向弧板与出砾孔重叠。示意图如图2所示。

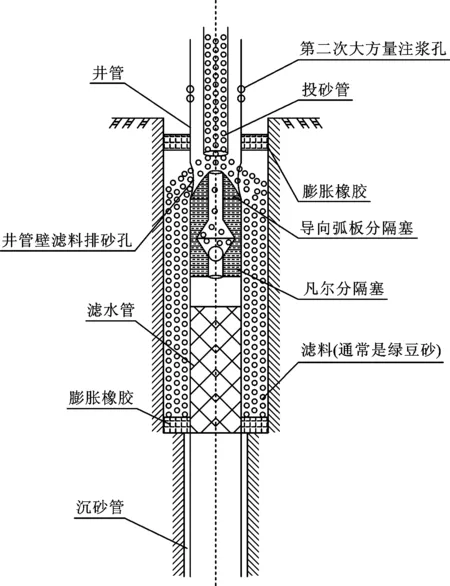
图2 井管投砾示意图Fig.2 Schematic diagram of well pipe gravel throwing

技术核心特征是管内投砾器皿安装后，按照设计下井管、下管内投砾器、投砾、一次小泵量注浆、二次大泵量注浆、扫塞、洗井等作业流程施工。这样无论井的深度多少，都能大幅度降低滤料在环状间隙的填砾运移距离，能简单快捷可靠地投送滤料到目的层位，最终达到填砾与止水固井一体化操作，施工成本低廉。

新型的投砾工艺施工方法包含以下步骤：

(1) 下管。钻孔完工之后，依据地层实际情况，选取目标含水层，按照设计依次下入井管，即沉砂管+滤水管+带管内投砾专业接头+井管(含大注浆孔井管)。

(2) 管内填砾。首先筛选滤料，根据含水层砂粒直径选取其级配直径；然后根据目标含水层长度和深度，计算并备好砾料，再通过投砾管，将砾料连续投至转换接头处，泵入清水，充分密实砾料。

(3) 注浆止水。注浆的目的是封闭填砾孔、大注浆孔以及非取水段的环空间隙。小注浆在填砾结束之后进行，根据环空间隙计算注浆量，并保证管内外水泥柱液面低于大注浆孔。

(4) 扫塞。待水泥浆凝固48 h后，下钻检查，确认后取出填砾转换接头及管内杂物。

常规方法充填滤料时，滤料在井管与井壁之间极易形成“架桥”现象，且滤料密实度低，尤其是在井壁质量差或者中深井施工时，滤料填充质量更差；而新型投砾方案采用管内投砾，使用管内投砾专用接头管让滤料充填至管外目的层的环状间隙。无论井的深度多少、井壁环状间隙有多小，都能简单快速的将滤料充填至目的层位，大大提高了成井效率和成井质量。

2 水文水井管建模与仿真

首先对投砾模型进行参数化建模，并对仿真流程进行阐述说明，最后针对不同参数的模型进行仿真，从而实现多个参数的灵敏度分析。

2.1 水文水井管建模

为优化井管参数，需对多参数下的井管模型性能指标进行仿真分析，性能指标主要为投料时间以及井管强度。为简化多组模型的3D建模过程，采用Cero4.0软件对井管、井壁以及投砾管等主要部件进行参数化建模，并将井管内导流板水平倾角(用A表示)以及井管开孔横轴和纵轴长度(分别取用H和V表示)作为可变参数。结合实际尺寸，三个可变参数的取值范围分别为30°～60°、30～60 mm及30～60 mm。部分模型如图3所示。

2.2 水文水井管静强度仿真

对井管模型进行网格划分，设置合适的材料参数以及约束条件，最后进行静力分析，网格划分的效果图及静力分析的应力云图分别如图4、图5所示。

图4中网格稀疏部分为井管内部导流板区域。从图5中可以看出，井管应力最大的地方集中在不规则区域，即井管开口处，应力大小为3.7 MPa，取井管动载与静载安全系数1.4及1.2，结合HT200铸铁的许用应力值200 MPa得到许用应力值为119 MPa，远大于计算得到的最大应力值。

2.3 水文水井管投砾性能分析

为仿真得到不同参数下井管的砾料速度，可采用Fluent软件中的多相流模型进行计算。Fluent软件中的多相流模型包含VOF(Volume of Fluent)、MIXTURE和Euler模型。由于投砾量大，且仿真过程为颗粒流动的过程，为了得到精确的仿真结果，本文需采用Euler模型中的DDPM(Dense Discrete Phase Model，稠密离散相模型)[5]。

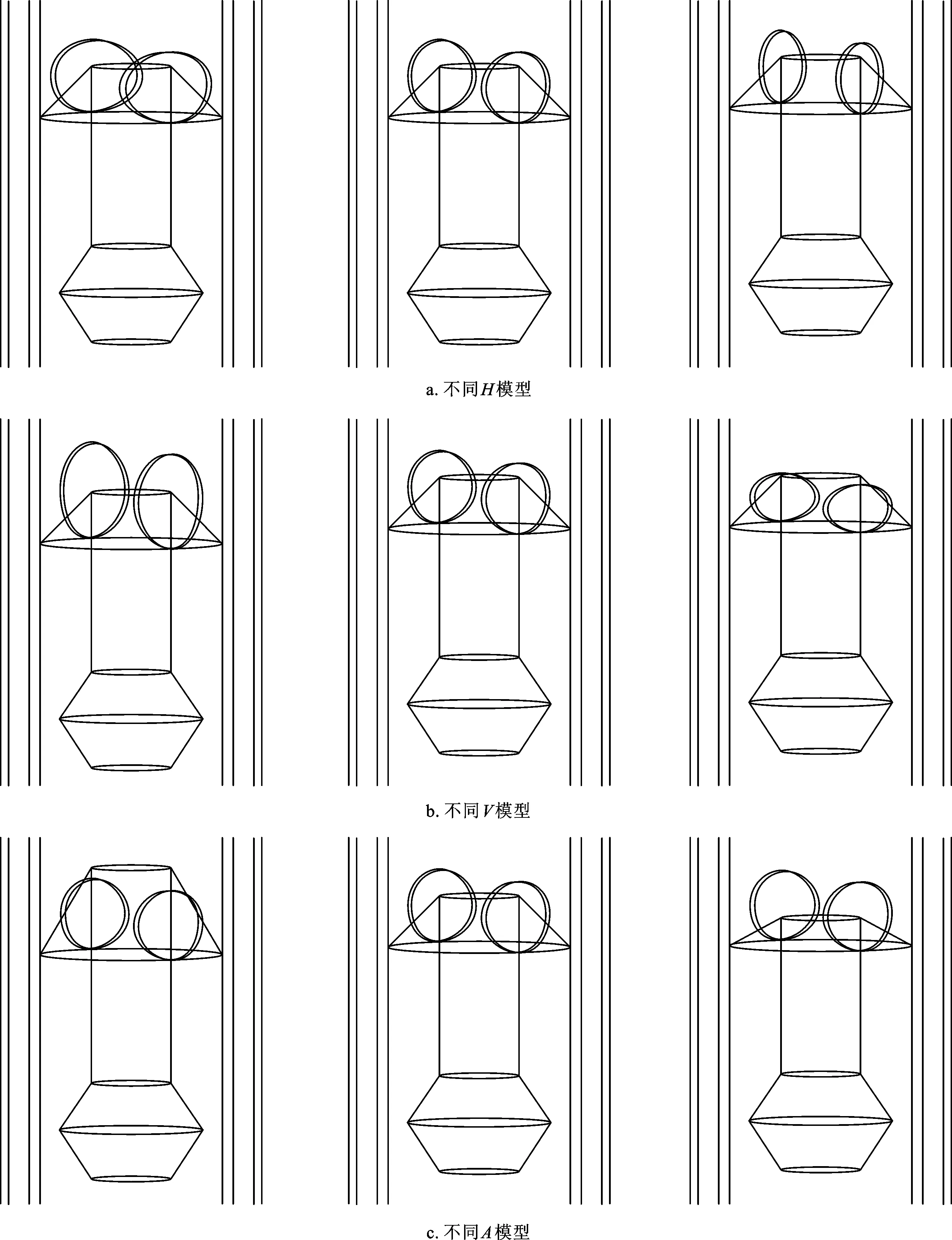
图3 不同H、V、A模型Fig.3 Different H、V、A models

图4 静力分析结构网格Fig.4 Structure grids of static analysis

图5 井管静力分析应力云图Fig.5 Stress cloud diagram of well pipe static analysis

图6 流场网格模型Fig.6 Grid model of flow field

对井管内流场模型进行网格划分得到网格如图6所示。设置合理的求解模型。选择基本的Laminar(层流)模型。多相流模型选择欧拉模型，并勾选DDPM选项。在选好模型后分别设置材料属性参数、颗粒属性参数、边界条件，求解参数之后再进行求解计算，得到仿真过程的残差监视图(图7)。

图7 流体仿真残差监视图Fig.7 Residual error monitoring chart of fluid simulation

从图7中可以看出，随着计算的逐步迭代其过程逐步趋于收敛，说明在一段时间后，系统的流进与流出达到稳定平衡。选取井管竖直剖面观察其离散相分布云图，如图8所示。

2.4 水文井管各参数灵敏度分析

为探究H,V,A(分别指开孔处水平尺寸、竖直尺寸和导向弧板角度)三个参数对于井管强度σ的影响，分别控制其中的两个参数，改变第三个参数进行静力分析，得到各参数对强度的灵敏度曲线，如图9所示。

从图9可以看出，开孔处井管强度主要受开孔直径的影响，随着开孔处水平尺寸增大，其最大应力随着尺寸的增大而增大，且最大值小于计算许用应力值。随着开孔处竖直尺寸增大,其最大应力随着尺寸的增大而减小，且最大值小于计算许用应力值。这是由于当开孔处水平尺寸固定时，随着开孔处竖直尺寸的增大，开孔左右两边受力最大处曲率增大，应力集中效应减小；当竖直尺寸趋于井管全长时，应力最大值趋于不开孔时的应力值大小。导流板角度对开孔处井管强度影响几乎忽略不计。

同样的方法可以得到H,V,A三个参数对砾料速度的灵敏度曲线，如图10所示。从图10可以看出，砾料速度受开孔直径和导向弧板角度双重叠加影响,随着之间的空间减小，从而使得砾料难以通过，当到达某个角度后砾料会出现堵塞。

图8 砾料速度云图(单位：m/s)Fig.8 Cloud diagram of gravel velocity

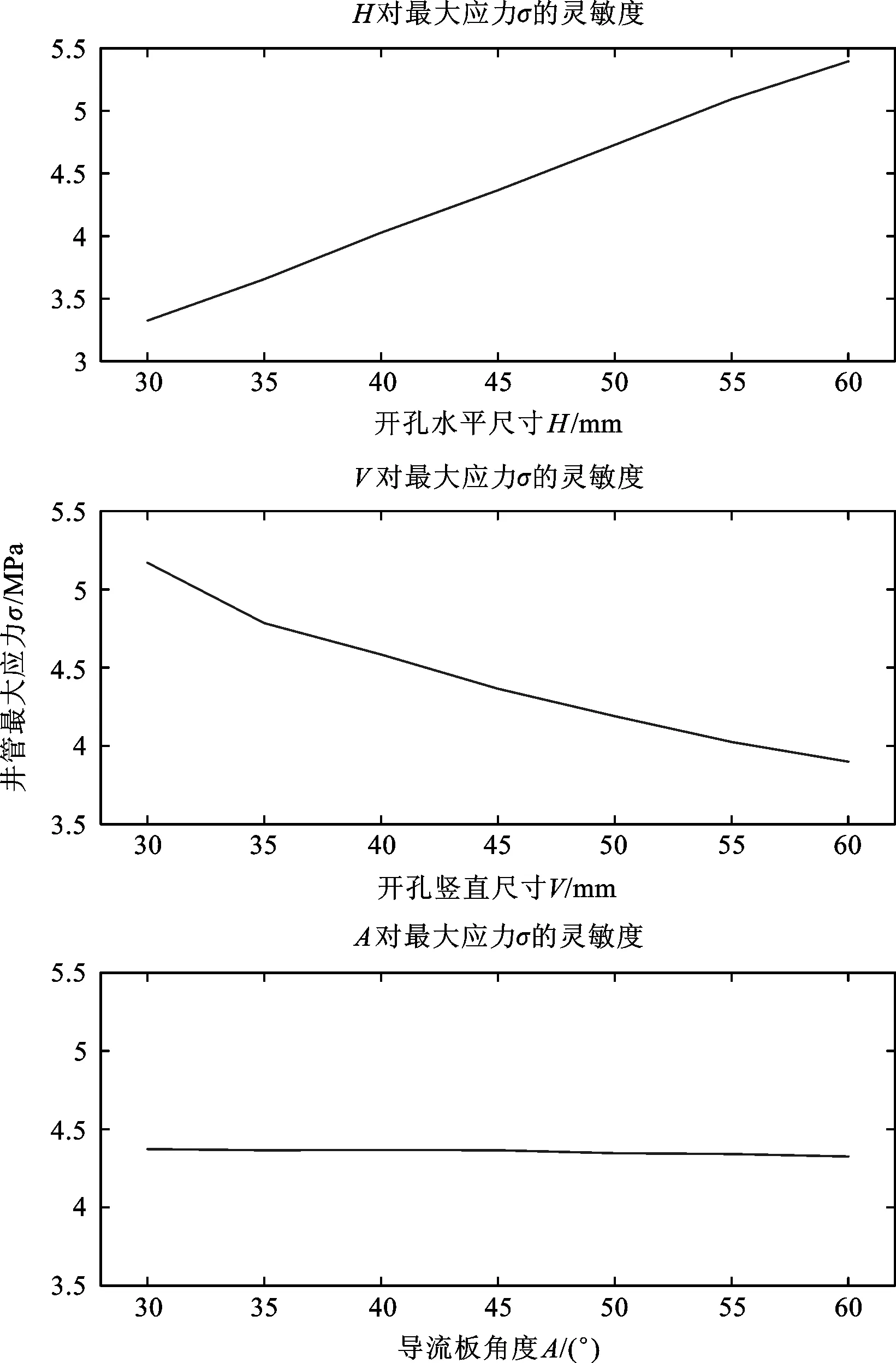
图9 水文井管静强度灵敏度分析图Fig.9 Sensitivity analysis diagram of static strength of hydrological well pipe

开孔处水平尺寸增大或者开孔处竖直尺寸增大，砾料流动速度逐渐增大，这是因为随着开孔尺寸的增大，开孔面积增大，提高了砾料的通过性。随着导流板倾斜角度的增加，砾料流动速度先增大随后减小，出现这一现象的原因是，当导流板角度增大后，更陡的坡度会加速砾料的通过，但是当角度过大时，导流板和井管内壁

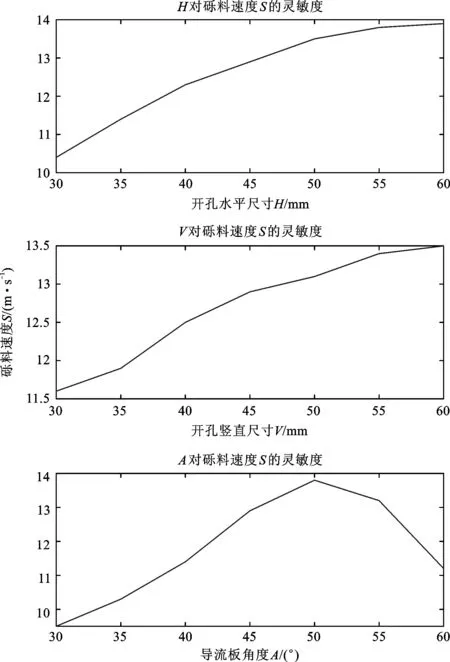
图10 水文井管砾料速度灵敏度分析图Fig.10 Sensitivity analysis diagram of gravel throwing speed of hydrological well pipe

3 水文水井管结构参数优化设计

3.1 响应曲面优化

响应曲面法对于多因素多水平试验的优化问题具有良好的适应性，因此可将之应用到仿真结果，从而得出综合最大应力σ与最大砾料速度S双优化目标下的最优目标响应值[6]。

响应曲面法实现的核心通常有中心复合设计(Central Composite Design,CCD)与Box-Benhnken(BBD)设计两种。CCD比BBD实验能更好地拟合相应曲面，但是CCD设计过程中，有很多点会超出原定的水平，在超出原定水平不会产生危险的条件下，优先采用CCD设计，本文选取CCD设计更为合理[7]。为得到综合两个响应下(即井管强度与投料性能)的三参数优化结果，可采用目前常用的合意性函数法来实现[8]。这种方法实现的核心是将多目标优化问题通过合意性函数转化为单目标优化问题[9]。合意性函数法的原理：首先赋予每一个目标响应一个合意性函数，函数值域为[0,1]，函数自变量为响应值，令其定义域(即响应值取值范围)为[l,u]，函数值越接近1表示优化输出结果越理想[10]。对于望小型目标优化指标，其合意性函数为：

(1)

式中：y为自变量响应值，当响应值大于其取值范围时(y≥u)，合意性函数为0，当响应值小于其取值范围时(y≤l)，合意性函数为1；r为接近因子，其大小体现为响应值接近最小值u的重要程度。

对于望大问题的合意性函数为：

(2)

式中各参量含义同式(1)。

常用合意性函数如式(1)、(2)所示。面向本文所研究的最大应力σ与最大砾料速度S双目标优化问题，其中最大应力σ为望小问题，该指标存在上下限，越接近下限值，合意性函数值越接近1，同时小于下限值时均为1；越接近上限值，合意性函数值越接近于0，同时当大于上限值时，均为0。对于砾料速度，属于望大问题，与望小问题相反。上述双目标分别为单一合意性指标，无法综合考量双目标的相互影响，因此采用附加有不同权值的组合合意性函数将两个单目标问题转换为一个单目标问题。

最大应力σ以及投砾时间T均为望小问题，在得到两个响应的合意性函数之后，考虑各函数权重w1,w2，得到整体加权集合均值作为整体合意性：

(3)

至此将双目标的优化问题转化为了单目标的优化问题，随即便可在可行域采用单目标极值优化算法得到合意性函数的最大解。通过软件分析，得到双目标响应的总体优化结果，如图11所示。

图11 优化合意性图Fig.11 Optimizing desirability graph

从合意性函数的值可以看出，总体合意性为0.976 5，参数优化结果较为理想，得到优化结果为水平开孔H=30 mm，竖直开孔V=60 mm，导流板角度A=48.18°。计算拟合曲面下的三个响应值后，得出最佳参数及相应的响应值如表1所示。

表1 优化结果汇总Table 1 Summary of optimization results

由于井管最大应力较小，远小于许用应力值119 MPa，因此其合意性值较小对优化结果影响较小，砾料速度的合意性值接近1，表明其优化结果可靠。

3.2 优化结果验证

利用Cero软件得到最优参数下的模型进行静力学仿真以及Fluent流体仿真，得到的结果与优化结果进行对比，其中最优参数下的静力分析及流场分析结果分别如图12、图13所示。

将图12与图13中得到的结果与优化结果进行对比，可得到表2。从表2中可以看出，优化结果与仿真结果接近，一定程度上验证了研究的正确性。

图12 静力学仿真云图Fig.12 Statics simulation cloud map

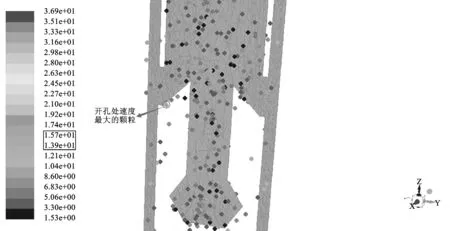
图13 流场仿真云图Fig.13 Flow field simulation cloud map

表2 仿真与优化结果对比Table 2 Comparison of optimization and simulation results

4 结论

(1) 本文提出一种中深孔水文水井新型管内投砾成井工艺，针对其核心元器件投砾管接头总成，采用Fluent软件中的多相流分析模型及Ansys软件中的静力分析模块，进行结构参数优化设计，得出核心元器件的最佳开孔尺寸(以外径127 mm井管为例)和导向弧板的斜坡角度：H=30 mm，V=60 mm，A=48.18°。最后对最优参数下的结构模型进行静力学仿真及Fluent流体仿真，对比优化及仿真结果可知，优化结果可靠，验证了研究的正确性。

(2) 与常规填砾工艺相比较[4]，管内投砾工艺不受井壁质量和环状间隙大小的影响，通过管内投砾专用接头管，能高效安全的将滤料从井管内充填至井管外目的层处的环空间隙，减少了成井环节和成井周期，技术方案可靠，具有较高的经济效益、广阔的应用市场和发展前途。

(3) 管内投砾施工工艺和新型井管投砾结构已分别获批国家发明专利和国家实用新型专利，且在湖北省内生活用水井和国家地震台网地下流体监测井工程中成功应用，并取得较为显著的经济社会效益，该工艺可推广应用于深水井、地热井、监测井等工程。