动点的牵连运动分析与运动合成定理推证

高宗战 刘 伟 高行山 张劲夫 刘永寿 支希哲

(西北工业大学力学与土木建筑学院，西安 710072)

点的合成运动作为理论力学的重要知识点，不但是后续刚体平面运动的理论铺垫，而且其所蕴含的“分解-合成” 的研究方法也需要重点给学生阐述。国内大部分理论力学教材中关于运动学中点的速度合成定理的推导，是基于一个动点在动系中做任意运动的矢量图模型，通过平均速度取极限的方法形成的速度矢量三角形来得到的。该方法最早是由伏龙科夫著的理论力学教材[1]引入，具有简明直观的优点，但是仍然存在两个不容忽视的问题：(1)由于牵连点是一个不断变动的点，直接用位移求导的方法计算牵连速度容易被学生误解。(2)后续合成加速度的推导，是基于矢径求导的方法获得的，造成速度与加速度合成推导在方法上不衔接，给学生带来疑点：为什么在速度合成定理中未采用该方法？因此，点的合成运动一直是理论力学教学中的关注点和争论点。针对速度合成定理，给出更加严谨一致的推导方法是理论力学教学工作者的责任。

国内广大的理论力学工作者针对该问题，提出了不少解决方案。陈立群[2]对欧美理论力学教材中的运动学进行了剖析。胡浩等[3]通过“跟踪牵连点”方法，将某瞬时的牵连点与动点从空间位置上“分离”。王维等[4]引入“耦合位移” 的概念改进现行大多数教材中普遍采用的点的复合运动速度合成定理的几何法推导。牛聪民[5]提出用复数量去区分“动系中观察者的观测结果”和“定系中观察者对动系中观察者观测结果的测量”，上述有的方法由于数学要求较高，不易被学生理解，未获得教材上的广泛采用。有的方法是采用刚体平面运动的概念指出牵连速度[6]，该方法的缺点是知识顺序的跳跃，不宜教学使用。本文避免了上述问题，给出了形式上一致且易于学生理解点的速度和加速度合成定理的推证过程。

1 牵连速度和加速度的解析表达

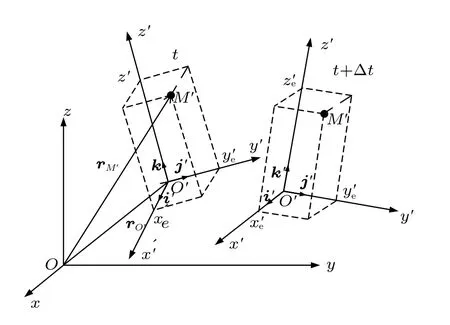
图1 牵连点M′ 在两个不同时刻的位置状态

2 速度合成分析

固定坐标系为Oxyz，动系为O′x′y′z′，动点M在动系和定系中均作任意运动，运动模型如图2 所示，以矢径rM和r′M分别表示动点M在定系上和在动系上的位置矢径；rO′为动系坐标原点O′在定系上的位置矢径，设动点M在动系上的坐标为(xr,yr,zr)。

图2 合成运动速度分析模型

动点M的绝对矢径可以表示为

即采用解析法获得的速度合成定理。

3 加速度合成分析

图3 中矢径rM和r′M分别表示动点M在定系中和在动系中的位置矢径；rO′为点O′在定系中的位置矢径。动点M的绝对加速度为

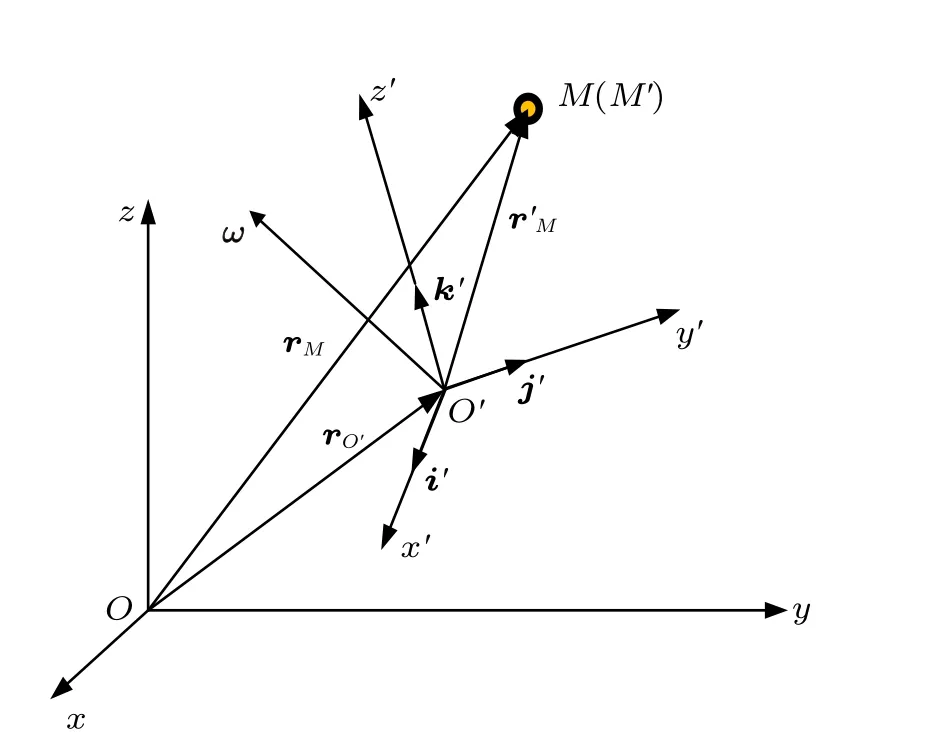
图3 合成运动加速度分析模型

式中，将2ω×vr记为aC，称为科氏加速度。式(17)表示，动点M的绝对加速度等于牵连加速度、相对加速度与科氏加速度的矢量和，即点的加速度合成定理。

4 结论

本文对动点的牵连运动进行了再分析，并采用解析方法推证了点的速度和加速度合成定理，获得的主要结论如下。

(1)从动系上看牵连点和从动系上观察动点，是两个不同的概念。任意瞬时，牵连点是动系上的某一“固定点”，相对于动系不运动，但是动点相对于动系存在相对运动。

(2)牵连点M′为动系上与动点M相重合的点，但是由于从动系上观察牵连点和动点存在区别，因此，两者坐标相同，但坐标的导数并不相同。

(3)本文指出上述两点差异后，对动点和牵连点的区分更加直观，在速度和加速度合成时采用解析方法推证，易于学生理解和教学。