考虑机组功率因数的分布式风机选址定容研究

陈 巍,杨 兵,朱益民

(国网扬州市江都区供电公司，江苏 扬州 225002)

1 引言

随着分布式电源在电网的渗透率逐渐提高，以风机、光伏发电为代表的具有波动性、不确定性的新能源接入电网对电网的网损影响不容忽视。分布式电源的配置位置和和安装容量都对整个网络的网损有着较大影响[1]，因此分布式电源的选址定容优化显得尤为重要。本文着重研究机组的功率因数对于机组的选址定容优化的影响。目前已有研究一般假设DG 机组按照固定功率因数运行或不考虑机组提供无功支撑，仅研究此情况下的DG机组的选址和定容，没有考虑最优功率因数对于DG机组在减少网损中的作用。

目前针对分布式电源选址定容的研究较多，夏澍等人建立了分布式电源选址定容的多目标决策模型[2]。徐迅等人在微网多类型分布式电源选址定容规划时考虑了环境成本和时序特性[3]。叶萌等人在分布式电源选址定容时考虑了电压质量的影响[4]。海晓涛等人提出了基于免疫遗传算法的智能配电网分布式电源选址定容[5]。芮松华等人基于遗传-蚁群算法对交直流配电网分布式电源优化配置进行了研究[6]。张沈习等人在选址定容时考虑了相关性和间歇性[7]。赵兴勇等人分析了分布式电源选址定容优化算法[8]。可以看出，较多文献从分布式电源选址定容的算法、求解目标、约束条件等方面进行了分析，但是很少有文献研究机组的功率因数对选址定容的影响。

为此，本文考虑机组的最优功率因数，对分布式风机进行选址定容的优化。首先建立了网损的数学模型，得出了网络有功网损和无功网损的公式；随后分析了功率因数对机组选址定容的影响；然后说明了本文所提机组选址定容的具体方法，从确定机组位置、容量到功率因数。最后结合IEEE30节点系统进行了算例分析，说明了本文所提方法的有效性。

2 配网网损模型

N节点的网络内总的有功和无功损耗可用下式计算[9]：

其中，

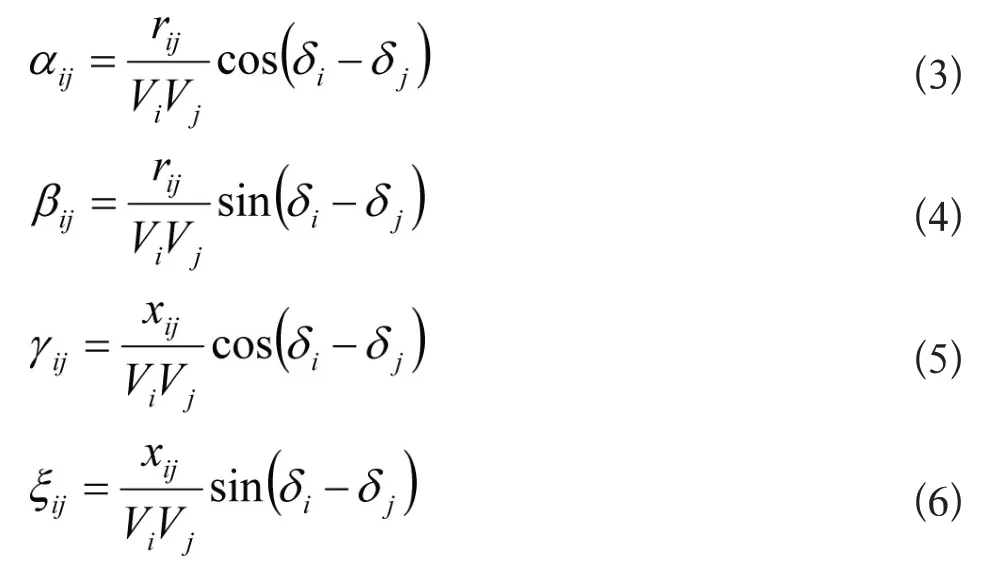
Vi∠δi为节点i的电压；rij+jxij=Zij为阻抗矩阵[Zbus]的第ij个元素；Pi和Pj分别为节点i和j的有功注入；Qi和Qj分别为节点i和j的无功注入。

装有风机组的节点i的总有功和无功注入关系式如下：

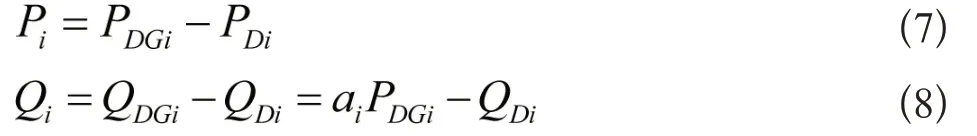
其中，QDGi=aiPDGi；PDGi和QDGi分别为风机组注入节点i的有功和无功；ai=(sign)tan(cos-1(pfDGi))，sign=±1：风机注入无功时，sign=+1；风机消耗无功时，sign=-1；PDi和QDi分别为节点i的负荷有功和无功；pfDGi为i节点风机的运行功率因数。

将式(7)和(8)带入(1)和(2)，得到总的有功和无功功率损耗如下：

3 功率因数对机组选址定容的影响

根据公式(7)和(8)可知，有功和无功损耗是PDG和a的函数。这两个变量对配网网损有很大影响。下图给出了有功损耗与DG机组容量、功率因数的变化关系[10]。

从图1中可以得知，对于某一确定的功率因数，有功网损与风机的容量首先成反比关系，网损最小点即是风机最优容量。随着风机容量的增加，有功网损也上升，两者呈现正比关系。类似地，对于给定风机容量，网损最小时可得到最优功率因数。相似的结论对于无功网损同样适用。因此，风机配置在合适的容量、运行于最优功率因数对于减少系统网损是至关重要的。

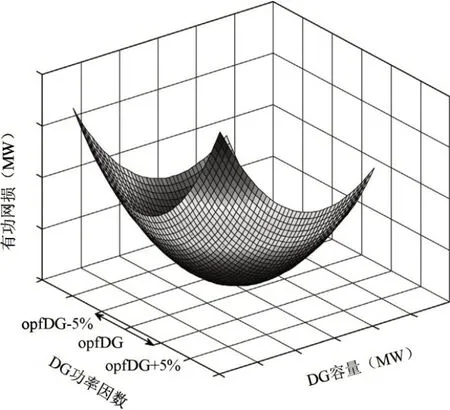
图1 位置和功率因数对系统有功损耗的影响

4 考虑功率因数的风机选址定容

4.1 风机选址方法

根据网损在有功注入各节点i 的变化情况用来确定风机的位置。由于某节点安装风机后会增加该节点的有功注入，使得该节点对有功网损的灵敏度为负的最大节点为最佳的风机安装位置，从而能够在该节点减少网损的量最大。

4.2 风机容量确定方法

以网损最小为目标的节点i的风机容量为：

其中，

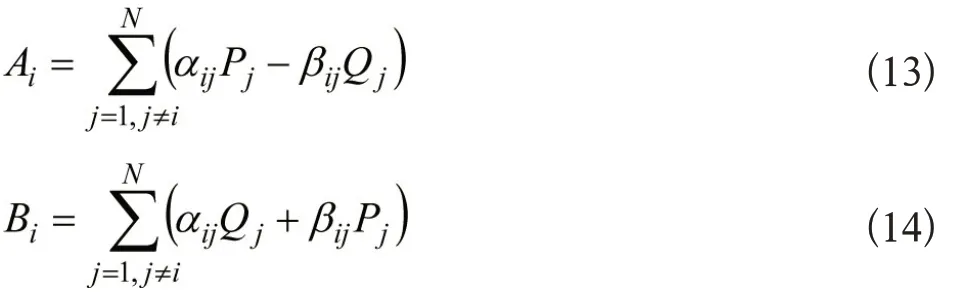
ai由式(7)(8)确定。

该式适用于当pfDGi或者ai已知时，确定不同风机的最优容量。风机等DG 机组的功率因数取决于运行条件和DG类型。通过设置pfDgi的参数值可以确定各节点风机的最优容量。

4.3 风机最优功率因数确定方法

对电力系统的常规负荷，功率因数一般为滞后的感性特性，功率因数在0．7-0．95之间，因此，风机的最优功率因数应当滞后。本文假设负荷的功率因数均为滞后的。

上式确定了机组的最优有功和无功容量。式(11)和式(12)分别确定了机组的最优有功和最优无功容量，节点i 的机组同时注入有功和无功便可得到机组的最优容量，即：

本式也说明，风机能够在总系统损耗最小的节点i同时提供有功和无功。

因此，对于安装于网络内的风机，节点i的机组的最优功率因数为：

5 算例分析

5.1 算例说明

本文选择IEEE30节点[11]系统进行仿真。考虑到负荷时变性、风电机组运行条件等特点，可以使得风机以最优出力同时减少网损。风机分为可调度、不可调度两种，本文考虑可调度风机。本文的负荷曲线如图2所示，根据负荷曲线来调整可调度风机的出力使得网损达到最小，整个网络的损耗便可由风机出力曲线确定。另外，本文原始网络的网损曲线如图2和图3所示。

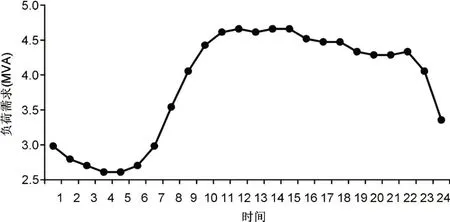
图2 负荷需求曲线

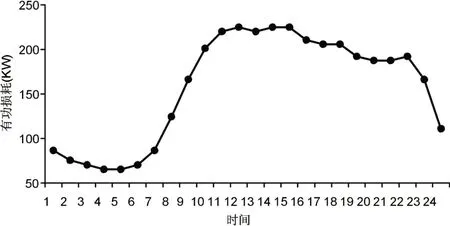
图3 网络有功损耗曲线

5.2 算例分析

本文具体计算步骤如下：

1、计算峰荷水平下的基线负荷潮流，利用式(1)计算总有功损耗；

2、仅计算峰荷水平下的风机最优选址、功率因数；

a)利用式(11)计算各节点最优容量、最优功率因数；

b)将之前得到的风机逐一配置在各节点，利用式(7)计算风机在各个节点的功率损耗；

c)确定使节点网损最小的最优机组容量或者节点最大输出。

3、确定t时刻机组在最优位置的最优输出功率。

4、对各个时刻进行步骤3的同样操作，计算总的网损。

由此，本文计算结果如表1。风机最优节点为17，最优容量为2．222MVA，最优功率因数为0．82(滞后)。

表1 计算结果

各时刻的机组容量配置和机组有功网损曲线如图4和图5所示。

图4 机组容量计算结果

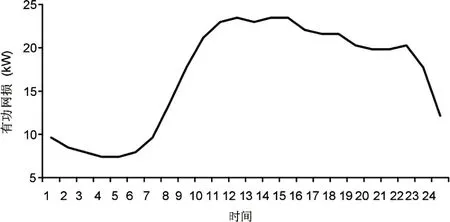
图5 机组有功网损计算结果

可以看出，DG机组的容量配置随时间的变化与负荷需求大致类似，机组的有功网损随时间的变化也大致与网络的有功网损变化趋势一致。

6 结束语

本文首先建立了网损的数学模型，得出了网络有功网损和无功网损的公式；随后分析了功率因数对机组选址定容的影响；然后说明了本文所提机组选址定容的具体方法，从确定机组位置、容量到功率因数。最后结合IEEE30节点系统进行了算例分析，根据算例，详细阐述了本文的计算步骤，确定了机组的最优位置和容量以及功率因数，说明本文所提方法的有效性。