跌落式冲击试验台后峰锯齿冲击数值分析与试验研究
2022-03-11朱升贺牛金皓李维维
朱升贺,方 东,牛金皓,杨 锐,孙 溢,李维维,曹 迅
(南京晨光集团有限责任公司,南京 210006)
0 引言
航天产品在装卸、运输、机动和发射等过程中会经历各类复杂冲击环境的考验,故须对航天产品进行冲击环境试验,以考核产品的功能可靠性。国内外在冲击环境试验中广泛采用规定一种冲击运动的试验方法,即由加速度峰值、冲击脉宽、速度变化量等参数确定一种波形(如半正弦波和后峰锯齿波)并规定其容差范围,然后通过冲击台对产品进行各种严酷等级的冲击试验。半正弦波(GJB 150A 已取消半正弦冲击)多用于模拟线性系统的撞击和减速所引起的冲击效应,如弹性结构的碰撞;后峰锯齿波比半正弦波具有更均匀的频谱,主要用于模拟系统的非弹性碰撞。
目前,国内外常采用铅块配合跌落式冲击试验台的方式开展后峰锯齿冲击试验,即利用铅块受压时的非弹性,通过改变铅块的尺寸和形状得到不同量级的后峰锯齿波形。梁志恒对锥形铅块压缩模型进行简单计算,并通过后峰锯齿试验验证了理论推导的正确性。日本吉田精机株式会社的ASQ系列冲击台采用锥形铅块作为后峰锯齿波形发生器,结果发现当铅锥底面积不变时,后峰锯齿波脉宽随着锥角的增大而减小。刘陆广等以现有铅锥为参考,利用仿真分析软件优化铅锥形状,可实现3.5 t 产品的后峰锯齿冲击试验。梁斌强利用有限元软件对摆锤式冲击台的后峰锯齿冲击进行动力学分析,并通过试验验证了其仿真分析的准确性。张明波研究了铅块形状分别为圆锥体、圆台体、圆柱体的冲击响应模型,结果表明圆锥体铅块可获得较好的后峰锯齿波形,且随着铅锥锥角的增大,响应加速度峰值增大、脉宽减小。
由于后峰锯齿冲击后要求加速度迅速降至0,所以后峰锯齿波形的产生和调试比半正弦波困难,且为获得试验要求的冲击波形,试验前须铸造不同规格的铅锥进行标定,不仅费时费力,还会损害试验人员健康。为了降低后峰锯齿冲击试验的风险和成本,提高试验效率,本文对跌落式冲击试验台后峰锯齿冲击进行数值分析与试验研究,构建后峰锯齿冲击波形库,以期为形成后峰锯齿波形控制的标准方法提供技术参考。
1 后峰锯齿冲击试验原理
后峰锯齿冲击波的波形没有变形后的恢复阶段,代表作为波形发生器的材料或结构在达到某一变形量后突然失去了抵抗变形的能力。目前通常采用冲击铅锥法,利用铅锥受压时的非弹性产生瞬态波形(即后峰锯齿冲击波)。图1 所示为后峰锯齿冲击脉冲波形及容差要求。
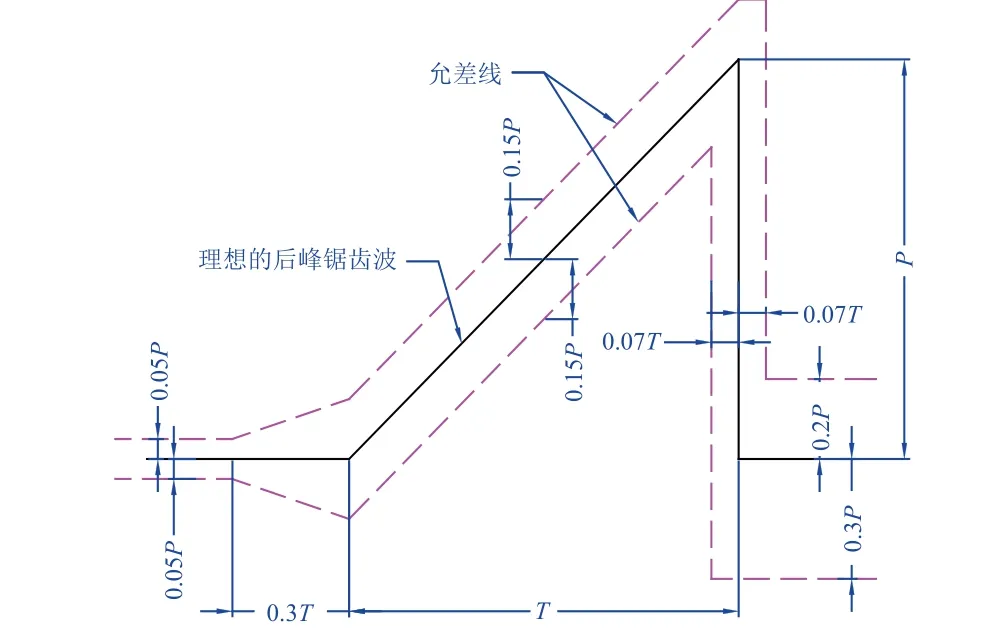
图1 后峰锯齿冲击脉冲波形及容差要求Fig. 1 Waveform of a typical final peak sawtooth pulse and the tolerance
跌落式冲击试验台(如图2 所示)产生后峰锯齿冲击波的原理是:产品固定在冲击台面上,将台面提升至特定高度后突然释放,使产品和台面一起跌落在铅锥上;从台面接触铅锥时起,台面向下运动受阻产生一个与重力方向相反的加速度,同时铅锥发生塑性变形,加速度近似于线性增加;当铅锥达到某一变形量后加速度突然降至0,即响应加速度曲线呈现后峰锯齿波形。试验过程中通过数据采集系统采集冲击信号进行处理和分析。

图2 跌落式冲击试验台Fig. 2 The drop-type shock test bed
2 后峰锯齿冲击响应模型
铅锥的压缩物理模型如图3 所示,设铅锥为理想刚塑性体,且铅锥被压缩过程中遵循体积不变定律,即塑性变形前的体积与变形后的体积相等。
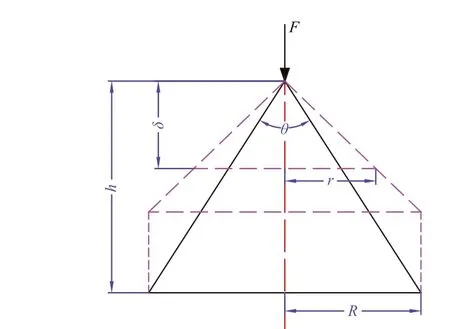
图3 铅锥的压缩物理模型Fig. 3 Model of compression for the lead cone


设冲击块质量=100 kg,铅锥锥角=55.3°,通过以上数值分析模型求解得到如图4 所示的不同跌落高度下的冲击响应加速度。可以看到,随着跌落高度的增大,响应加速度峰值增大、脉宽减小。
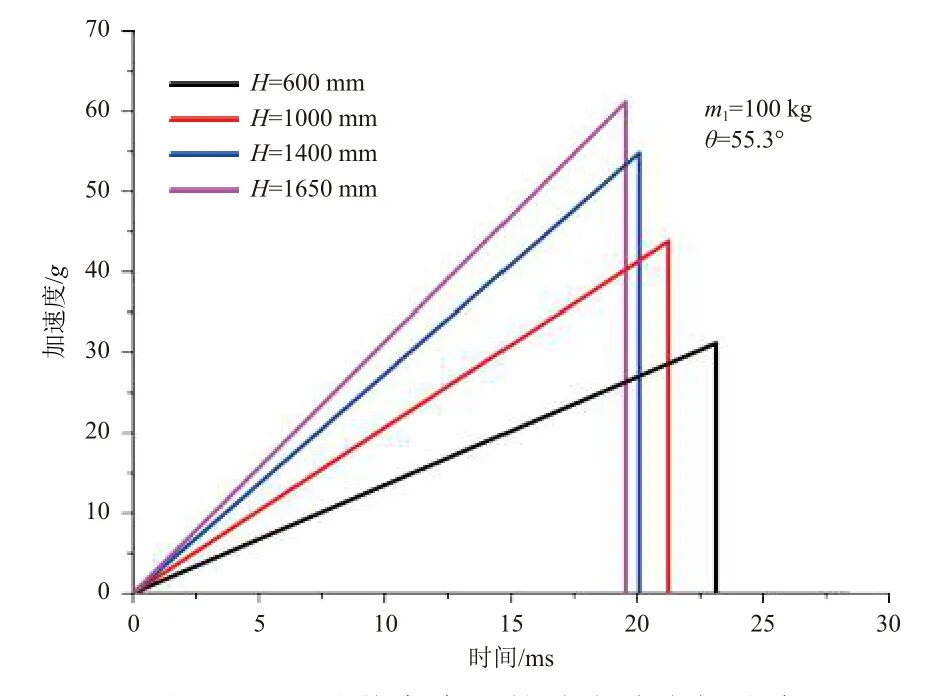
图4 不同跌落高度下的冲击响应加速度Fig. 4 Responsive acceleration curve for different drop heights
设冲击块质量=100 kg,跌落高度=500 mm,通过以上数值分析模型求解得到如图5 所示的不同铅锥锥角下的冲击响应加速度。可以看到,随着铅锥锥角的增大,响应加速度峰值增大、脉宽减小。
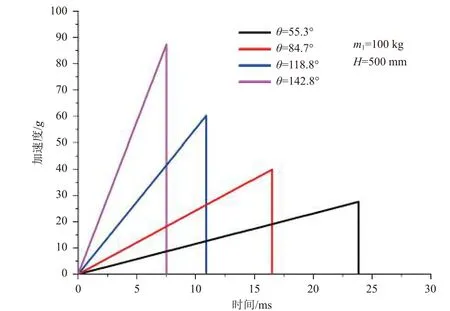
图5 不同铅锥锥角下的响应加速度Fig. 5 Responsive acceleration for different lead cone angles
3 后峰锯齿冲击试验
跌落式冲击试验台后峰锯齿冲击波形的影响因素包括跌落高度、铅锥锥角及铅锥底面直径等。这些影响因素在试验中关系错综复杂,本文通过控制变量法对各影响因素进行分析,固定冲击块质量(100 kg)和铅块屈服应力(5 MPa),进而构建后峰锯齿冲击波形库。
3.1 跌落高度的影响分析
铅锥在冲击过程中发生塑性变形,其模型见图6(锥角42.3°、底面直径65 mm)。通过跌落式冲击试验台进行冲击试验,跌落高度依次为500 mm、900 mm、1100 mm、1500 mm、1700 mm,生成的响应加速度曲线如图7 所示。可以看出:在不同跌落高度下,响应加速度曲线均呈现良好的后峰锯齿波,在冲击时间历程内,加速度上升段时间占比较大,下降段垂直度较高;但不同跌落高度下的后峰锯齿波差异性显著——随着跌落高度的增大,响应加速度的峰值不断增大,冲击脉宽缩小,速度变化量增大。

图6 铅锥模型Fig. 6 The lead cone model
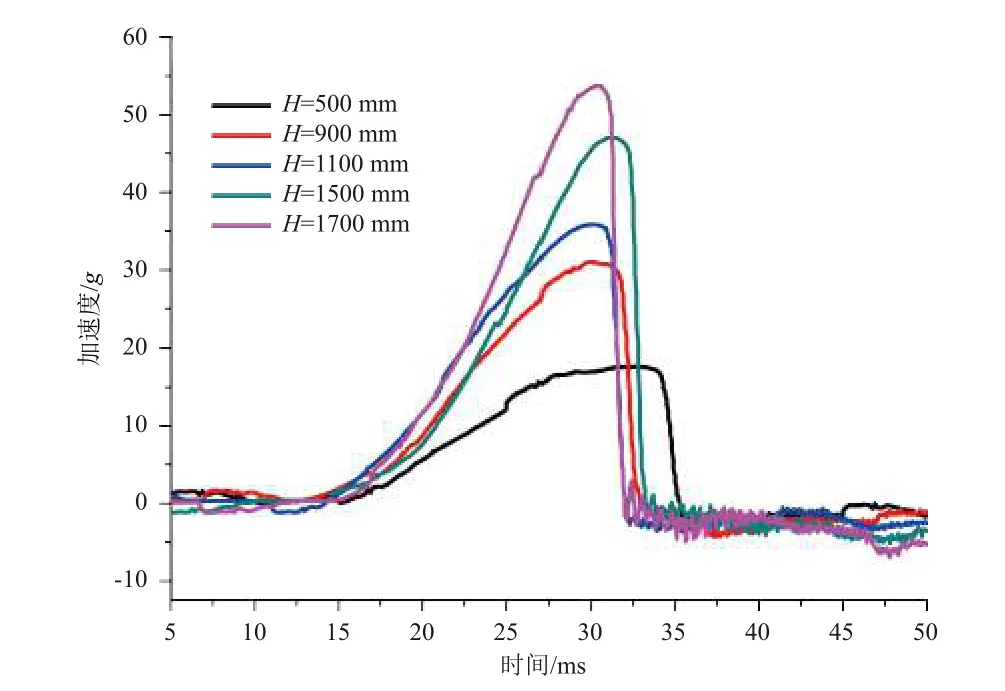
图7 不同跌落高度下的冲击响应加速度曲线Fig. 7 Acceleration curve of shock response for different drop heights
3.2 铅锥锥角的影响分析
基于跌落高度对冲击响应的影响结果,继续研究铅锥锥角对冲击响应的影响。3 种铅锥锥角分别为42.3°、100.1°、142.8°,跌落高度为600 mm 时的响应加速度曲线如图8 所示。可以看出,在相同的跌落高度下进行冲击试验,铅锥锥角越大,响应加速度的峰值越大,冲击脉宽越小,速度变化量越大。
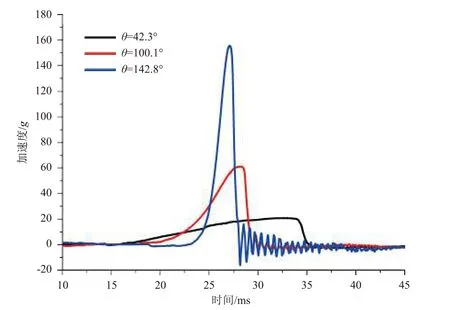
图8 不同铅锥锥角下的响应加速度曲线(跌落高度为600 mm)Fig. 8 Acceleration curve of shock response for different lead cone angles (H=600 mm)
3.3 铅锥底面直径的影响分析
基于铅锥锥角对冲击响应的影响结果,继续研究铅锥底面直径对冲击响应的影响。铅锥底面直径分别为50 mm 和65 mm,锥角均为66.1°,跌落高度依次为600 mm、800 mm、1000 mm、1200 mm、1400 mm、1600 mm 时的响应加速度曲线如图9 和图10 所示。可以看出:2 种底面直径的铅锥在不同跌落高度下生成的冲击响应曲线都呈现良好的后峰锯齿波;在相同的跌落高度下,当铅锥锥角相同时,铅锥底面直径越大(即缓冲行程越大),则冲击响应的加速度峰值越小,脉宽越大,速度变化量越小。
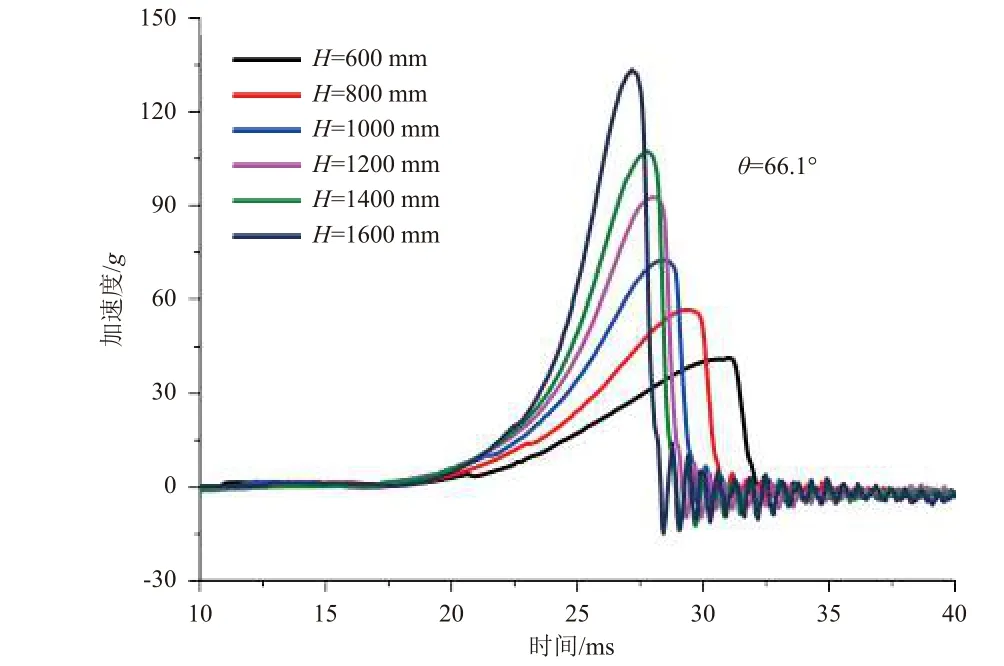
图9 铅锥底面直径为50 mm 时不同跌落高度下的响应加速度曲线Fig. 9 Acceleration curve of shock response for different drop heights (diameter of the lead cone’s bottom is 50 mm)
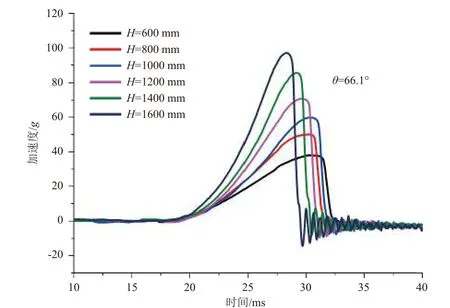
图10 铅锥底面直径为65 mm 时不同跌落高度下的响应加速度曲线Fig. 10 Acceleration curve of shock response for different drop heights (diameter of the lead cone’s bottom is 65 mm)
3.4 冲击波形库
为建立后峰锯齿冲击波形库,对8 种铅锥(为便于加工模具,减少试验误差,选择了底面直径均为65 mm 的8 种铅锥,锥角逐级增大)进行了不同跌落高度()下的冲击试验,记录冲击响应加速度峰值()、冲击脉宽()和速度变化量(Δ)随跌落高度的变化曲线,如图11~图13 所示。可以看到,随着跌落高度的增大,冲击响应加速度峰值增大,冲击脉宽逐渐缩小,速度变化量增大。在进行冲击试验标定时,应根据试验条件查询波形库中与试验量级最接近的铅锥型号和跌落高度;若连续3 次标定试验均满足试验容差要求,则可开展正式冲击试验。
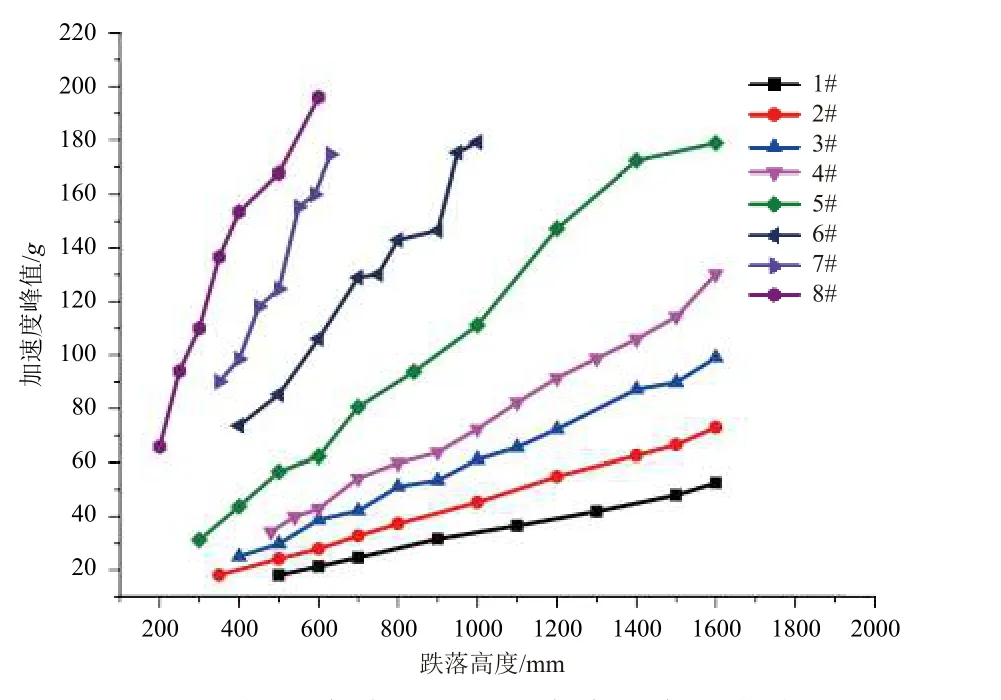
图11 加速度峰值随跌落高度的变化曲线Fig. 11 Curves of peak acceleration against the drop height
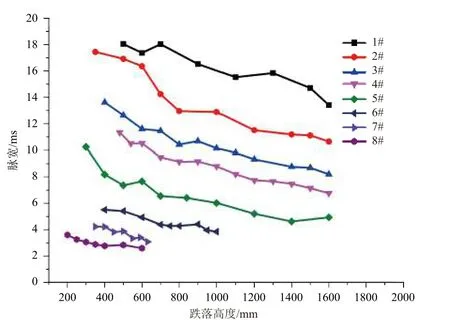
图12 冲击脉宽随跌落高度的变化曲线Fig. 12 Curves of pulse width against the drop height
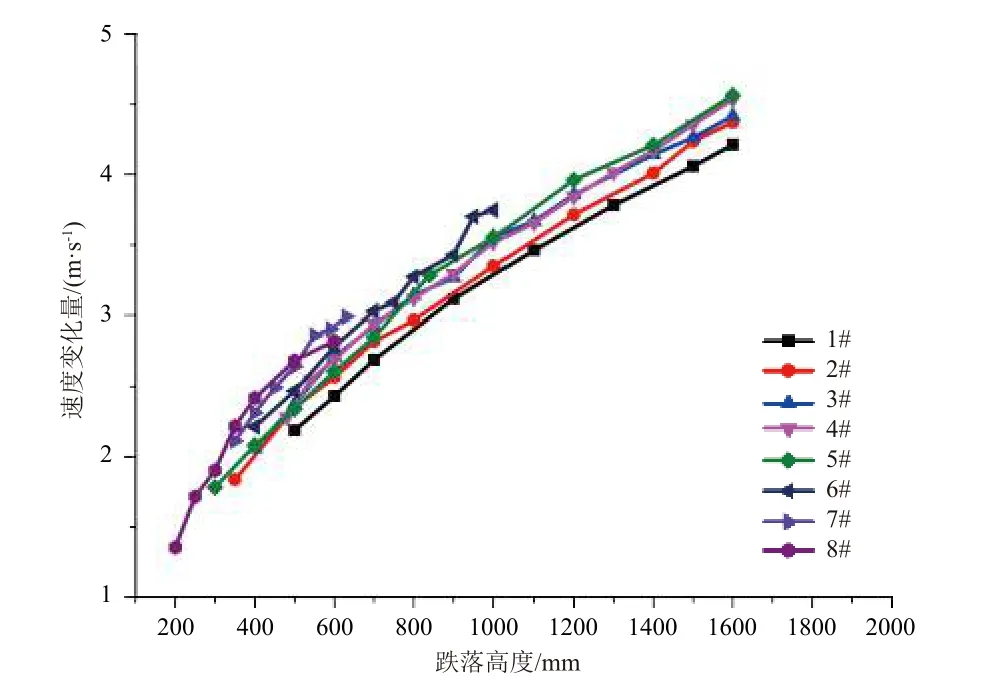
图13 速度变化量随跌落高度的变化曲线Fig. 13 Curves of speed change against the drop height
4 冲击响应模型修正
在数值分析过程中对铅锥底面半径进行了简化处理,同时未考虑冲击台跌落时受导轨的摩擦阻力,且冲击台的台面各点冲击响应存在差异,因此需通过试验结果对冲击响应模型进行修正。通过波形数据库对8 种铅锥的锥角()、跌落高度()、加速度峰值()、冲击脉宽()进行数据处理,并根据公式(11)拟合得到如图14 所示的加速度峰值与锥角和跌落高度的关系,根据公式(14)拟合得到如图15 所示的脉宽与锥角和跌落高度的关系。

图14 加速度峰值–跌落高度–铅锥锥角三维图形(黑点为冲击试验数据,曲面为数据拟合结果,拟合系数R2=0.933 67)Fig. 14 Three-dimensional graph of acceleration peak-drop height-lead cone angle (black dots are impact test data, curved surface is data fitting result with fitting coefficient R2=0.933 67)
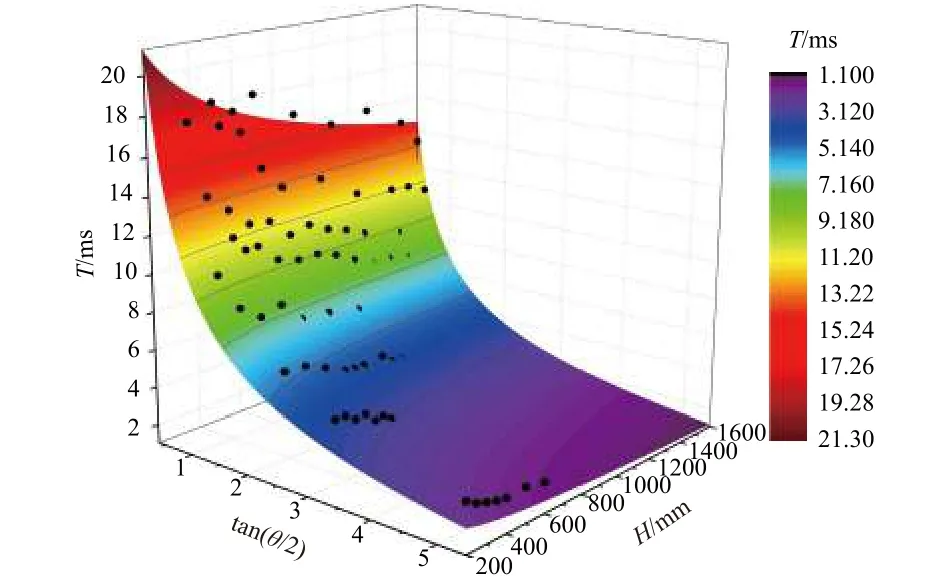
图15 脉宽–跌落高度–铅锥锥角三维图形(黑点为冲击试验数据,曲面为数据拟合结果,拟合系数R2= 0.961 05)Fig. 15 Three dimensional graph of pulse width drop height lead cone angle (black spot is impact test data, curved surface is data fitting result with fitting coefficient R2=0.961 05)
得到后峰锯齿冲击响应加速度峰值()和脉宽(ms)与铅锥锥角(°)、跌落高度(mm)的关系式:
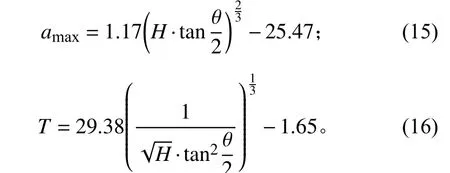
5 结束语
本文对跌落式冲击试验台后峰锯齿冲击进行了数值分析与试验研究,探讨了跌落高度、铅锥锥角、铅锥底面直径等因素对冲击响应的影响,得到了冲击响应加速度峰值以及脉宽与铅锥锥角、跌落高度的关系式。构建了后峰锯齿冲击波形库,并对冲击响应模型进行修正。经过多个型号产品的后峰锯齿冲击试验验证了波形库的实用性和便捷性,极大提高了跌落式冲击试验的效率。
