电磁微锻机构热效应模拟与实验研究

2022-03-10樊霄岳陈苏琳

工程设计学报 2022年1期

樊霄岳，刘启，官威，朱云，陈苏琳，沈彬

（1.上海交通大学机械与动力工程学院，上海 200240；2.沪东重机有限公司，上海 200129）

切削所引起的表面残余应力对航空发动机零部件有一定的危害，通常会导致零部件的强度和疲劳极限降低以及出现应力腐蚀和塑性变形，从而影响零部件的精度，严重时甚至可能导致零部件脆性断裂。喷丸强化是一种较为传统的残余应力降低方法，但该方法在降低残余应力的同时会影响工件表面的粗糙度。相较于喷丸强化，微锻是一种新颖的、具有导向结构的表面强化方法，其通过冲杆对工件表面的连续锤击来有效地降低残余应力和减小表面粗糙度［1-2］。目前，常用的微锻方法有气动锤击、超声波锤击、压电锤击和电磁锤击等［3］。

从能量输入和输出的角度来看，微锻机构实质上是一种换能机构，其可将电能先转换为机械能，再转换为材料的变形能。但是，目前针对微锻工艺的研究主要集中在影响材料表面特性的微锻机构输入参数的优化方面［4-6］，而对微锻机构工作过程中的能量变化及其性能等的研究相对较少，因而难以找到关于微锻机构能量效率、输出功率及其他动态性能优化的参考依据，这对微锻工艺的发展十分不利。目前较为成熟且存在电磁能量转换过程的换能装置包括电机、变压器等，但其对温度场、电磁场的设计要求十分严格，若设计不合理，则会导致温度异常升高，从而引发许多不利因素［7-8］。例如，Lee等［9］对永磁电机中永磁体的消磁问题进行了研究，通过建立燕尾榫机在恒定负载转矩下的退磁动力学模型，指出在进行退磁计算时应考虑热效应，这是因为退磁会导致铜损耗增加，使得电机的温度升高，从而致使其永磁体的退磁问题更加严重，严重时甚至可能导致电机失速；邰永等［10］对三相鼠笼异步电机的全域三维瞬态温度场进行了分析，指出现有电机大多是因设计时采用较高的电磁负荷而导致运行时的温升较大。温升特性是衡量电机性能的重要指标之一，其与电机的使用寿命直接相关，同时也对电机的动力、效率等性能有一定影响，因此对电机进行热效应分析尤为重要。

为了提高电机的功率密度，通常采用以下3种方法：1）合理优化电机的电磁设计，即采用高性能的电磁材料；2）适当提高电机的额定转速；3）提高电机的散热能力［11］。其中第1种和第3种方法可以推广至一般的存在电磁转换过程的换能装置的功率密度优化。本文所研究的微锻机构采用电磁锤击，主要采用第3种方法来优化其功率密度。基于此，笔者拟针对电磁微锻机构的热效应与输出功率的关系进行分析，并构建电磁微锻机构热效应仿真分析方法，最后通过实验来研究电磁微锻机构的温升特性和稳态温度特性，以验证所提出分析方法的准确性，旨在为后续通过结构优化和温度控制来提高电磁微锻机构功率密度奠定理论基础。

1 电磁微锻机构的力-磁-热耦合分析

电磁微锻机构的结构如图1所示［12］，其冲杆的往复运动是依靠周期性的安培力实现的；冲杆与线圈骨架相连，线圈骨架上缠绕均匀的多匝铜导线，用于产生周期性的电流；机构壳体上固定装有磁轭及永磁体，其产生的磁场可使通电线圈受到安培力；冲杆的芯轴通过2个直线轴承进行导向，并通过机构壳体上的限位构件（上、下限位块）进行限位。

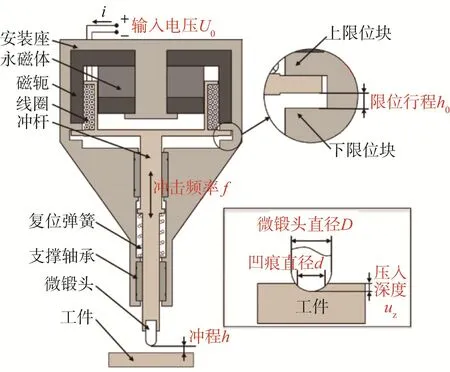
图1 电磁微锻机构结构示意Fig.1 Structure diagram of electromagnetic micro hammer peening mechanism

电磁微锻机构通常安装在机床或机器人上，而工件则被固定在夹具上。电磁微锻机构通过控制路径的进给运动，在工件表面锤击出多个连续轨迹。通过改变交流电源的输入电压、输入频率和冲程，即可控制电磁微锻机构的锤击频率和锤击能量。利用激光位移传感器测量电磁微锻机构冲杆底部凸台的位移，即可获得冲杆的实际位移。

电磁微锻机构的冲杆在运动过程中主要受到6个作用力，分别为安培力（即驱动力）、摩擦力、回弹力、冲击力、静磁力和重力，其关系如下：

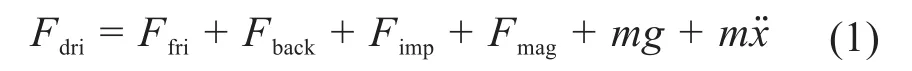
式中：Fdri为驱动力，Fdri=i(t)Bl0，其中i(t)为线圈瞬时电流，B为磁感应强度，l0为线圈绕组长度；Ffri为摩擦力；Fback、Fimp分别为回弹力和冲击力，其与冲杆、机构的上限位和工件的材料特性相关；Fmag为静磁力；m为冲杆的质量；x¨为冲杆的加速度。

从能量角度分析，驱动力功率Wdri的一部分用于改变冲杆的动能和重力势能，其与冲杆的重力和加速度有关，在冲杆运动的一个周期内保持不变，另一部分转化为冲击损耗Wimp、和摩擦损耗Wfri，其与机构的机械结构、机构和工件的材料特性和冲杆运动速度有关，通常情况下冲杆运动速度越大，冲击损耗和摩擦损耗越大。由此可知，在冲杆运动的一个周期内，驱动力功率与冲击损耗和摩擦损耗的关系如下：

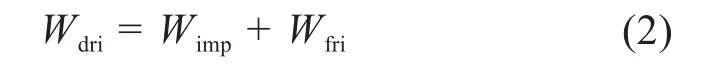
电磁微锻机构中线圈的输入电压、电感电压、绕组电压以及反电动势满足回路电压定律：

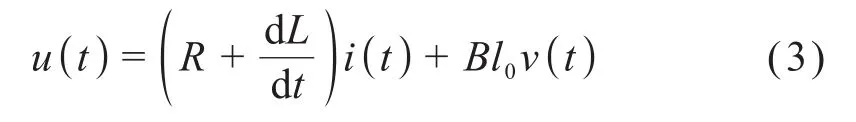
式中：u(t)为线圈的瞬时输入电压；R为线圈电阻；L为线圈电感；ν(t)为冲杆的瞬时速度。

在式（3）等号两边同时乘以i(t)，可得：

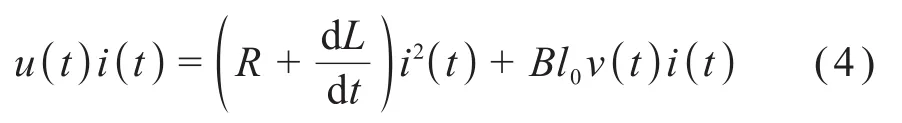
由式（4）可知，输入功率Win=u(t)i(t)一部分用于改变电感能量dLi2（t）/dt，其中电感能量分为磁轭的铁芯损耗Wiron和电感储能，电感储能在一个工作周期内不变；另一部分转化为驱动力功率Wdri=Bl0ν（t）i（t）和线圈损耗Wcoil=i2（t）R，即有：

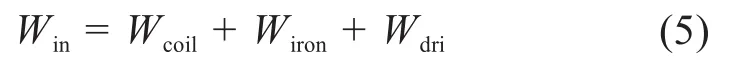
由此可知，电磁微锻机构的输入功率主要转换为四部分功率损耗，分别为线圈损耗、铁芯损耗、冲击损耗和摩擦损耗，可表示为：

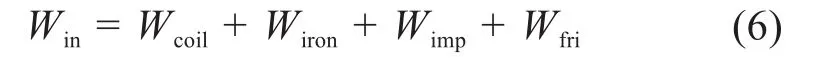
冲击损耗Wimp和摩擦损耗Wfri为冲杆作直线往复运动时所消耗的能量，当冲杆的运动状态及工件的材料不变时，冲击损耗Wimp、摩擦损耗Wfri不发生变化；铁芯损耗Wiron为磁轭铁芯涡流产生的焦耳热，线圈损耗Wcoil为线圈产生的焦耳热。其中，冲击损耗Wimp为能量转换过程中的有用功，则定义能量转换效率η为：

在能量转换效率一定的情况下，电磁微锻机构冲杆对工件冲击所能达到的最大功率与线圈损耗、铁芯损耗等内部损耗成正比，但内部损耗过大会导致微锻机构部分构件过热。由此说明，热效应会限制电磁微锻机构冲击时所能达到的最大输出功率。

2 电磁微锻机构温度场仿真分析

为研究热效应在电磁微锻机构内部的表现形式，对其内部温度场进行仿真分析。本文所研究的电磁微锻机构采用强制风冷和水冷相结合的冷却方式。冷却空气由储气罐提供，经由微锻机构上部腔体、铁芯，穿过线圈绕组和永磁体，最终从机构底部的气孔散出；冷却水由冷水机提供，经过内部的水冷头和线圈骨架进行换热。图2所示为电磁微锻机构的冷却结构示意图。

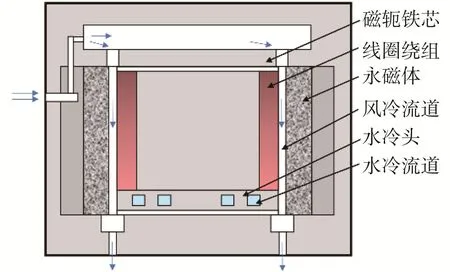
图2 电磁微锻机构冷却结构示意Fig.2 Schematic diagram of cooling structure of electromagnetic micro hammer peening mechanism

由于电磁微锻机构的结构新颖且设计复杂，其内部流道的布置与传统的换能装置（如电机、变压器等）有很大的差别，采用经验公式计算电磁微锻机构内部气体及液体与流道壁面的对流换热系数难以得到较为精确的值。

CFD（computational fluid dynamics，计算流体力学）是通过使用数值分析和结构化的数据来计算和解决流体流动所涉及的问题，以模拟流体的自由流动以及在一定边界条件下流体与流道表面之间的相互作用。本文采用的CFD仿真模型为共轭传热模型，即：将固体传热与层流或湍流流体中的传热相耦合，并设置压力、速度、温度和通量等边界条件，求解流体的速度、压力以及流体和固体的温度，从而得到较为准确的温度场。然后，根据CFD仿真计算结果，采用等效对流换热系数来表示流体（气体和液体）与流道壁面的换热作用，从而对电磁微锻机构内部的瞬态温度场进行计算，以及研究不同加载条件和冷却方式下微锻机构的温升情况及温度分布。

2.1 风冷和水冷方式下温度场CFD仿真分析

使用COMSOL Multiphysics软件中CFD模块的yPlus代数湍流模型对风冷和水冷方式下电磁微锻机构内部流道的对流换热情况进行仿真计算。为了提升计算效率，对仿真模型进行简化处理：

1）设置紧固件与零部件之间紧密贴合，接触热阻为0 K/W，材料相同；

2）在分析气体与流道壁面的对流换热系数时，忽略液体与流道的换热，即假设2种换热过程之间互不影响，计算液体与流道壁面的对流换热系数时作相同处理；

3）机构壳体外侧的热传递形式设为自然对流换热及表面辐射换热形式；

4）内部流道形状对求解过程中的因变量（如压力、速度）的影响较大，须按照原有的形状进行计算；

5）根据气体入口压力的测量结果，将入口处边界条件设定为压力边界条件；

6）电磁场与温度场之间的耦合方式选择单向耦合，即假定电磁场引起的损耗特性不随温度变化。

基于上述假设，分别对风冷和水冷方式下电磁微锻机构内部流体的流线速度及其温度分布进行CFD仿真分析。图3所示为风冷方式下入口压力为0.2 MPa、线圈热功率为40 W时电磁微锻机构内部气体的流线速度分布以及气体和风冷流道的温度分布；图4所示为水冷方式下入口流速为0.5 m/s、线圈热功率为40 W时液体的流线速度分布以及液体和水冷头固接部分的温度分布。

由图3可以看出，风冷流道的入口处较长且较窄，由于存在壁面阻力，使得压头损失很大。同时，在电磁微锻机构上部腔体内，风冷流道突然扩大，气体离开较窄的流道壁面后形成射流注入到扩大的流道，并逐渐扩大到整个截面，使得流速减小，压力增大，从而在射流和流道壁面之间产生旋涡，消耗机械能。基于此，在后续的结构优化中，可对风冷流道入口狭窄和口径变化过大的问题进行改进。

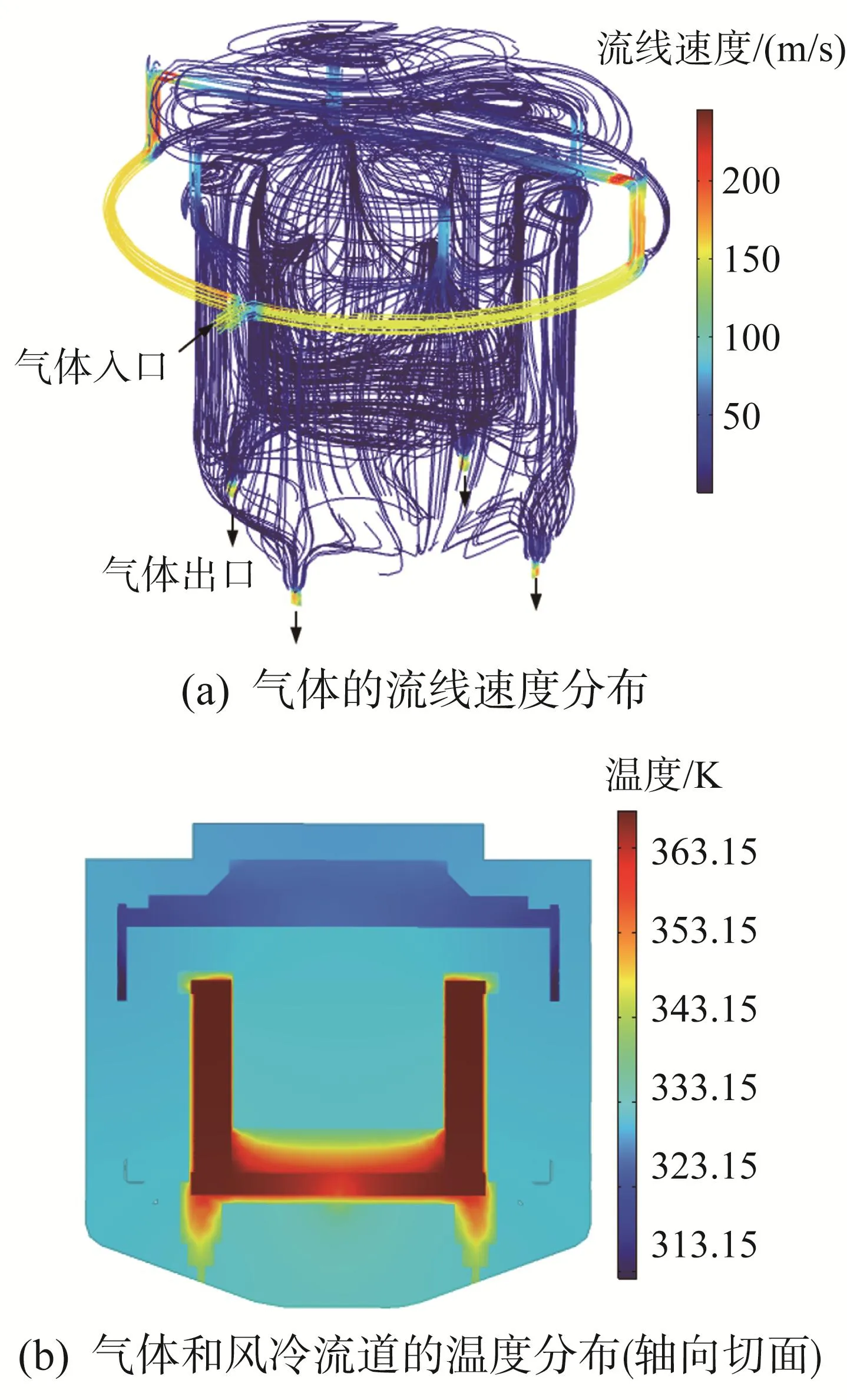
图3 风冷方式下电磁微锻机构的CFD仿真分析结果Fig.3 CFD simulation analysis results of electromagnetic micro hammer peening mechanism under air-cooling mode

由图4可以看出，水冷头固接部分温度梯度较大处主要集中在线圈骨架处，这是由水冷头固定在线圈骨架顶部所造成的。基于此，后续可对线圈骨架的结构进行改进，如将水冷流道置于线圈骨架内部，以增大换热效率。

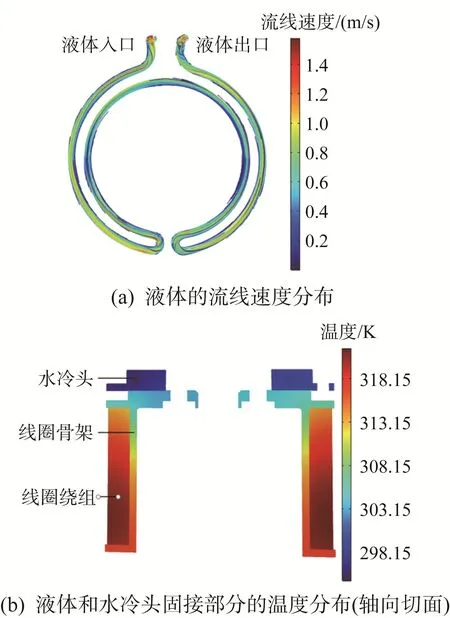
图4 水冷方式下电磁微锻机构的CFD仿真分析结果Fig.4 CFD simulation analysis results of electromagnetic micro hammer peening mechanism under water-cooling mode

2.2 等效对流换热系数确定

尽管通过CFD仿真分析可以准确地计算气体和液体的流速分布及温度分布，但是CFD仿真分析的计算效率较低。因此，采用计算量较小的对流换热系数来表征流体与流道壁面的换热作用，并研究线圈热功率、入口压力和入口流速与对流换热系数之间的关系。

采用稳态固体传热模型，将空气与永磁体内壁及线圈绕组的对流换热、水流与水冷头的对流换热用等效的壁面对流换热系数来表示。分别计算线圈在稳态固体传热模型和CFD仿真模型中的平均温度，使2种方法所得的线圈平均温度相等，从而获得等效对流换热系数。

根据上文构建的风冷方式下的CFD仿真模型，设定入口温度为293.15 K。在分析线圈热功率对等效对流换热系数的影响时，控制入口压力恒定为0.2 MPa，线圈热功率为5～50 W，间隔5 W；在分析入口压力对等效对流换热系数的影响时，控制线圈热功率恒定为40 W，入口压力为0.2～0.7 MPa，间隔0.1 MPa。对风冷流道的对流换热情况进行CFD仿真分析，整合得到的等效对流换热系数与线圈热功率、入口压力之间的关系如图5所示。

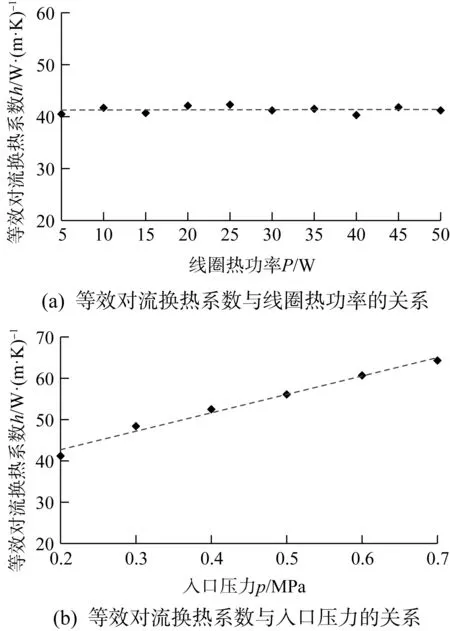
图5 风冷方式下等效对流换热系数与线圈热功率、入口压力的关系Fig.5 Relationship between equivalent convective heat transfer coefficient and coil thermal power，inlet pressure under air-cooling mode

利用线性相关系数r来衡量等效对流换热系数h与线圈热功率P、入口压力p之间的线性相关性。相关系数r的计算式如下：

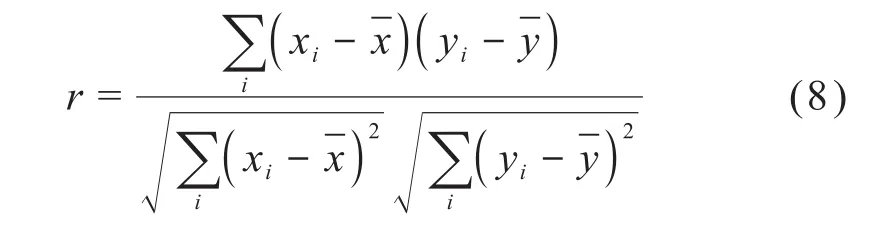
式中：xi、yi分别为变量x、y的第i个值；分别为变量x、y的平均值。

经计算，等效对流换热系数h与线圈热功率P之间的线性相关系数为0.05，该值较小，说明h与P之间几乎没有线性关系。同理，对等效对流换热系数h与入口压力p进行相关性分析，其线性相关系数为0.99，由此可知h与p之间基本呈线性关系，拟合可得：

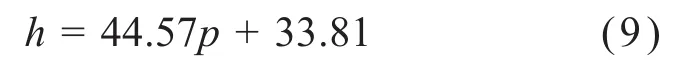
使用同样的方法分析水冷方式下等效对流换热系数与线圈热功率、入口流速间的关系。基于上文构建的水冷方式下的CFD仿真模型，设入口温度为293.15 K。在分析线圈热功率对等效对流换热系数的影响时，控制入口流速恒定为0.5 m/s，线圈热功率为5～50 W；在分析入口流速对等效对流换热系数的影响时，控制线圈热功率恒定为40 W，入口流速为0.1～1.0 m/s。对水冷流道的对流换热情况进行CFD仿真分析，得到的结果如图6所示。经计算得，水冷方式下等效对流换热系数与线圈热功率、入口流速的线性相关系数分别为0.22和1.00。由此可知，水冷方式下等效对流换热系数与入口流速之间基本呈线性关系，拟合可得：

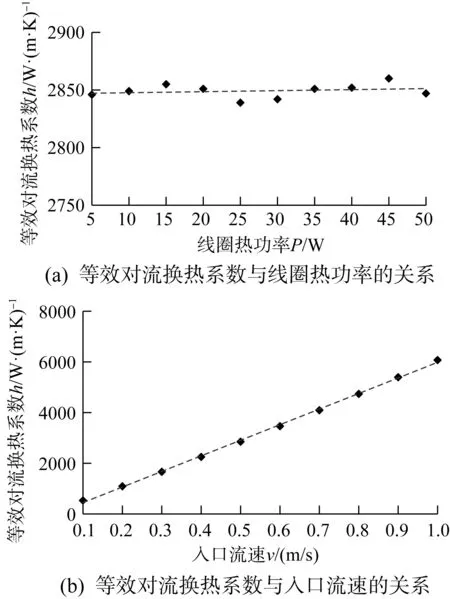
图6 水冷方式下等效对流换热系数与线圈热功率、入口流速的关系Fig.6 Relationship between equivalent convective heat transfer coefficient and coil thermal power，inlet velocity under water-cooling mode

2.3 瞬态温度分析模型建立

微锻加工过程一般是连续的，为了测量线圈的平均温度，须暂停通入交流信号并通入直流信号，但这会对加工过程产生影响。因此，基于上文计算所得的等效对流换热系数，构建瞬态温度分析模型，以预测电磁微锻机构各构件在不同加载条件及冷却方式下的温度变化情况。

本文所采用的风冷系统由压缩机、储气罐、输送管路和电磁微锻机构内部的风冷流道组成，到达电磁微锻机构的冷却空气的压力由储气罐压力、输送管路长度和风冷流道结构共同确定。储气罐的出口气压稳定在0.60～0.70 MPa。由于硅胶软管较长，空气在软管内会有一定的压力损失，同时电磁微锻机构风冷流道的结构较为复杂，不能直接将储气罐的出口气压作为风冷流道的入口压力。因此，使用皮托管测量电磁微锻机构风冷流道的入口静压，作为计算等效对流换热系数的入口压力。测量结果为0.62～0.66 MPa，取平均值0.64 MPa，则风冷方式下对应的等效对流换热系数h≈62.33 W/(m2·K)。水冷流道的冷却水由冷水机提供，使用调速泵控制水冷流道入口流速，令入口流速为0.8 m/s，则水冷方式下对应的等效对流换热系数h≈4 753.6 W/(m2·K)。

基于COMSOLMultiphysics软件中的固体传热分析模块，将电磁微锻机构模型简化后并导入，设定各构件的材料及其导热系数，如表1所示。对于所有接触表面，使用间隙气体的收缩热导率模型计算其热阻。

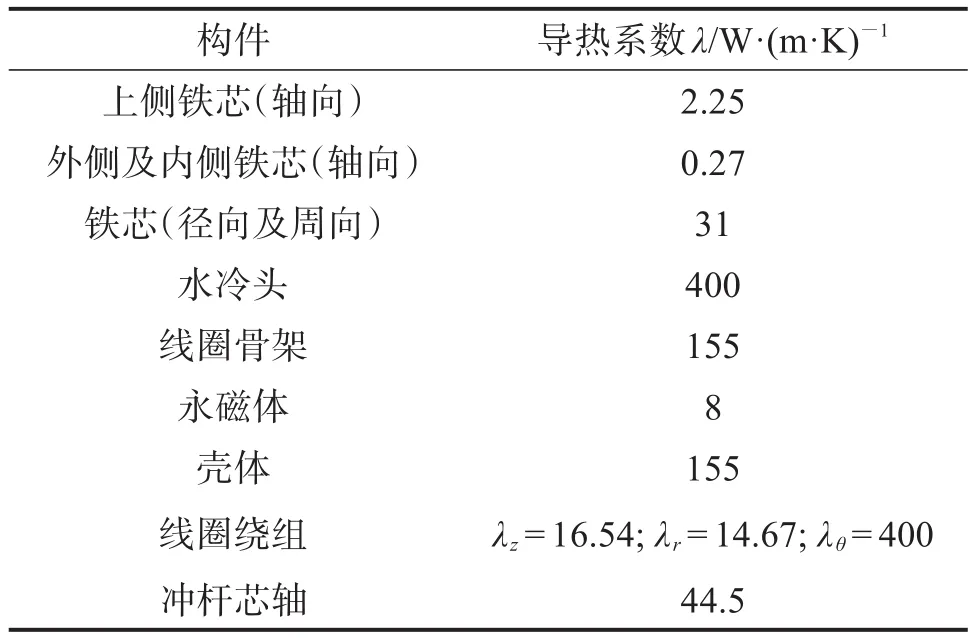
表1 电磁微锻机构各构件的导热系数Table 1 Thermal conductivity of each component of electromagnetic micro hammer peening mechanism

电磁微锻机构外表面的自然对流换热系数包含以下无量纲数：格拉晓夫数Gr、普朗特数Pr、努塞尔数Nu和瑞利数Ra。对于特征长度为L的垂直面、水平平板上侧以及水平平板下侧，确定努塞尔数Nu和瑞利数Ra的系数C和n的经验公式不同，因此应根据电磁微锻机构外表面的形状选择不同的经验公式进行计算。

电磁微锻机构中磁轭铁芯的涡流损耗与线圈电流及输入电压的频率有关。在均匀材料、均匀磁场和无集肤效应的情况下，可根据式（11）计算单位质量薄片或金属丝的涡流造成的功率损失［13］：

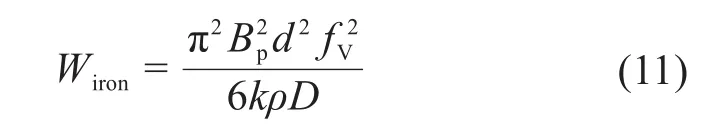
式中：Bp为峰值磁场；d为薄片或金属丝的厚度；fV为输入电压的频率；k为常数，对于薄片而言，k=1；ρ为材料的电阻率；D为材料的密度。

磁轭铁芯由1 mm厚的硅钢片堆叠制成，而硅钢片可以看作薄片。根据实验数据，当输入电流有效值约为8.9 A，输入电压的频率为100 Hz、冲程为1 mm时，线圈热功率约为80 W，此时铁芯损耗约为0.2 W。冲杆和机构壳体通过直线轴承连接，根据摩擦热功率计算式Wfri=ffriν冲，以及冲杆的平均速度ν冲=0.2 m/s，经测量可得冲杆轴向运动时的摩擦力为3.5 N，总功率约为0.7 W。基于此，设线圈、铁芯和轴承的热功率分别为80，0.2和0.7 W。设置时间步长为5 s，总仿真时长为1 000 s，对上述条件下的电磁微锻机构进行瞬态温度场仿真分析，结果如图7所示。由图7可以看出，电磁微锻机构内部热量以线圈为中心向周围传递；线圈的温度远高于其余构件的温度，因此失效首先发生在线圈内部。

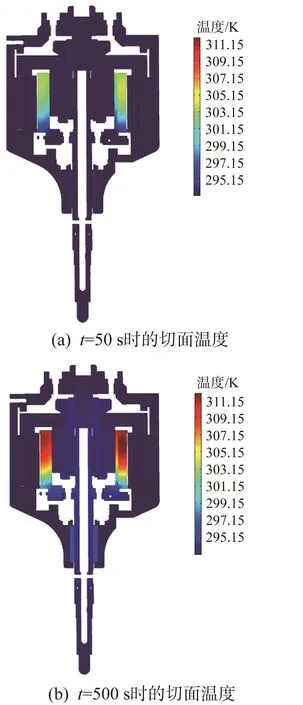
图7 电磁微锻机构瞬态温度场仿真结果Fig.7 Simulation results of transient temperature field of electromagnetic micro hammer peening mechanism

由图7还可以看出，线圈内部温度分布并不均匀，其平均温度和最高温度之间存在一定的差异，这是由电磁微锻机构的结构设计所导致的。经过多次瞬态温度场仿真分析，通过观察当线圈温度达到稳态时其平均温度和最高温度的差值，可得温差系数经验公式：

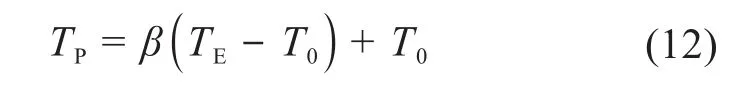
式中：TP为线圈的最高温度；TE为线圈的平均温度；T0为环境温度；β为温差系数，在风冷方式下β=1.06，在水冷和风冷相结合方式下β=1.19。

以A级绝缘为例，线圈最高温度不应超过378.15 K，根据式（12）计算得到线圈的平均温度不应超过359.85 K，此时对应的线圈热功率为290 W。

3 温升特性及稳态温度特性实验研究

上文基于CFD仿真模型从理论上分析了风冷和水冷方式下的等效对流换热系数，并得到了瞬态温度分析模型，同时计算了线圈的温度分布和温升特性。现通过实验来验证上述结果的准确性。将电磁微锻机构固定在三自由度平台上，利用其对固定在工作台上的长方体TC4材料进行单点冲击并测量线圈的温度，实验平台如图8所示。

图8 电磁微锻机构温度测量实验平台Fig.8 Experimental platform for temperature measurement of electromagnetic micro hammer peening mechanism

使用间接法测量电磁微锻机构线圈的温度。其中线圈电阻率随温度的关系、线圈的平均温度以及线圈电阻与电阻率的关系分别为：

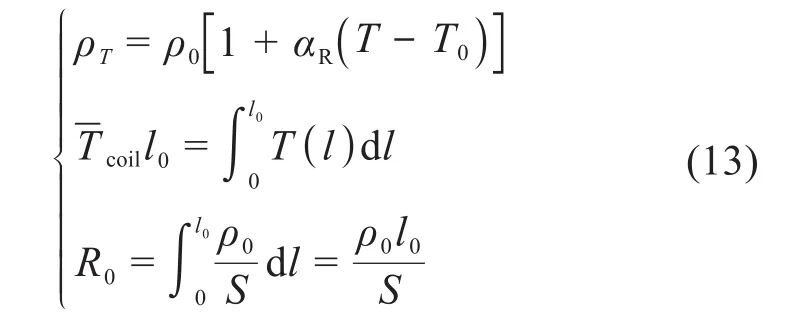
式中：ρT为温度T时线圈的电阻率；ρ0为室温下线圈的电阻率；αR为线圈的电阻温度系数；T0为室温；为线圈的平均温度；R0为室温下线圈的电阻；S为线圈截面面积。

根据式（13）可以推导出线圈电阻与线圈平均温度的关系：

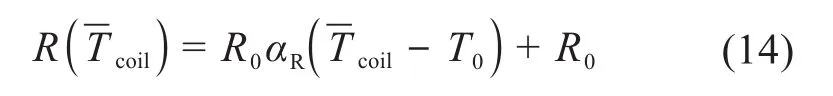
则线圈的平均温度可以表示为：

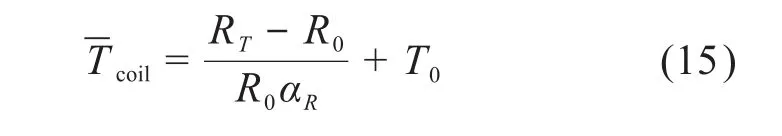
式中：RT为温度T时线圈的电阻。

使用IT7600系列交流可编程电源对电磁微锻机构进行控制并测量其线圈的电阻，搭建Winform窗体应用程序，调用NI（national instruments，国家仪器）控制接口，通过 SCPI（standard commands for programmable instruments，可编程仪器标准命令）进行数据接收和控制。输入的电压信号如图9所示，通入19 s交流信号以输入功率，随后通入1 s直流信号以测量线圈电阻，周期性反复循环。在温升特性验证实验中，维持80 W的线圈热功率，输入交流信号及直流信号1 000 s，记录当前时刻线圈的平均电阻，用于计算线圈的平均温度，并与仿真计算结果进行对比。微锻电磁机构线圈的温升特性曲线如图10（a）所示。在稳态温度特性验证实验中，记录线圈热功率为30～150 W时线圈的稳态温度，结果如图10（b）所示。

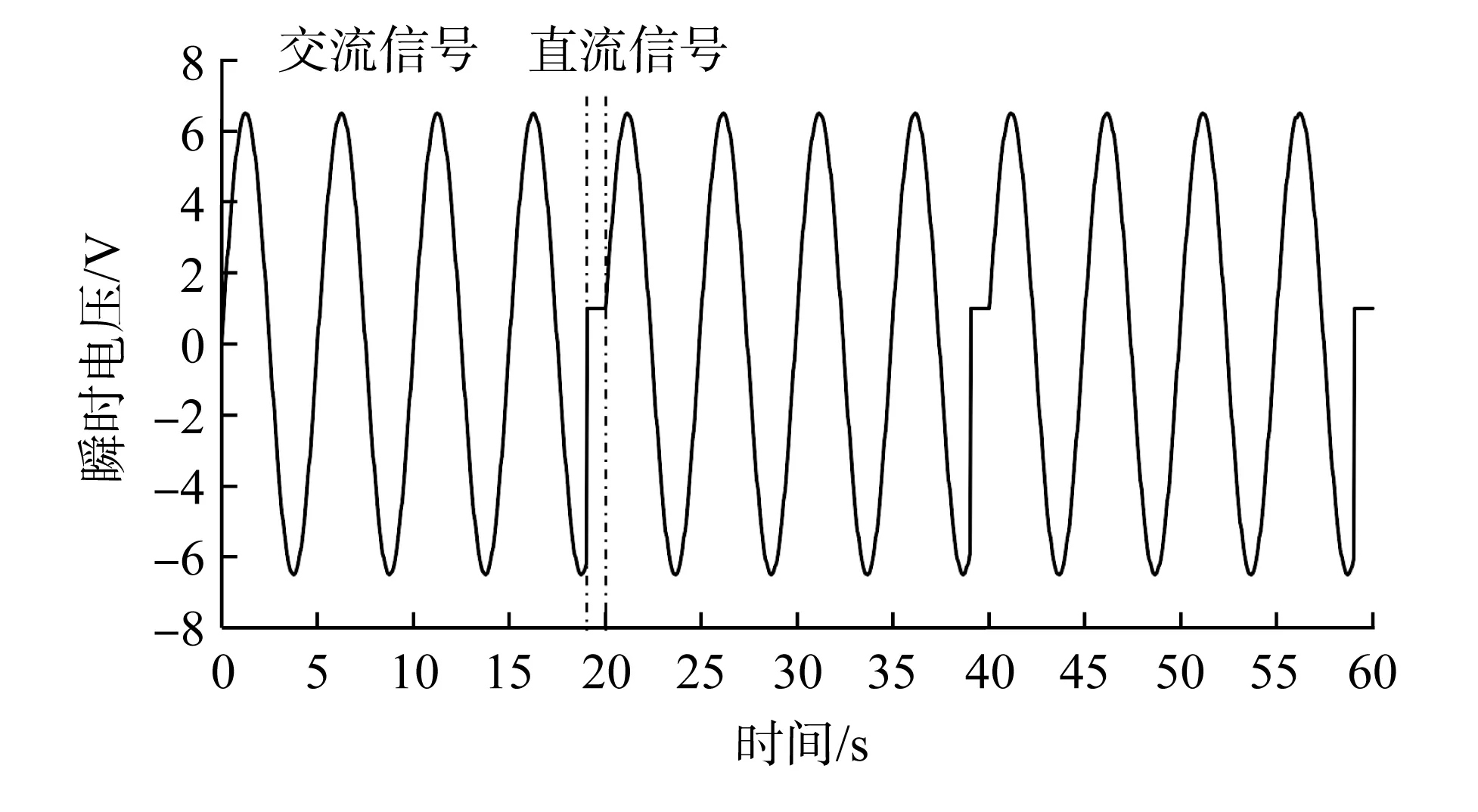
图9 电磁微锻机构的输入电压信号示意Fig.9 Schematic diagram of input voltage signal of electromagnetic micro hammer peening mechanism

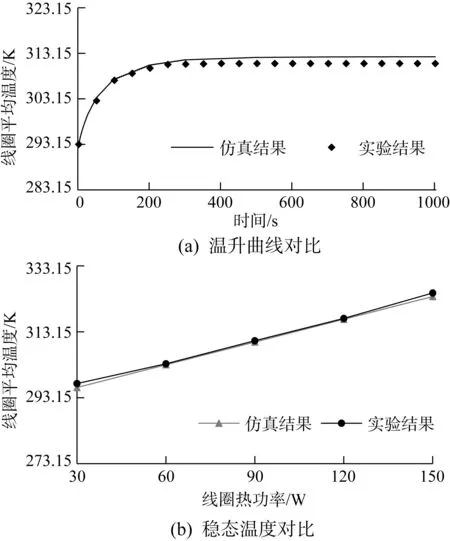
图10 电磁微锻机构线圈的温升曲线及稳态温度对比Fig.10 Comparison of temperature rise curve and steadystate temperature of coil of electromagnetic micro hammer peening mechanism

对比电磁微锻机构线圈温升曲线的实验结果和仿真结果可知，线圈稳态温度实验值约为310.85 K，稳态时间实验值为360 s；稳态温度仿真值为312.45 K，稳态时间仿真值为350 s。以实验结果为基准，相对于室温，稳态温度的相对误差为8.2%，稳态时间的相对误差为2.7%。对比稳态温度实验结果和仿真结果可知，线圈平均温度实验结果与仿真结果的平均误差为0.43 K，最大误差为1.2 K。鉴于仿真分析过程包含等效处理和简化处理，误差基本在合理范围内，由此说明本文所构建的电磁微锻机构瞬态温度分析模型较为合理。