基于 GBDT 的铁路事故类型预测及成因分析

钟敏慧 张婉露 李有儒 朱振峰 赵 耀

近年来,我国铁路事业高速发展,在推动国民经济发展中发挥着至关重要的作用.与此同时,铁路安全问题也愈发受到重视.在大数据时代,如何利用铁路事故历史记录数据发掘有用信息,建立事故预警机制,对于推动铁路行业信息化,提高运输效率,防范安全隐患具有重要意义.铁路事故类型预测和事故致因分析是建立事故预警机制的两个基础环节.铁路事故预测利用历史事故记录估计和判断未来某种情况下是否会发生事故.铁路事故成因分析通过分析事故发生时的客观环境与人为因素,寻找造成事故的最可能原因,从而采取针对性的预警防护手段.因此,利用铁路事故历史记录,采用数据挖掘技术发掘其中有用信息,进行铁路事故类型预测与成因分析具有重大现实意义.

铁路事故类型预测的本质是一个多分类问题.常用的多分类模型有逻辑回归(Logistic regression,LR)[1]、支持向量机(Support vector machine,SVM)[2]和决策树(Decision tree,DT)[3]等.文献[4]利用决策树算法进行煤与瓦斯的突出预测.然而,这类分类器主要适用于简单、平衡的数据训练,对于铁路事故记录这种复杂、类别失衡的高维数据,训练较为困难,且预测结果不够理想.集成学习能够将多个模型集成以获取更好的预测结果,对于不平衡数据的分类问题具有更好的有效性.常用集成学习模型主要包括随机森林(Random forest,RF)[5]和梯度提升决策树(Gradient boosting decision tree,GBDT)[6-7].RF 基于Bagging 思想[8],并行集成基学习器,模型简单,计算开销小;而GBDT 则是基于Gradient boosting 思想[6,9],对基学习器进行串行集成,对数据拟合能力很强.文献[10-13]分别使用以上模型进行预测.

铁路事故成因分析是对事故类型预测的反演.常用的事故成因分析方法有复杂网络方法、灰色理论等.文献[14]结合灰色综合关联度和信息熵,利用熵分析事件不确定性的原理,针对事故相关属性的重要度进行分析.文献[15]运用多维关联规则提取技术找出事故成因关联规则.上述事故成因分析方法对于值类别数较多的特征,运算较复杂.

此外,现有铁路事故记录数据存在严重的数据缺失问题,在进行铁路事故类型预测和归因前,首先需要对数据进行补全.选择合适的补全方法对于提升预测结果的准确性有很大影响.目前,常用的补全方法主要包括均值填补法、最近距离填补法、回归填补法等[16-17].然而,前两种方法在某种程度上会影响样本状态分布,导致预测结果的偏差;回归填补法仅适用于连续特征,对于离散特征并不适用.

针对上述问题,本文提出了一种基于GBDT的铁路事故类型预测及成因分析算法.首先,针对铁路事故数据缺失问题,提出了一种基于属性分布概率的补全算法,该算法最大程度地保持了原有的数据结构,从而降低数据缺失对于类型预测造成的影响.其次,提出了一种基于Bagging 的集成GBDT模型,针对类别失衡的铁路事故历史记录数据能够进行高效训练,得到准确的事故类型预测结果.同时,结合统计学习理论,根据GBDT 预测模型中的特征重要度排序,实现事故致因分析.算法整体框架如图1 所示.通过在公开的铁路事故数据库上进行实验,验证了本文所提算法的有效性.

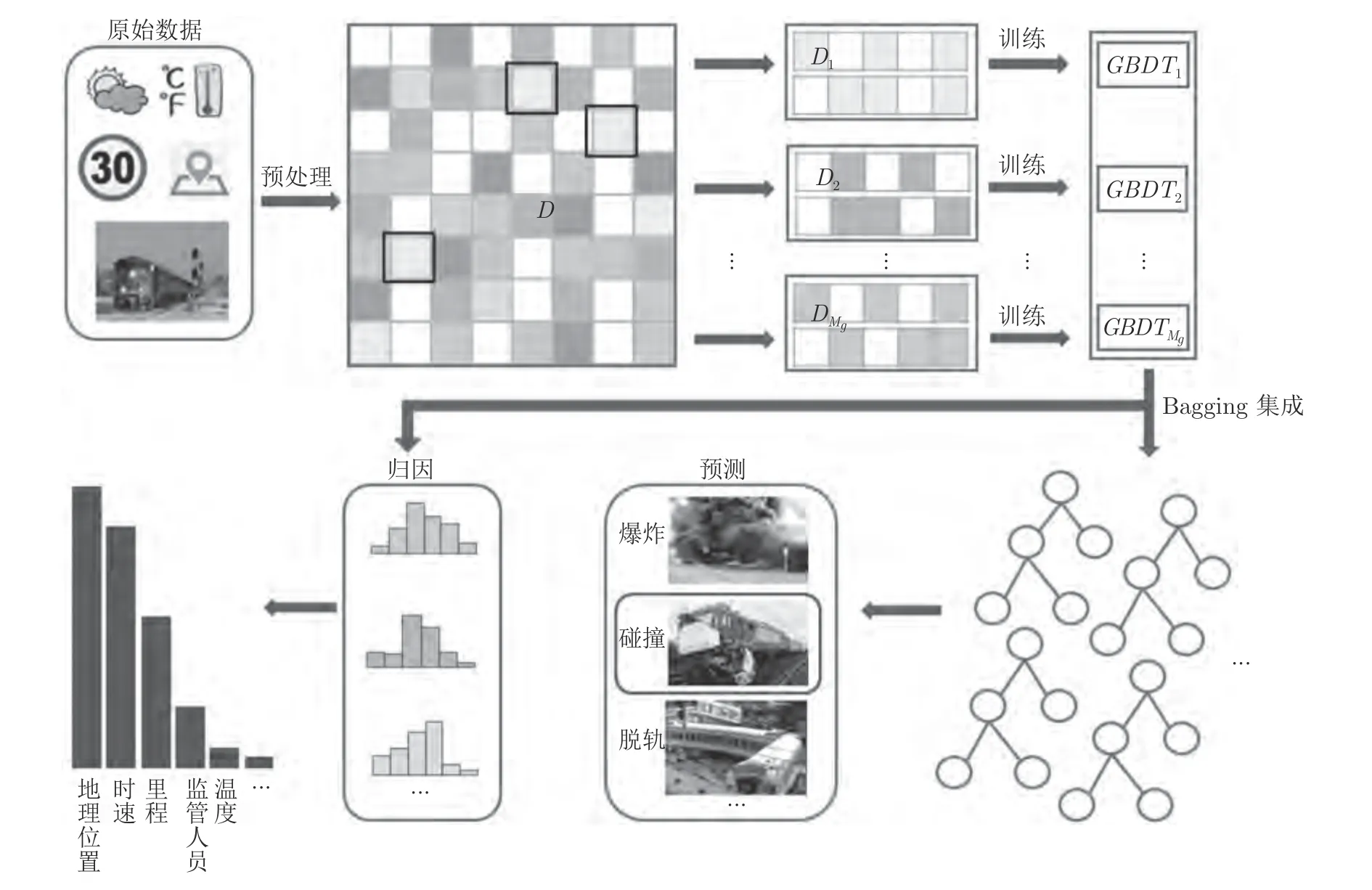
图1 基于GBDT 的铁路事故类型预测及成因分析框架Fig.1 The framework of GBDT-based railroad accident type prediction and cause analysis

1 铁路事故缺失数据补全算法

在本节中,我们主要介绍本文所提出的基于属性分布概率的缺失数据补全算法.其中,第1.1 节给出本文所用符号的说明.第1.2 节对算法进行具体描述.

1.1 符号说明

为便于后文阐述,首先对本文所用的一些符号进行说明.令D∈RN×(p+1)表示记录条数为N的铁路设备事故数据集,其中每条记录可表示为ddd=[XXXi,yi],0≤i ≤N.令X=[XXX1,XXX2,···,XXXN]T∈RN×p表示N条记录的p维特征空间,其中表示每一条记录的p维特征向量.Y=[y1,y2,···,yN]T∈RN×1表示N条事故记录的类型向量,其中,yi∈{1,···,C},C为事故类型总数量.令xj表示第j个特征,1≤j ≤p,使用aj表示xj的取值.若xj是离散的类别型属性,则类别aj∈{1,···,k},其中k为xj可取类别值的数量.

1.2 基于属性分布概率的补全算法

由于客观环境及人为原因等干扰因素,导致铁路事故记录数据存在缺失,对后续事故类型预测建模及成因分析有不利影响.因此,需对铁路事故数据进行缺失补全.

目前常用的补全方法包括均值补全、众数补全等.然而,由于铁路事故记录数据中的属性多为离散的类别型属性,常规补全方法并不适用.例如,均值补全适用于连续的数值型属性;众数补全适用于数据本身缺失较少,其中需补全的属性的取值分布有明显偏好的情况,对于取值分布较均衡的属性,使用众数补全会改变原有属性取值的概率分布.

考虑到上述问题,本文提出了一种基于属性分布概率的补全算法.算法流程由算法1 给出.针对铁路事故记录数据中取值分布较均衡的离散、类别型属性xj,计算现有数据下该属性所有取值aj=n出现的概率,基于概率进行缺失值的填补,从而在保持属性原有的分布的情况下,完成对铁路事故数据的补全,降低数据缺失对事故类型预测的影响.

计算公式如下:

2 铁路事故类型预测

铁路事故预测本质上是一个多分类问题.由于铁路事故记录数据类别不均衡且属性多为离散值属性,GBDT 在处理这类数据时具有很好的有效性.本章节详细介绍了基于改进GBDT 的铁路事故类型预测模型.其中,第2.1 节简要介绍了GBDT 模型,第2.2 节对本文所提模型进行详细阐述.

2.1 GBDT 模型

GBDT 是基于Boosting 算法[9]的集成决策树模型.Boosting 算法依据上一次训练的残差生成基学习器.GBDT 在Boosting 的基础上,在残差减小的梯度方向上建立新的决策树[6-7].GBDT 模型可表示为:

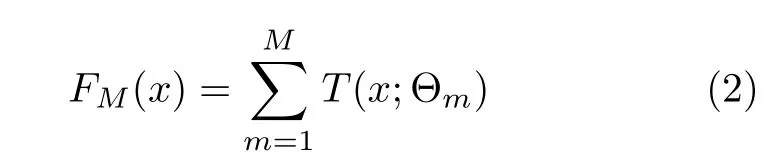
其中,T(x;Θm) 表示决策树,Θm表示树的参数,M为树的个数.

决策树T(x;Θm) 的损失函数用L(·) 表示,在GBDT 中,损失函数为平方误差函数.用Tm-1(x)表示当前决策树,GBDT 通过最小化损失函数来确定下一棵决策树的参数.

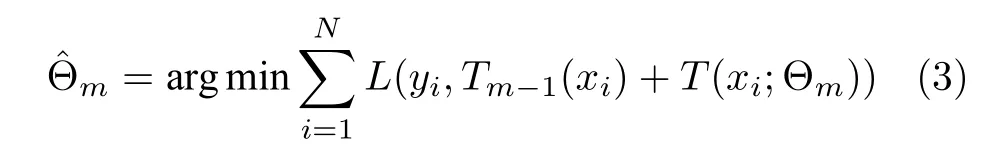
2.2 基于Bagging 的集成GBDT 模型

由于铁路事故样本存在类别失衡的问题,使用单一GBDT 难以满足分类需求.集成学习中的Bagging 算法能够随机有放回地选择训练数据,构建基学习器,然后将多个基学习器组合,使用投票法或简单平均法计算分类结果[8,18-19].文献[20]和[21]都是通过将多个分类器集成,以获得更好的分类效果.本文参考文献[20],提出一种基于Bagging 的集成GBDT 算法,以GBDT 作为基学习器,利用Bagging 算法将多个GBDT 集成,构造集成GBDT 模型,获得比单一GBDT 优越的分类效果,克服样本类别失衡对预测造成的影响,实现铁路事故类型的精确预测.

算法流程如算法2 所示.对于输入的训练集(X,y),利用Bootstrap 算法[8]以采样率α随机采样Mg次,得到Mg个训练子集,从而构造Mg个GBDTt,t=1,···,Mg;对于每一个GBDTt的预测值,利用投票法,选择Mg个GBDTt的预测结果中出现次数最多的预测值作为集成GBDT 的最终预测结果.

3 铁路事故致因分析

铁路事故致因分析是铁路事故类型预测的反演,通过对铁路事故发生时各种因素的分析,能够推演事故发生的过程和解析事故因果关系,以建立事故预警机制,进行安全防范.由于铁路事故记录数据特征维度较大,传统致因分析方法[14-15]并不适用.在进行GBDT 模型训练时,可以输出特征重要度,以分析哪些特征对预测结果存在关键影响.因此,本文结合统计分析的方法,基于GBDT 的特征重要度排序[6],进行铁路事故致因分析.

对于某一特征xj的全局重要度,通过该特征在单棵决策树中重要度的平均值来衡量,如式(4)所示.

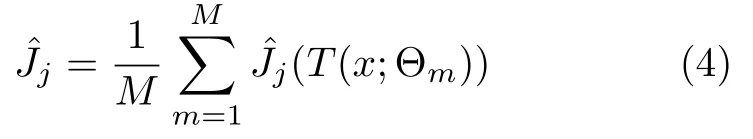
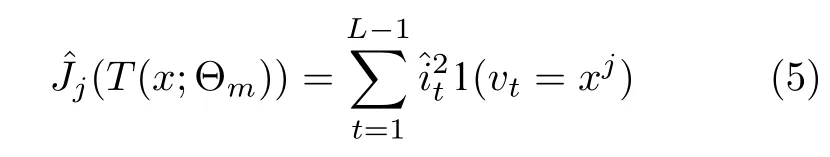
其中,L表示树的叶子节点数量,L-1 即为树的非叶子节点数量,vt表示与节点t相关联的特征,是节点t分裂之后的平方损失的减少值[6].

分析可得,非叶子节点t在分裂时的越大,说明特征越重要.根据重要度排序筛选出特征后,按排序将特征分组累加代入预测模型重新训练,以验证选择的可靠性.

4 实验结果及分析

4.1 实验数据设置及预处理

本文通过在美国联邦铁路管理局(Federal Railroad Administration,FRA)[22]公开的铁路设备事故数据上进行实验,验证了本文所提算法的有效性.

实验数据采用FRA 对外公布的2016 年至2018 年铁路设备事故数据.数据集包含事故类型、事故发生具体时间、地点、日期、铁路编号等信息.原始数据集统计信息见表1,共5 434 条记录,包含144 个属性和11 种事故类型.11 种事故类型描述如表2 所示,其中,类型1 (Derailment)记录数量最多,类型2 (Head on collision)、类型6 (Broken train collision)记录数量极少.

表1 原始数据描述Table 1 Description of original data

表2 事故类型描述Table 2 Description of accident types

原始数据存在严重属性缺失情况,如表3 所示.本文首先通过多次数据清洗,去除部分与实验结果无关性较强的属性,最终保留69 个属性.这69 个属性中,共有23 个属性存在缺失,缺失属性均为类别型属性.本文采用众数补全和第1.2 节基于属性分布概率的补全算法两种方法进行数据补全.统计每一个缺失属性取值的概率分布,针对缺失属性类别分布较均衡的属性,使用本文所提算法进行补全;对于缺失值较少或类别分布有明显偏好的属性,采用众数补全.针对补全后的数据,对类别型属性进行编码，为后续模型训练做准备.经过预处理后数据集的统计信息描述如表4 所示.

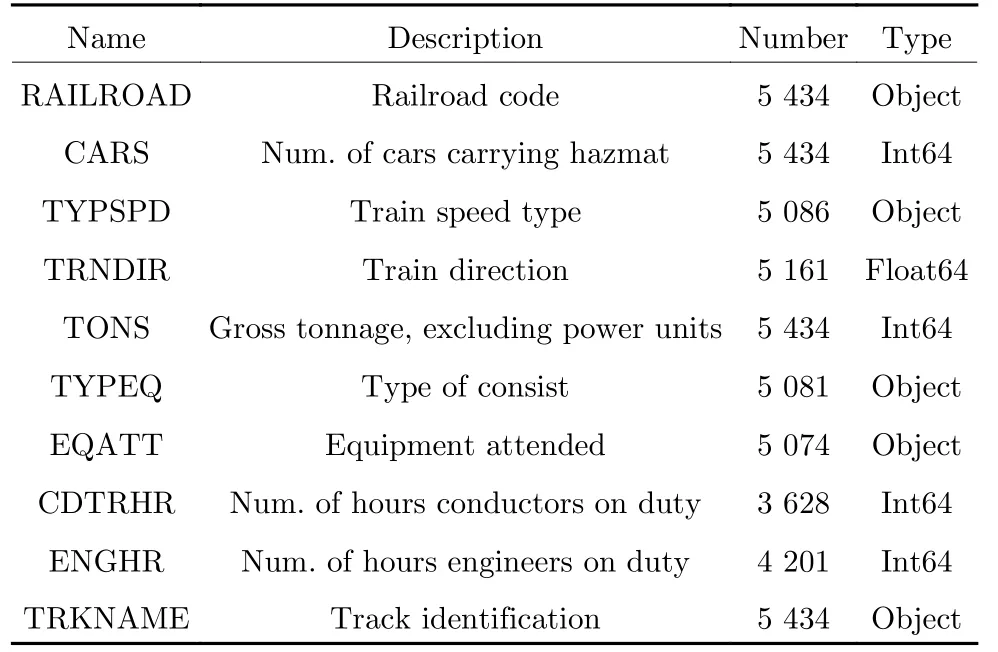
表3 数据集部分示例Table 3 Examples of the dataset

表4 预处理后数据描述Table 4 Description of preprocessed data

本文采用交叉验证的方式,随机选择80 %作为训练集,20 %作为测试集.

4.2 度量标准

本文通过在美国联邦铁路管理局(Federal Railroad Administration,FRA)[22]公开的铁路设备事故数据上进行实验,验证了本文所提算法的有效性.本文采用均方误差函数(Mean square error,MSE) 作为补全算法有效性的评价标准,其定义如下:

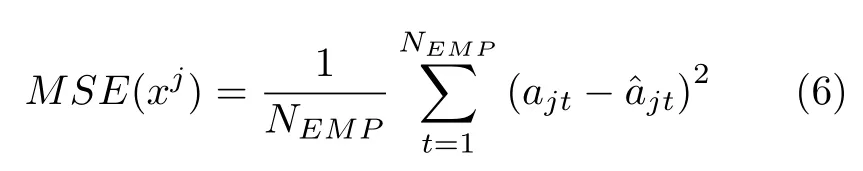
其中,NEMP表示手动设置的空值的总数,ajt表示原始值,表示插补后的值.

对于铁路事故类型预测模型,本文采用准确率Accuracy、查准率Precision、查全率Recall和F1-score 作为评价指标.

分类准确率计算公式为:

其中,C表示所有事故类型的总数;Ni表示事故类型为i的样本个数,N表示样本总个数;TPi表示被正确预测为第i类的个数;TNi表示被正确预测不为第i类的个数;FPi表示被错误预测为第i类的个数;FNi表示被错误预测为不为第i类的个数.

4.3 补全算法对比实验结果及分析

为验证基于属性分布概率的补全算法的有效性,本文将所提算法与插值法(Interpolation completer)、众数补全(Mode completer)两种补全方法进行比较.基于属性分布概率的补全算法最大程度地保持了原始数据的分布结构.以特征TRNDIR为例.特征TRNDIR 有4 种取值,aj∈{1,2,3,4}表示火车运行的四个方向.表5 展示了使用三种方法进行补全后与补全之前4 种取值的概率分布.从表5 可以看出,使用插值法与众数补全法补全后,造成该特征某一取值过多,破坏了原本的数据分布,而本文所提算法完全不改变原有的概率分布,从而减少了由于数据缺失对铁路事故类型预测带来的影响.

为进一步定量分析基于属性分布概率的补全算法的有效性,本实验以均方误差函数(MSE)作为评价标准,对3 种补全方法进行对比.以TRNDIR、ENGHR、CDTRHR (特征描述见表3)三个特征为例,随机从数据集中选择100 条记录,设置以上三个特征的值为空,用三种补全算法依次进行补全,记录每一种补全算法MSE.共进行10 次实验,取10 次MSE 之和的平均值进行对比,实验结果如图2所示.由图2 可得,基于属性分布概率的补全算法MSE 明显低于其他两种方法,表明本文所提算法具有很好的有效性.

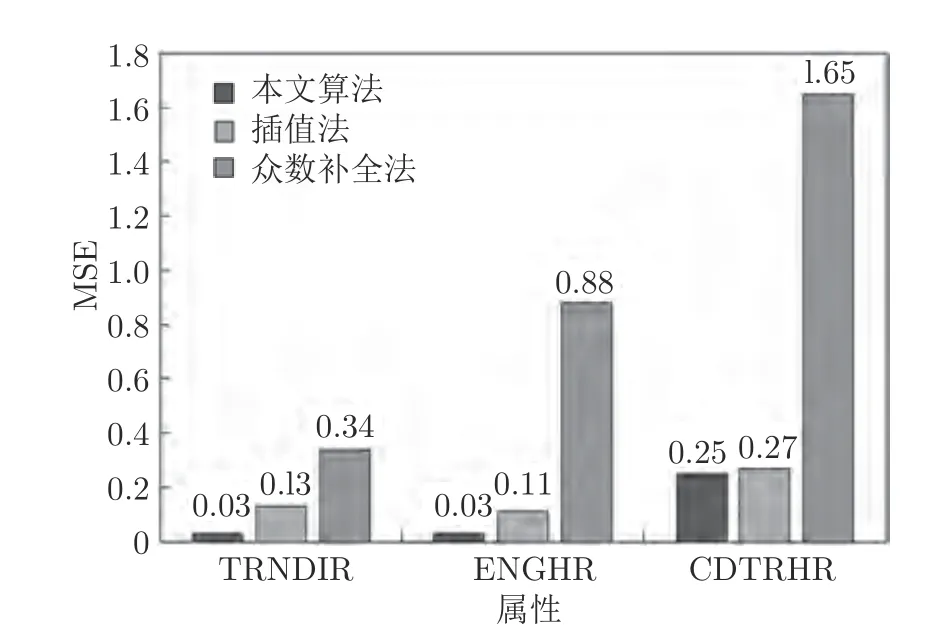
图2 三种补全方法结果对比Fig.2 Comparison of three methods results

4.4 模型集成实验结果及分析

为验证构造基于Bagging 的集成GBDT 模型时不同因素的影响,本节对不同参数下集成GBDT 的效果进行了对比,以确定进行铁路事故类型预测任务时的最佳参数设置.

基于Bagging 的集成GBDT 模型需要调优的参数可分为两类,包括Bagging 框架参数和GBDT 参数,GBDT 参数又包括Boosting 框架参数和决策树参数.其中,Bagging 框架参数包括最大迭代次数,即集成的GBDT 数量,以及最大采样率;Boosting 框架参数包括最大迭代次数,即子树的最大数量,以及学习步长等;决策树的参数主要包括树的深度.

首先,利用网格搜索法对单一GBDT 的参数进行调优.经过调优后,GBDT 的迭代次数为100,学习步长为0.2,决策树最大深度为6.此时GBDT 在测试集上的预测准确率为84.1 %.

得到最优GBDT 参数组合后,对集成GBDT的Bagging 框架参数进行调优,考虑运行效率和分类性能,以选择合适的GBDT 数量及采样率.在实验中,首先确定GBDT 个数,分别用5、10、15、20、25、30 个GBDT 进行集成,此时最大采样率设置为0.9,以在测试集上预测结果的准确率和模型训练时间作为评价标准,结果如图3 所示.数量为1时表示不进行集成,仅用单一GBDT 进行预测.可以看出,当GBDT 个数增加时,模型预测准确率呈上升趋势,表明使用Bagging 进行集成的方法确实有效.当GBDT 个数为15和25 时,模型预测准确率最高,达到85 %～ 85.2 %,比单一GBDT 预测准确率高出约1 个百分比,但使用15 个GBDT 训练的时间是使用25 个GBDT 训练时间的1/2.综合考虑分类效果和性能,最终预测模型使用15 个GBDT 进行集成.为进一步确定采样率,分别将采样率设置为0.6、0.7、0.8、0.9、1.0 进行实验,GBDT的数量设置为15,以预测结果的准确率作为评价标准.最终结果如表6 所示.可以看出,当采样率为0.9 时,模型预测准确率最高.

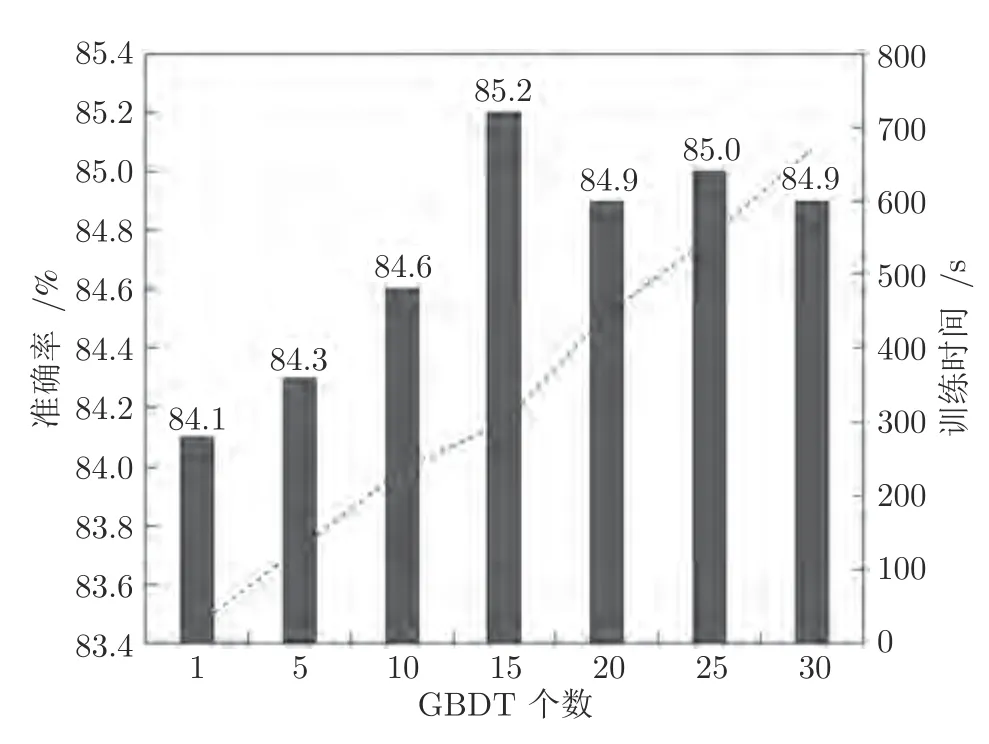
图3 不同GBDT 集成个数下分类准确率Fig.3 Accuracy of classifiers with different number of GBDT

表6 不同采样率下集成GBDT 分类准确率Table 6 Accuracy of classifiers with different sampling rates

4.5 模型选择实验结果及分析

为进一步验证基于Bagging 的集成GBDT 模型的有效性,本实验中使用相同的训练集,分别对DT[3]、RF[5]、ET[8]、GBDT[6-7]和集成GBDT (Ensemble GBDT)进行训练,在相同测试集上进行测试,对比预测结果.共进行10 次实验,取10 次结果的平均值作为最终结果.其中,根据第4.4 节实验,集成GBDT 的参数设置为:集成的GBDT 个数为15,采样率为0.9,每个GBDT 的迭代次数为100,学习步长为0.2,决策树最大深度为6.

分类结果用混淆矩阵表示,如图4 所示.分类效果如表7 所示.从表7 可以看出,单一GBDT 的分类F1-score 较其他3 种分类器高出10 %～ 14 %;进行集成后查全率和召回率比单一GBDT 提高了约1 %,效果最佳.

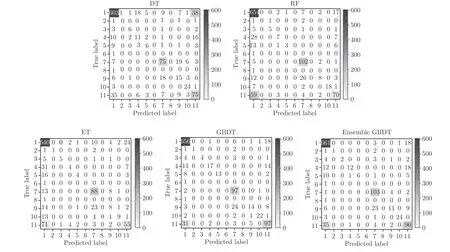
图4 混淆矩阵Fig.4 Confusion matrix

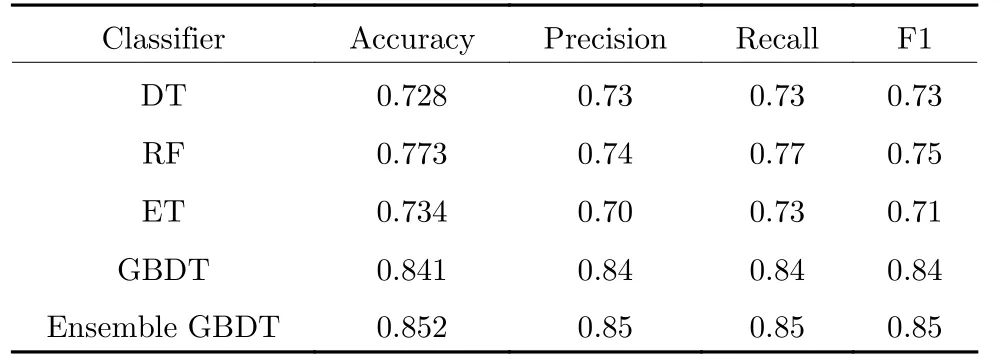
表7 各分类器性能对比Table 7 Performance comparison of classifiers

因集成GBDT 在每个GBDT 训练时随机选择训练样本,降低了样本类别失衡造成的影响,且将Bagging 与Boosting 结合的方式充分考虑了模型过拟合问题,提高了模型的泛化能力,从而提高了分类的准确率,故而效果最优.

4.6 特征选择实验结果及分析

本文根据特征重要度进行特征选择,将选择特征按重要度排名分组累加,代入模型重新训练,以进行事故致因分析.为验证特征选择的有效性及可靠性,在本节实验中进行了不同特征组合对事故类型预测结果的对比.将单一GBDT 训练中,特征重要性大于0.001 的特征筛选出来用于集成GBDT 模型训练,训练后的模型在测试集上分类准确率提高了1.6～1.8 个百分点,表明基于GBDT 的特征选择具有一定的可靠性.为进一步分析所选特征的正确性,将特征按重要度降序排列,以十个为一组依次累加代入集成GBDT 模型训练,结果如图5 所示.实验结果表明,随着特征数量的增多,分类准确率呈现上升趋势且逐步逼近于使用全部特征训练所得准确率,说明所选特征符合重要度排序.当特征数量大于30 时,分类准确率趋于平稳,表明之后增加的特征对预测结果几乎没有影响,进一步验证了特征符合重要度排序.

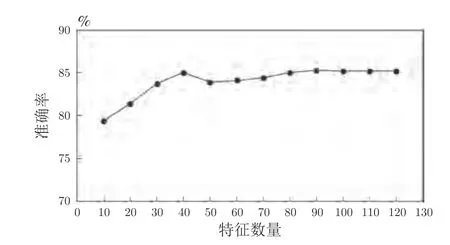
图5 不同特征数量下预测结果Fig.5 Prediction results of classifier with different features

为进行铁路事故成因分析,本文选择排名前15 的特征进行总结,如表8 所示.将这15 个特征按共性可划分为地理位置(Location)、速度(Speed)、里程(Mileage)、天气(Weather)、载货(Freight)、监管人员因素(Manager)六大类.以脱轨(Derailment)和碰撞(Collision)两类事故为例,综合进行事故成因分析,结果如图6 所示.由图6 可知,铁路事故发生与地理位置、列车行驶速度等有重要联系,温度和人员因素与事故发生也有一定联系.结果符合常规事故成因,具有可靠性.

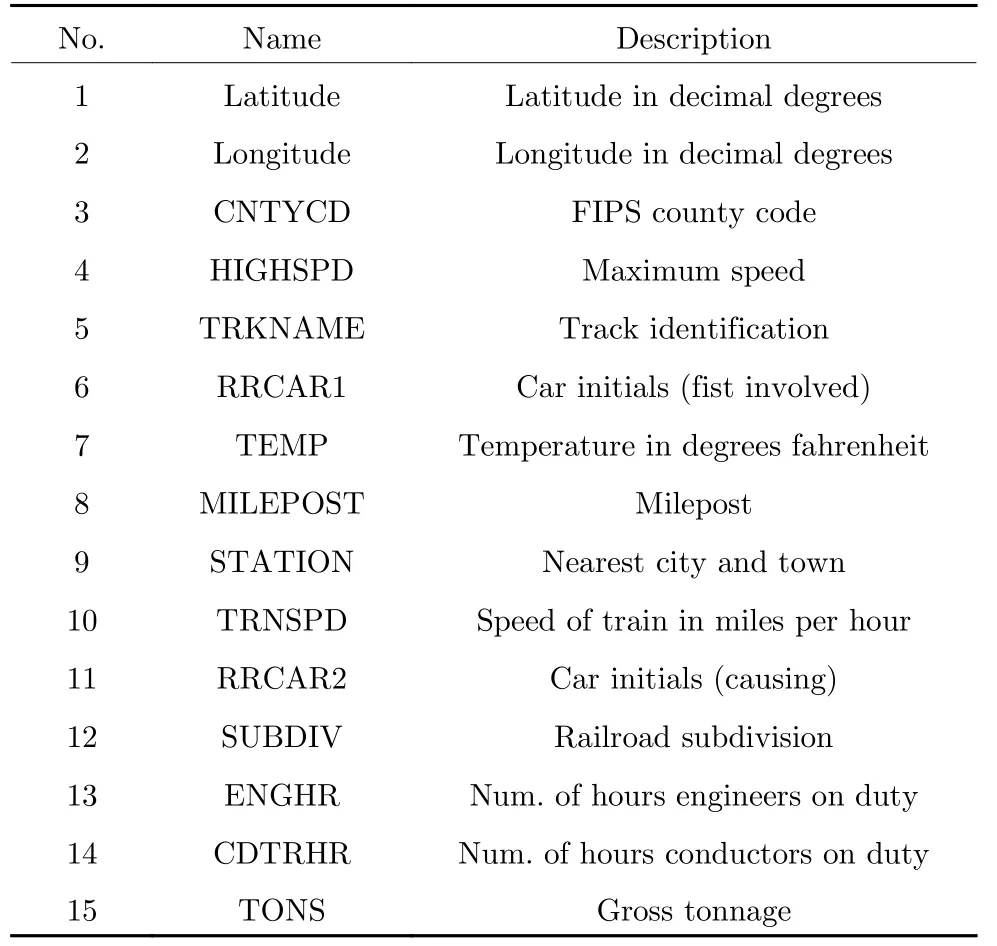
表8 重要度排名前15 的特征Table 8 Features of top 15 in importance

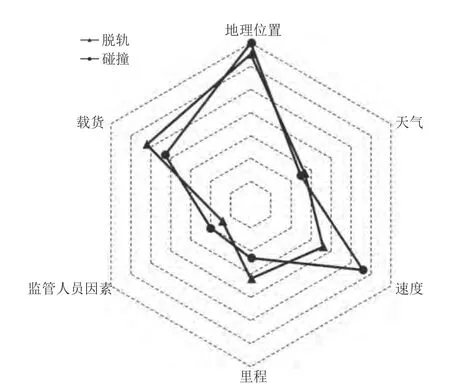
图6 两类事故致因中不同因素的比例Fig.6 Proportion of different factors in causes of two types of railroad accidents

5 结论

本文提出了一种基于GBDT 的铁路事故类型预测和成因分析模型.针对铁路事故记录数据缺失的问题,提出基于属性分布概率的补全算法,以保持原有数据结构,减少数据缺失对预测结果的影响.由于铁路事故数据存在类型失衡等问题,对预测结果也存在很大影响.为此,本文基于Bagging 对GBDT 进行集成,提高了单一GBDT 的预测精度.同时,结合统计分析的方法,根据特征重要度进行特征选择,进而对特征进行分析和总结,推测铁路事故成因,减少了人力的投入.实验证明,本文方法具有很好的可靠性和有效性.