基于KRR优化算法的油水系统中CO2溶解度模型

龙震宇, 王长权,2, 石立红,2, 叶万立, 刘 洋, 李一帆

1.长江大学石油工程学院，武汉 430100 2.油气钻采工程湖北省重点实验室(长江大学)，武汉 430100

0 引言

碳捕集、利用与封存(carbon capture, utilization and storage，CCUS)技术已经证实油藏是CO2地质埋存的最佳场所之一，油藏中CO2地质埋存不仅可以提高油气的采收率[1]，还可以有效缓解温室效应。CO2地质埋存形式分为4种：溶解封存、构造封存、游离封存以及矿物封存[2]。其中，溶解封存是指将CO2注入到地层中，与地层流体接触并溶解于油水系统中形成CO2-原油-地层水三相相平衡，将CO2埋存于地下；所以CO2在油水系统中的溶解度大小将直接影响CO2的封存潜力[3-4]。

调研发现，目前鲜有CO2在油水系统中溶解度模型方面的相关研究，而常采用基于CO2-原油[5-6]、CO2-地层水[7-12]两相相平衡的CO2溶解度模型直接计算后进行加权处理的方法，其计算结果与实际情况存在较大差异；因此开展CO2在油水系统中的溶解度模型研究具有实际意义。

本文利用高温高压PVT分析仪(高温高压流体物性全可视无汞分析仪)开展CO2在油水系统中的溶解度实验，基于实验结果，使用网格搜索法(GS)和贝叶斯优化算法(BOA)优化核岭回归算法中的正则化参数λ和核函数参数γ，将实验结果随机划分为训练集和测试集，并对模型进行训练、测试[13-16]，建立预测平均相对误差小且泛化能力较强的CO2在油水系统中的溶解度模型，再进一步利用该模型预测并形成不同温度、不同压力和不同油水体积比下的油水系统CO2溶解度图版，以期为CCUS技术的应用提供支持。

1 实验

1.1 实验样品及实验设备

实验用CO2纯度为99.99%；实验用油为吉林油田某井井口取得的地面油经实验室复配得到的地层原油，其组成见表1；实验用水是现场取得的地层水，其离子分析结果见表2。由表1、2可知：该地层原油C1摩尔分数为16.46%，C2—C6摩尔分数之和为15.50%，C7+摩尔分数为65.32%，属于普通黑油的流体组成；地层水水化学类型为CaCl2型，矿化度为4 128 mg/L，属于低矿化度地层水。

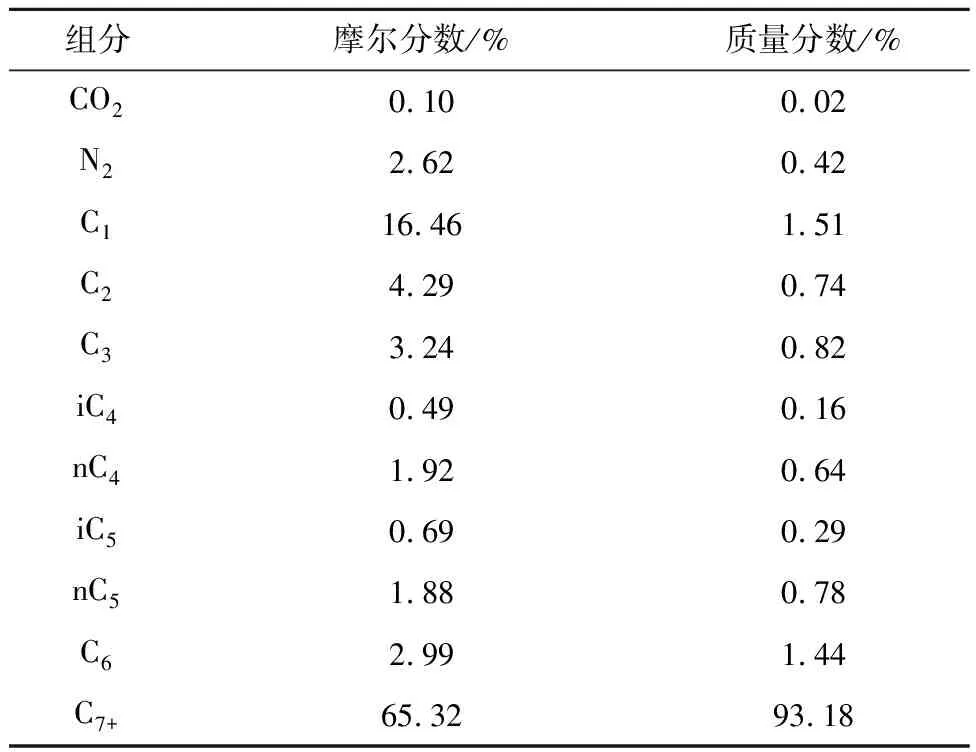
表1 地层原油组成

表2 地层水的离子分析结果

CO2-原油-地层水三相相平衡溶解度实验是利用高温高压PVT分析仪对不同油水饱和度条件下的CO2溶解度进行测试，主要的实验设备包括高温高压PVT分析仪、恒速恒压泵、气液分离器、气量计和电子天平等，各实验设备的精度足以满足实验测试的需要。实验流程见图1。

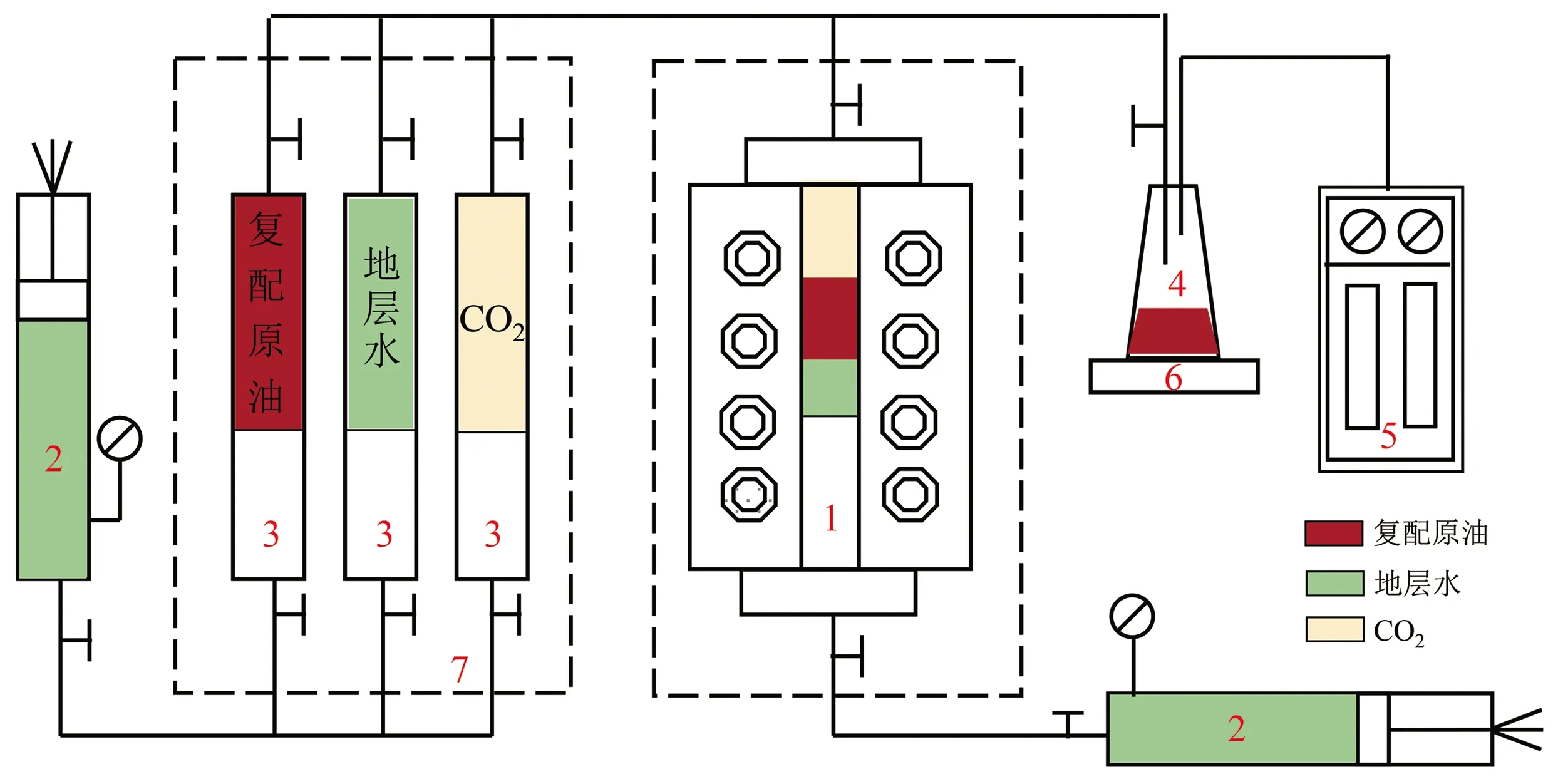
1.高温高压PVT分析仪；2.恒速恒压泵；3.中间容器；4.气液分离器；5.气量计；6.电子天平；7.恒温烘箱。

1.2 实验条件和步骤

利用高温高压PVT分析仪开展CO2在不同条件油水系统中的溶解度实验。实验过程中通过改变CO2注入量或油水体积比来明确不同因素对CO2在油水系统中的溶解度的影响。实验温度为94.7 ℃，CO2注入量7个级次分别为10%、20%、30%、40%、50%、60%、70%(按油相和CO2总的物质的量计数，下同)，油水体积比分别为7∶3、5∶5和3∶7，采用逐级注入方式注入CO2。其实验过程如下：

1)按油水体积比将一定量的原油和地层水分别输入到高温高压PVT仪中形成油水体系，搅拌至稳定后计量其总体积。

2)按CO2注入量设计级次将第1级的CO2注入到油水体系中，摇匀稳定后计量体积变化，并测定CO2注入后的饱和压力；再将第2级的CO2注入到混合体系中，再次测定其饱和压力；以此类推，直到设计的7个级次CO2全部注入结束后停止实验。绘制不同饱和压力下相应的CO2注气量关系曲线，即为CO2在油水系统中的溶解度曲线。

3)按设计的油水体积比，重复步骤1)—2)，确定不同油水体积比条件下的CO2在油水系统中的溶解度曲线。

1.3 实验结果及分析

通过开展CO2在油水系统中的溶解度实验，测定了在94.7 ℃、不同油水体积比下CO2在油水系统中三相相平衡溶解度数据，实验结果见图2。实验结果表明：随着CO2注入量的增加，系统饱和压力升高，CO2溶解度也随之增大；油水体积比同样影响着CO2在油水系统中的溶解度，油水体积比越高，CO2溶解度越大。

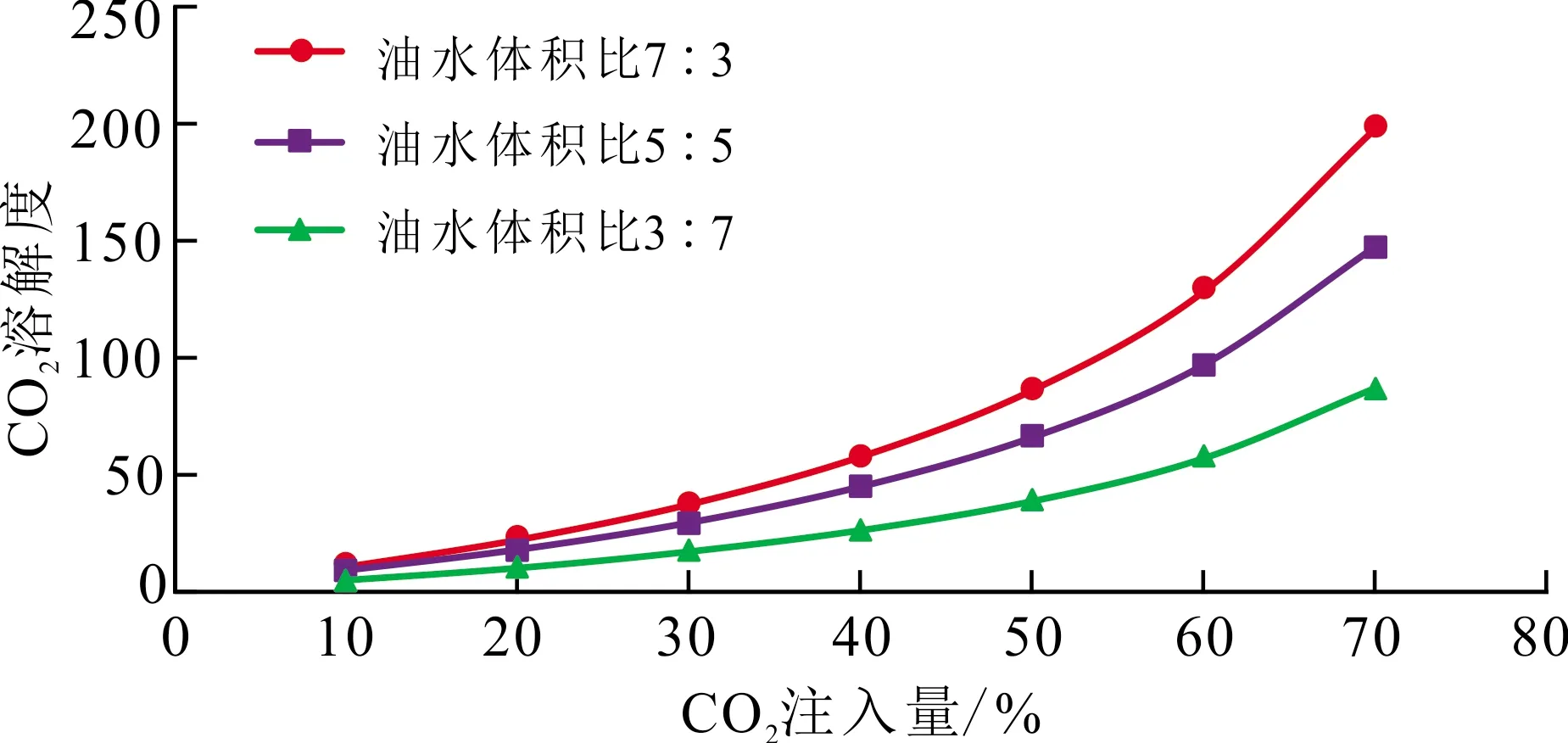
图2 CO2-原油-地层水三相相平衡下CO2溶解度原始数据

2 基于核岭回归预测

2.1 核岭回归原理

本研究采用的核岭回归算法(KRR)是由Cristianini等[17]在岭回归算法[18-20]上结合核函数提出的，其具有参数少、运行效率高等特点，对小样本问题有较好的拟合效果[21]。

核岭回归中将最小化均方差引入了正则化项来控制模型复杂度，目标函数见式(1)[22]：

(1)

式中：C为KRR算法的目标代价函数；i为样本数；yi为因变量；w为优化问题的参数矩阵；xi为自变量；λ为正则化参数。

核岭回归中引入了核方法，即从样本空间到特征空间的非线性变化，令xi转换为φ=φ(xi)，则优化问题的最优解表示为

(2)

式中：α为KRR算法的系数，根据选择的核方法确定；φ为所选用的核方法。

将式(2)代入式(1)中，用核函数K表示特征空间中的内积，整理矩阵形式可得到

(3)

将式(3)求导整理得到

α*=(K+λI)-1Y。

(4)

式中：α*为系数α的最优解；Y为l维的坐标向量，Y=(y1,y2,y3,…,yl)T，l为训练模型的数据样本数量；K为l行1列的核矩阵；I为单位矩阵。

则对于新样本x，可以得到估计值y：

y=α*·φ(x)。

(5)

2.2 模型评价

回归模型的评价通常选用均方根误差(ERMS)和平均相对误差(EMR)，计算方法如下：

(6)

(7)

式中：pi为预测值；oi为观测值。

2.3 KRR算法建模

以实验测定的油水体积比、CO2注入量、气油比、气水比、饱和压力作为输入量，以CO2溶解度实测值作为输出量，基于KRR算法建立初步CO2油水系统中的溶解度模型。

通过Python语言完成在原始数据中随机选出KRR建模所需的训练集和评估模型精度所需的测试数据。因为原数据集数据维度较大，为防止各样本点距离较大造成预测结果相近，将除了CO2溶解度外的特征值进行归一化处理，其计算方法见式(8)。

(8)

将Python语言处理后的数据传入默认的KRR模型进行建模，未优化的KRR模型主要参数有：核函数，类型为高斯核(rbf)函数;正则化参数(λ)，值为1;核函数参数(γ)，为1/n_features。划分的测试集及其预测结果的ERMS和EMR见表3。

表3 随机划分的测试集以及KRR模型的预测结果和评价

由表3可以看出，KRR预测CO2溶解度的值与实验值的平均相对误差高达45.393%，均方根误差达到了22.207，需要进一步对KRR的参数进行优化，得到精度更高的模型。

3 模型的参数优化

本文采用网格搜索法和贝叶斯优化算法对KRR模型的λ和γ进行优化：前者可以减少预测值的方差，λ越大表示正则化越强；后者定义了核函数对单个训练样本的影响程度，γ越大表示其他样本就越容易受到影响。网格搜索法操作简单，且对于小样本数据优化速度快，而贝叶斯优化算法在许多具有挑战性的问题上优于大多数的全局优化算法[23]。

3.1 网格搜索法优化KRR模型(GS-KRR)

网格搜索法的原理是指定多种参数的范围，利用该范围内的参数进行排列组合得到评价最好的模型。优化过程由Python的Sklearn模块实现，指定核函数为高斯核函数、λ和γ作为优化参数，λ和γ指定的范围均为[0.000 1,1]。建立模型和优化模型的流程见图3。网格搜索法将设定的参数按照一定间隔进行排列组合传入KRR模型中，将训练数据进行划分来验证当前参数组合的误差，通过对比不同参数组合的误差得到精度最好的参数组合并返回。

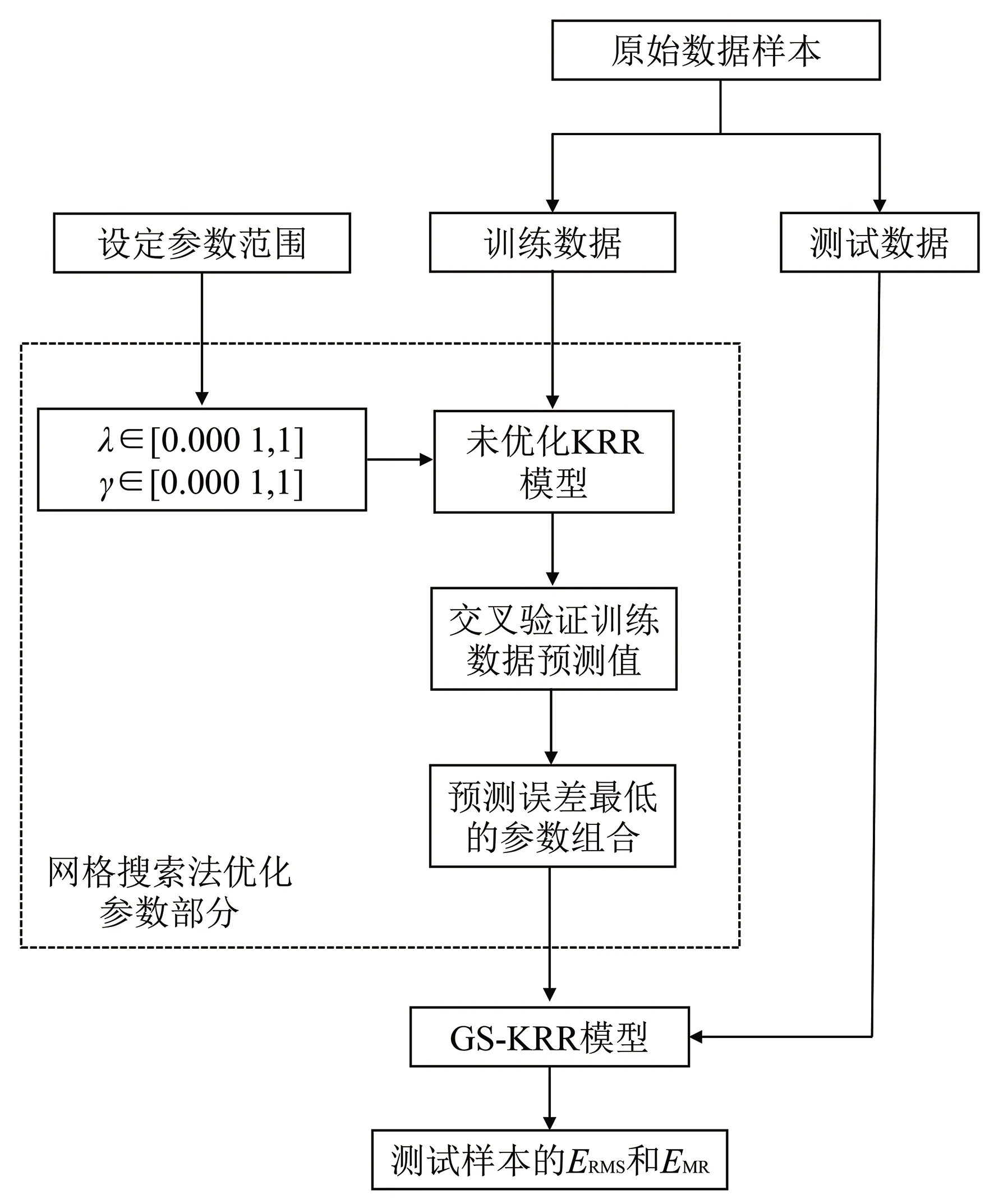
图3 GS-KRR建模过程

网格搜索法优化结果见表4，由表4可见，GS-KRR预测CO2溶解度的值与实际值的平均相对误差为6.758%，均方根误差为2.361，可见网格搜索法优化效果明显。

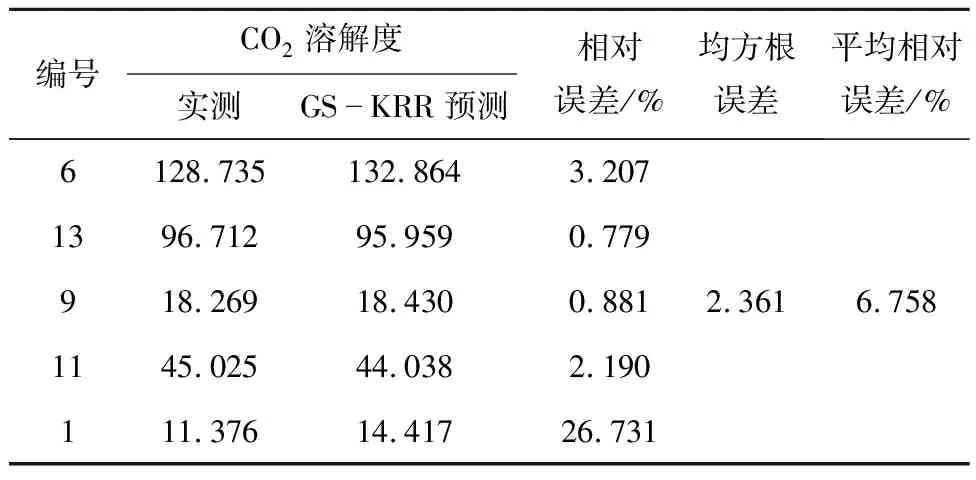
表4 网格搜索法优化结果以及评价

3.2 贝叶斯优化算法优化KRR模型(BOA-KRR)

贝叶斯优化算法充分利用被测试点忽略的前一个点的信息，根据先验分布假设采集函数,利用新采样点测试目标函数信息更新目标函数的先验分布，测试后验分布的全局最优值可能出现的位置点[24]。优化过程由Python的Bayes_opt模块完成，指定高斯核函数作为核函数、λ和γ作为优化参数，二者指定的范围均为[0.0001,1]。

贝叶斯优化算法的一般形式可以选取n个采样点作为先验，假设它们服从高斯分布，然后让i= 1,2,3,…,n执行如下循环：

1)根据最大化采集函数α选取下一个xi+1，xi+1=argxmaxα(x,Di)；

2)查询目标函数,获得yi+1；

3)整合数据集Di+1={Di,(xi+1,yi+1)}；

4)更新概率模型。

贝叶斯优化算法优化KRR参数的具体流程见图4。

图4 BOA-KRR建模过程

贝叶斯优化算法优化结果见表5。由表5可知，BOA-KRR预测CO2溶解度的值与实际值的平均相对误差为1.998%，均方根误差为1.635，对比未优化的KRR以及GS-KRR，可知BOA-KRR的效果最好。

表5 贝叶斯优化算法优化结果以及评价

4 模型推广——不同温度下三相相平衡CO2溶解度图版

由Python导入数据，分别建立在不同条件下三相相平衡CO2溶解度KRR模型、GS-KRR模型和BOA-KRR模型，通过模型评价对比，结果见表6。结果表明BOA-KRR模型的平均相对误差最低，最终确定使用BOA-KRR模型建立不同温度梯度、不同含水率下CO2-原油-地层水三相相平衡CO2溶解度图版。

利用训练好的BOA-KRR模型预测温度为35、45、55、65、75、85、95 ℃，油水体积比为7∶3、5∶5和3∶7，CO2注入量为10%～70%时CO2在油水系统中的溶解度，并将预测数据汇总形成不同温度梯度、不同油比体积比下的油水系统中CO2溶解度图版(图5)。参考图5，可以根据油水体积比、温度、CO2注入量得到对应三相相平衡下CO2溶解度。

表6 各模型对测试集的预测值相对误差

Table 6 Predicted relative errors of each model to the test set %

图5 不同温度、油水体积比下的CO2-原油-地层水三相相平衡CO2溶解度图版

5 结论

1)相同油水性质条件下，随CO2注入量的增加，油水系统饱和压力升高，CO2溶解度增大；油水体积比越高，CO2溶解度越大。

2)基于CO2在油水系统中的溶解实验数据建立并优化后的GS-KRR模型和BOA-KRR模型具有较高精度，其平均相对误差分别为6.758%和1.998%，与未优化的KRR模型(平均相对误差为45.393%)相比，优化算法后的模型具有较高的精度和更强的泛化性。

3)利用优化效果最好的BOA-KRR模型进行计算，形成了不同温度、不同油水体积比下CO2在油水系统中的溶解度图版，可为CO2碳捕集、利用与封存技术的应用提供支持。