基于鲁棒性原理的碎石桩置换率优化
2022-03-10李晴芳
李晴芳,汪 柱,于 洋
浙江大学海洋学院,浙江 舟山 316000
0 引言
软土广泛分布在我国东部沿海地区,具有压缩性高、渗透性低和承载力低的特点[1-3],是工程中常见的不良地基。如何提高软土地基承载力并减小其压缩变形,一直是岩土工程中关心的问题[4-5]。在众多工程措施中,碎石桩具有造价低廉和施工方便的特点,得到了较为广泛的应用[6-7]。碎石桩与软土构成了复合地基,其加固效果(如工后沉降量的幅度)与碎石桩置换率关系密切。置换率越高,地基处理的效果越好;置换率越低,地基处理的效果越差。同时,置换率的高低也决定了地基处理成本的高低。如何在兼顾碎石桩处理效果与经济成本的同时确定置换率一直是工程界关注的热点问题。
近年来,国内外学者就碎石桩复合地基优化设计开展了大量研究工作。如:董金玉等[8]基于极差分析法分析了桩径、桩长和桩间距对超静孔隙水压力和孔压比的影响规律,得到了夯扩挤密碎石桩的最优加固方案;杨明辉等[9]利用正交设计理论,探究了碎石桩桩长和置换率对复合地基加固效果的影响程度,进而对各参数进行了优化设计;韩永强等[10]以桩长、桩径和置换率作为复合地基的设计变量,采用遗传算法提出了最低造价条件下的水泥粉煤灰碎石桩复合地基优化设计计算方法;Black等[11]在物理模型实验中发现,从沉降控制的角度来看,碎石桩最优置换率取值应该在30%~40%范围内;Madun等[12]研究了桩径和桩长对承载能力和沉降的影响,并在此基础上利用响应面方法确定了碎石桩最优桩径和桩长;张晓君等[13]选用强夯置换碎石桩复合地基承载力的极限状态方程,对随机变量的概率模型进行了分析,提出了一种可靠度设计方法;洪昌华等[14]考虑模型不确定性的影响,计算了碎石桩复合地基承载力的可靠度指标,并讨论了建立在可靠度基础上的置换率设计问题;Deb等[15]提出了一种基于结合模拟优化的软土地基多目标优化设计方法,认为模量比和碎石桩的极限承载力是优化设计的重要参数;覃伟[16]研究了不确定性条件下的碎石桩沉降问题,探究了固结系数、桩径及土体变形能力对可靠度结果的影响。
由上述研究可见,碎石桩的优化设计从开始的基于岩土参数确定性的优化设计,逐步发展到了考虑岩土参数不确定性的可靠度优化设计,取得了极大进展。然而,这些方法并未对地基处理成本这一工程中重要的优化因素进行考虑。目前关于这方面的研究报道尚不多见,Juang等[17]在2013年提出的岩土工程鲁棒性设计方法为解决这一问题提供了可能的途径。其针对岩土参数的不确定性和岩土工程鲁棒性开展了岩土工程优化设计,该方法已应用于边坡工程[18-19]、隧道工程[20]、基坑工程[21]和地质灾害防治工程[22-24]中。
本文在前人研究的基础上,将碎石桩置换率作为需要优化的参数,兼顾岩土参数不确定性和地基处理成本,综合考虑鲁棒性、安全性和经济性进行碎石桩优化设计,总结优化结果的影响规律,以期为岩土工程和地质防灾工程提供相应参考。首先采用单向分层总和法计算复合地基工后沉降量,并将其作为确定性计算模型;然后,考虑碎石桩和桩间土体压缩模量的不确定性,基于Monte-Carlo模拟方法获得不同置换率条件下地基工后沉降量的平均值及标准差,并控制满足复合地基安全性的工后沉降量平均值;再利用工后沉降量的标准差衡量鲁棒性,进而通过置换率量化地基处理的成本,优化碎石桩置换率;最后讨论了沉降量限值、压缩模量变异系数和参数分布模式对优化结果的影响规律。
1 地基工后沉降量计算方法
在碎石桩复合地基中,置换率(m)为碎石桩的横截面积与其所对应的影响区域面积之比:
(1)
De=αCs。
(2)
式中:Ac为碎石桩的横截面积,m2;A为碎石桩影响区域面积,m2;Dc为碎石桩的直径,m;De为碎石桩影响区域等效直径,m;Cs为两根碎石桩的中心间距,m;α为几何相关系数,当碎石桩分别按照三角形、正方形和六边形排列分布时,其对应取值分别为1.05,1.13和1.29。
工后沉降量是碎石桩复合地基设计时需要考虑的重要因素,可采用单向分层总和法计算[25]。将复合地基分为加固区与下卧层两部分(图1)。将加固区的沉降量记为S1,下卧层的沉降量记为S2。在竖向均布荷载作用下,复合地基的工后总沉降量S可表示为加固区沉降量与下卧层沉降量之和:

图1 碎石桩复合地基示意图
S=S1+S2。
(3)
为计算S1,将加固区中桩体和土体两部分视为一种复合材料,采用复合压缩模量来量化加固区的压缩性。将加固区分成n层,每层复合压缩模量为Ecsi,利用复合模量法计算S1:
(4)
Ecsi=mEc+(1-m)Esi。
(5)
式中:Δpi为第i层土的竖向附加应力平均值,MPa;Hi为第i层土的厚度,m;Ec为碎石桩的压缩模量,MPa;Esi为第i层桩间土体的压缩模量,MPa。
由分层总和法可计算S2:
(6)
2 碎石桩置换率鲁棒性优化设计方法
在岩土工程鲁棒性设计中,输入参数分为两类:一类是通过设计人员指定且易于控制的参数,称为设计参数,如碎石桩置换率m;另一类是具有不确定性且难以通过人为措施完全消除这种不确定性的参数,称为噪声因素。如果设计所对应的系统响应对噪声因素的变化不敏感,则认为该设计是具有鲁棒性的[26-27]。由于无法完全消除噪声因素的变化,岩土工程鲁棒性设计的本质是通过调整设计参数来减小系统响应的变化[26]。在本文中,通过调整碎石桩置换率,使复合地基的工后总沉降量对碎石桩压缩模量(Ec)和土体压缩模量(Es)变化不敏感。
在岩土工程鲁棒性设计方法中,要同时满足鲁棒性、安全性和经济性要求。文中碎石桩优化设计的目标是要在满足安全性的前提下,找到一个置换率,使得该置换率所对应的鲁棒性最优和工程造价最小[28]。然而鲁棒性最优和工程造价最小往往是相互冲突的。因此,Deb等[29]借助遗传算法提出了帕累托前沿(Pareto front)的概念,其由造价相同的方案中鲁棒性最优的方案构成,用于多目标优化设计,可在鲁棒性和工程造价之间进行权衡。为得到唯一的优化设计方案,可采用Khoshnevisan等[27]提出的最小距离法找到位于帕累托前沿上的关节点(knee point)。对于相互冲突的目标,它可以产生最优的折衷方案,即选出最优设计方案。最小距离法如图2所示,先找到实际并不存在的乌托邦点(Utopia point),该点代表具有最低的工程造价和最优的鲁棒性指标的设计方案,通过计算欧拉距离,找到帕累托前沿上到乌托邦点距离最小的点,其对应的设计方案就是综合考虑了鲁棒性、安全性和经济性3个方面的唯一设计方案,即关节点。为实现鲁棒性设计,要建立计算鲁棒性、安全性和经济性的评价指标。
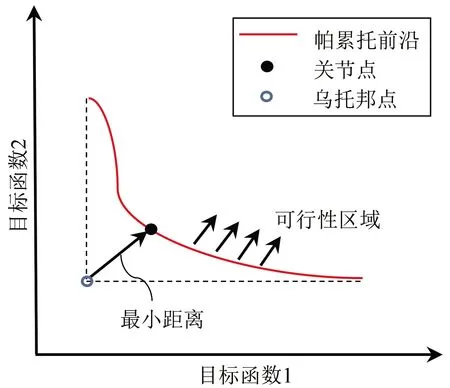
图2 最小距离法图示
2.1 鲁棒性指标计算方法
在鲁棒性设计方法中,通常采用信噪比、结构失效概率置信水平、系统响应梯度和系统响应变化等指标量化鲁棒性[27]。其中,系统响应变化可以直接反映出给定设计的系统性能对噪声因素的敏感程度,能够有效衡量其设计的鲁棒性。但考虑到工后沉降量是用来评价碎石桩复合地基施工稳定性的重要参数之一,本文以工后沉降量标准差作为鲁棒性评价指标,其数值越小,说明设计的鲁棒性效果越好。
文中,Ec和Es为噪声因素,根据其统计规律,利用Monte-Carlo模拟方法随机生成Ns组噪声参数,记为Xk(k= 1, 2, …,Ns)。对给定的置换率,每一组噪声参数所对应的沉降量可由式(3)—(6)计算得到,记为Sk(k= 1, 2, …,Ns)。基于可靠度理论[30-31],可求得Ns组工后沉降量的均值和标准差:
(7)
(8)
式中:Sμ为Ns组工后沉降量的均值;σs为Ns组工后沉降量的标准差。
一个置换率对应的工后沉降量的标准差越小,说明该置换率对碎石桩和土体的压缩模量的变化越不敏感,即鲁棒性越优。
2.2 安全性评价方法
通过工后沉降量的限值S0可评价设计的安全性。对于一个给定的置换率,如果其对应的工后沉降量的均值小于规定的工后沉降量的限值,则认为该置换率为一个可行的设计方案。针对所有碎石桩设计方案重复上述计算过程,便可从所有的备选置换率中得到可行设计方案。需要说明的是,安全性评价还可以根据需要考虑其他因素,比如碎石桩是否会在下卧层处发生刺入破坏等。工程实践和理论分析表明,碎石桩存在一临界桩长(约为碎石桩直径的4倍),当桩长大于临界桩长,碎石桩很少会发生刺入破坏[32]。出于说明的目的,本文假设所研究的碎石桩长大于临界桩长,因此不考虑刺入破坏。
2.3 工程造价计算方法
实际碎石桩复合地基的工程造价(C)主要包括施工组织、材料费用、设备租金和人工成本等。其准确计算方法具有地方特性。尽管没有统一的计算方法,但可以确定的是工程造价与置换率直接相关。因此,本文用置换率直接表示工程造价:
C=m。
(9)
3 置换率的优化设计流程
碎石桩置换率的优化设计流程分为5个步骤:
1)定义碎石桩复合地基设计问题,将优化设计所需的输入参数划分为设计参数和噪声因素。
2)确定备选的设计方案。根据设计参数(m)的典型取值范围、施工布置及类似工程经验,选择离散的设计参数,即备选的设计方案,方案的数目用M表示。
3)量化噪声因素的不确定性。基于碎石桩和岩土体参数力学特性的试验数据,结合文献及当地相似工程经验,评估Ec和Es的分布、均值与标准差。
4)计算工程造价和鲁棒性指标。对每一个设计方案,根据Monte-Carlo模拟方法随机生成Ns组噪声因素,利用式(3)—(6)计算得到Ns组工后沉降量,根据式(7)(8)计算这Ns组沉降量的平均值和标准差(鲁棒性指标)。如果沉降量的平均值小于沉降量限值,则该方案为可行的设计方案,进一步利用式(9)计算其工程造价。针对M组备选方案中的每一个设计方案,重复上述过程,得到所有可行设计方案。
5)依据帕累托前沿和关节点获得最优设计方案。根据4)计算的工程造价与鲁棒性指标,得到帕累托前沿,找到关节点,其所对应的设计方案就是最优设计方案。关于建立帕累托前沿和关节点的详细步骤可以参考文献[33]。
4 应用案例
采用昆明市某高速公路段第一合同段桩号K1+930断面[34]作为案例说明碎石桩置换率优化设计的方法与流程。该案例路基顶宽为25.0 m,路基两侧边坡比为1∶1.5,填土高度为5.0 m,路堤分布荷载为95 kPa。工程采用碎石桩处理软土地基,碎石桩呈正三角形分布,桩长(L)为15.0 m,桩径为1.0 m,桩间距为1.8 m。路基几何形状和下部土层分布如图3所示,相关参数如表1所示。出于说明性目的,将该工程工后沉降量的限值设置为75.0 cm,下一章将讨论该限值变化对优化结果的影响。
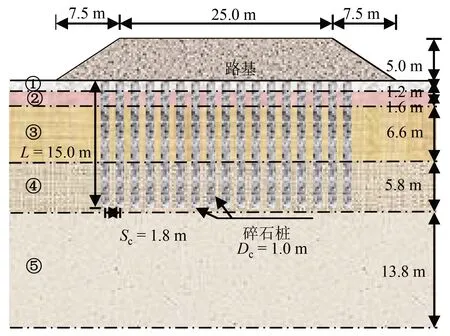
①填筑土;②淤泥质黏土夹亚黏土;③黏土及淤泥质黏土;④黏土;⑤黏土及淤泥质黏土。

表1 研究区碎石桩复合地基中的碎石桩和土体参数
假设Ec和Es均服从对数正态分布,Ec和Es的均值按表1取值。根据文献[35],碎石桩和桩间土体压缩模量的变异系数(f(Ec)和f(Es))分别取0.32和0.36。置换率的取值范围选为10%~50%,按1%的间隔取值,构成碎石桩置换率的41个备选设计方案。对每一个方案,利用Monto-Carlo模拟方法随机生成Ns组噪声因素数值。对每一组噪声因素,利用式(3)—(6)计算得到Ns组工后沉降量。Monto-Carlo模拟方法计算结果的精度随样本数量增加而提高,另外随计算精度提高,耗时也随之增加。为平衡计算精度和时间,计算了不同Ns值对应的工后沉降量平均值,如图4所示。由图4可见,当Ns值大于104.0时(图4虚线之后),工后沉降量的平均值基本趋于稳定。因此选择Ns= 104.0进行后续计算。

图4 随机样本数对碎石桩复合地基沉降量均值的影响
针对每个备选的置换率(共41个),根据式(7)计算出对应的工后沉降量平均值,若小于沉降量限值(75.0 cm),则认为该置换率为一个可行的设计方案,最终筛选出36组可行设计方案。对每个可行的设计方案,通过式(8)(9)计算工后沉降量的标准差(鲁棒性指标)和工程造价,得到图5所示的帕累托前沿。由图5可见:为提高设计的鲁棒性即减小工后沉降量标准差,需要更高的工程造价,因此需在经济成本和鲁棒性两者之间取得一个最优平衡。用前文提到的最小距离法确定最优设计方案,步骤如下。
1)对工程造价和鲁棒性指标(称为目标函数)进行归一化处理:
(10)
式中:Xj,max为第j个目标函数Xj的最大值;Xj,min为第j个目标函数Xj的最小值;XN为第j个目标函数Xj的归一化值。
归一化处理后,乌托邦点坐标为(0,0)(即工程造价最低,鲁棒性最优)。
2)根据最小距离法[25],计算帕累托前沿上每个可行设计方案对应点到乌托邦点的欧拉距离:
(11)

本文介绍的优化设计流程利用MATLAB程序语言实现,一般性能计算机均可完成。本例解算使用计算机配置为英特尔 Core i5-6200U@2.30 GHz 双核处理器、英特尔 HD Graphics 520主显卡、三星 LPDDR3 1867MHz 4GB×2内存,利用软件MATLAB R2017a,得出本案例最优置换率所用时长为14.75 s。
根据计算得到的欧拉距离,其最小值对应点即为关节点。图5中实心圆点为关节点,其对应的置换率为29%,为最优置换率。从设计与施工方便的角度考虑,可以根据工程造价在帕累托前沿上选取最优设计方案附近的置换率(如 30%)作为最终应用的置换率。

图5 双目标(鲁棒性和工程造价)优化条件下的帕累托前沿和关节点
5 讨论
5.1 沉降量限值对优化设计结果的影响
为明确沉降量限值S0对优化设计结果的影响,分别取沉降量限值为75、70和65 cm。图6展示了3种沉降量限值条件下的帕累托前沿和关节点,所对应的碎石桩置换率优化结果在表2中列出。
如图6所示,随着工后沉降量限值的减小,帕累托前沿上可行设计方案的数量减少;说明随着安全性要求的提高,由于置换率较低的碎石桩复合地基具有较大的沉降,不再满足安全要求。由表2可见,随着沉降量限值的减小即安全要求的提高,最优设计方案对应的工程造价升高;说明更严格的安全性要求需要投入更多的建造经济成本。

图6 3组不同沉降要求下的帕累托前沿和关节点

表2 3组不同沉降要求下的鲁棒性优化结果
5.2 压缩模量变异系数对优化设计结果的影响
岩土体参数往往存在极大不确定性,故实际工程中岩土体参数的变异系数往往难以确定,其取值也可能会对优化设计结果产生影响。首先,f(Es)数值取0.36并保持不变,改变f(Ec)数值为0.22、0.32和0.42,利用公式(10)进行归一化处理后得到帕累托前沿和关节点如图7a所示。同样,f(Ec)数值取0.32并保持不变,改变f(Es)数值为0.36、0.46和0.56,得到归一化处理后的帕累托前沿和关节点如图7b所示。
从图7可以看出,f(Ec)和f(Es)存在一个共同的变化趋势,即随着变异系数的增加,沉降量标准差增大,工程造价也增加;表明随着噪声因素的不确定性增加,鲁棒性变差,且工程造价增加。
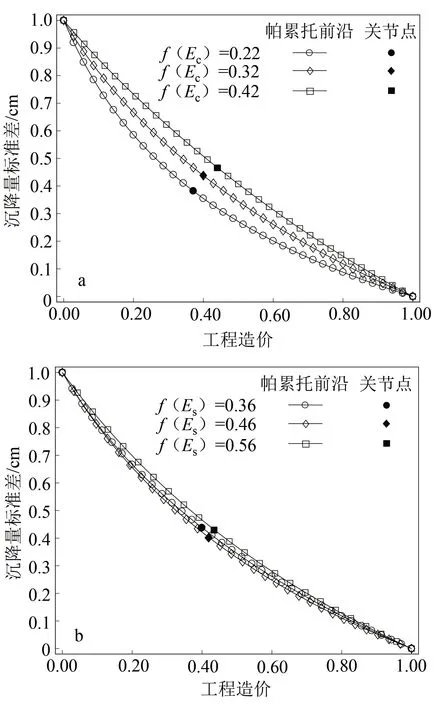
图7 不同桩体(a)和土体(b)压缩模量变异系数下的帕累托前沿和关节点
表3展示了f(Ec)和f(Es)都变化时对应的优化设计结果。由表3可见:与f(Ec)相比,f(Es)的变化对鲁棒性指标的影响程度更大,也就是说,工后沉降量对f(Es)的变化更加敏感;随着f(Es)的增加,可行设计方案数量减少幅度较大,说明随着f(Es)的增大,置换率较小的设计将不再满足安全要求。

表3 不同桩体和土体压缩模量变异系数下的优化结果
5.3 参数分布模式对优化设计结果的影响
岩土工程中常用的参数分布有正态分布和对数正态分布。前文假设噪声因素服从对数正态分布,此部分假设噪声因素服从正态分布,重复前文碎石桩综合优化设计流程解决本文工程实例置换率优化设计问题,优化结果如表4所示,可见最优置换率为32%。结合图5同时进行归一化处理后的优化设计结果如图8所示,总体上参数分布对优化结果的影响较小。相较于对数正态分布,利用正态分布处理时,沉降量标准差增加即鲁棒性变差,同时符合安全要求的可行性方案减少;这是由于正态分布模式下随机生成的噪声因素计算后对应的沉降标准差增加,置换率较小的方案计算得出的沉降量均值不再满足安全要求。从表4数据还可以看出:相较于对数正态分布模式,正态分布模式下最优设计方案对应的置换率和鲁棒性指标都明显增加。总结来说,正态分布处理后的噪声因素数值变化很大,由此计算得到的工后沉降量不确定性更高。

表4 两种不同参数分布模式下鲁棒性优化结果
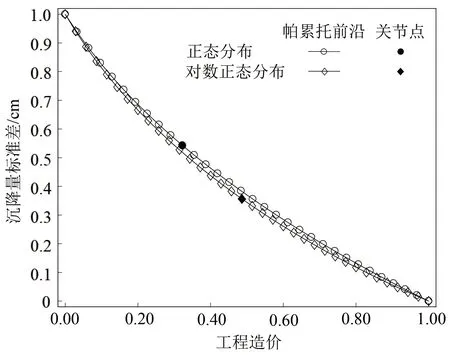
图8 归一化处理后不同参数分布模式下的帕累托前沿和关节点
6 结论
1)本文结合工程案例详细阐述了基于岩土工程鲁棒性的碎石桩复合地基置换率优化设计的方法和流程。经过上述优化设计流程得到最优置换率为29%,可实现鲁棒性和经济性的最优平衡。为施工方便,可在帕累托前沿上选取最优设计方案附近的置换率(如30%)作为最终工程应用值。
2)沉降量限值的变化会对最终优化设计方案产生影响,结果表明在实际工程中,需要投入更多的工程造价来满足更高的安全性要求。
3)碎石桩压缩模量和土体压缩模量对最终优化结果的影响为:二者的鲁棒性指标都会随变异系数的增加而增加,工程造价也随之提高;随碎石桩压缩模量变异系数的增大,可行方案数量无明显减少,鲁棒性指标增幅较小,而随土体压缩模量变异系数的增大,可行方案数量明显减少,并且鲁棒性指标增幅很大。
4)相较于对数正态分布,采用正态分布模拟噪声因素参数分布时,符合安全要求的可行性方案减少,最优设计方案对应的鲁棒性指标和工程造价均增大,其随机生成的噪声因素数值变化更大,由此计算的结果不确定性更高。
