Subterranean-SAE 算法的条件立方攻击*
2022-03-10陈思维张莎莎向泽军曾祥勇
刘 勇, 陈思维, 张莎莎, 向泽军, 曾祥勇
湖北大学 数学与统计学学院 应用数学湖北省重点实验室, 武汉 430062
1 引言
随着物联网应用等的大规模普及, 许多密码算法需要应用于低功耗、少存储的应用环境, 如射频识别卡标签(RFID tag)、传感器网络(sensor network) 和智能卡(smart cards) 等, 这催生了轻量级密码的研究与应用. 美国国家标准与技术研究院(NIST) 于2018 年开始征集轻量级密码算法加密标准, 该活动共接收到57 个算法. 截至2021 年3 月, 分别有56 和32 个算法成功进入第一轮和第二轮, 第三轮的10 个候选算法也已公布. Daemen、Massolino 和Rotella 设计的Subterranean 2.0 密码套件[1]是第二轮的32 个候选算法之一, 它包含哈希算法、认证加密算法和消息认证码等多种工作模式. 本文研究的Subterranean-SAE 是Subterranean 2.0 密码套件中的一种认证加密算法[1].
立方攻击(cube attack)[2]是Dinur 和Shamir 在2009 年EUROCRYPT 上首次提出的一种攻击方法, 它是高阶差分分析(higher-order differential cryptanalysis)[3]的一种变体, 被成功应用于分析各种对称密码[4–6]. 立方攻击主要分析输出比特在选定立方下的超级多项式(superpoly), 并从包含密钥信息的低次超级多项式中恢复密钥信息. 条件立方攻击(conditional cube attack)[7]是黄森洋等人在2017年EUROCRYPT 上提出的一种立方攻击变体, 该攻击的核心是寻找只有在所有条件等式成立时才为0的超级多项式. 无论是立方攻击还是条件立方攻击, 分析超级多项式是此类攻击的关键. 可分性(division property)[8]是目前恢复超级多项式的主要方法之一. Todo 于2015 年在EUROCRYPT 上首次提出基于字的可分性[8], 随后基于字的可分性被进一步精确为基于比特的可分性[9]. 紧接着, Todo 等人将比特可分性引入立方攻击[10], 与传统基于实验方法直接测试超级多项式不同, 可分性可以从理论上分析超级多项式的性质, 故基于可分性的立方攻击[10]不再受限于立方维数. 然而利用可分性进行密码分析需要刻画并搜索可分性传播, 向泽军等人在2016 年ASIACRYPT 上首次将混合整数线性规划(mixed integer linear programming, MILP) 引入可分性[11]. 该方法通过提出可分迹(division trail)[11]的概念解决了可分性传播的刻画,并将可分性的传播用一组线性不等式刻画,从而将可分性搜索转化成一个MILP 问题.相比于二子集可分性, 三子集可分性能更精确地描述可分性的传播. 王森鹏等人在2019 年ASIACRYPT上提出了三子集可分性的MILP 模型,并利用该模型进行了基于三子集可分性的立方攻击[12]. 随后,郝泳霖等人在2020 年EUROCRYPT 上研究了无未知子集的三子集可分性(three-subset division property without unknown subset), 提出了一种精确计算超级多项式的方法并成功应用于Trivium 等算法[13]. 胡凯等人在2020 年ASIACRYPT 上运用单项式迹(monomial trail) 的概念给出了三子集可分性的另一种刻画方法, 并成功恢复了842 轮Trivium 算法一个78 维立方的超级多项式[14].
目前, 已经存在许多针对Subterranean 2.0 密码套件安全性分析的公开文献. Subterranean 2.0 密码套件的设计文档对该算法的密码学性质进行了全面地评估, 包括差分分析(differential cryptanalysis)[15]、线性分析(linear cryptanalysis)[16]等. 2019 年, 刘富康等人分析了Subterranean-SAE 算法在三种攻击场景下的安全性[17]. 首先是在nonce 重用场景下的全状态恢复攻击, 其数据复杂度为213, 时间复杂度的上界为216; 其次是在nonce 不重用场景下4 轮空白轮的区分攻击, 该攻击的数据和时间复杂度分别为233和233; 最后是在nonce 不重用场景下4 轮空白轮的条件立方攻击, 其数据和时间复杂度分别为269.5和2122. 2020 年, 宋凌等人进一步研究了Subterranean-SAE 算法密钥流生成阶段的密钥流偏差、密钥吸收阶段的状态碰撞和nonce 重用场景下的密钥恢复攻击[18]. 本文在上述研究工作的基础上进一步研究Subterranean-SAE 算法抗条件立方攻击的安全性强度.
1.1 本文的贡献
刘富康等人的条件立方攻击首先构造了一个65 维的条件立方, 并且假设当条件变量满足条件时, 输出代数次数为64; 否则为65[17]. 但是代数次数在不同情形下能否达到64 或65 并没有被验证. 基于上述问题, 本文首先研究了Subterranean-SAE 算法代数次数的评估方法, 提出了在初始状态未知场景下评估输出代数次数的新技术. 利用该技术, 本文成功评估得到4 轮空白轮Subterranean-SAE 算法的输出代数次数上界为63, 因此刘富康等人构造的条件立方攻击输出立方和恒为0, 即基于条件立方的密钥恢复攻击实际为区分攻击.
为了进一步构造有效的条件立方攻击, 本文提出了降低立方维数、扩展立方变量选取范围的立方搜索策略, 利用该策略本文共搜索得到24 组33 维立方. 由于本文构造的条件立方攻击的维数在实际可行的计算范围内, 因此我们通过实验验证了所构造条件立方攻击的有效性. 通过猜测部分密钥并利用构造的条件立方, 我们能够成功恢复剩余密钥比特, 该攻击的数据和时间复杂度分别为241.8和2124.
表1 给出了本文攻击结果与已有结果的对比. 在nonce 不重用场景下, 文献[17] 和本文均为4 轮空白轮(总共8 轮) Subterranean-SAE 算法的条件立方攻击. 在nonce 不重用场景下, 这是首次实现4 轮缩减轮数Subterranean-SAE 算法的全密钥恢复攻击.
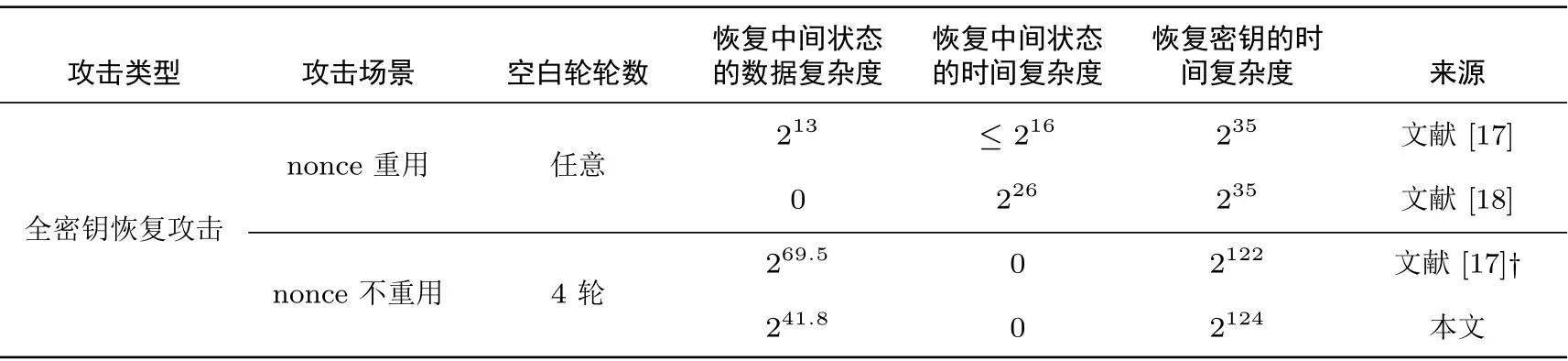
表1 本文结果与已有结果的对比Table 1 Comparison between proposed and known results
1.2 本文的结构
第2 节首先进行符号说明, 然后简单介绍Subterranean 2.0 密码套件的轮函数Subterranean-P 和Subterranean-SAE 认证加密算法, 最后介绍立方攻击、混合整数线性规划和基于可分性的立方攻击等相关知识; 第3 节主要介绍Subterranean-P 可分性传播的刻画和评估4 轮空白轮Subterranean-SAE 算法输出代数次数的方法; 第4 节提出Subterranean-SAE 算法改进的条件立方攻击并通过实验验证其有效性;第5 节对全文工作进行总结.
2 预备知识
2.1 符号说明


2.2 Subterranean-P
Subterranean 2.0 密码套件采用一个内部状态为257 比特的公开置换作为其轮函数, 本文记为Subterranean-P. Subterranean-P 总共包含四个操作, 其中χ操作为Subterranean-P 的非线性部件,ι、θ、π操作均为Subterranean-P 的线性部件, 记L=π◦θ◦ι◦χ, 则有如下表示:

其中, 当i=0 时,δ[i]=1; 否则δ[i]=0.
2.3 Subterranean-SAE 认证加密算法
首先介绍Subterranean-SAE 算法的两个核心函数.
吸收函数(duplex call, duplex(S,σ)): 首先对257 比特状态S执行一次Subterranean-P, 然后将不超过32 比特的信息流σ填充为33 比特(先填充1 个1, 再填充若干个0), 最后将σ[i] 异或到S[G[i]],其中G[i] 表示G的第i个元素, 如表2 所示.
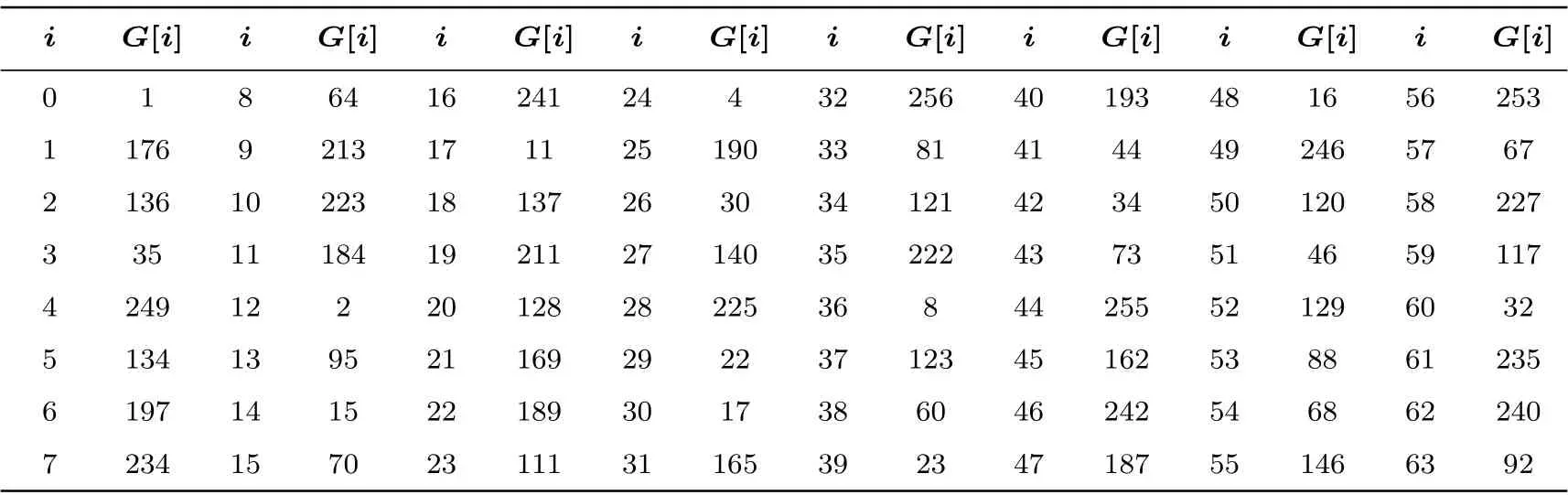
表2 G 表格的取值Table 2 Details of G
返回函数(extracted output, extract(S)): 返回32 比特数据S[G[i]]⊕S[G[i+32]](0≤i ≤31).
Subrranean-SAE 是Subrranean 2.0 密码套件中以Subrranean-P 为底层置换的一种认证加密算法,其密钥K、nonceN、认证标签(tag)T都为128 比特, 关联数据(associated date)A和明文P的长度不固定. 如图1 所示, 算法流程共包含如下7 个阶段, 算法详情见文献[1].
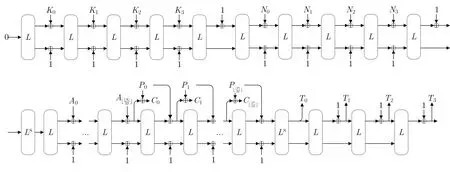
图1 Subterranean-SAE 的结构Figure 1 Structure of Subterranean-SAE
(1) 吸收密钥K阶段: 首先将128 比特的密钥K分成4 个32 比特密钥块K0,K1,K2,K3, 然后利用duplex(S,σ) 将这些密钥块吸收到状态中, 最后需要执行1 次duplex(S,NULL) 更新内部状态, 其中NULL 表示长度为0 的块;
(2) 吸收nonceN阶段: 首先将128 比特的nonceN分成4 个32 比特nonce 块N0,N1,N2,N3,然后利用duplex(S,σ) 将这些nonce 块吸收到状态中, 最后需要执行1 次duplex(S,NULL) 更新内部状态;
(3) 空白轮阶段: 执行8 次duplex(S,NULL) 更新内部状态;

(6) 空白轮阶段: 执行8 次duplex(S,NULL) 更新内部状态;
(7) 返回认证标签T阶段: 利用extract(S) 返回32 比特认证标签T0,T1,T2,T3, 在每次返回32 比特认证标签Ti(0≤i ≤3) 之间, 都需要执行1 次duplex(S,NULL) 更新内部状态.
2.4 立方攻击与混合整数线性规划

其中q(x,v) 的每一个单项式不含集合{vi0,vi1,··· ,vi|I|-1}中至少一个元素. 定义立方CI是遍历立方变量{vi0,vi1,··· ,vi|I|-1}的2|I|种取值的集合, 则f(x,v) 关于CI求和满足:
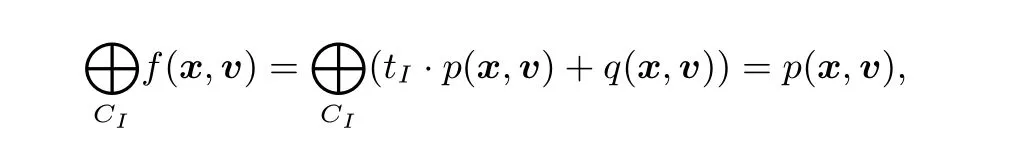
条件立方攻击是立方攻击的变体, 此攻击主要分为预处理阶段和在线阶段. 攻击者在预处理阶段通过选取合适的立方和条件变量构造有效的条件立方区分器, 使其满足当条件变量满足条件时立方和为0, 否则立方和不为0; 在攻击的在线阶段, 攻击者遍历预处理阶段选定立方变量的所有可能取值从而求得立方和, 并通过立方和是否为0 判断条件变量的取值. 若这些条件变量涉及秘密变量, 则可恢复部分秘密变量信息. 在实际进行立方攻击或条件立方攻击时, 分析超级多项式为核心步骤.
可分性是目前恢复超级多项式的有效方法之一. 基于字的可分性是Todo 在2015 年提出的一种一般化的积分性质[8], 可用于构造对称密码更长的积分区分器. 随后, Todo 等人在2016 年提出基于比特的可分性, 并且将比特可分性分为二子集可分性和三子集可分性[9].

MILP 是一类特殊的线性规划, 能用于高效搜索密码算法的相关密码学性质. Mouha 等人在2011 年将MILP 运用在搜索基于字的对称密码算法活跃S 盒的下界[19]. 随后, MILP 被应用于差分分析[20,21]、线性分析[21]、不可能差分分析[22,23]、零相关线性分析[22]和积分攻击[11,24]等. 利用MILP 搜索密码算法的相关密码学性质时首先需要将密码学性质的传播用一组线性不等式进行刻画; 然后通过选取合适的目标函数构造一个完整的MILP 模型; 最后借助公开的自动求解优化器Gurobi[25]搜索密码算法的相关密码学性质.
2.5 基于可分性的立方攻击
文献[10] 首次提出基于可分性的立方攻击, 建立了二子集可分性和立方攻击之间的联系. 由于三子集可分性描述可分性的传播更精确, 文献[12] 建立了三子集可分性和立方攻击之间的联系, 并提出了如下定理:


由推论1 可知, 可分性可用于精确恢复超级多项式的代数正规型(ANF), 进而推断出该超级多项式的代数次数. 在文献[13] 中, 作者提出了可分性关于复制、与和异或的可分性传播规则, 并用不等式组分别刻画了三个基本操作的MILP 模型. 此外, 文献[26] 研究了异或常数1 的可分性传播规则, 并用不等式组刻画了异或常数1 的MILP 模型. 在本文中:
不等式组COPY(b,a0,a1,··· ,am-1) 表示将变量b复制成m个变量a0,a1,··· ,am-1(即b=a0=a1=···=am-1) 的MILP 模型.
不等式组AND(a0,a1,··· ,am-1,b) 表示将m个变量a0,a1,··· ,am-1进行与操作得到变量b(即b=a0·a1·····am-1) 的MILP 模型.
不等式组XOR(a0,a1,··· ,am-1,b) 表示将m个变量a0,a1,··· ,am-1进行异或操作得到变量b(即b=a0⊕a1⊕···⊕am-1) 的MILP 模型.
行台,即行尚书台。霸府行台,是由控制朝政的强臣组建的行台。霸府行台实际上是不受皇权约束、驾凌于皇权之上的,是为强臣控制政权服务的。北魏霸府行台从孝庄帝建义元年(528年)尔朱荣担任北道大行台开始,先后经历了尔朱仲远、尔朱兆、尔朱天光等尔朱氏霸府行台,高欢霸府行台和宇文泰霸府行台。下面讨论一下这些论霸府行台首长的特征
不等式组XOR(a,1,b) 表示将变量a和常数1 进行异或操作得到变量b(即b=a ⊕1) 的MILP 模型.
3 评估4 轮空白轮Subterranean-SAE 算法输出的代数次数上界
由于文献[17] 的条件立方攻击假设当条件变量满足条件时, 输出代数次数为64; 否则为65. 为了验证该条件立方攻击的有效性, 本节研究4 轮空白轮Subterranean-SAE 算法的输出代数次数评估.
3.1 构建4 轮空白轮Subterranean-SAE 算法的MILP 模型
利用2.5 节给出的可分性传播规则, 可将刻画Subterranean-P 可分性传播的MILP 模型分为以下三个部分, 具体细节如图2 所示:

图2 Subterranean-P 和吸收nonce N 的MILP 模型Figure 2 MILP model for Subterranean-P and absorbing nonce N

由算法流程可知, 在进行4 轮空白轮之前, 内部状态需以异或的方式对nonce 信息(N0,N1,N2,N3)进行吸收. 由于本节是对4 轮空白轮输出比特关于nonce 变量(N1,N2,N3) 的代数次数进行评估(见图3), 因此需要考虑(N1,N2,N3) 的可分性对整体可分性传播的影响. 另外, 在吸收nonce 的同时, 状态的某个比特还需要与常数1 异或. 令向量nr= (n0r,n1r,··· ,n31r) 表示nonceNr+1的可分性, 其中0≤r ≤2, 则刻画吸收nonceNr+1可分性传播的MILP 模型为:
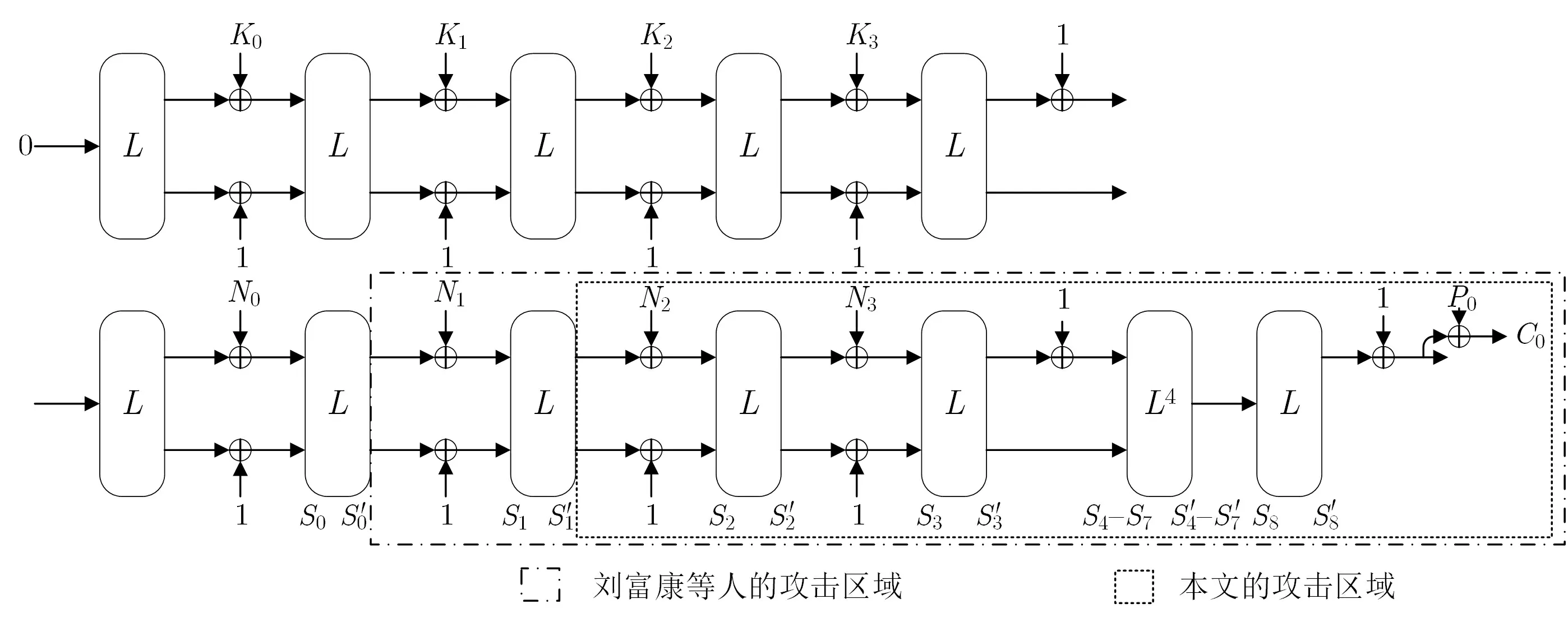
图3 Subterranean-SAE 算法条件立方攻击的攻击区域Figure 3 Attack areas of conditional cube attacks for Subterranean-SAE


3.2 评估4 轮空白轮Subterranean-SAE 算法输出的代数次数上界
由于刘富康等人攻击区域的初始状态S′0(如图3) 的257 比特均包含密钥信息(即未知), 且本文利用已有的技术无法在有限计算资源下评估出输出代数次数, 故本文提出定理2, 用于初始状态未知场景下的输出代数次数评估.

证明: 由于MILP 模型中刻画可分性u的约束条件的取值区间完全包含刻画可分性u′的约束条件的取值区间, 所以uf→1 的可分迹条数一定大于等于u′f→1 的可分迹条数. 故若无未知子集三子集可分性满足uf→1 的可分迹条数为0, 则满足u′f→1 的可分迹条数也一定为0.
假设固定立方变量不变, 对于MILP 模型中未知比特的可分性无任何约束条件时模型无解, 即可分性迹条数为0, 那么由定理2 可知, 无论初始状态未知比特的真实取值如何, 其对应输入可分性传播到特定输出可分性的可分迹条数也一定为0. 类似的, 在其他状态位不变的情况下, 假设MILP 模型中对于nonce的非立方变量可分性无任何约束得到模型无解, 那么无论nonce 中非立方变量真实取值如何, 其对应的可分迹条数也一定为0.
通过以上分析, 构建用于评估4 轮空白轮Subterranean-SAE 算法代数次数上界的MILP 模型具体流程如算法1 所示. 在算法1 中, 第1–11 行约束N1,N2和N3中立方变量的可分性为1, 非立方变量无任何约束条件; 第12–13 行约束输出可分性的汉明重量为1, 且输出可分性为1 的比特索引为op; 第15行表示利用3.1 节给出的MILP 模型对第i轮Subterranean-P 和吸收nonceN进行刻画; 第18 行表示模型的优化状态为Status. 若Status = 2, 表示模型有解; 若Status = 3, 表示模型无解; 若Status 为其他值, 表示模型报错. 在选定立方变量后, 若模型无解, 由定理2 可知输出比特SR[G[op]]⊕SR[G[op+32]]中对应的超级多项式为0, 进一步可推断输出比特SR[G[op]]⊕SR[G[op+32]] 的ANF 中不存在以立方变量乘积构成的单项式.

算法1 返回MILP 模型的优化状态Input: 轮数R, N1,N2 和N3 中立方变量索引集I0,I1 和I2, 输出比特索引op, 空MILP 模型M.Output: 模型的优化状态Status.1 for 0 ≤i ≤31 do 3 2 if G[i] ∈I0 then M.con ←ni0 = 1 4 end 5 if G[i] ∈I1 then M.con ←ni1 = 1 7 end 8 if G[i] ∈I2 then 6 M.con ←ni2 = 1 ▷约束N1,N2 和N3 中立方变量的可分性为1, 非立方变量无任何约束条件.10 end 11 end 12 M.con ←uG[op]9 R +uG[op+32]R = 1 13 M.con ←Σi∈{0,1,···,256}uiR = 1 14 for i = 0 to R-1 do 15 刻画第i 轮Subterranean-P 和异或nonce N 的可分性传播16 end 17 M.optimize()18 Status = M.Status()19 return Status ▷当Status = 2 时, 模型有解; 当Status = 3 时, 模型无解; 当Status 为其他值时, 模型报错.
为了评估输出代数次数上界, 需要多次调用算法1. 记N1,N2和N3中的立方索引集合分别为I0,I1和I2, 假设初始的立方变量数为n, 即|I0|+|I1|+|I2|=n, 若算法返回值为2, 停止调用算法1 且可推断代数次数上界为n; 若算法返回值为3, 则说明代数次数小于n, 此时需要从立方集合中移除1 个立方变量, 使得|I0|+|I1|+|I2|=n-1, 更新I0,I1和I2并继续运行算法1. 对于()种新立方集合, 如果至少存在1 种情况使得算法1 返回值为2, 停止调用算法1 且可推断代数次数上界为n-1, 否则代数次数小于n-1, 此时继续从立方集合中移除1 个立方变量, 重复以上步骤, 直到模型无解为止.
3.3 代数次数评估结果
记Ii0,Ii1和Ii2(0≤i ≤21) 分别表示文献[17] 的第i个立方中N1,N2和N3的立方变量索引集. 本文利用算法1 对4 轮空白轮Subterranean-SAE 算法输出代数次数的评估结果如表3 所示.
(1) 表3 中第2 行表示: 对于除第7 个之外的立方变量索引集, 32 个输出比特关于立方变量的代数次数上界为62;
(2) 表3 中第3 行表示: 对于第7 个立方变量索引集I70,I71,I72, 输出第0,2,3,4,6,7,9,11,13,16,17,18,19,20,21,22,23,24,25,26,29,31 比特关于立方变量的代数次数上界为62;
(3) 表3 中第4 行表示: 对于第7 个立方变量索引集I70,I71,I72, 输出第1,5,8,10,12,14,15,27,28,30比特关于立方变量的代数次数上界为63.

表3 算法1 的实验结果Table 3 Experimental results of Algorithm 1
从表3 中的实验结果可知, 任意选取文献[17] 中的立方变量集, 32 个输出比特关于立方变量的代数次数上界为63, 而文献[17] 中条件立方攻击的立方变量总数为65, 因此输出立方和恒为0. 此外, 文献[17]中第3 个立方索引集的I31包含{30,111,137,223},I32包含{2,4,11,15,17,22,30,35,64,70,95,111,128,134,137,140,165,169,176,184,190,197,211,213,223,225,234,241,249}, 与其区分攻击模型中的33 维立方区分器所选立方索引集完全一致, 而该区分攻击已通过实验验证其正确性. 所以文献[17] 中利用I30,I31,I32构造条件立方攻击时, 无论条件变量取值如何, 其输出立方和恒为0. 该结果从侧面印证了本文算法1 评估代数次数上界的正确性.
4 Subterranean-SAE 算法改进的条件立方攻击
由于文献[17] 的条件立方攻击被证实为区分攻击, 本节继续深入研究并提出4 轮空白轮Subterranean-SAE 算法可被实验证实有效的条件立方攻击.
本节采用降低立方维数、扩展立方变量选取范围的策略, 实现对4 轮空白轮Subterranean-SAE 算法条件立方攻击的改进. 本节通过在N2和N3中共挑选33 维立方构造4 轮空白轮Subterranean-SAE 算法条件立方攻击, 其中挑选的33 维立方要求当条件满足时, 立方和恒为0; 否则立方和取值不定. 通过分析Subterranean-P 不难发现, 经Subterranean-P 更新后状态的二次项由上一轮两个相邻状态相乘产生,所以为了降低输出关于立方变量的代数次数, 本节选择不相邻且在经过一轮状态更新后仍不相邻的状态比特作为立方变量, 而条件变量的选取则取决于立方变量. 如图3 所示, 搜寻立方变量及对应条件的具体步骤如下:
(1) 选择N2中的n2个比特N2[i0],N2[i1],··· ,N2[in2-1] 作为立方变量, 其他变量设为常数, 其中ij ∈{G[0],G[1],··· ,G[31]}(j ∈{0,1,··· ,n2-1}), 这些比特在S2互不相邻;
(2) 选择N3中的n3个比特N3[i0],N3[i1],··· ,N3[in3-1] 作为立方变量, 其他变量设为常数, 其中ij ∈{G[0],G[1],··· ,G[31]}(j ∈{0,1,··· ,n3-1}), 这些比特在S3互不相邻;
(3) 选择S2中的1 个变量S2[condition] 作为条件变量. 当条件变量S2[condition] 满足条件f(S2[condition]) = 0 (f(S2[condition]) =S2[condition] 或S2[condition]⊕1) 时,N2中的n2个立方变量经一轮传播后在S3互不相邻, 并且与N3中的n3个立方变量在S3不相邻; 当S2[condition] 不满足条件f(S2[condition])=0 时,S3一定存在相邻的立方变量.
通过重复以上步骤, 本文共搜索到24 组33 维立方, 如附录中表5 所示, 其中立方变量索引集I0和I1分别表示N2和N3的状态位. 需要注意的是, 本文的立方变量在N2和N3中选取, 文献[17] 的立方变量在N1,N2和N3中选取. 通过对比发现, 本文找到的24 组立方中有17 组立方的立方变量索引与文献[17] 中N1和N2的立方变量索引一致, 但挑选这些立方的nonce 块有区别. 此外, 本文在搜索立方的过程中增加了立方变量的选取范围, 即当条件满足时,N2和N3的立方变量在S2和S3都不相邻, 输出的代数次数最高为32; 但是当条件不满足时,N2的立方变量经1 轮传播后在S3相邻, 并与N3的立方变量在S3不相邻, 输出的代数次数最高为33.
由于本文挑选的立方维数均为33, 因此对于条件立方攻击的有效性, 可直接通过计算其在不同条件下输出的立方和进行验证. 对于附录中表5 的每个立方变量集合, 在无关联数据场景下(即关联数据的长度为0), 本文共选取22 组不同的密钥K0,K1,K2,K3进行立方求和实验. 对于每1 组密钥, 固定N3中非立方变量,N0,N1以及P0为常数0, 选取N2中非立方变量为任意常数, 对条件变量S2[condition] 满足和不满足条件分别进行64 次实验. 实验结果表明,在22×64=1408 次实验中,当条件变量S2[condition]满足条件时, 32 个输出比特立方和都恒为0; 当条件变量S2[condition] 不满足条件时, 32 个输出比特立方和存在不为0 的实验次数和概率如表4 所示. 该实验结果证实本文构造的条件立方攻击有效.

表4 条件立方攻击的实验结果Table 4 Experimental results of conditonal cube attacks
一旦构造有效的条件立方攻击后, 即可恢复条件变量(中间状态). 由表4 可知, 当条件不满足时, 立方和为1 依概率存在, 故需要进行多次立方求和实验来确定条件变量的真实值. 在恢复条件变量的过程中,N3中非立方变量以及N0,N1固定为常数0, 而N2中非立方变量选取不同的常数值. 条件变量(中间状态) 恢复后, 即可用以构造方程恢复密钥, 其具体步骤如下:

5 总结
在利用无未知子集三子集可分性评估输出代数次数时, 若攻击模型中初始状态的具体取值未知, 则构建MILP 模型时无法给出初始状态的约束条件. 本文首次提出一种在初始状态未知时利用MILP 模型评估输出代数次数的技术, 并证明了通过该技术构建的模型无解时, 无论初始状态的真实取值如何, 其对应的MILP 模型也一定无解, 即输出立方和为0, 由此可评估输出关于立方变量的代数次数上界. 在刘富康等人对4 轮空白轮Subterranean-SAE 算法进行的基于条件立方的密钥恢复攻击模型中, 初始状态均涉及未知的密钥信息. 我们成功将本文的代数次数评估技术运用于Subterranean-SAE 算法并证实刘富康等人的攻击实际为区分攻击. 进一步, 本文通过分析Subterranean-P, 提出了一种新的立方变量选取策略,并搜寻到了更多的条件立方. 利用这些条件立方, 可以对缩减至4 轮空白轮的Subterranean-SAE 算法进行全密钥恢复攻击, 并且本文通过实验验证了该攻击的有效性. 通过统计分析, 该攻击的正确率不低于99.83%. 在nonce 不重用场景下,这是首次实现4 轮缩减轮数Subterranean-SAE 算法的全密钥恢复攻击.
