汶川地震灾区小流域洪水模拟及不确定性分析

孙聿卿，郭晓军，陈兴长，张 菊

（1.西南科技大学环境与资源学院，四川绵阳 621000；2.中国科学院山地灾害与地表过程重点实验室/中国科学院水利部成都山地灾害与环境研究所，四川成都 610041；3.中国科学院青藏高原地球科学卓越创新中心，北京 100101）

引言

山洪不但直接威胁山区人民群众的生命财产安全，也是泥石流等山地灾害最直接的激发因素。“5·12”汶川地震后，山洪泥石流在震区小流域集中、大规模、频繁暴发，给人民生命财产造成巨大损失。如2010年“8.13”强降雨造成灾区各地暴发群发性山洪泥石流灾害，其中红椿沟泥石流冲出约7×105m3物质堵断岷江，文家沟冲出3×105m3物质淤埋清平乡场镇，均形成堰塞湖等链式灾害［1］；2013年“7·10”强降雨激发都汶公路沿线多个流域暴发泥石流，其中七盘沟冲出规模达7×105m［1］，洱沟冲出物质超过5×105m3［2］，造成岷江河道多处堵塞；2019年“8·20”强降雨再次导致该路段暴发泥石流，交通干线中断通行达2个月；2020年夏季的持续强暴雨再次造成大范围的山洪泥石流灾害。灾害预报是最直接有效的防灾减灾措施，具有重要的防减灾意义。而采用科学合理的方法进行洪水峰值流量计算，是山洪和泥石流预报的重要环节。

小流域的洪峰计算方面，目前有适宜于特定地区的经验公式、小流域计算公式和水文模型等方法。在汶川地震灾区，有学者通过设计不同频率的暴雨，利用水文模型对流域径流过程进行模拟［3］；通过水文观测和数值模拟，发现小流域径流峰值随降雨量的增加存在非线性激增现象［4］；基于流域清水流量，采用雨洪修正法计算不同雨型条件下的泥石流流量变化特征［5］。但上述研究都存在一个共性问题，即没有用实际监测资料进行充分验证，而模型验证是水文计算中极为重要的部分，是保障计算准确性和科学性的基础。

汶川地震灾区小流域坡高谷深、地形复杂，降雨的空间不均匀性极大；自然环境艰苦、灾害频发，实际水文数据监测和获取极为困难。降雨和径流时间监测数据的缺失造成无法评估各种计算方法的合理性和所选择参数的准确性，因此，模型的应用存在很大的不确定性，体现在模型结构、模型输入及模型参数等各个方面［6-8］等。针对这个现状，本文作者对灾区一个典型小流域（洱沟一支沟）开展了数年的降雨和径流监测，并以该流域为研究对象，基于水文计算方法模拟径流过程，利用实际降雨和洪水监测资料，验证模拟过程，在此基础上探讨划分子流域和不同时间步长对模拟结果的影响，寻求该地区小流域洪水的最佳模拟方案。

1 研究区概况

选取四川省汶川县洱沟下游右岸支沟-禾家沟为研究对象。该小流域流域面积约2.4 km2，主沟道长约2.6 km，流域最高海拔为3 100 m，最低海拔为1 200 m，平均坡度达43.4°，沟道平均纵比降为280‰，流域整体自西南向东北方向延展（图1）。坡面的松散物质主要由古元古代康定岩群的斜长角闪岩、混合片麻岩、变粒岩等变质岩组成。该小流域可进一步划分为3个部分，W-I为流域下游，面积约0.7 km2，沟道长约1.3 km，沟道平均纵比降约为260‰；W-Ⅱ和W-III分别为上游2个支沟，W-II流域面积约1.3 km2，沟道长约1.2 km，沟道平均纵比降约330‰；W-Ⅲ流域面积约0.4 km2，沟道长约0.7 km，平均纵比降约380‰。

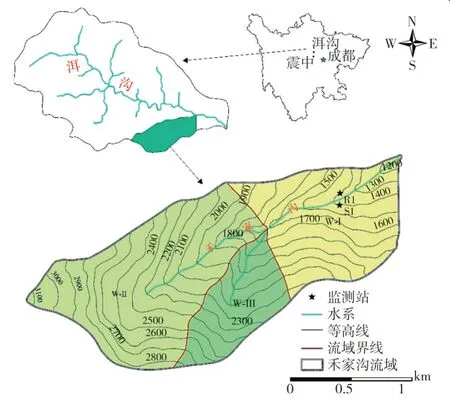
图1 研究区地形图Fig.1 Topographic map of the study area

流域沟口年平均降雨量约1 200 mm［2］。“5·12”地震对该流域造成严重的影响，大量的坡体垮塌物堆积于沟谷中，为山洪泥石流的暴发提供了丰富的松散物源。2013年7月10日和2019年8月20日，洱沟两次暴发大规模泥石流，冲出物质均超过5×105m3，掩埋沟口工厂等基础设施，且对岷江河道造成巨大影响；2014～2016年的实际监测表明，该流域多次暴发中小规模泥石流，且形成模式均以洪水径流冲刷沟床物质为主［2，9］，因而洪水流量的准确计算对于该流域及都汶地区类似流域的泥石流起动和流量估算都具有重要意义。

2 研究方法和数据来源

2.1 模拟方法

（1）模型构架

本文产流计算采用SCS曲线法，坡面汇流、河道汇流计算采用Kinematic wave（运动波）方程。SCS曲线是根据降雨累积量、土地利用现状、植被发育、土壤水分状况等因素发展而来的经验曲线［10］，其数学表达如下：

式中，Q为t时刻的产流量（mm），P为t时刻的累积降雨量（mm），Ia为初始损失量（mm），S为最大流域降雨最大潜在损失量（mm）。美国土壤保持局通过分析大量的降雨径流数据发现Ia与S的经验关系式为［10］：

而实际应用中将S定量表达为不同下垫面产流能力的综合指标-径流曲线数（CN）：

因此，用SCS曲线法分析产流过程的关键参数是CN值，即产流系数，与土壤类型、土地利用、土壤前期湿润程度等有关，通过C N值表可查算。一般地，产流系数越高，产流量越大［11，12］。

运动波方程原理是将流域概化为明渠，输入值为净雨量，基于此来计算明渠的非稳定水流方程，模拟其径流过程。表达式如下：

式中，h为水深（m），t为时间（s），q为单宽流量（m2/s），x为坡面某点距坡顶的水平距离（m）；ie（t）为t时刻坡面上距离坡顶x米处的单宽净雨量（mm），S0为坡面坡度，n为曼宁粗糙系数。

坡面汇流的主要参数为坡面长度、流域坡度、粗糙系数等，沟道汇流的主要参数为沟道长度、沟道坡度、沟道断面形状、曼宁系数等。基本的断面、尺寸信息通过影像或现场测量获得，曼宁系数可查表估算。

（2）流域模型和降雨输入

基于研究区5 m分辨率的地形数据，通过填洼、计算流向、汇流、生成河网、划分子流域、确定出水口等，提取河道长度、坡度、最长水流路径、流域坡度、流域面积、流域中心点位置等基本流域特征参数，最终获得流域地形模型。单次降雨模拟中，最重要的输入是场次降雨过程。根据流域内部实测监测资料，整理出需要的场次降雨过程，将实时降雨数据整理为5 min、10 min、30 min和60 min雨量序列作为模型的输入。

2.2 数据来源

研究所需数据来源于2014-2016年洱沟流域内部的降雨和径流监测数据。选择位于禾家沟流域内部的雨量站R1和位于禾家沟沟口的流量监测站S1（监测参数：流速和水位，见图1）。其中降雨监测利用0.5 mm的翻斗雨量计实时记录降雨过程，流体表面流速和水深分别采用雷达测速仪和超声波水位计监测，流量计算采用公式Q=a·V·A，其中a取0.6［13］，V表示流速，A表示沟道过水断面面积。

3 模型的总体计算效果

本文选取2014-2016年间的6场典型降雨数据进行模拟和验证试验，各次降雨的基本情况如表1所示。

表1 2014－2016年间各场次降雨情况Table 1 Rainfall in each session from 2014 to 2016

根据各场次降雨的雨型和总雨量，选取2015.8.16、2015.9.9、2015.6.7三场降雨作为模拟对象，用以大概确定模型参数范围，三场降雨的历时分别为6、13、14h，峰值雨强分别为37、22、23.5 mm/h，总雨量在91～99 mm之间。同时针对性选择2016.6.6、2015.6.22和2014.8.21三场降雨验证计算结果，各场次降雨历时分别为8、13、30 h，可代表短历时和长历时降雨，峰值雨强分别为89、21、17 mm/h，总雨量在92～197 mm之间。

模型需要的流域特征参数如坡面长度、坡度、河床宽度、河床长度等可通过实地考察和地形分析得到，计算过程参数如C N、坡面粗糙系数n1、沟道曼宁系数n2等可根据流域实际情况通过查表获得初始值作为参考，进而进行人工调整，以达到模拟效果的最优化。研究区地表土壤类型以砂黏土、砂土为主，上游植被覆盖主要是林地，中下游受到地震的影响，裸露滑坡体较多，部分滑坡体上逐渐有矮草和灌木丛恢复。参考美国水土保持局手册［10］以及目前国内外SCS模型应用的研究成果［14-17］，确定C N的初始输入值为70。根据研究区地表状态查表（USACE，1998）［10］选择粗糙系数0.3，曼宁系数0.08［9］作为初始值。退水过程的主要参数流量衰减系数初始值取0.9。划分子流域时，各子流域的初始基流量按流域面积大小分配。

首先将小流域视为一个整体进行集总式模拟计算，模拟时间尺度为5 min，径流过程见图2至图4（模拟过程线1），计算结果见表2。

图2 2015.8.16场次模拟过程Fig.2 The rainfall⁃runoff process simulation on Aug.16，2015

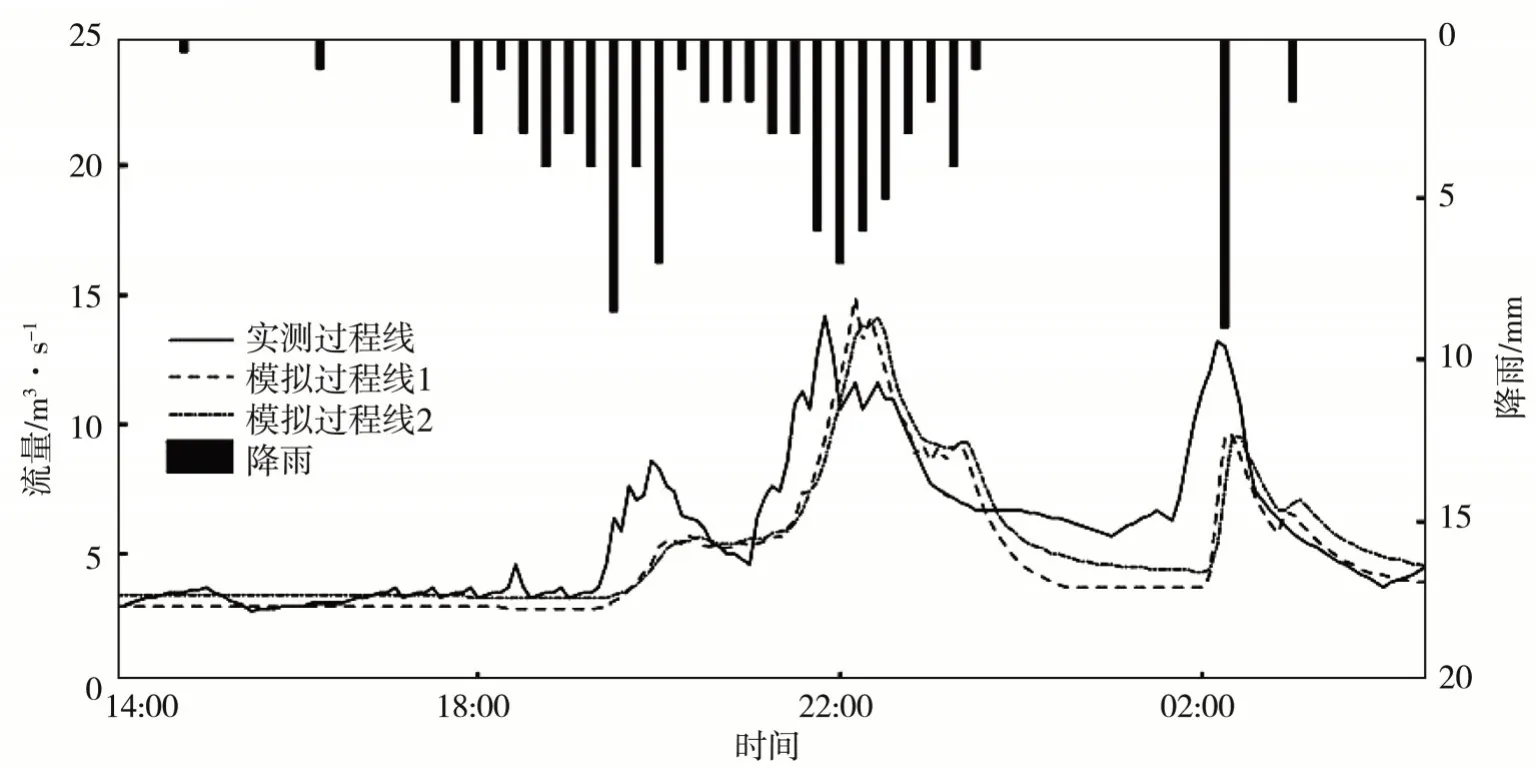
图4 2015.6.7场次模拟过程Fig.4 The rainfall⁃runoff process simulation on Jun.7，2015

本文针对的对象为降雨-洪水，在模拟效果的评价中，不以传统的Nash⁃Sutcliffe系数和相关系数R2等作为指标，而以洪水致灾最关心的3个要素：峰现时间、洪峰流量和洪水总量作为评价指标，三场降雨的模拟结果为：

（1）2015.8.16场次（图2）：模拟的径流过程线与实测的径流过程线基本一致；模拟的峰现时间比实测滞后5 min，洪峰流量14.8 m3/s，误差为4.23%，洪水总量20.8×104m3，误差为-4.09%。

（2）2015.9.9场次（图3）：该次洪水有两个峰值，模拟的径流过程线与实测的径流过程线基本一致，可模拟出两个峰值；第一次模拟的峰现时间比实测滞后5 min，洪峰流量14.6 m3/s，误差为1.39%，洪水总量30.0×104m3，误差为14.27%；第二次模拟的峰现时间与实测一致，洪峰流量11.2 m3/s，误差为1.82%。

图3 2015.9.9场次模拟过程Fig.3 The rainfall⁃runoff process simulation on Sep.9，2015

（3）2015.6.7场次（图4）：该次洪水有多个峰值，模拟的径流过程线与实测的径流过程线基本一致；第一次模拟的峰现时间比实测滞后20 min，洪峰流量14.9 m3/s，误差为4.93%，洪水总量25.3×104m3，误差为-15.88%；第二次模拟的峰现时间比实测滞后5 min，洪峰流量误差为-27.27%，洪峰值偏小。

由模拟效果可见，考虑到山区洪水数据获取和模拟的困难程度，3个关键指标的误差均在误差允许范围内。另外，本文在模型中选择的关键参数时，n1、n2基本保持一致，均为0.3、0.08，CN值在69～72之间，相对比较确定。因而，在验证阶段的3场降雨中，以CN=70，n1=0.3，n2=0.08作为初始参数，峰值流量误差均在3%以内，结果见图5至图7，证明了模型参数选择的合理性。若优化CN至最佳模拟效果，其取值也在69～72之间。

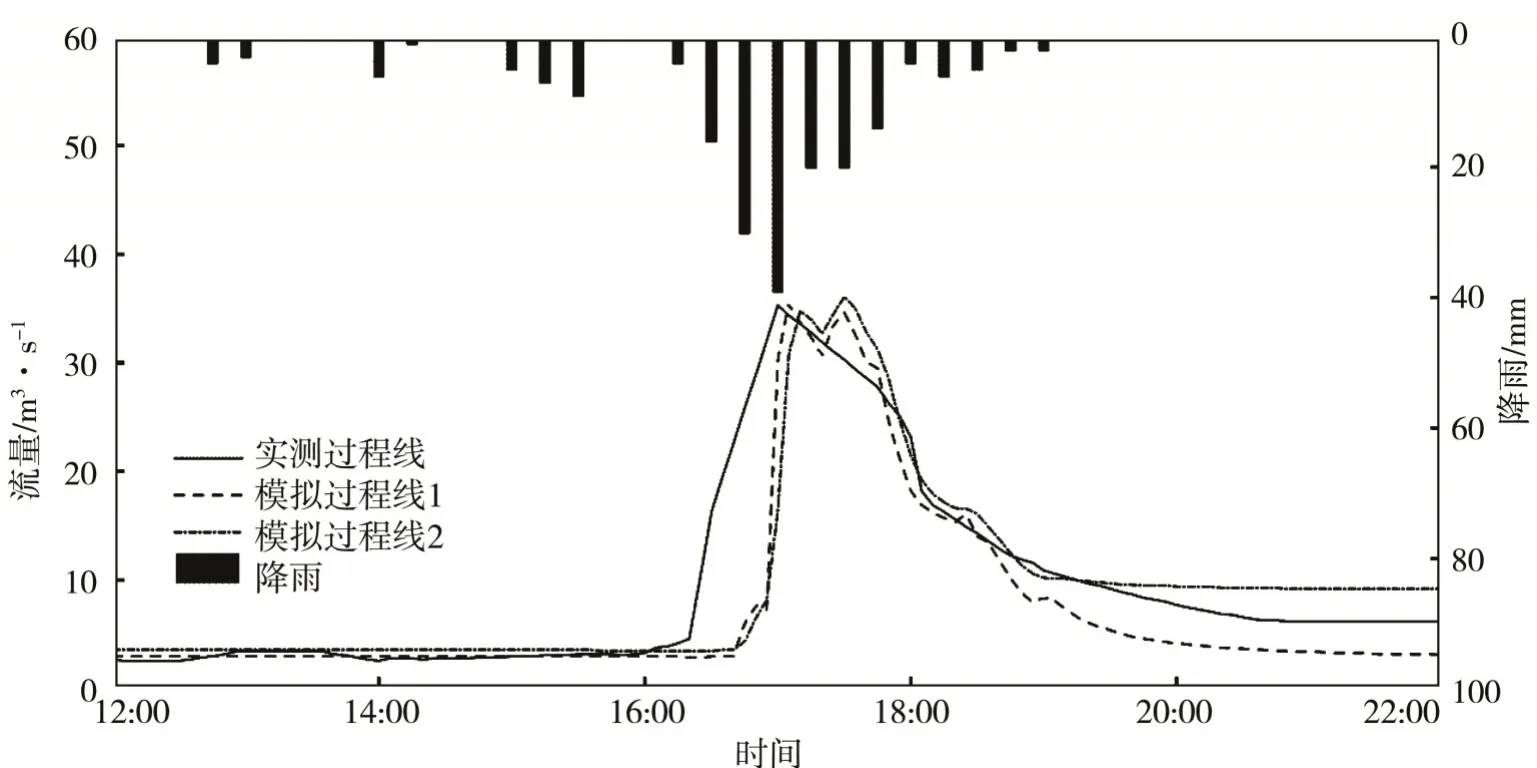
图5 2016.6.6场次模拟过程Fig.5 The rainfall⁃runoff process simulation on Jun.6，2016

图7 2014.8.21场次模拟过程Fig.7 The rainfall⁃runoff process simulation on Aug.21，2014

（1）2016.6.6场次（图5）：模拟过程线与实测过程线基本一致；模拟峰现时间比实测滞后5 min，洪峰流量35.5 m3/s，误差为0.57%，洪水总量25.9×104m3，误差为-22.79%；

（2）2015.6.22场次（图6）：模拟的径流过程线形态上虽与实测有一定差异，但模拟结果基本能反映峰现时间与峰值流量。峰现时间比实测滞后5 min，洪峰流量仅相差0.1 m3/s，洪水总量相比较偏小，误差为-14.31%；

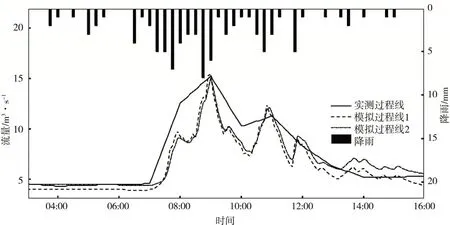
图6 2015.6.22场次模拟过程Fig.6 The rainfall⁃runoff process simulation on Jun.22，2015

（3）2014.8.21场次（图7）：模拟的径流过程线与实测的径流过程线基本一致，模拟结果能呈现多个洪峰，由于该场次历时较长，降雨过程复杂，模拟的后期洪峰流量与实测值仍存在一定偏差，洪峰值偏大；模拟的峰现时间比实测提前20 min，洪峰流量17.0 m3/s，误差为-2.86%，洪水总量77.2×104m3，误差为-0.9%。

综上，率定期和验证期的6个场次模拟结果显示，峰现时差范围为-20～20 min（峰现时间为正表示峰现时间滞后，为负表示峰现时间提前），洪峰流量误差范围为-2.86～4.93%，洪水总量误差范围为-22.79～-10.52%。考虑到山区洪水数据获取和模拟的困难程度，此3个关键指标的误差均在可接受范围内。同时，模型关键参数n1、n2基本一致，均为0.3、0.08，C N值在69～72之间，相对比较确定。由此可见，本文所选参数有效，模型可推广用于类似无资料地区的洪水估算。

4 子流域划分和时间步长对模拟结果的影响

4.1 划分子流域对计算结果的影响

为进一步探寻模型在小流域洪水模拟中的使用方案，将禾家沟流域划分为3个子单元进行分布式模拟，并与上述集总式模拟的结果相对比，以分析划分子流域与否对模拟结果的影响。三个子流域的CN值根据面积权重分配作为初始输入值：

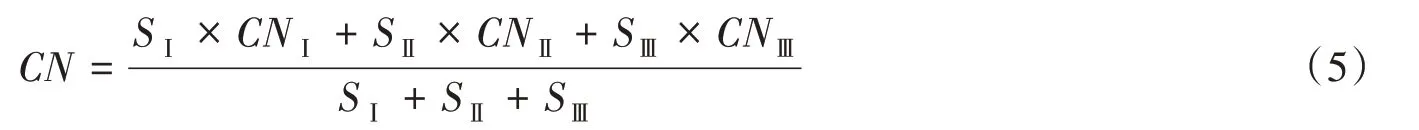
各场次模拟过程对比见图2至图7（模拟过程线2），模拟结果对比见表2。

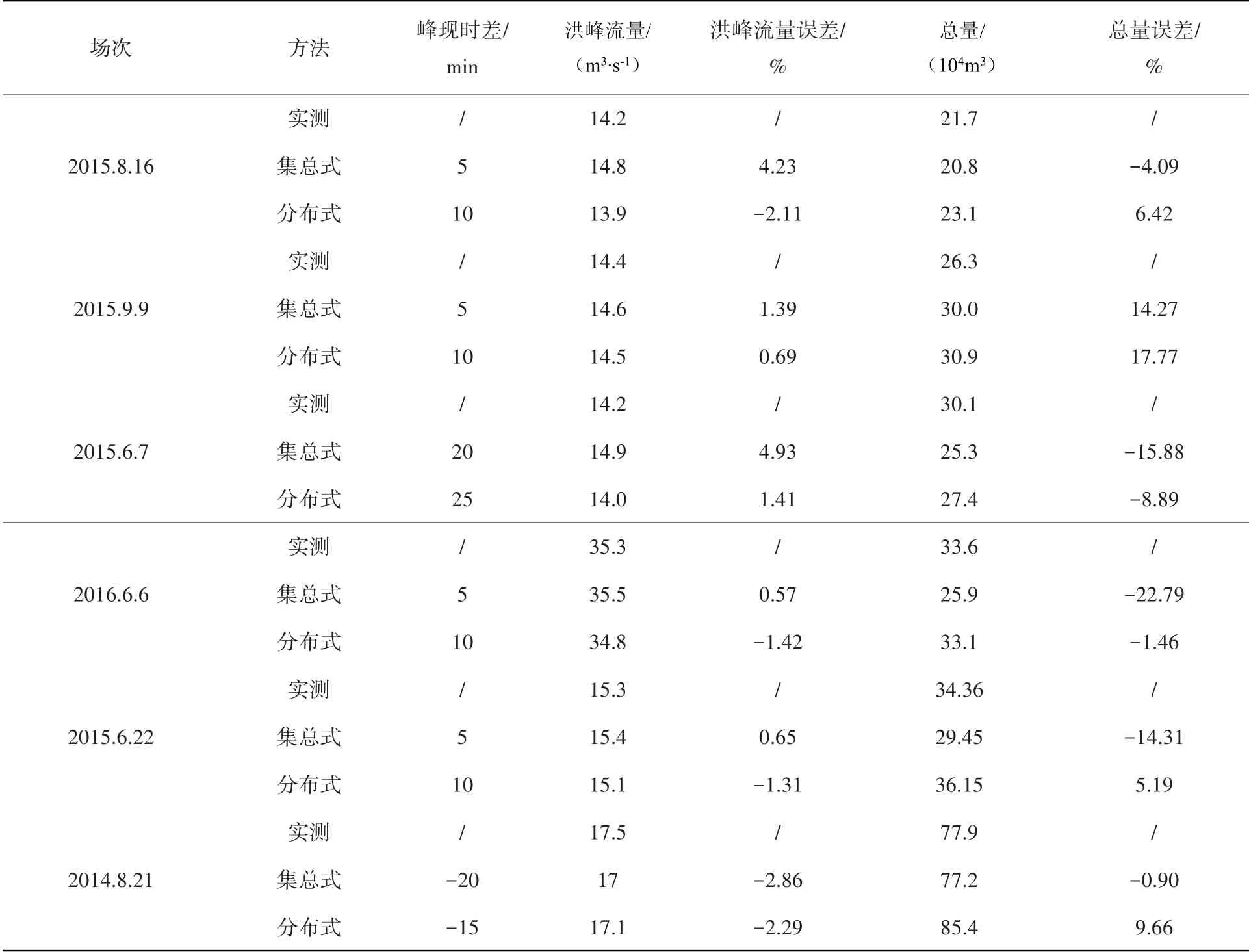
表2 各场次模拟结果汇总Table 2 Summary of simulation results of each rainfall event

结果显示，2种模拟方式的过程线基本一致；分布式模拟中洪峰流量误差范围为-2.29～1.41%，平均值为-0.83%，总量误差范围为-8.89～17.77%，平均值为4.78%。在峰值流量与洪水总量的模拟上比集总式模拟的精度有小幅度提升；峰现时差范围为-15～25 min，比集总式模拟往往有5 min左右的延迟，这是由于集总式模拟忽略了子流域内部汇流过程，而流域单元的细化考虑了子流域内部沟道的汇流过程，延长了河道汇演时间，导致峰现时间滞后。

考虑到分布式模拟在一定程度上增加了参数设置的工作量，在实际应用时往往造成参数难以确定，可能出现异参同效的现象，且对模拟结果的提升有限，在针对类似地形高差大、坡陡且参数难以获取的极小流域水文计算时，集总式模拟是简单易行的方案。

4.2 不同降雨时间步长对计算结果的影响

为探讨降雨输入的时间步长对模拟结果的影响，在参数不变的情况下，输入时间步长分别设置为5 min、15 min、30 min、60 min，分析6场降雨的洪水模拟过程，结果见图8～图13所示，各场次结果见表3。

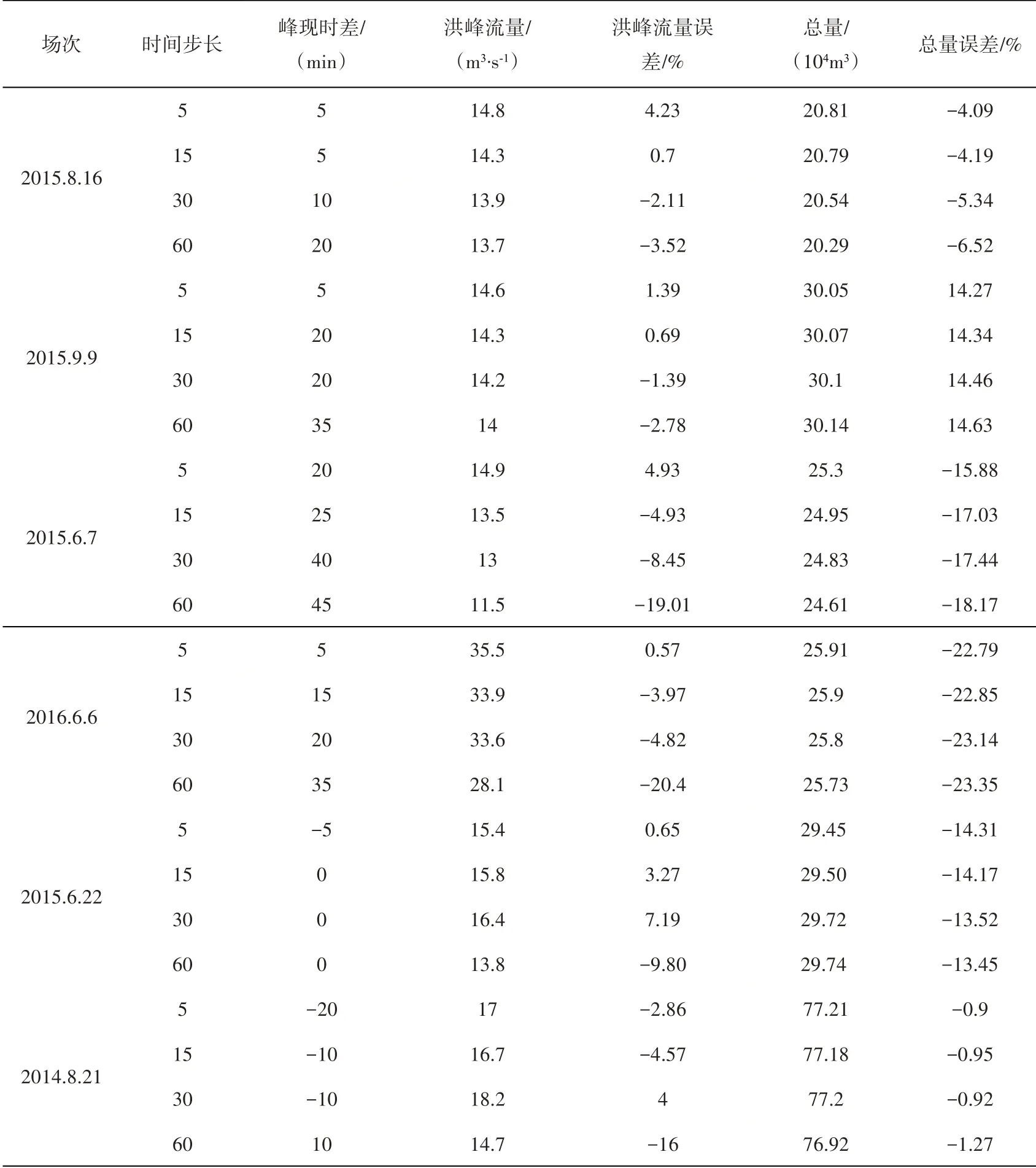
表3 不同时间步长下各场次的模拟结果汇总Table 3 Summary of simulation results of each rainfall event under different time steps

图8 不同时间步长下2015.8.16场次的径流过程对比Fig.8 Comparison of rainfall-runoff processes under different time steps on Aug.16，2015

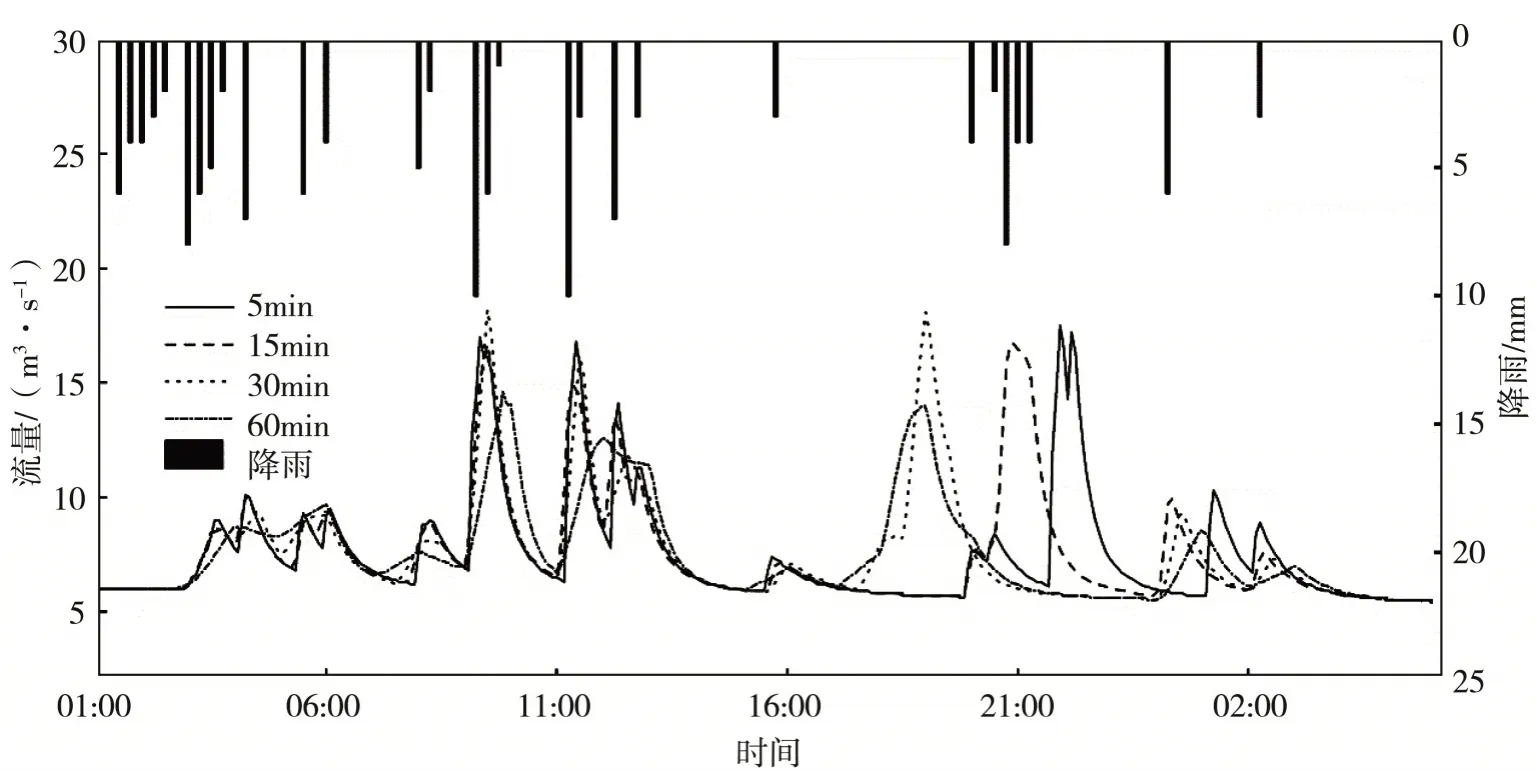
图13 不同时间步长下2014.8.21场次的径流过程对比Fig.13 Comparison of rainfall⁃runoff process of different time steps on Aug.21，2014

（1）2015.8.16场次（图8）：该场次不同时间步长的径流过程线基本一致；峰现时差范围在5～20 min之间，其中步长5 min和15 min的峰现时间一致，均滞后5 min，洪峰流量和洪水总量差距不大，总体逐步减小。

（2）2015.9.9场次（图9）：该场次不同时间步长的径流过程线在前期基本一致，第二次峰值差异较大，步长增加，洪峰值降低，过程线逐渐坦化；步长为5 min时洪峰现时滞后5 min，步长为15 min和30 min时洪峰现时均滞后20 min，60 min时滞后35 min，洪峰流量和洪水总量差异不大，总体趋势减小。

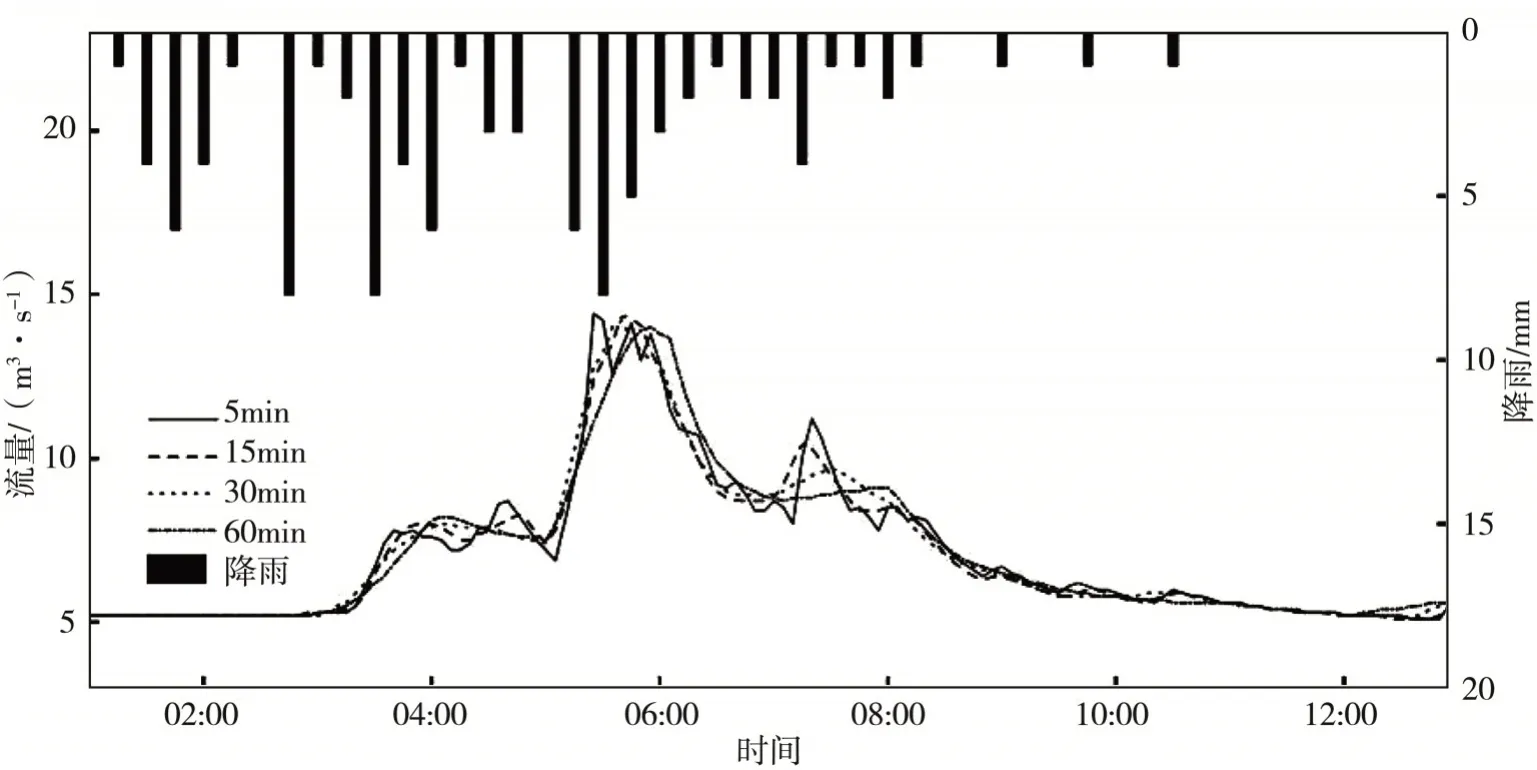
图9 不同时间步长下2015.9.9场次的径流过程对比Fig.9 Comparison of rainfall-runoff processes under different time steps on Sep.9，2015

（3）2015.6.7场次（图10）：该场次不同时间步长的径流过程线差异明显，步长为60 min的径流过程线更加坦化，峰值流量明显降低；步长越大，时差越大，滞后时间从20 min递增至45 min，洪峰流量和洪水总量逐渐减小。

图10 不同时间步长下2015.6.7场次的径流过程对比Fig.10 Comparison of rainfall-runoff process of different time steps on Jun.7，2015

（4）2016.6.6场次（图11）：该场次不同时间步长的径流过程线基本一致，相较步长为60 min的径流过程线更加坦化，趋于平缓；峰现时差从5 min递增至35 min，洪峰流量从35.5 m3/s递减至28.1 m3/s，误差从0.57%逐步变为-20.40%；洪水总量误差均保持在20%左右。

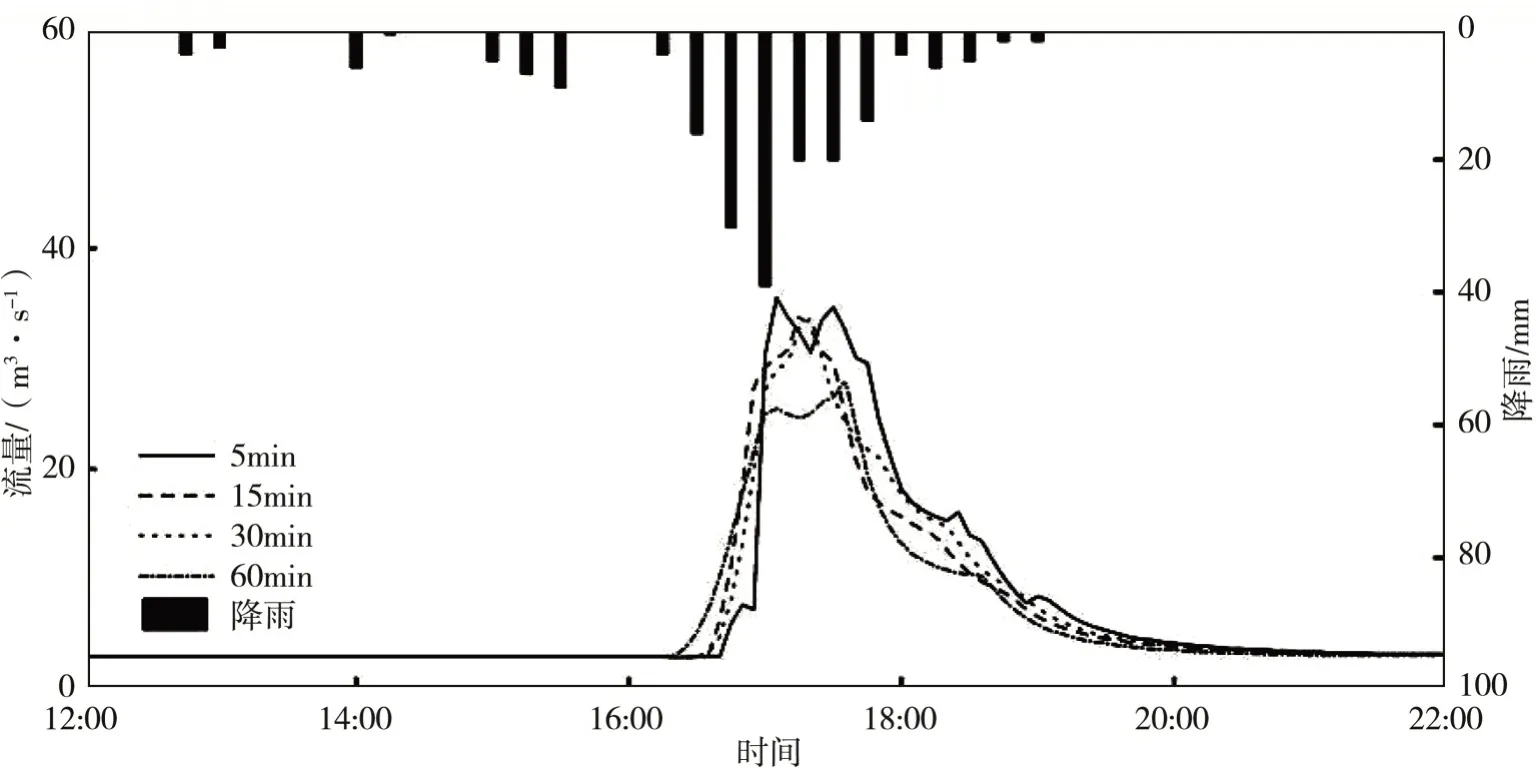
图11 不同时间步长下2016.6.6场次的径流过程对比Fig.11 Comparison of rainfall-runoff processes under different time steps on Jun.6，2016

（5）2015.6.22场次（图12）：该场次不同时间步长径流过程线的形态基本一致，步长为60 min的径流过程线有一定坦化；步长为15、30、60min的峰现时间一致，但相比5 min是滞后的，洪峰流量以及洪水总量，前3个步长差异不明显，但当步长增加到60 min时，峰值明显降低。

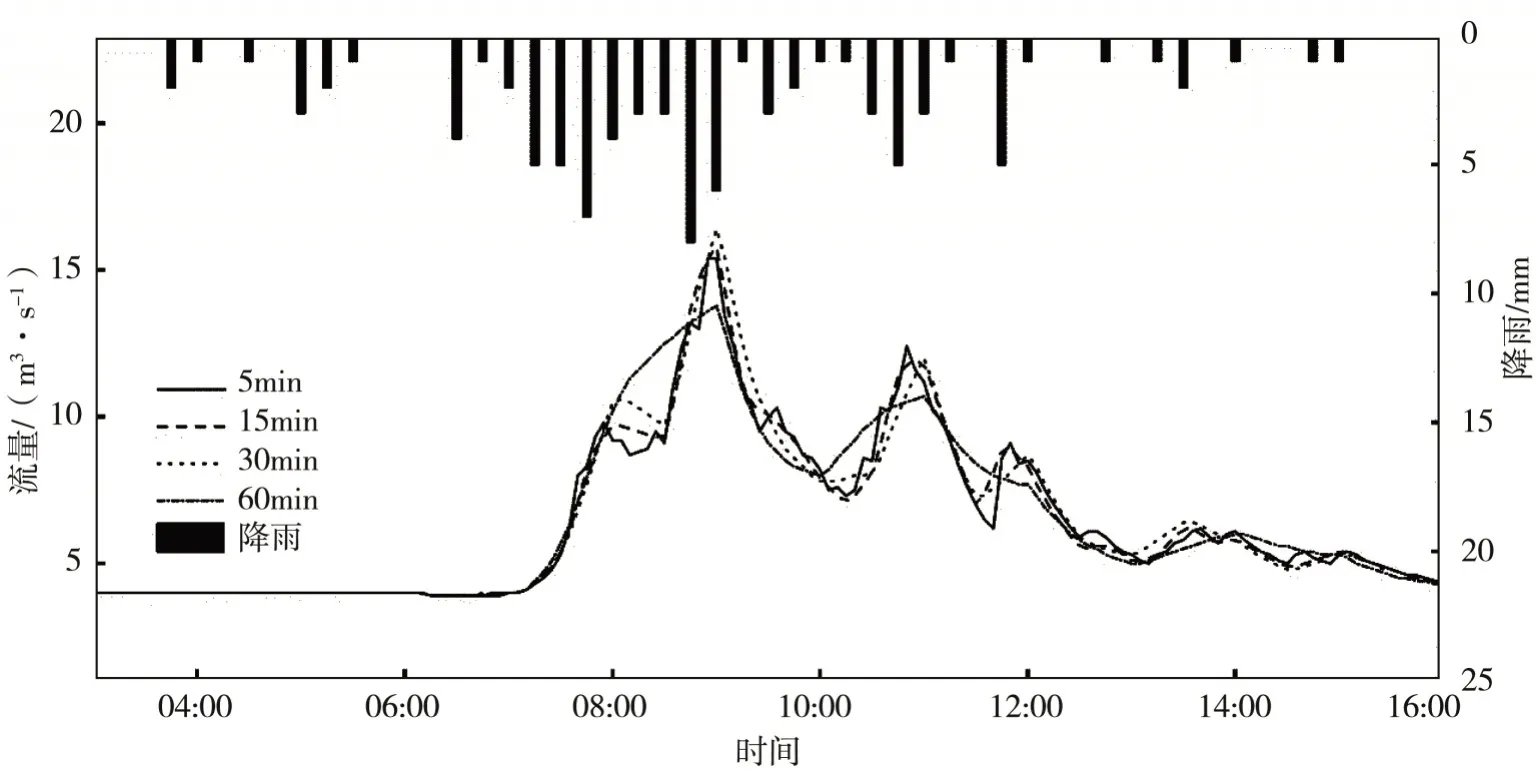
图12 不同时间步长下2015.6.22场次的径流过程对比Fig.12 Comparison of rainfall-runoff processes under different time steps on Jun.22，2015

（6）2014.8.21场次（图13）：该场次降雨较为复杂，不同时间步长的径流过程差异较大，第一次洪峰现时随步长增加而滞后，第二次洪峰峰现时间随步长增加而提前；时间步长为5～30 min时，峰现时差均比实测值提前，60 min步长的模拟峰现时间滞后10分钟；洪峰流量从17.0 m3/s递减至14.7 m3/s，洪水总量差异不大，误差保持在1%左右。

由此可知，时间步长的变化会对模拟过程线产生一定影响，尤其是60 min步长的模拟结果，虽也基本可模拟出峰值，但在洪峰流量和峰现时间等方面与5 min步长有较大差异。

（1）随着模拟时间步长的增加，峰现时间逐渐滞后，步长为5 min的峰现时差范围为-20～5 min，步长为15 min的峰现时差范围为-10～25 min，步长为30 min的峰现时差范围为-10～40 min，而步长为60 min的峰现时差范围为10～45 min。时间步长越精细，峰现时间的误差越小，反之会一定程度上推迟峰现时间。

（2）随着模拟时间步长的增加，洪峰流量总体趋势呈降低趋势，径流过程线趋于坦化，这是由于时间间隔的增加引起单位降雨强度的降低，削弱了洪峰流量。洪水总量的变化不大，这是由于虽然相对雨强降低，但总降雨量并未发生变化，因此，总产流量基本不变。

综上所述，初始雨量数据精度越高，时间步长越短，模拟效果越理想，即要求我们在进行洪峰模拟预报时，原始的雨量数据应尽可能的精确。但是在实际应用中，受限于环境条件，实际观测数据精度不够高，故应选择合适的时间步长进行径流计算。

5 结论与讨论

本文采用SCS产流模型和运动波方程，对震区一个小流域（2.4 km2）进行洪水模拟。从结果来看，对洪峰三要素包括洪水总量、峰值流量和峰现时间都能较好模拟。与实际监测资料相比，模拟的洪峰流量误差最大不超过5%，峰现时间误差在-20～20 min之间，洪水总量模拟误差在-22.79～14.27%，说明该方法可用于地震灾区小流域的水文计算。

在模型主要参数（CN和n）的确定过程中，首先根据经验值或查表值作为初始值，然后根据模拟结果进行调整，虽有一定的经验性，但历次降雨的CN最优值都在69～72范围内，因此相对合理且方便应用。模型对于长历时、多峰的复杂降雨中，在保障第一次峰值模拟精度的情况下，对后续洪水的峰值流量模拟效果较差。这是由于复杂降雨过程中峰值前的前期降雨造成流域产汇流条件发生改变，而模型并不能准确模拟该过程。

对于2 km2尺度的小流域，划分子流域的分布式模拟效果比将流域作为一个整体集总式模拟效果略好，但提升较为有限，考虑到西部山区流域参数获取的难度，分布式模拟可能造成参数输入的人为主观性，因此集总式模拟是可行的。降雨时段的控制和模拟时间步长对洪水过程模拟影响较大：在保持参数一致的情况下，随着时间步长的增加，模拟的峰现时间通常会滞后，且洪峰流量逐步偏小，径流过程线不断坦化。

实际监测资料是洪水等灾害发生机理研究和模拟计算的重要支撑，而目前由于自然环境恶劣、无传输信号、灾害频发、施工条件危险艰苦等诸多困难，在汶川地震灾区尚无一个小流域拥有丰富的监测资料。本文利用位于流域内部的降雨和径流数据，研究对象为震区一个具有数年监测历史的2 km2左右尺度的小流域，具有较高的代表性。但在推广应用时仍需考虑山区降雨的高度不均匀性和野外水文监测的复杂性，监测结果和研究结果仍具有一定的不确定性。