考虑围压影响的湖相软黏土K0固结经验蠕变模型
2022-03-10贺建清林孟源陈立国胡惠华陈秋南
贺建清,林孟源,陈立国,王 朦,胡惠华,陈秋南
(1.湖南科技大学岩土工程稳定控制与健康监测省重点实验室,湖南湘潭 411201;2.中南大学土木建筑学院,湖南长沙 410075;3.湖南省水利水电勘测设计研究总院,湖南长沙 410007;4.湖南省交通规划勘察设计院有限公司,湖南长沙 410200)
引言
软土广泛分布于沿海、河流滩涂及内陆湖泊地区,由于沉积环境特殊,矿物构成复杂,天然含水量高,多呈絮状结构,相较于一般粘性土,表现出明显的蠕变特性。随着工程建设对地基工后长期沉降控制的要求愈来愈严格,软土蠕变特性的研究日益受到重视。如何构建一个能准确反映软土蠕变性状的本构模型,并根据试验结果辨识模型、确定模型参数,使之能够用来准确预测工后软土地基的长期变形,成为软土蠕变特性研究的关键。
早期对软土蠕变模型的研究主要是利用常规固结仪进行[1-4],后来随着仪器研发水平的提高,通过三轴蠕变试验在蠕变模型的研究上取得了很多重要的研究成果[5-9]。描述软土蠕变特性的本构模型大致分为元件模型[10-14]和经验模型[15-17]两类。元件模型采用一些基本元件来表征软土的蠕变特性,如用“弹簧”模拟软土的弹性,用“粘壶”模拟软土的粘滞性,用“滑块”模拟软土的塑性,通过这些元件的组合-来反映软土的粘弹塑性特性。此类模型的概念直观、物理意义相对明确,但要准确描述土的黏弹塑性特性需要引入很多的元件进行组合,模型参数数量多,给工程应用带来不便。实际上,元件模型往往只能描述软土线性蠕变特征,对于具有非线性蠕变特征的软土,元件模型的适用性较差[18-19]。经验模型是根据软土的试验结果而抽象的应力-应变-时间关系,故其针对性较强,更能反映软土的蠕变特性[20-23]。目前,应用广泛的经验模型主要有Singh⁃Mitchell模型[24]和Mesri模型[25],多为根据等压固结单级加载的排水与不排水三轴压缩蠕变试验提出的应力-应变-时间关系模型。工程实际中,土体初始应力状态很大程度上决定着软土的力学特性,天然状态的结构性软土通常处于K0固结状态,显然K0固结各向异性的应力状态不可忽略。另外因为蠕变试验耗时很长,受时间限制,很多试验只做了一个围压下的三轴蠕变试验,提出的经验蠕变模型没考虑围压的影响,不具有普遍适用性。
软土分布地域特征明显,目前针对洞庭湖软土蠕变特性的研究相对较少。为了更加充分揭示工程实际中洞庭湖软土的蠕变特性,本文针对洞庭湖软土开展不同围压、不同应力加载等级下的K0固结三轴排水蠕变试验,分析洞庭湖软土的蠕变特征,建立适用于描述洞庭湖区软土蠕变特性的经验模型,为该地区工程的长期变形计算提供依据。
1 三轴蠕变实验
1.1 土样基本物理力学性质
试验用土样为淤泥质粉质粘土,取自长江右岸的黄盖湖流域江南垸的最北端、长江一线防洪大堤桩号K141+870~K142+050处的铁山咀泵站施工场地,取样深度10.7~12.1 m,其物理力学性质见表1。
1.2 试验设备及工作原理
试验设备采用GDS三轴试验系统,主要组成为加载系统、反力架、控制系统、测量及数据采集分析系统组成,能进行饱和土以及非饱和土的常规三轴试验,包括UU试验、CU试验、CD试验。当进行非饱和土三轴试验时,切换GDS试验系统测量相关数据。
1.3 加载方式及试验步骤
在蠕变试验方案设计中,常见的加载方式分级加载和分别加载两种,相比于实际蠕变过程,分别加载更符合实际工程中的蠕变情况,但在室内试验中,分别加载由于操作难度高,较为复杂,所需要的仪器较多。同时,分级加载也能较好的反映土体的蠕变特性,限于试验条件,结合分级加载的优势,本文所进行的蠕变试验采用分级加载的方式进行试验。
试验步骤如下:
(1)切取直径39.1 mm、高76 mm土样,装入饱和器,置于真空饱和缸内,抽气2 h后注水静止24 h,再装入采用GDS三轴试验系统中的压力室内施加110 kPa围压和100 kPa反压,反压饱和12 h后,使用B-Check模块加大围压30 kPa,观察B值,若其大于0.98,那么试样就达到了饱和状态,开始进入下一步试验,整个试验过程中反压保持不变,室内温度控制在20℃。
(2)利用GDS应力路径三轴试验系统进行K0固结试验,测定静止土压力系数K0,试验结果显示,洞庭湖淤泥质粉质粘土的K0值为0.44。
(3)试样在不同围压下完成K0固结,然后进行常规排水剪切试验,得到不同围压σ3(100 kPa、200 kPa、300 kPa、400 kPa)下的轴向破坏偏应力增量ΔSf(76.36 kPa、51.72 kPa、72.96 kPa、97.68 kPa),ΔS f=(σ1-σ3/K0)f。
(4)根据ΔSf确定蠕变试验每一级轴向荷载,共分为6级,每级荷载为η⋅Δq f,其中η分别取0.2、0.4、0.6、0.8、0.95、1.05,每一级轴向荷载维持7d且变形小于0.01 mm/h时进行下一级加载,三轴蠕变试验分级加载方案见表2。

表2 三轴蠕变试验分级加载方案Table 2 Graded loading scheme for triaxial creep test
2 蠕变实验结果分析
2.1 全过程轴向蠕变曲线
图1为不同围压σ3作用下K0固结、分级轴向加荷条件下全程轴向蠕变曲线。从其形态可看出,不同围压条件下的分级加载曲线趋势较一致。在较低偏应力条件下,试样轴向变形较小且变形时间较短,加载完成后变形很快能达到稳定状态,随下一级荷载的增加出现明显的瞬时变形,且随偏应力的增加,瞬时变形和蠕变变形的增长幅度明显增加。
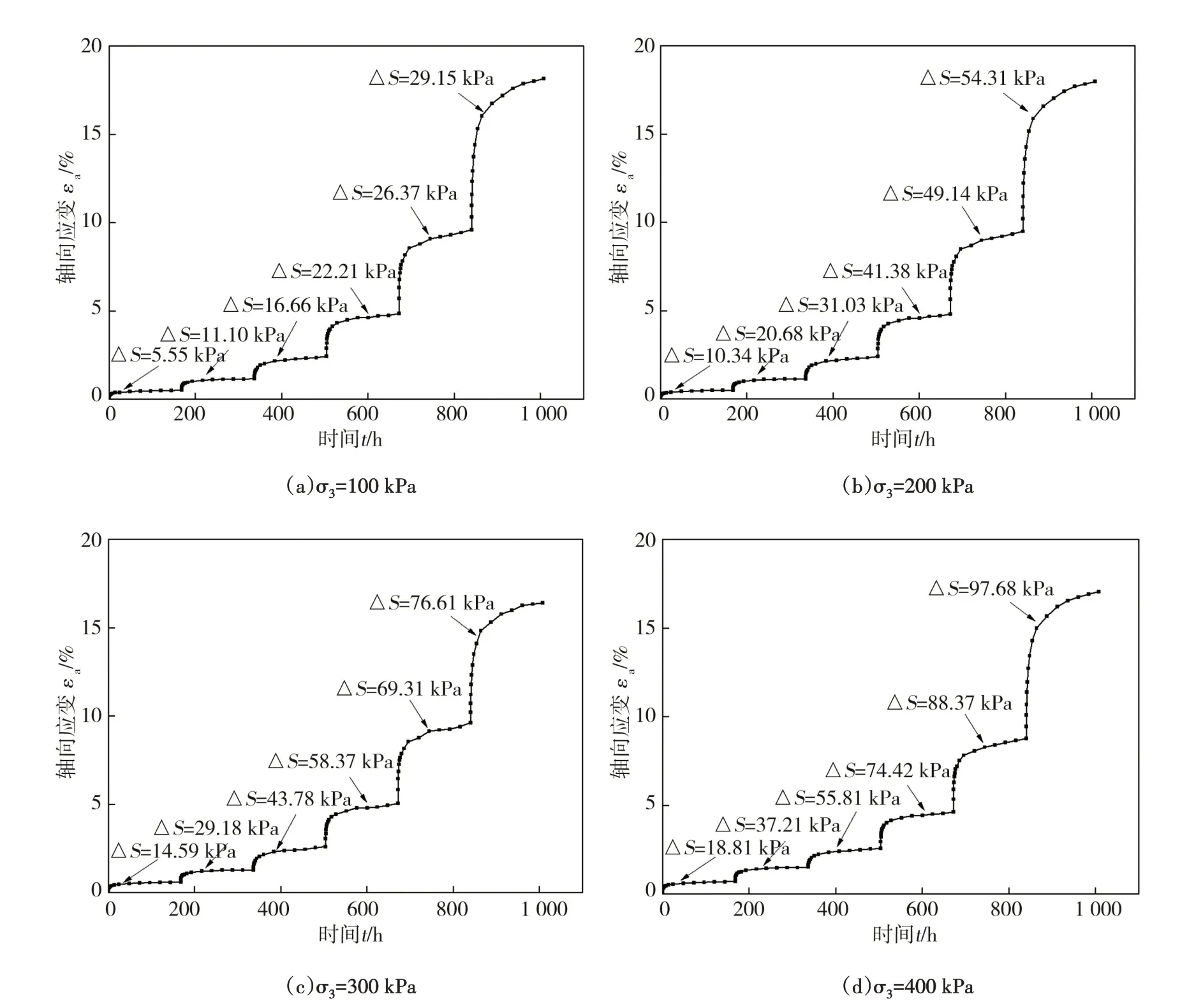
图1 分级轴向加荷下的全过程蠕变曲线Fig.1 Creep curve under graded axial loading
2.2 应力-应变等时曲线
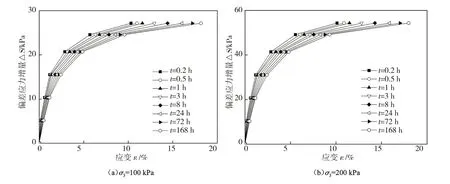
图2为试验得到的不同围压下的一簇相似的应力-应变等时曲线。时间不同,应力-应变关系曲线相异,在高应力条件下,应力-应变关系呈现明显的非线性特征,而且随着偏应力增量的增大愈加显著。对图2中等时曲线采用以下Kondner双曲线函数拟合

图2 分级轴向加荷下的应力-应变等时曲线Fig.2 Stress strain isochron curves under graded axial loading

式中:ΔS为偏差应力增量(kPa),ΔS=σ1-σ3/K0。式(1)中a、b值见表3。表3数据显示,与Mersi蠕变模型一致,用Kondner曲线来描述不同时刻洞庭湖软土的应力-应变关系比较合适。
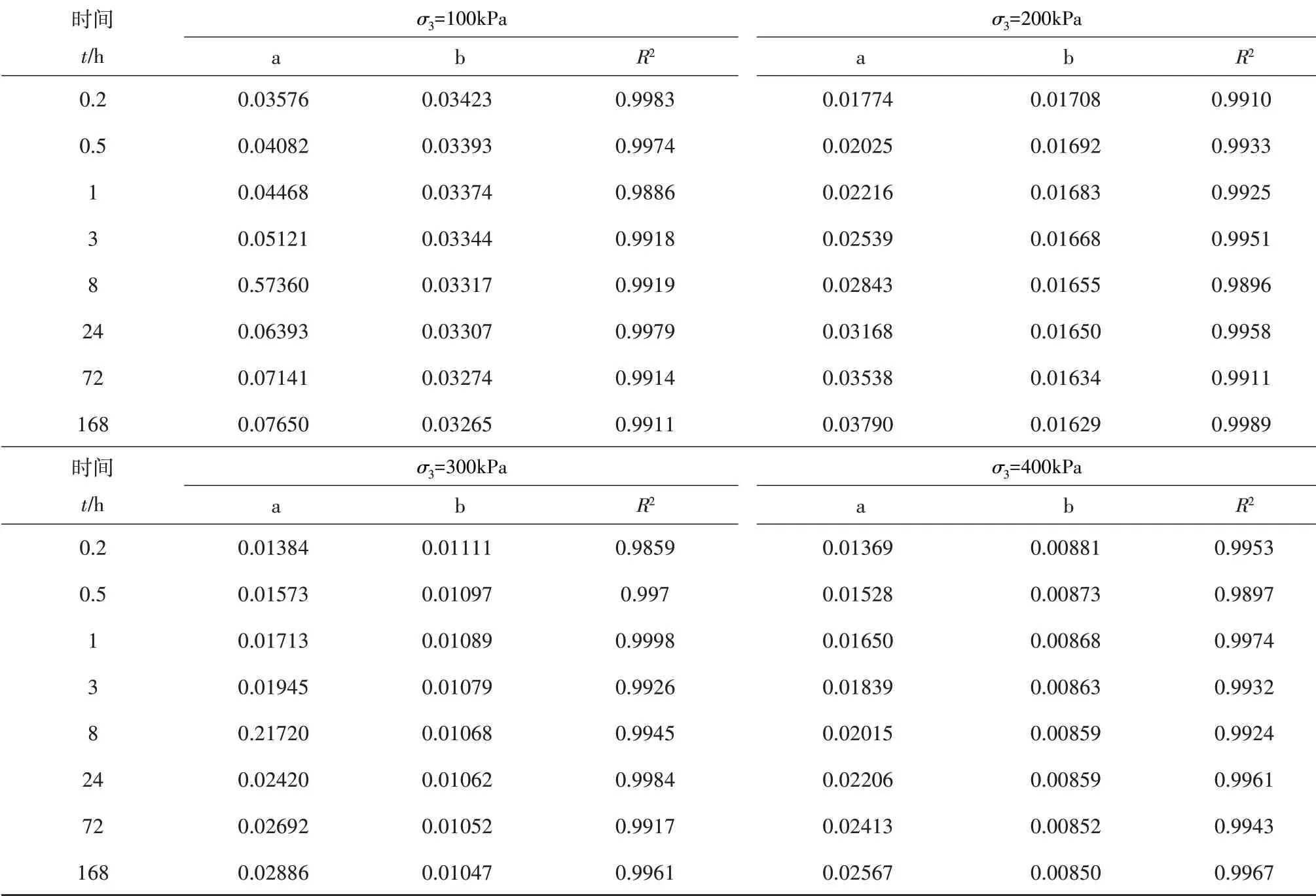
表3 a、b值Table 3 a、b value
2.3 轴向应变-时间关系曲线
图3为洞庭湖软土在不同围压、不同轴向荷载作用下软土变形随时间的变化曲线。图3显示,轴向应变ε与时间t在双对数坐标中呈良好的线性递增关系,并且在各级荷载作用下的lnε⁃lnt关系曲线几乎是相互平行的直线。
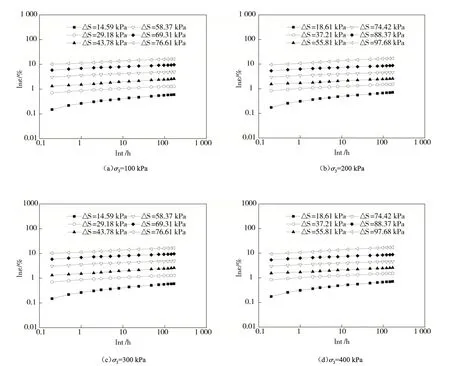
图3 ε⁃t双对数轴向蠕变曲线Fig.3 ε⁃t biaxial creep curve
3 经验蠕变模型
3.1 应力-应变-时间关系
在描述软土应力-应变-时间关系的经验模型中,最典型的是Singh&Mitchell于1968年提出的蠕变方程

式中:为应变率,S为剪应力水平;(σ1-σ3)f为等向固结三轴剪切试验过程中观测到的实际剪切破坏应力(kPa);t1为单位时间,α、m为常量参数。
m≠1,对式(3)积分可得

显然,在某一时刻t,式(4)描述的应力-应变关系呈指数型,且未反映土体的初始应力状态,与本文试验结果不符。将式(4)中的应力-应变关系由指数型改为双曲线型,并作归一化处理,得

式中:p为平均主应力(kPa)为归一化的双曲线拟合参数。

ε0=0,式(6)为

令t=t1

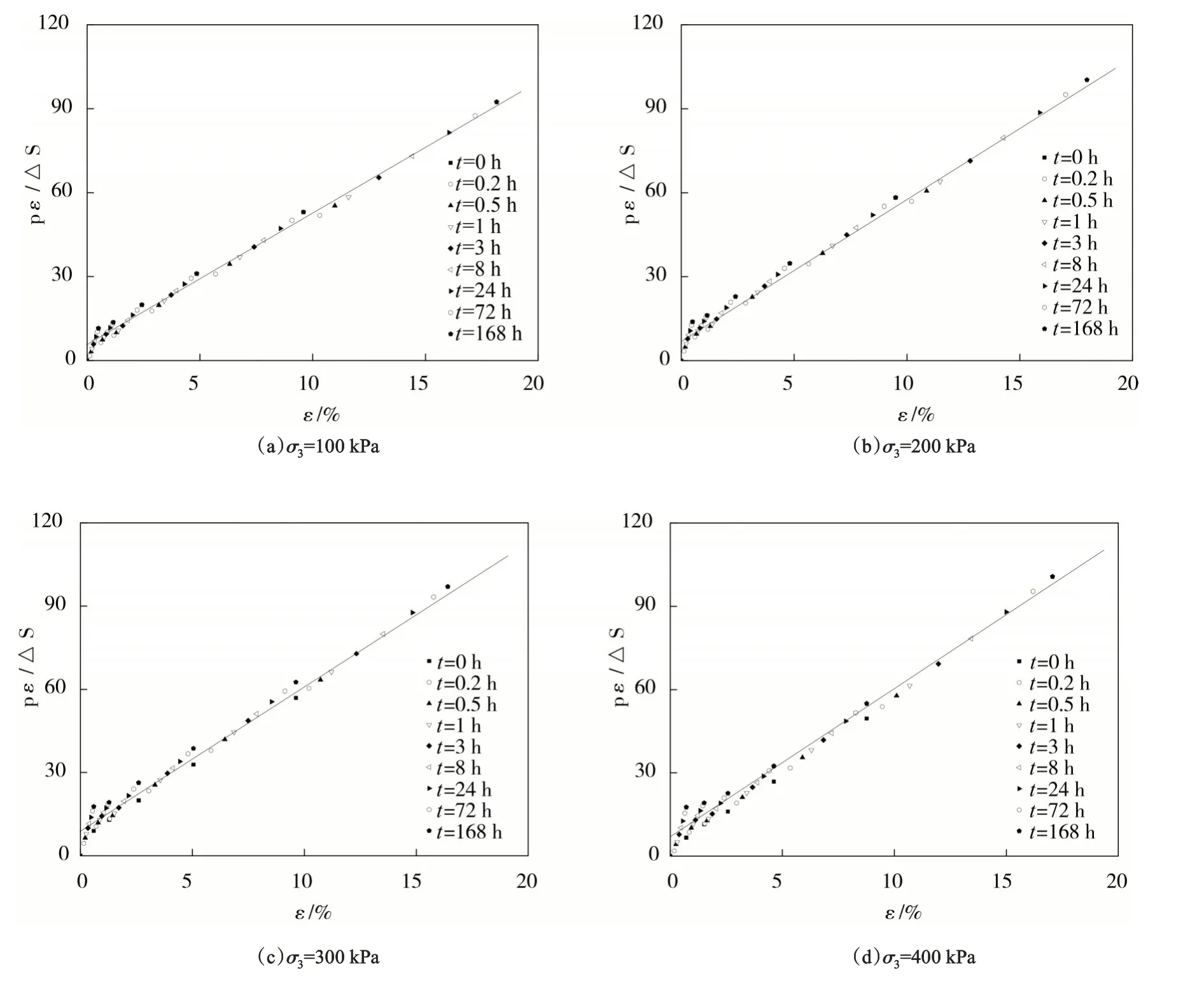
图4 归一化的应力-应变关系Fig.4 Normalized stress⁃strain relationship

表4 C、拟合值Table 4 C、fitting value
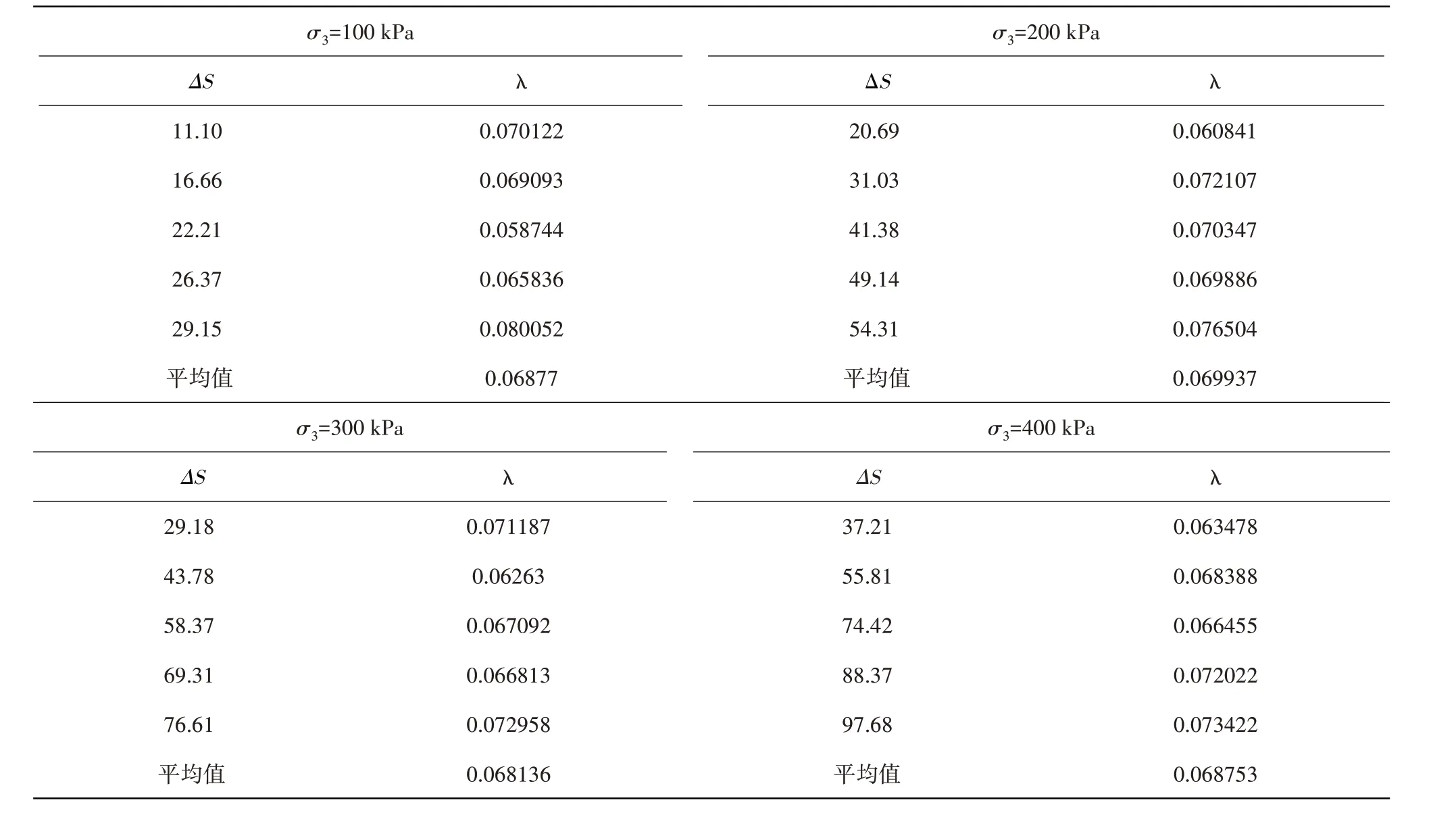
表5 λ值Table 5 λvalue
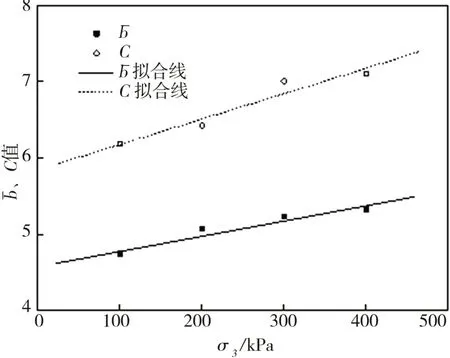
图5 C、与围压σ3的关系Fig.5 Relationship between Cand confining pressureσ3

式中:ξ、β、χ、ψ为拟合参数。
式(9)~式(10)中的洞庭湖软土拟合参数见表6。

表6 拟合参数Table 6 Fitting parameters
将式(9)、式(10)代入式(8)得

因参数λ为每级荷载作用1h后蠕变曲线的近似直线的斜率,可取t1=1h。根据试验确定的洞庭湖软土相关参数,建立洞庭湖饱和软土在排水固结条件下,不同围压、各级偏应力增量ΔS作用下的长期变形预测模型

3.2 模型验证
利用式(12)对软土沉降变形进行预测,并与固结试验的沉降随时间的变化数据进行对比(图6)发现,模型计算结果和试验结果较为一致,相关系数R2均在0.8以上,说明所建模型能较好地描述不同围压、不同应力水平下洞庭湖软土的应力-应变-时间关系,反映该模型适用性强。
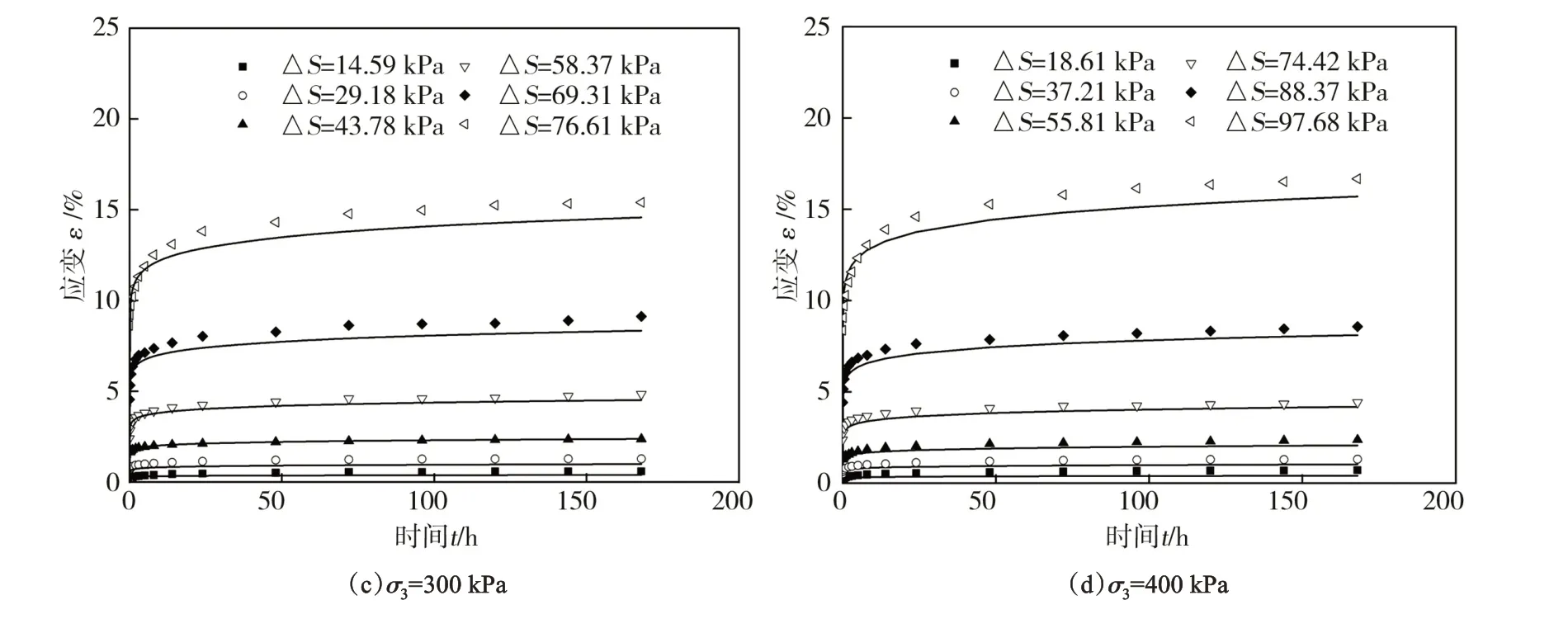
图6 试验数据与模型计算结果比较Fig.6 Comparison of test data and model calculation results

4 结论
采用分级加载法对洞庭湖软土进行三轴固结排水蠕变试验,基于试验结果构建洞庭湖软土经验蠕变模型,得到了如下结论:
(1)轴向应变ε与时间t在双对数坐标中呈良好的线性递增关系,并且在各级荷载作用下的lnε⁃lnt关系曲线几乎是相互平行的直线。
(2)洞庭湖区软土具有非线性蠕变特征,可采用双曲线函数来描述洞庭湖软土的应力应变关系,Singh-Mitchell模型适用于描述K0固结下洞庭湖区软土蠕变特性。
(3)发现Singh⁃Mitchell模型中的归一化双曲线拟合参数与围压呈线性递增关系,在此基础上建立了反映应力水平影响的5参数修正Singh⁃Mitchell模型。
