基于激光跟踪仪的工业机器人绝对定位精度提高方法＊

郑哲恩 龚婷 范晓骏

（上海飞机制造有限公司，上海 200120）

0.引言

工业机器人绝对定位精度，是指机器人执行作业任务时示教器的理论6D位姿与机器人工具点在空间中实际6D位姿的偏差，是衡量一台工业机器人在离线编程状态下能否精准、良好运行状态的重要指标[1]。

机器人运动学参数、动力学参数，以及环境参数均会对工业机器人的绝对定位精度指标造成影响[2]。其中，运动学参数[3]包含连杆长度、关节偏置、连杆扭角、关节转角。机器人零部件加工误差、整机装配、更换部件、长时间运转产生的机械磨损，减速器齿轮回程误差等因素均会造成机器人运动学参数理论与实际不符。机器人动力学参数包括关节刚度，内部零件摩擦，惯性，振动等因素[3]。其直观表现是末端负载变化或机器人工作速度变化引起机器人定位精度变动，环境参数误差主要由温度变化（热变形），电磁环境影响等因素引起[3]。

1.几何误差建模

在决定机器人绝对定位精度的所有误差源中，因几何参数理论与实际产生偏差而引起的定位误差占所有误差的80%以上[4]。由于大部分工业机器人的数学模型均采用D-H模型（运动学模型），综合考虑各误差源比重、误差参数的可辨识性以及相关精度校准方案的可行性，以几何误差参数作为误差模型主要参数而忽略其他次要因素，几何误差参数可由 Δai，Δαi，Δdi，Δθi表示。

（1）连杆长度参数误差Δai：工业机器人连杆因装配误差、运行磨损及机械加工误差等因素造成的偏差[4]。

（2）连杆扭角参数误差Δαi：工业机器人相邻连杆间由加工、装配引起的平行度、垂直度等形位公差偏差。

（3）关节偏置参数误差Δdi：工业机器人关节因装配间隙而产生的相邻关节之间的相对位置偏差。

（4）关节转角参数误差Δθi：工业机器人编码器误差，减速器齿轮加工、装配误差、机械校零时产生的零位偏移等因素引起的角度偏差。

根据D-H法则，机器人相邻连杆坐标系之间的转换关系可用齐次变换矩阵表示

由于D-H参数偏差，造成表示机器人相邻连杆坐标系之间的理论转换矩阵与实际转换矩阵不符，上述两个齐次变换矩阵的偏差记作，则有 ：

i-1连杆坐标系与i连杆坐标系因D-H参数偏差而造成的位置偏差为：

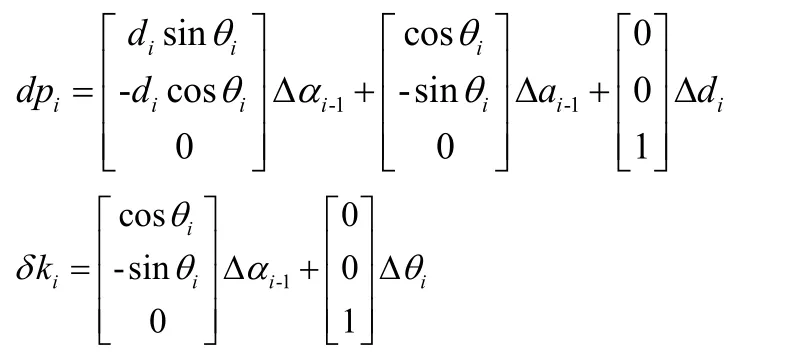
则可转化为

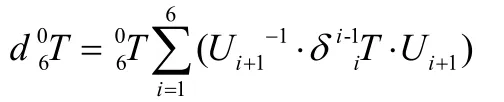
2.几何误差参数辨识

对于所有关节均为旋转关节的机器人而言，机器人运行不会改变连杆扭角，关节偏置，连杆长度这3个参数的值[5]。可直接利用激光跟踪仪通过圆周法测量分析得到上述3个参数，具体实现方式是：单独旋转机器人的6个关节，测量获取各个关节旋转轴线的法向，构造相应的几何特征，根据DH法则建立连杆坐标系，分析机器人各相邻连杆坐标系中X轴与Z轴之间的偏置与角度可初步确定a1～ a5，α1～ α5，d2～ d514 个参数。

将通过圆周法测量得到的参数作为初始值代入误差方程E=J·ΔK中，在测量获得多组机器人理论位姿与实际位姿偏差的条件下，利用迭代最小二乘法求解误差方程。通过递推算法可将方程f(x)=0改写成容易迭代的形式x=φ(x)，选择合适的初始值x0，代入φ(x)，计算得到的结果记为x1=φ(x0)，一般x1≠x0；把x1代入φ(x)，计算得到的结果记为x2=φ(x1)，若把xk代入φ(x)，一般有[5]：

xk+1=φ(xk)（k=0,1,2…）

由此得到迭代序列x0，x1，x2,…xk,…若迭代序列{xk}收敛到x＊，可得：

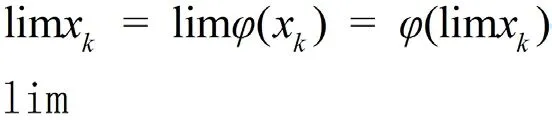
如果{xk}为发散则表示迭代不成功。

将误差方程E=J·ΔK转换成x=φ(x)的形式，由于J矩阵不能直接求逆，故采用的误差方程为[6]：

ΔK=(JT·J)-1JTE

将激光跟踪仪测量获取机器人位姿偏差与几何参数的初值代入误差方程中，求出参数误差的估计值，更新几何参数，重新代入误差方程中通过最小二乘法求出残差，循环上述过程，直到最终残差小于设定的阈值ξ时，停止迭代[6]。

3.位姿补偿实验研究

实验采用API的RADIAN激光跟踪仪配合末端执行器等相关辅助装置获取SR10C机器人的实际位姿。

测量姿态参数至少需要3个检测点，根据测量需求设计了可同时搭载3个靶球的末端执行器如图1所示。以靶球1中心为原点，3个靶球构成平面法向为Z方向（与法兰坐标系Z方向一致），X方向与机器人法兰坐标系一致，建立靶球坐标系。

图1 末端执行器

利用跟踪仪采集机器人立方体空间的8个顶点[6]，通过最佳拟合确定机器人的基坐标系。

在原始工具坐标系下，控制器显示的坐标数值是机器人法兰坐标系的位姿，而跟踪仪只能采集靶球坐标系的位姿，即需标定机器人工具坐标系获取靶球坐标系与法兰坐标系的转换关系。

本文提出一种基于激光跟踪仪的简便快捷的机器人工具坐标系标定方法（见图2），具体步骤如下：

图2 机器人工具坐标系标定

（1）操作机器人到空间中一固定点记为点TCP，激活初始工具坐标系，使机器人末端分别绕其坐标系的X,Y,Z轴旋转，并用跟踪仪测量靶球1的中心坐标。

（2）将激光跟踪仪测量的点拟合成一个球体，球心即为机器人法兰中心即法兰坐标系原点。

（3）操作机器人返回点TCP，激活初始工具坐标系使机器人沿X轴移动一小段距离后测量靶球1的位置，该位置与TCP的连线即为法兰坐标系的X轴，用类似的方法确定法兰坐标系的Z方向，已知法兰坐标系原点从而建立该坐标系。

（4）点TCP在法兰坐标系下的坐标为（-28.39，-0.73，186.68），该坐标即为当前工具坐标系中的位置参数，当前工具坐标系的姿态参数与初始工具坐标系保持一致。

在完成标定机器人基坐标系及工具坐标系的条件下，在机器人工作空间内均匀取50个位姿进行测量，分别记录示教器中的理论位姿和对应的跟踪仪实测位姿，通过圆周法与迭代最小二乘法结合的方法求出D-H参数的实际值如表1所示。

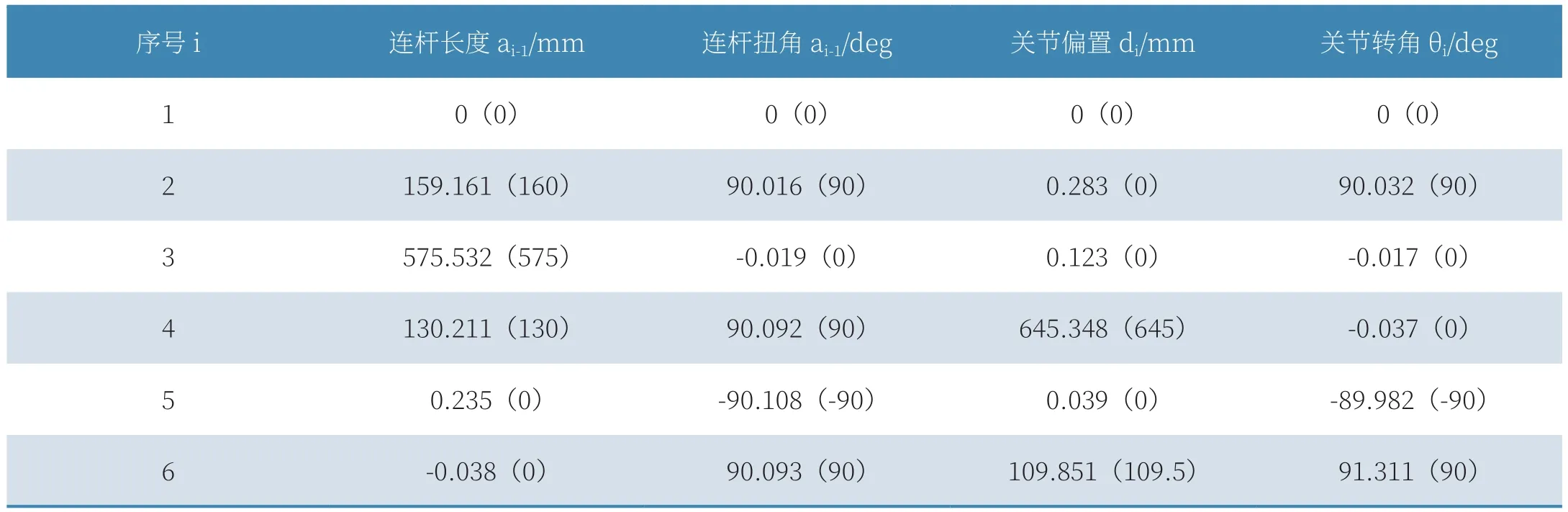
表1 D-H参数辨识结果

修改机器人控制器中相应的运动学参数，控制器重新计算50个测点的位姿。新松SR10C机器人的最大位置误差降低至补偿前误差：12.781mm的11.659%；平均位置误差降低至补偿前误差：7.683mm的12.2%；均方根位置误差降低至补偿前误差8.041mm的12.5%。在姿态误差方面，补偿后各欧拉角的均方误差相较于补偿前欧拉角RX均方根误差0.802°，RY均方根误差0.712°，RZ均方根误差0.811°也有了极大的改善，补偿前后的位置误差和姿态误差对比如图3所示。

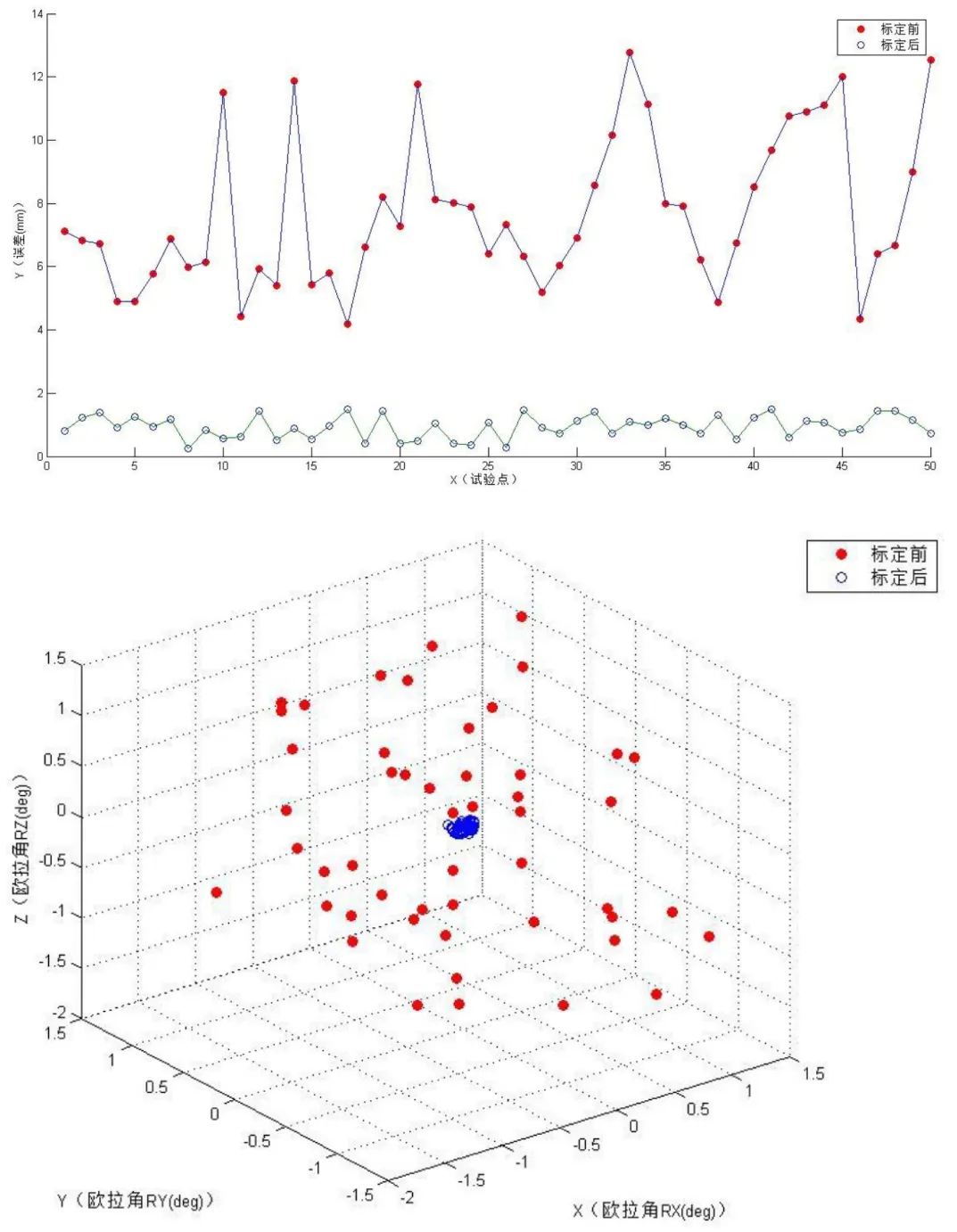
图3 补偿前后位置及姿态欧拉角误差对比

4.结语

本文以SR10C机器人为研究对象，结合工程理论和实际应用，探讨提高工业机器人绝对定位精度的方法，分析绝对定位误差的误差来源，在建立几何误差模型的基础上，采用圆周法与最小二乘法结合的方法获取机器人实际运动学参数，将其更新至机器人控制算法中，有效降低了该型机器人的绝对定位误差。